单词嵌入——自然语言的连续空间表示
陈恩红 邱思语 许 畅 田 飞 刘铁岩
(1.中国科学技术大学计算机科学与技术系,合肥,230027;2.南开大学计算机科学与信息安全系,天津,300071;3.微软亚洲研究院,北京,100080)
引 言
随着大数据时代的到来,海量的未标注的语料数据为文本处理的相关研究(诸如自然语言处理、信息检索、文档建模等)带来了新的机遇与挑战——一方面,大量的未标注文本中将为文本处理任务提供非常多的有用信息;另一方面,如何充分挖掘这些潜藏的有用信息,并将其应用于不同的文本处理任务等问题也随之而来。基于半监督学习的方法[1-3]可以部分利用这些无标记文本,并在特定的自然语言处理任务上有着良好的表现。但这些方法依赖于某一特殊的模型,其训练出的信息很难适用于其他的有监督任务。
为了解决这一问题,越来越多文本处理领域的研究人员开始专注于单词嵌入的方法。具体来说,单词的嵌入表示定义为每个单词关联的某种数学对象,通常来讲该数学对象是一个实数值向量。单词嵌入表示的目标在于学习到每个单词的向量表示,并将这种向量表示用于不同的文本处理任务。学习到的单词向量既可以作为完全的单词特征输入到某些特定任务的有监督学习算法中,也可以作为依赖于不同任务所特定提取特征的有益扩充。
为了将单词与实数向量关联起来,一个最简单的方法在于使用只有一位为1,其他位全为0的向量(One hot representation)。具体来说,假设词典为V,对于V中的第个单词,其关联的向量为wi=(0,0,…,1,0,…)∈{0,1}|V|,wi的第i位为1,其他位都为0。这种方法非常简单,但却有两个主要的缺点:(1)单词向量维度是词典大小,而词典中的单词数目往往很大,从而导致向量维度太大,引起计算上的不便;(2)该种表示唯一记录的是单词在词典中的索引,并没有刻画单词之间的相似度,从而没有为后续的文本处理任务带来更多的有用信息。
为了解决上述One hot表示方法的缺点,研究人员开始将注意力转到从大量的无标记文本语料中学习到更有效的单词嵌入表示。这里“有效”有两层含义,一是相对于词典大小,单词嵌入向量的维度非常低,可以认为每一维均对应某种语义的表示而没有冗余信息;二是对于类似的单词(比如′cat′和′dog′),它们的向量表示也相近。海量的文本语料无疑为实现这种有效性提供了很大的帮助:文本预料中包含的单词共现以及单词先后顺序等机构化信息提供了刻画单词相似度的来源,从而为学习到语义层面有效的单词嵌入表示带来了极大的方便。
1 主要方法简述
为了充分挖掘无标记语料中的信息以获取有效的单词嵌入表示,研究人员开发了多种新的机器学习方法,其中主要包括基于神经网络的方法、基于受限玻尔兹曼机的方法以及基于单词与上下文相关性的方法。
在基于神经网络的方法中[4-7],单词的嵌入表示常常作为神经网络的权重矩阵,神经网络通过优化某个目标函数更新其权重矩阵,从而学习到较优的单词嵌入表示。通常来讲,神经网络优化的目标函数是极大化文本语料的生成概率[4],或者是尽可能符合某种具体任务的标记信息,例如词性标注(Pos tagging)任务中的标注信息。
与基于神经网络的方法类似,基于受限玻尔兹曼机的方法[8]的目标同样是极大化文本语料的生成概率。二者区别在于具体模型的构建——在该方法中,受限玻尔兹曼机被用来建模文档的概率,单词嵌入向量作为受限玻尔兹曼机的参数。因为受限玻尔兹曼机的目标函数的梯度无法精确求得,其训练过程是近似的梯度下降,这也与训练传统的反向传播神经网络有很大的不同。
基于单词与上下文相关性的方法首先构建单词与上下文的共生矩阵,这里上下文可以是所有文档、每个单词的左窗口、右窗口等;然后对共生矩阵做矩阵分解,从而得到每个单词的低维表示。与以上两种方法不同,基于单词与上下文相关性的方法一般不是概率模型,其训练方法一般是矩阵分解。
2 基于神经网络的方法
2.1 神经网络概率语言模型
使用神经网络以及单词嵌入技术构建语言模型的思想首先由Yoshua Bengio等人在文献[4,5]中提出。为了叙述方便,用缩写神经网络概率语言模型(Neural network probabilistic language model,NNLM)来代表该模型,同时引入一些记号:以V来代表词典中的所有单词的集合,即词典;训练样本是一串单词序列w1,w2,…,wT,对于任意t∈{1,2,…,T},均有wt∈V;每个单词嵌入向量的维度为m,将所有单词嵌入向量的矩阵记为C∈R|V|×m,即V中的第i个单词被映射成C的第i行Ci∈Rm。

式中:第一层映射为矩阵C,将离散的单词映射成了连续的向量;第二层映射为函数g,g使用多层神经网络来建模。具体来说,有
其中yi是未经正则化的第i个单词概率的对数,按照式(2)计算
需要学习的参数是θ={a,b,d,U,W,C},a∈Rh,b∈R|V|,d∈Rh,U∈Rh×m,W∈Rh×(n-1)m,C∈R|V|×m,h为隐层节点个数。该式对应下述的3层神经网络:
(1)输入层:通过查找表C将 (wt-1,…,wt-n+1)映射到向量x,将词典中的第i个单词映射成向量Ci;
(2)隐层:通过tanh(d+Wx+UCi)函数将向量(x,C′i)映射到隐层h维向量;
(3)输出层:将隐层向量通过线性变换(a,b)输出到最后一层,并使用softmax函数将其转化成概率形式。

2.2 树状加速方法
上述神经网络概率语言模型提供了一种学习单词嵌入的方法,同时利用学到的单词嵌入矩阵C,该模型可以建立更好的语言模型。但是该方法存在计算复杂度过高的问题:注意到在式 (1)和(2)中,在计算给定前n-1 个单词(wt-1,…,wt-n+1)单词wt的条件概率时,每个词典中的单词i对应yi的值均需要计算;即在计算隐层变量tanh(d+Wx+UC′)时,共需要Θ(hm(n-1)+|V|hm)次操作。对于词典非常大的情况,例如|V|≈20 000,计算该条件概率无疑非常耗时。为了克服这一问题,Bengio等人在文献[6]中提出了一种利用树状层次结构加速这一计算的技术,这一技术现在已经被广泛应用在了各种神经网络概率语言模型的工作中[9-12]。
该技术的基本思想很直观:注意到在上一小节陈述的基本模型中,事实上,由式(1),每个单词(的条件概率)均由所有的单词来表示,即每个单词均由|V|位的信息来表示,这导致了计算一个单词的条件概率的复杂度是|V|阶的。考虑将表示一个单词的位数降低。可以采取一种层次结构:一个单词首先属于某个大类,自顶向下分别再属于某些子类,直至到达这个单词。以单词‘tiger’为例,它的层次类别可以如下:‘所有单词’→‘noun(名词)’→‘living things(生 物)’→ ‘animal(动 物)’→‘mammals(哺乳动物)’→‘cats(猫科动物)’→‘tiger(老虎)’,可见通过7个节点即可以表示单词‘tiger’,远远低于词典的大小|V|。
具体来讲,词典V中的每个单词v均关联一个二值的向量(b1(v),…,blv(v)),lv是v关联的向量的长度。该向量可以解释为lv个二值的决策,例如b1(v)=1代表单词v属于最顶层的类1,b1(v)=0代表单词v属于顶层的类2。为了得到每个单词的该二值向量表示,可以构建一棵叶子节点为所有单词的二叉树,对于每个单词,从二叉树的根节点到该单词对应的叶子节点的路径即是该单词对应的二值向量表示(例如,取转向左儿子为1,转向右儿子为0)。构建二叉树的方式,可以采用从知识库(例如 Wordnet)中学习到单词分类的方式[6],也可以采用按照语料中的单词分布构建的方式以加快运算速度[10],Mnih和 Hinton在文献[9]中对各种不同方式构建的二叉树的性能给出了实验性的总结。

其中sigmoid(x)=1/(1+exp(-x));βnode类比于(2)中单词的偏置项bi;α类比于式(2)中的a;d,W,U与(2)中对应的符号含义相同;类似矩阵F代表所有单词的嵌入向量,矩阵N给出了所有二叉树内部节点的嵌入向量。
使用这种树状加速方式,构建的二叉树很容易做到最长路径长度是O(ln|V|)阶,则计算一次条件概率的复杂度由O(|V|)降低到了O(ln|V|),极大提升了运算效率。
2.3 Word2Vec嵌入模型
在2012年和2013年,Thomas Mikolov等人在Google Research的工作单词向量表示(Word to vector,Word2Vec)[7,10]引起了学术界和工业界的广泛关注。Word2Vec模型计算简单,并且在一些有趣的任务上取得了很好的效果,比如寻找单词之间的线性关系(Tokyo-Japan+France=?)等。
Word2Vec同样属于神经网络语言模型,也采取了树状加速方式,但与经典的神经网络概率语言模型[4]相比,Word2Vec有以下显著不同:
(1)不是定义给定前n-1个单词的情况下出现第n个单词的概率,而是给定一个窗口大小(比如n),计算给定该窗口其他n-1个单词的条件下出现窗口中心的单词的概率;即此时考虑的上下文不再仅仅是左窗口(上文),而是包括左窗口(上文)和右窗口(下文)。
(2)关于上下文向量x的构建:在Bengio等人的工作中,上下文向量x是单词wt之前所有n-1个单词嵌入向量的拼接,从而有x∈R(n-1)×m,m是单词嵌入向量的维度;而 Word2Vec与此不同:Word2Vec采取两种模型,一是CBow模型,在该模型下,x是窗口中所有n-1个上下文单词嵌入向量的平均值;二是Skip-Gram模型,在该模型下,x是每个上下文单词的嵌入向量,对于每个预测的窗口中心词,一共训练n-1次。故而在Word2Vec中,x∈Rm。
(3)不再设置隐层,而是直接将输入的单词嵌入向量与内部节点嵌入向量作用输出条件概率。
(4)在构建二叉树的过程中,使用了哈夫曼编码,而不是类比之前工作中使用WordNet构建;这样做的好处是使得运算速度更快,这是因为哈夫曼编码保证了词频高的单词对应的路径短(lv小),从而在预测该高频单词时需要更新参数的二叉树内部节点个数少。
综上所述,在Word2Vec模型中,类比于式(3)的条件概率为
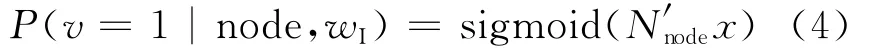
其中wI是上下文单词,x是wI嵌入向量,其他符号类似。
2.4 CW08嵌入模型
Collobert和 Weston等人在文献[12,13]中提出了一种可以解决不同自然语言处理问题的通用架构,为了叙述方便将这个架构简写为CW08。他们的贡献不在于解决了某个单一的自然语言处理问题,而是提出了一个对于多种自然语言处理问题通用的深层神经网络模型结构,使用这种网络结构可以生成一份通用的单词嵌入向量,来完成自然语言处理里面的各种任务,比如词性标注、命名实体识别、语句切分、语义角色标注等。
上述深层神经网络模型从逻辑上可以分为3个部分:单词嵌入层(查找表)、特征提取层和传统神经网络分类层。图1列出了这种网络结构。任务1和任务2共享同一个单词嵌入向量和卷几层。这种共享结构对于大于两个任务的情况也适用。
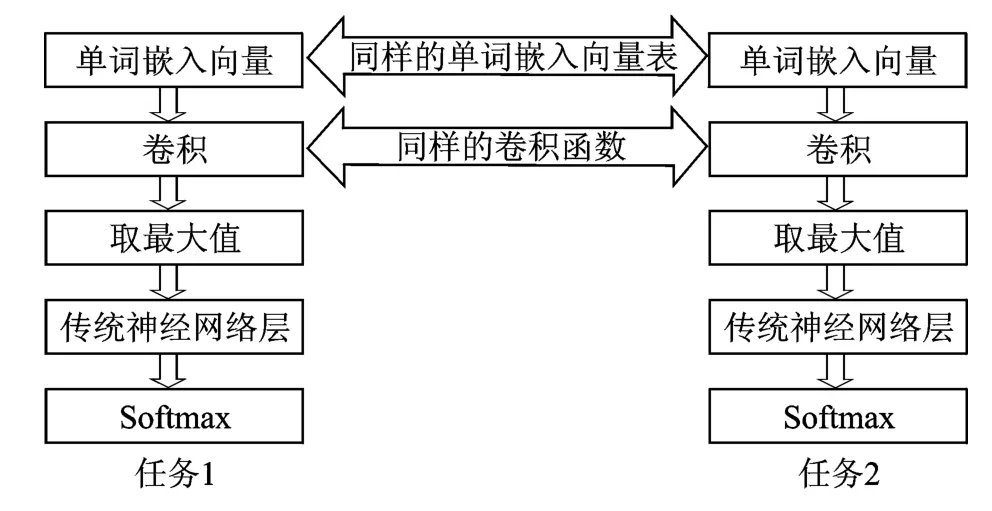
图1 一个多任务学习深层神经网络的例子Fig.1 An example of multi-task deep neural network
为了方便叙述,此处再次引入一些符号:L层前向传导神经网络记作f1(·),每一层神经网络记作,整个网络即为
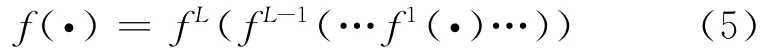
对于一个矩阵A∈,用Ai,j来表示其第i行j列的元素,用Aj来代表A的第j列。用来表示以A的第i列为中心的dwin列所拼成的列向量。即

这3层的结构和作用如下:
(1)单词嵌入层(查找表):给定一个单词序列(w1,…,wT),单词嵌入层的输出可以表示为
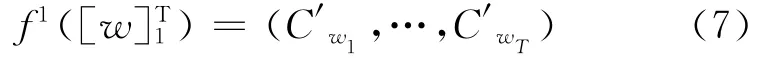
此处的参数C即是需要学习的单词嵌入矩阵,C的第i行代表词典中第i个单词的嵌入向量。
(2)特征提取层:这里跟卷积神经网络非常类似:输入是由T个连续单词嵌入向量构成的矩阵f1(上一层的输出),对每个宽度为dwin的连续单词窗口的嵌入向量表示,均使用同一个线性变换(W,b)将其映射到新的空间。此时该层输出的第个列向量(对应第t个单词窗口)可以表示为
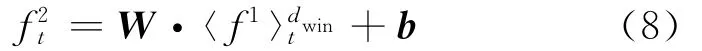
这里权重矩阵W和b偏置是要训练的参数。
对于所有的这些列向量,取出每一维的最大值,作为第三层的输出,即有
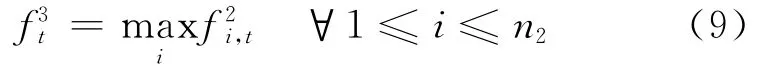
其中n2表示第二层节点的数量,即矩阵W的行数是n2。
(3)传统神经网络分类层:有了上面一层被降维且被提取了特征的向量,就可以用传统神经网络的方法解决上述自然语言处理问题,最常用的办法就是构造传统的神经网络分类器。
特殊地,对于语言模型问题,在该工作中没有建模条件概率P(wn|w1,…,wn-1),而是直接用神经网络最后的输出值作为联合概率分布P(w1,w2,…,wn)的估计,通过对n个词语序列打分来判断这几个词以某种次序出现在一起的合理性。对于随机替换中间词的得分应该比合理序列得分低。用数学方法表示为最小化
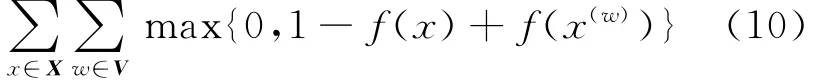
X表示所有输入文本窗口的集合,V表示字典集合,x(w)表示将窗口x的中心词随机替换成单词w所形成的新窗口。
接下来通过深度多任务学习就可以来训练整个网络。训练的目标是最小化所有任务的平均损失函数值。具体算法如下:
(1)选择下一个任务。
(2)为这个任务选一个随机的训练样本。
(3)用梯度下降算法来更新整个网络的参数。
(4)回到第一步。
至此得到了一份通过多个自然语言处理任务训练的单词嵌入表示。经试验证实,这种方法得到的单词嵌入表示在多种自然语言处理任务上都有比较好的表现。
2.5 递归神经网络语言模型
递归神经网络(Recurrent neural network,RNN)是一种特殊的前向传播神经网络结构。标准的RNN由3层构成:输入层、隐层和输出层,它的特别之处在于隐层通过一个重现矩阵和自己相连。重现矩阵可以传播延迟信号,从而使得RNN获得短期记忆的属性。具体来讲,RNN将上一个阶段隐层的信息保留下来,记作ht-1,在当前阶段,隐层的输出信息ht不仅仅与当前阶段输入wt有关,而且与上一阶段隐层记忆的信息ht-1有关。基于这两部分,隐层值ht得以更新,RNN模型也这种“递归”性质而得名。
具体到语言模型上,如果给定一串单词序列(w1,w2,…,wT),wt∈V。RNN 将利用式(11)计算相应的隐层序列(h1,h2,…,hT)和输出序列(y1,y2,…,yT)

图2递归神经网络语言模型总结了这种神经网络语言模型。这里wt代表第t个单词的onehot表示。需要学习的模型参数集合是θ={bh,by,W,U,A}。对于隐层激活函数的选取除了上述的双曲正切(tanh)函数,还可使用sigmoid函数。输出层可进一步使用softmax函数将线性输出转换为概率形式。最终学习到的矩阵W即是单词的嵌入矩阵。
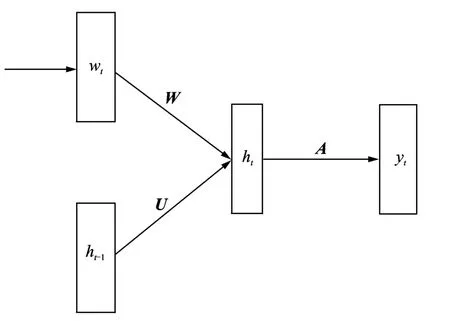
图2 递归神经网络语言模型Fig.2 Recurrent neural network language model
如此可见,在处理第t个单词wt时,RNN将前t-1个单词均考虑进来,而不是像经典的前向传播神经网络模型一样只考虑某个固定大小的窗口内的上下文单词(例如(wt-n+1,…,wt-1))。正因为这种不需要显式指定上下文长度的优点,RNN可以刻画更大范围的词间关系依赖。
虽然RNN的优点很明显,但是,当使用梯度下降法训练RNN却容易出现梯度爆炸和梯度消损的问题。梯度爆炸是指在训练的过程中错误信号在向后反馈时呈指数型增加的现象,梯度消损指的是相反方向,即错误信号以指数速率衰减为0。这两种现象是由长期信息爆炸式增加造成的。为了解决这两个问题,RNN模型在原有基础上又有许多扩展。Tomas Mikolov和Geoffrey Zweig提出了一个RNN的扩展模型[14](参见图3加入特征层的RNN模型):在原有的3层基础上加入特征层,与隐层和输出层相连。即,在当前词汇前,抽取一段固定长度的词汇,利用潜在狄利克雷分配[15]计算词汇的话题分布。一个近似的特征层输入可以写为
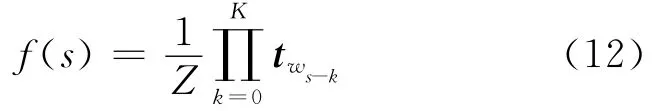
其中:twi是单词wi的LDA话题分布向量,Z使得结果归一化。在这样的模型下,单词的嵌入表示相应的变为
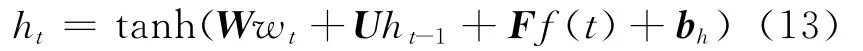
有了f(t)提供补充信息,长期的信息不会如之前一样以指数速率归一为0,从而避免了上文中梯度消损的问题。
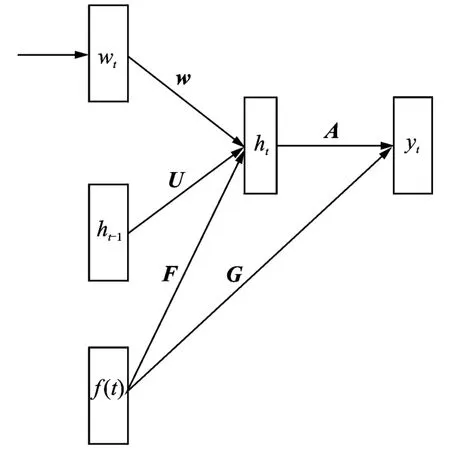
图3 加入特征层的RNN模型Fig.3 RNN model with feature representation layer
3 基于受限波尔兹曼机的方法
3.1 受限玻尔兹曼机
受限 玻 尔 兹 曼 机[16,17](Restricted Boltzmann machine,RBM)是机器学习界普遍采用的一种生成模型,它是一种无向概率图模型,也称为马尔科夫随机场。主要用来建模观测数据的生成概率,需要说明的是RBM处理的数据一般是离散的。
具体来说,给定dx维的观测向量x∈{0,1}dx,以及dh维的隐向量h∈{0,1}dh,RBM建立它们的联合概率分布
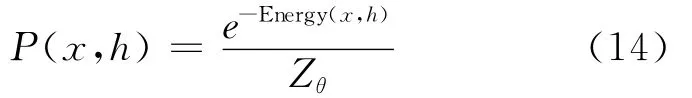
在以上的概率参数表达下,RBM的推断问题变得相对简单,数学上可以证明[16],对于RBM,有下式成立
其中W,i是矩阵W的第i列。这样,计算给定观测变量x的情况下隐变量的条件概率可以通过计算dh个条件概率得到,即给定x,对于任意的i,j∈{1,2,…,dh},i≠j,hi,hj是独立的。类似地,有
其中Wi,是矩阵W的第i行。训练RBM的过程即是极大化观测数据似然的过程。为此,求得在x0处的概率P(x0)=∑hP(x0,h)关于RBM 参数θ的梯度为[16]
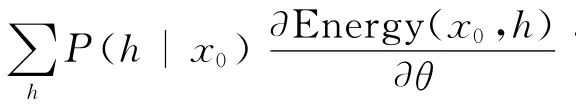
基于上述的RBM模型,Mnih和Hinton在文献[8]中提出了3种概率图模型来求得单词嵌入。3种模型的关键在于如何定义不同的、以单词嵌入向量为参数的能量函数。其中前两个模型包含了隐变量,与RBM的能量函数形式很相似,第三个模型(对数线性模型)没有隐变量。
3.2 两种隐变量模型

第二个模型——时序分解RBM模型采用了与递归神经网络类似的思想,注意到事实上单词wt之前所有的单词(w1,w2,…,wt-1)对wt均有影响,然而大部分工作都做了一个很强的假设:wt仅与其之前的n-1个单词(wt-n+1,…,wt-1)有关。时序RBM模型的目标就在于克服这种假设,即用给定的单词序列(w1,…,wt+n-1)预测单词wt+n。
为了达到这个目的,在预测单词wt+n时,对数线性模型维持了t个与分解RBM模型非常类似的模型,即t个n单词序列(w1,…,wn),(w2,…,wn+1),…,(wt,…,wt+n-1)中的每一个均作为一个独立的分解RBM模型的可见变量。这样得到了t个隐层表示,使用hτ来代表第τ个模型的隐层变量。
为了将上文中的信息不断后传至需要预测的单词wt+n,在第τ+1个模型中,除了第τ+1个n单词序列,上一个模型的隐变量hτ也作为第τ+1个模型的输入可见变量参与训练,hτ与hτ+1之间的交互矩阵A是多层之间共享的,即A不随着层数τ而改变。时序分解RBM模型通过这种“组合本层原有输入与上一层输出作为本层真正输入”的方式克服了之前n单词窗口方法的局限,不难看出该方式与递归神经网络的思想是非常类似的。
两个模型的推断和学习与经典的受限玻尔兹曼机推断和学习的方式类似,此处不再赘述。
3.3 对数线性模型
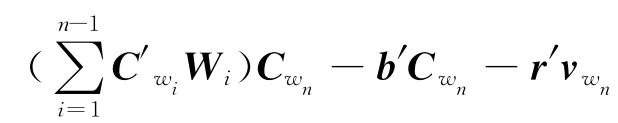
舍去隐变量使得模型的物理意义更清楚,同时使得计算更加简单。事实上,该模型与Word2Vec模型非常类似,除了以下两点不同:
(1)LBL对不同位置的单词指定了不同的参数矩阵Wi,而 Word2Vec中不存在这样的矩阵,Word2Vec直接使用上下文单词与预测单词的嵌入向量作用,即相当于W1=W2=…=Wn-1=I,I为单位矩阵。
(2)做预测时,Word2Vec考虑被预测单词的上下文,即左窗口和右窗口内的单词均考虑,HBL则仍是只考虑上文(左窗口)。
在文献[9]中,Mnin和Hinton采用上文所述的树状加速方法对对数线性模型进行加速,取得了良好的实验效果。他们不使用任何外部知识数据(例如WordNet)构建的单词树,而是采用一种基于训练语料的类似自助法的方式:首先构建一棵随机的单词树,然后基于该树训练得到单词嵌入向量,最后基于得到的单词嵌入向量进行层次聚类产生最终使用的单词树。
4 基于单词与上下文共生矩阵分解的方法
用F来代表单词与上下文的共生矩阵。一般来讲,是一种刻画单词与其上下文的一种计数模型,F的行空间是单词空间,列空间是上下文空间,F的行列元素Fi,j代表第i个单词和第j个上下文环境的关系,一般是单词i在环境j中出现的次数或者频率。构建了共生矩阵F之后,对F做矩阵分解,即可得到单词在隐空间上的一个表示,即为单词的嵌入向量。基于不同的上下文可以构建不同的矩阵。
4.1 潜在语义分析
潜在语义分析(Latent semantic analysis,LSA)[18]是一种分析单词与文档相关性的常用方法。在LSA中,上下文是所有的文档,假定词典大小为p,文档数为q,则F∈Rp×q,Fi,j代表第i个单词在第j个文档中频率,或者tf·idf值。LSA对F矩阵实施奇异值分解

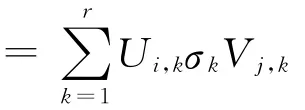
可见,可以使用矩阵U作为单词的嵌入向量矩阵,U的第i行即是单词的嵌入向量,该嵌入向量是r维的。
4.2 基于典型相关分析的方法
基于典型相关分析(Canonical correlation analysis,CCA)的方法[19,20]构建的上下文矩阵有两个:一是每个单词左窗口内的所有单词;二是每个单词右窗口内的所有单词。该方法的基本思想是极大化两个矩阵的协方差。
典型相关分析(CCA)和主成分分析(Principle component analysis,PCA)类似:给定一个矩阵,PCA计算一个投影方向,使得矩阵的行向量投影到该方向之后方差最大;CCA与此不同的是它处理两个矩阵:以本文的问题为例,假设语料中共有n个单词(w1,…,wn),词典大小为|V|,用W代表所有单词的矩阵。用L和R分别代表单词的左窗口矩阵和右窗口矩阵,L∈Rn×|V|h,R∈Rn×|V|h,这里h是指定的窗口大小。希望计算得到两个方向φl和φr,使得L在φl方向的投影与R在φr方向的投影的协方差最大,可以认为这两个方向保持了L和R中最“有用”的一维信息。该最大化目标可以用下式来表达

其中E代表经验期望。用Clr(Cll)代表L和R(L和L之间)之间的协方差矩阵,易知Clr=L′R,Cll=L′L。那么可证明上式的解〈φl,φr〉由下面的方程给出
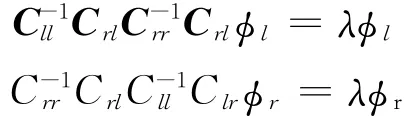
用〈φL,φR〉来代表m个最大的左特征向量和右特征向量集合,这里的“最大”指对应的特征值最大,可见φL∈R|V|h×m,φR∈R|V|h×m。基于上述符号,文献[20]中给出的两步典型相关分析算法如下:
(1)输入:矩阵L,W,R。
(2)对L和R做典型相关分析,CCA(L,R)→(φL,φR)。
(3)计算矩阵S=[LφLRφR]。
(4)对矩阵S和W做典型相关分析,CCA(S,W)→(φs,φw)。
(5)输出:矩阵φw,即为最终的单词嵌入矩阵。
该算法中,第一步是求左右窗口矩阵L,R的CCA,在求得后〈φL,φR〉,分别将L投影到φL方向,将R投影到φR方向(算法第三行),得到每个单词的一个隐状态S,S记录了左右窗口矩阵中最相关的m个成分。在第二步中,对矩阵S和原始矩阵W做CCA,以求得的m个关于W的投影矩阵φw∈R|V|×m作为最终的的单词嵌入矩阵。事实上,可以证明,第二步中求单词嵌入矩阵的过程就是对隐变量矩阵取平均的过程,有φw(w)=avg(St:wt=W)。
5 模型比较
各种方法的数学模型和实现细节的比较结果总结在表1。具体来说,比较的方面包括:(1)方法属于的类型,包括神经网络模型、受限玻尔兹曼机模型和共生矩阵分解模型。(2)训练的目标,包括极大化数据条件似然(maxP(wt|contest)、极大化数据观测似然(maxP(wt,context))、区分正确数据和错误数据(使观测数据的得分大于随机生成的错误数据得分)以及基于相关性的降维。(3)是否含有隐层。(4)模型考虑的上下文:包括窗口大小(固定大小、可变大小)、窗口位置(左窗口、右窗口)、单词所在句子以及所有文档;可变大小的窗口和左右窗口代表更多的信息被考虑进去,从而使得模型有更好的性能。(4)是否有加速方法。这里主要指树状加速方法。
各个方法的优缺点总结在表2。主要从3个
方面比较它们的优缺点:模型的表达能力强弱、训练效率高低以及优化的方法有没有理论保证(即可达到最优解)。
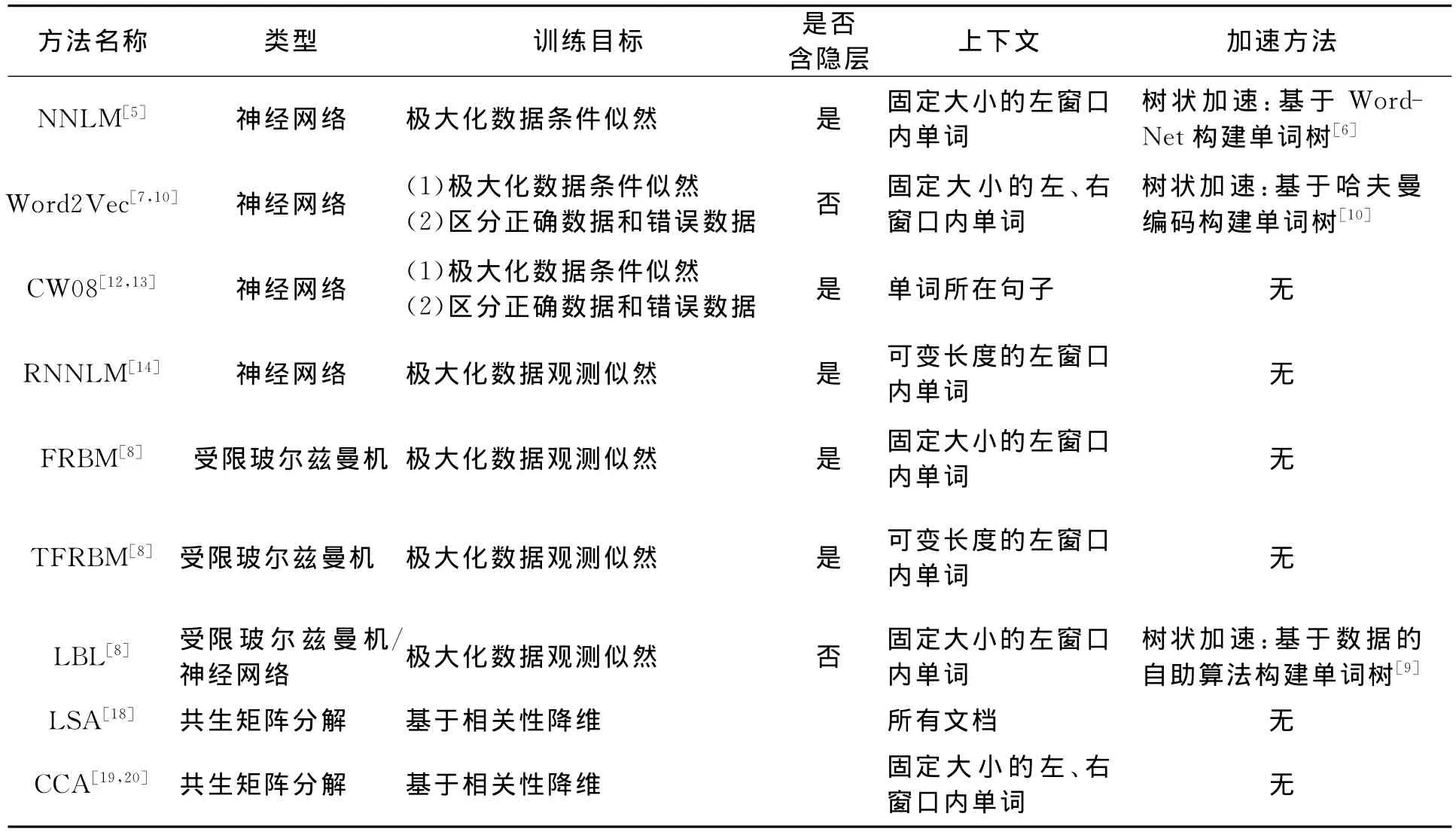
表1 不同单词嵌入方法的模型细节比较Table 1 Comparison of different word embedding models

表2 不同单词嵌入方法的优缺点比较Table 2 Pros and Cons of different word embedding models
表2中,几个缩写词的意义如下:RNNLM(Recurrent neural network language model,递归神经网络语言模型);FRBM(Factored RBM,受限玻尔兹曼机),TFRBM(Temporal factored RBM,时序分解受限玻尔兹曼机),其他缩写词全称已在文中全出。
6 结束语
单词嵌入是当今非常流行的用于文本处理任务的一种技术。本文综述了当下流行的各种求取单词嵌入向量的方法,包括基于神经网络的方法、基于受限玻尔兹曼机的方法以及基于单词与上下文共生矩阵分解的方法。本文阐述了各个方法的具体数学模型和实现细节,同时给出了各个方法优缺点的比较,以期让相关研究者更加熟悉单词嵌入这一技术,并将该技术应用到各种新的文本处理问题中。未来的单词嵌入向量工作中,一个重要的方向将外部知识库中的知识考虑进来,结合当前深度神经网络技术的飞速发展,产生更好的单词嵌入表示。这里的知识库可以包含单词形态相似度、句法相似度以及语义相似度等方面的知识,通过这样一些外部知识的辅助,深度神经网络将会得到对文本处理任务更有用的信息,从而有可能获得更好的单词嵌入表示。
[1]Rie Kubota Ando,Tong Zhang.A high-performance semi-supervised learning method for text chunking[C]//Proceedings of the 43rd Annual Meeting on Association for Computational Linguistics (ACL′05).Stroudsburg,PA,USA:Association for Computational Linguistics,2005:1-9.
[2]Suzuki J,Isozaki H.Semi-supervised sequential labeling and segmentation using giga-word scale unlabeled data[C]//Proceedings of the 46th Annual Meeting on Association for Computational Linguistics (ACL′08).Columbus,Ohio,USA:Association for Computational Linguistics,2008:665-673.
[3]Suzuki J,Isozaki H,Carreras X,et al.An empirical study of semi-supervised structured conditional models for dependency parsing[C]//Proceedings of the 2009Conference on Empirical Methods in Natural Language Processing:Volume 2.[S.l.]:Association for Computational Linguistics,2009:551-560.
[4]Bengio Y,Ducharme R,Vincent P.A neural probabilistic language model[C]//Advances in Neural Information Processing Systems.Vancouver,British Columbia,Canada:Neural Information Processing Systems Foundation,2001:933-938.
[5]Bengio Y,Ducharme R,Vincent P,et al.A Neural Probabilistic Language Model[J].Journal of Machine Learning Research,2003,3:1137-1155.
[6]Morin F,Bengio Y.Hierarchical probabilistic neural network language model[C]//Proceedings of the 10th International Workshop on Artificial Intelligence and Statistics.Barbados:ACM,2005:246-252.
[7]Mikolov T,Chen K,Corrado G,et al.Efficient estimation of word representations in vector space[EB/OL].arXiv preprint arXiv,2013:1301:3781.
[8]Mnih A,Hinton G.Three new graphical models for statistical language modelling[C]//Proceedings of the 24th International Conference on Machine Learning.Corvallis,USA:ACM,2007:641-648.
[9]Mnih A,Hinton G E.A scalable hierarchical distributed language model[C]//Advances in Neural Information Processing Systems.Vancouver,B C,Canada:Neural Information Processing Systems Foundation,2008:1081-1088.
[10]Mikolov T,Sutskever I,Chen K,et al.Distributed representations of words and phrases and their compositionality[C]//Advances in Neural Information Processing Systems.Nevada,United States:Neural Information Processing Systems Foundation,2013:3111-3119.
[11]Larochelle H,Lauly S.A neural autoregressive topic model[C]//Advances in Neural Information Processing Systems.Nevada,United States:Neural Information Processing Systems Foundation,2012:2717-2725.
[12]Collobert R,Weston J.A unified architecture for natural language processing:Deep neural networks with multitask learning[C]//Proceedings of the 25th International Conference on Machine Learning.Helsinki,Finland:ACM,2008:160-167.
[13]Ronan Collobert,Jason Weston,Léon Bottouet,et al.Natural language processing (almost)from Scratch[J].J Mach Learn Res,2011,12:2493-2537.
[14]Mikolov T,Zweig G.Context dependent recurrent neural network language model[C]//Proceedings of the 4th IEEE Workshop on Spoken Language Technology.Florida,United States:IEEE,2012:234-239.
[15]Blei D M,Ng A Y,Jordan M I.Latent dirichlet allocation[J].The Journal of Machine Learning Research,2003,3:993-1022.
[16]Bengio Y.Learning deep architectures for AI[J].Foundations and Trends in Machine Learning,2009,2(1):1-127.
[17]Hinton G E,Salakhutdinov R R.Reducing the dimensionality of data with neural networks[J].Science,2006,313(5786):504-507.
[18]Dumais S T,Furnas G W,Landauer T K,et al.U-sing latent semantic analysis to improve access to textual information[C]//Proceedings of the SIGCHI Conference on Human Factors in Computing Systems.[S.l.]:ACM,988:281-285.
[19]Dhillon P S,Foster D P,Ungar L H.Multi-View learning of word embeddings via CCA[C]//Advances in Neural Information Processing Systems.Granada,Spain:Neural Information Processing Systems Foundation,2011,24:199-207.
[20]Dhillon P,Rodu J,Foster D,et al.Two step CCA:A new spectral method for estimating vector models of words[EB/OL].arXiv preprint arXiv,2012:1206.6403.

