微积分中几个著名病态函数的理解与分析

周高军， 郑宝杰

(河南教育学院 数学与统计学院，河南 郑州 450046)

微积分中几个著名病态函数的理解与分析

周高军， 郑宝杰

(河南教育学院 数学与统计学院，河南 郑州 450046)

简要介绍了微积分中4个著名病态函数的历史及其重要性质.对这些函数的了解，一方面可以认识到病态函数在微积分的发展过程中所起的重要作用，另一方面还可以进一步增强对微积分中某些重要概念及结论的理解.

病态函数;Dirichlet 函数;Cauchy 函数;Riemann 函数; Weierstrass 函数

病态函数是指在某一方面表现出奇特性质的函数.因为它们具有其他函数不具备的性质,故经常用来作为反例.无论是在微积分理论本身的发展过程中,还是在微积分的教学中，病态函数都起着重要的作用[1- 2].本文介绍微积分中4个著名的病态函数:Dirichlet函数,Cauchy函数,Riemann函数和Weierstrass 函数.这些函数在微积分的发展历史中曾起过重要的作用，直到今天,其中一些函数无论在理论还是在实际中仍然有重要的应用.

1 Dirichlet 函数

函数是微积分研究的基本对象,它的定义看似平淡无奇,但事实上,从其起源到成熟,经历了一个漫长的过程.在 17 世纪的 Newton和 Leibniz 时代,微积分研究的主要是几何曲线(应该和Euclid所产生的深远影响有关),而且Leibniz 首先使用函数这个名词描述曲线的一个相关量.到了18世纪, Euler使人们把注意力从曲线转移到函数. Euler 首先区分了常量与变量，并给出了函数的定义:变量的函数是由变量与常量以任何方式构成的解析表达式.这些思想对于曲线来说是一种巨大的进步,但其定义需要通过解析表达式,即公式表示函数. 这一定义使得我们现代所接触到的一些函数不能被称为函数.再后来,Euler对函数的定义作了改进，如果某些量以如下方式依赖另一些量：当后者变化时,前者也发生变化,则称前一些量是后一些量的函数.

19 世纪初, Fourier在研究弦振动和热扩散问题时把函数的 Euler 定义进行了扩展,指出函数可以在定义域任意取值.但若要理解一个真正“任意”函数的概念,那么必须有人给出一个这样的函数,Dirichlet 函数就出现在此背景下.因此可以说,该函数的出现,是函数概念正式形成的标志,它的定义如下,

(1)

其中c和d是两个不相等的实数(最常见的情况是c=1,d=0,这时它是有理数集的特征函数[3]).

Dirichlet 函数有一些重要的性质,例如不能画出该函数的图像;它是周期函数,却没有最小正周期;它在实数集上处处有定义,但处处不连续;可以用它来构造本身非 Riemann可积但其绝对值函数却可积的例子.这些奇特性质以及由其构造的一些反例对积分理论的发展曾起着重要的促进作用[1].

2 Cauchy函数

在微积分的发展初期,即18 世纪,还没有严格的极限理论.虽然当时许多杰出的数学家如Euler等用微积分这一全新的工具解决了许多在过去被认为是高不可攀的难题,但同样也发现了一些解释不清的矛盾(这称为第二次数学危机[1]).许多数学家试图解决上述矛盾并建立微积分严格的基础,其中Lagrange曾提出一种方案,用函数的无穷级数(幂级数)来定义导数(这与现代的观点恰好相反),从而把无穷级数作为微积分的基础.但是,Lagrange的这一想法最终被证明是不可行的,因为Cauchy在1822年给出了一个反例,即如下定义的函数,

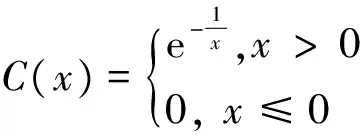
(2)

Cauchy函数C(x)有一个奇特的性质,它在x=0处可以展开为幂级数,但这个幂级数却不是收敛到C(x) (具体讨论见文献[4]).这也就是说,如果我们从函数C(x)开始,将它写成级数的形式,最终却得到一个完全不同于开始的函数,因而Lagrange的设想也就不是普遍有效,因而不能实现.当然,现在我们都知道,微积分的基础是建立在Cauchy所提出的严格的极限理论之上的(这一定义后来被Weierstrass符号化).

那么有人可能要问,在什么条件下,一个函数在某点的幂级数一定收敛到这个函数本身呢?答案是该函数在这个点是实解析的(具体讨论见文献[5]).反过来也就是说,Cauchy函数在0点不是实解析的.

3 Riemann函数

前文已指出,Cauchy提出了极限的严格定义,这是他对微积分的重要贡献之一.不但如此,他还以此为出发点,用极限给出了微积分中的其他重要概念如连续函数、导数以及积分的定义,这在微积分的发展过程中是具有划时代意义的.特别是积分的定义,在 Cauchy之前,积分一直被认为是微分的逆运算而在微积分的概念中处于次要位置.Cauchy是第一个把积分作为一个独立的概念并用分割区间的方法来定义的人.他的定义使得在两个关键问题上再无悬念:积分是一种极限,积分的存在同微分无关.

然而，应该指出，Cauchy关于积分的定义远非完美,因为他的定义仅适用于连续函数或至多有有限多个不连续点的函数.对这一定义进行推广的是 Riemann.他仅假定函数在某一闭区间上是有界的,对这样的函数提出了他的积分定义，并给出了一个函数在该定义下可积的充分必要条件.因为事先关于函数的连续性没有做任何假设,因此暗示着某些奇特的函数,比如非常不连续的函数也许是可积的(在他的定义下).Riemann确实给出了这样一个函数,其定义如下,

(3)

其中(x)表示实数x与和它距离最近的整数n之差,即(x)=x-n.

可以证明,函数R(x)在任意有限的区间内具有无限多不连续点,因而可以说是“高度不连续”的.然而,同样可以证明,该函数在闭区间[0,1]上是Riemann可积的[1].这就说明,Riemann关于积分的定义,确实比Cauchy的定义适用性更广,是它的推广.

另外,这个病态函数的出现还引发了另一个问题,即一个函数为了Riemann可积,可以不连续到何种程度?对这一问题的探讨持续了一个多世纪,到了20世纪初,才由Lebesgue给出了完美而且简洁的答案:一个在闭区间[a,b]上有界的函数f(x)在[a,b]上Riemann可积的充分必要条件是f(x)在[a,b]上几乎处处连续[3].

4 Weierstrass函数

我们知道,一个可微的函数必定是连续的,人们曾经认为连续函数必定存在可导点,而且除了某些孤立的点外,其余都是可微的,例如大名鼎鼎的Ampère还曾经“证明”过这样的结论.事实上，在 19 世纪前半期,微积分的教科书都支持这种见解[1].然而,Weierstrass函数的出现完全扭转了这一局势.该函数发表于1860年前后,其定义如下,

(4)

其中a≥3是一个奇数,b是严格介于0与1之间的一个常数且满足ab>1+1.5π.这个看起来奇怪的函数有一个更为奇怪的性质:它在整个实数集上处处连续,但处处不可微[1].

可以想象,Weierstrass函数的出现在当时引起多么大的震惊.它的出现,把几何直观作为微积分可靠基础的主张逐出了历史舞台.正如文献[1]中所指出的,分析学的严格性因Cauchy而提高,又因Weierstrass而达到一个新的顶峰.

当然,处处连续但处处不可导的函数远不止Weierstrass函数一个(但它却是第一个,也是最著名的一个).1930年,Van der Waerden给出了另一个(较为简单)例子[4].另外,1918年,Wiener给出了Brown运动的数学理论,结果表明Brown运动的样本轨道就是处处连续但处处不可微的函数[6].

也许有人会问,这些性质奇特的函数除了给出一个反例外,是否还有别的应用?答案是肯定的.因为20世纪末的数学家们发现,Brown运动可以用来刻画期权的价格波动(这一发现于1997年获得了诺贝尔经济学奖).粗略地说,期权的价格是随时间变化的函数,就是处处连续又处处不可微的.

5 小结

本文介绍了几个在微积分的发展历史中较为著名的病态函数.称这些函数为病态函数,固然是因为这些函数在某一方面具有一些奇特的性质,但重要的是还和人们的认识水平有关.因为对一些奇特性质难以解释或找不到直观背景等原因而称之为病态，而称其为病态也只是相对的,随着科学技术的发展,以及人们所处理问题的日益复杂,一些原来看似病态的函数,现在看来却是性质良好的,并且还发挥着重要的作用.

[1] WILLIAM D. The calculus gallery: Masterpieces from Newton to Lebesgue[M]. New Jersey: Princeton University Press, 2005.

[2] SERGIY K. Counter-examples in calculus [M]. Auckland：Mathematical Association of America,2010.

[3] 周民强,实变函数[M].北京:北京大学出版社,2008.

[4] 张筑生,数学分析新讲：第二册,第三册[M].北京:北京大学出版社,2009.

[5] 陶哲轩.陶哲轩实分析[M].王昆扬，译.北京:人民邮电出版社,2008.

[6] 龚光鲁,随机微分方程及其应用概要[M].北京:清华大学出版社,2008.

The Understanding and Analysis onSeveral Well-known Pathological Functions in Calculus

ZHOU Gao-jun, ZHENG Bao-jie

(DepartmentofMathematicsandStatistic,HenanInstituteofEducation,Zhengzhou450046,China)

Four well-known pathological functions in calculus are discussed, and both the history and the important property of the functions are introduced. The functions have double purposes： on the one hand, they allow us to understand the important role of the pathological functions in the development of calculus; on the other hand, they can also further enhance our understanding of the corresponding concepts and conclusions in calculus.

pathological function; Dirichlet function; Cauchy function; Riemann function; Weierstrass function

2014-04-08

河南省软科学项目(132400410105)；河南省教师教育研究课题(2013-JSJYYB-116)

周高军(1968—),男,河南郑州人，河南教育学院数学与统计学院讲师.

10.3969/j.issn.1007-0834.2014.04.009

O174.1

A

1007-0834(2014)04-0035-03