0-1整数规划模型中逻辑表达式的一些注记

张小勇， 贾利新

(信息工程大学 第三学院，河南 郑州 450004)

0-1整数规划模型中逻辑表达式的一些注记

张小勇， 贾利新

(信息工程大学 第三学院，河南 郑州 450004)

从建立0-1整数规划模型的实际出发，对该模型中若干逻辑表达式线性表示、互斥和乘积表达式转化，以及具体的指派问题中能力限制约束的表示问题进行了研究，利用真值表等工具给出了相应的结果.

0-1整数规划；二值变量；真值表

0 引言

优化模型是最为重要的数学模型之一[1- 2].如果在优化模型中决策变量取0和1的二值变量，则称此模型为0-1整数规划模型.0-1整数规划模型是一类重要的优化模型，在指派问题、配送问题等求解中发挥着重要作用[3]112-115.本文从建立0-1整数规划模型的实际出发，对该模型中若干逻辑表达式线性表示、互斥和乘积表达式转化以及指派问题中能力限制约束的表示问题进行了研究，给出了相应的结果.

1 约束条件的线性逻辑表达式表示

在0-1整数规划模型的建立过程中，要将已有的约束条件用逻辑表达式具体地表示出来，同时要求尽可能使用线性约束，以便于利用各类软件或智能算法求解模型[4]. 在露天采矿问题[5]中，一个重要的约束条件为“欲挖下面的1块，必须先挖取上面的4块”.设定上面4块用二值变量a,b,c,d表示，而下面1块用e表示，为了深入解决如何用线性逻辑表达式表达该约束的问题，考虑更一般的情况，即

“如果完成工作A，则必须完成工作A1,A2,…,An”

(1)

的线性表达问题.为此，假设有n项工作A1,A2,…,An.为工作Ai设定一个决策变量xi. 如果决策变量xi取0，表示不完成工作Ai，如果xi取1，表示完成工作Ai.考虑在(1)中n=1的情况，即约束条件“如果完成工作A，则必须也完成工作B”的线性表达问题，设其可以用A→B表示.考虑蕴含式A→B的真值表，A→B为假当且仅当A真而B假[6]，即a=1且b=0，其他情况下A→B均为真(表1).

表1 A→B的真值表

表的真值表

结论1 1) 约束条件“如果完成工作A，则必须也完成工作B”可以用表达式a≤b表示；

2) 约束条件“如果完成工作A，则不能完成工作B”可以用表达式a+b≤1表示；

3) 约束条件“如果不完成工作A，则必须完成工作B”可以用表达式a+b≥1表示.

显然，根据1)，约束条件“工作A工作B必须同时完成”等价于a=b.

注意，“在n个工作A1,A2,…,An中，选择完成的工作不超过k(≤n)个” 可以用∑xi≤k表示；“在n个工作A1,A2,…,An中，选择完成的工作恰好为k(≤n)个”可以用∑xi=k表示.那么“完成工作A1,A2,…,An”等价于“x1+x2+…+xn=n”；“完成工作A1,A2，…,An的至少一个”等价于“x1+x2+…+xn≥1”.把结论1中的结果推广到一般情况，同样利用蕴含式的真值表得到结论2.

结论2 1) 约束条件“如果完成工作A，则必须完成工作A1,A2,…,An”用na≤x1+x2+…+xn表示；

2) 约束条件“如果完成工作A，则必须完成工作A1,A2,…,An中至少一个”可用a≤x1+x2+…+xn表示；

3) 约束条件“如果完成工作A1,A2,…,An，则必须完成工作A”用a+n-1≥x1+x2+…+xn表示；

4) 约束条件“如果完成工作A1,A2,…,An中至少一个，则必须完成工作A”可用a≥x1+x2+…+xn表示.

需要指出，对于结论2中的1)，也可用

a≤x1·x2·…·xn，

或者

a≤min{x1,x2,…,xn}

表示，只是非线性表达式将导致求解的困难.于是，对于露天采矿问题中问题(1),可用

4e≤a+b+c+d

表示.

2 互斥和乘积逻辑表达式的转化

在某些优化问题中还会遇到互相排斥的条件，此时可以人为引入0-1变量，使其变为0-1整数规划.比如对于约束条件“工作A和工作B同时只能选中一个,即A和B有且仅有一个可以完成”.令a,b为二值变量，那么可以用a+b=1表示.

如果在某个优化问题中约束条件f(x)≤0，g(x)≤0只能两者选一，可以引入二值变量t，令

tf(x)+(1-t)g(x)≤0,t∈{0,1}，

便可把两个约束在同一问题中统一.更一般地，如果n个约束

fi(x)≤0,i=1,2,…,n

中同时只能有一个满足，那么引入n个二值变量ti,

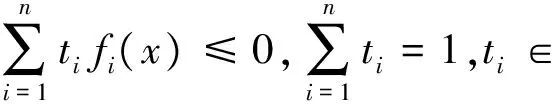
如果约束条件是乘积形式，比如b3=b2b1,bi∈{0,1}，此时如何转化为线性约束？写出4种b1,b2的组合和b3相应的取值，可得

b3≤b2,b3≤b1,b3≥b1+b2-1.

类似地，可以分析乘积约束b=bn…b2b1,bi∈{0,1}的线性表示法.

3 指派问题中能力限制约束的表示

假设cij表示在指派问题中第i人完成第j项工作的所用时间(最小化问题中)或带来的收益(最大化问题中).有时会遇到第i人不能完成第j项工作的约束，此时如何确定对应的cij的取值.

例1[3]126第i人不能完成第j项工作，此时将不会带来任何的收益或者有任何的付出，是否第i人不能完成第j项工作等价于cij=0？假设第1人不能完成第4项工作，将效率矩阵中的c14=4改为c14=0，求解后得到x14=1，这与假设矛盾.考虑极端的情况，假设所有的cij=0，那么此时随意安排xij，都会取到相同的目标函数值0.特别地，取xii=1，也会得到目标函数值为0，这意味着指定第i人完成第i项工作，与所有cij=0矛盾.

如果第i人不能完成第j项工作时令cij取负数，两者是否等价.同样将c14=4改为c14=-2，求解后得到x14=1，矛盾.

第i人不能完成第j项工作，即要保证在解中xij=0.在最小化问题中，根据求解指派问题的匈牙利算法，cij所在的第i行或者第j列cij最大，这样无论如何变换，cij所在的位置不可能为0，从而可以保证xij=0，于是在理论上应该令cij=+∞或者cij=-∞.在实际中只需要求cij相对于其他系数cij充分大(最小化问题)或者充分小(最大化问题)，即取cij为一个大的整数或者大的负数即可.在例1中将c14=4改为90，经过计算得到x14=0，达到了预期目的.

4 结束语

在建立0-1整数规划模型的过程中，本文所提到的约束条件的逻辑表达式的表示和转化问题会经常遇到.通过罗列蕴含式的真值表，或者条件的所有组合以及相应的结论，归纳出对应条件的逻辑表达式.

[1] MEERSCHAERT M M.数学建模方法与分析[M].刘来福，杨淳，黄海洋，译.北京：机械工业出版社,2008：12-17.

[2] 胡运红.数学建模中的最优化理论[J].运城学院学报,2005,23(5):45-48.

[3] 《运筹学》教材编写组.运筹学[M]. 北京：清华大学出版社,1990.

[4] 袁新生,邵大宏,郁时炼.LINGO和EXCEL在数学建模中的应用[M]. 北京：科学出版社,2001:89-95.

[5] 刘翔,徐香勤.基于改进遗传算法的露天采矿优化[J].河南教育学院学报：自然科学版,2007，16(2)：25-28.

[6] 方世昌.离散数学[M].西安：西安电子科技大学出版社,1985:12-35.

Some Notes on Logical Expressionin the 0-1 Integer Programming Model

ZHANG Xiao-yong， JIA Li-xin

(TheThirdInstitute,InformationEngineeringUniversity,Zhengzhou450004,China)

From the practice of modeling 0-1 integer programming, the linear denotation of logical expression, transformation of mutual exclusion and multiply expression are researched, especially the expression of ability constrained condition in assignment problem. Based on the truth table the corresponding conclusions are given.

0-1 integer programming; two-valued variable; truth table

2014-06-01

国家自然科学基金(10501053)

张小勇(1979—)，男，陕西西安人，信息工程大学第三学院讲师.

10.3969/j.issn.1007-0834.2014.04.002

O221.1

A

1007-0834(2014)04-0008-03