Fitts’ 定律实验的设计与实现

樊丽华，王晓英，严海芳，王晓青

Fitts’ 定律实验的设计与实现

樊丽华，王晓英，严海芳，王晓青

首先，介绍了Fitts’定律，然后，设计了验证Fitts’定律的实验，最后，使用Matlab7.0.1对数据进行了统计和分析。实验结果有效地验证了Fitts’定律，并且Fitts’Law（错误率为4%） 得到的预测模型精度高于通过“effective width”Fitts’ Law 得到的预测模型。

Fitts’定律；预测模型；距离；大小

0 引言

Fitts’定律是1954年由美国的Fitts博士提出[1]，是人机交互界面（HCI）使用最广泛的模型之一[2]。随着人机交互领域的应用和发展，Fitts’定律作为一种定量预测模型越来越被广泛的应用[3]。

在本文中，首先对Fitts’定律的模型进行详细的介绍，然后对该实验进行了详细设计，实验的要素包括参与者、设备、任务、实验过程，实验的目的是验证Fitts’定律的有效性，最后对该实验的结果进行分析，建立预测模型。

1 Fitts’定律

Fitts’定律指的是使用指点设备到达一个目标的时间同以下两个因素有关：设备当前位置和目标位置的距离（A），也就是说距离越长，所用时间越长；目标的大小（W），也就是说目标越大，所用时间越短。费茨定律的数学公式如下。Fitts’ Law（错误率为4%）模型，如公式（1）：

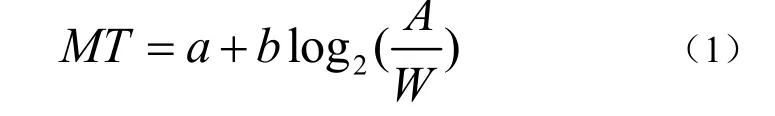
在公式（1）中：A表示移动的幅度，W表示目标的宽度，MT表示移动时间。a，b由实验设备决定。“effective width” Fitts’ Law 模型，如公式（2）：

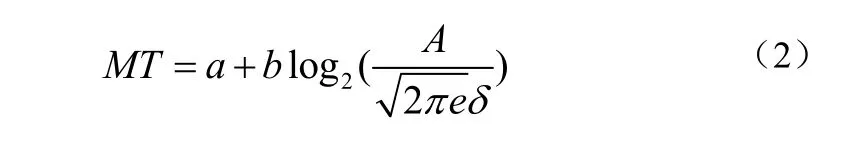
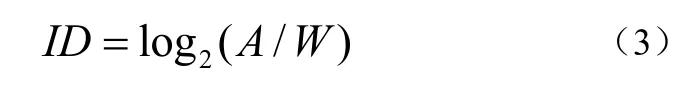
流量TP，如公式（4）：

其中，IDe表示有效的实验难度，如公式（4），MT表示完成实验的时间，TP表示人处理信息的速率，用bit/second表示。其中We=4.1333*δ如公式（5）

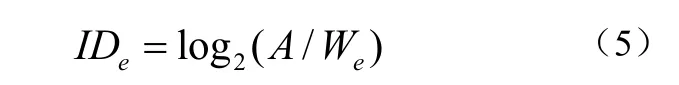
2 实验

2.1 参与者

参与者共8人，其中男士3人，女士5人，年龄30-40岁，学历本科以上，职业大学教师，使用电脑的频率较高。

2.2 设备

实验设备是IBM ThinkPad X61，操作系统Microsoft Windows XP professional，屏幕大小12.1英寸。实验软件界面如图1所示：

图1

2.3 任务

本实验用来验证Fitt’s Law的正确性，对参与者的任务分为两部分：目标大小W固定，改变目标距离；目标距离不变，改变目标大小，要求参与者使用鼠标完成“点击”任务。

如图2所示：

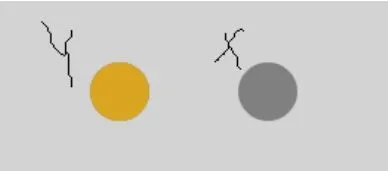
图2

X、Y是两个已设定好尺寸、距离的点。“点击”是指“点击黄色的圆开始测试，测试过程中需要来回点击两个圆直到弹出结束对话框”。

2.4 实验的假设

（1） 同一策略假设，同一位参与者不管距离目标组合是什么，都会使用类似的策略去执行动作。

（2） 相同的距离会花费相似的移动时间，在准备执行动作时会根据距离决定手腕的移动。

（3） 相同的目标区域大小花费相似的瞄准时间，瞄准动作阶段直接被区域宽度影响。

（4） 实验假设以Fitts’ Law定律为基础，假设任务的难度与公式计算出的难度相同。

2.5 设计

本实验中有8个参与者完成鼠标点击3个目标距离A=100，200，400pixels，3个目标大小W=10，20，40pixels相交的实验，共得到9个自变量，即移动时间MT。

根据对受试间设计和受试内设计的定义及比较，HCI设计更偏爱受试内设计[2]。本实验中，由于男女人数不等，没有分组，因此只有受试设计，没有受试间设计。

2.6 实验的过程

在正式实验开始之前，施测者简要讲解实验内容，每一个参与者对给定参数的实验进行“测试次数为3次”的练习，使参与者熟练实验内容。施测者发出实验命令“以舒适的速度”完成实验。

3 结果的处理

3.1 数据的收集和记录

收集8个参与者完成“点击”任务的文本，每一组文本会记录一个参与者完成所有任务的相关数据。参与者“flh1”完成1次“点击”任务的实验数据如表1所示：

表1

w是目标大小，A是目标距离，TargetY、TargetX是点X和Y的起始坐标、具有固定值；EndpointY和EndpointX是X和Y的落点坐标、值由每次点击的实际位置决定；Time是完成相应参数的一次点击的时间。

在一组“测试数据”的文本中会有9*19行数据，代表每个参与者完成重复19次的3*3=9个不同目标大小和距离组合的实验任务。对每个任务收集到的19行数据，为了减少误差去掉前2行数据，分别计算9个变量对应的Time的 17次的平均值。

3.2 数据的分析

（1）数据分析的方法

使用Matlab7.0.1对数据进行分析，计算9个变量对应的8个参与者完成任务的时间MT求平均值mean，标准差SD，使用函数anoval进行单因素方差分析，计算p值。当固定A，改变W时对应的mean，SD和p如表2所示：

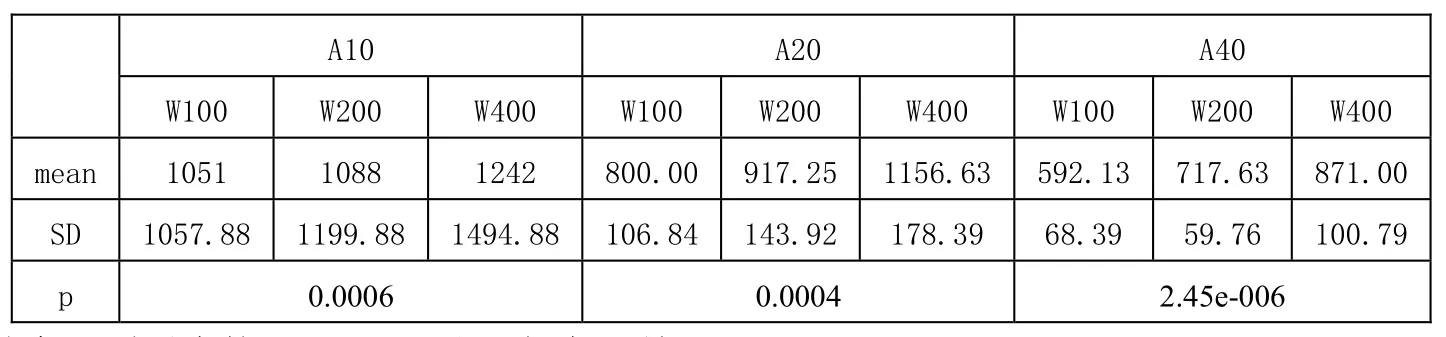
表2

当固定W，改变A时对应的mean，SD和p如表3所示：

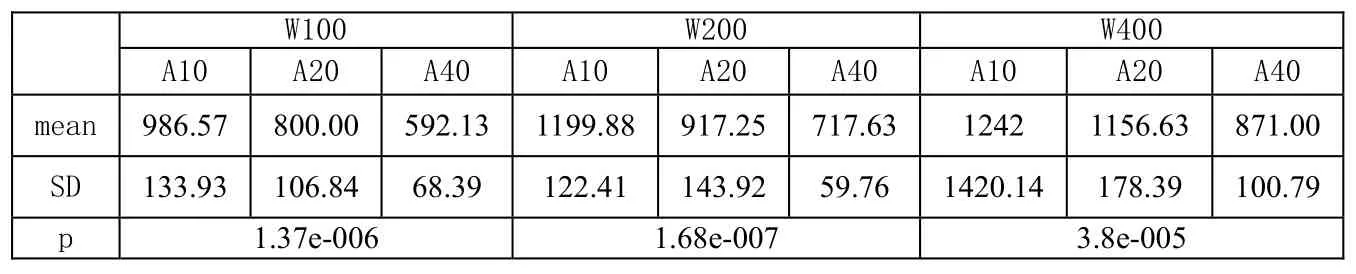
表3

根据单因素方差分析的原理，所有的p＜0.05， 以表2中A=10，W=100，200，300为例，当A固定为10时，不同的W下完成时间有显著的差异，其它同理。

（2）建立预测模型

每一个A-W对应的MT通过计算8个参与者的平均值得到。每一个We通过We=4.1333*δ计算获得，δ是落点坐标的标准差，通过计算每一个A-W下的8个参与者所有的落点坐标的值的标准差获得如表4所示：

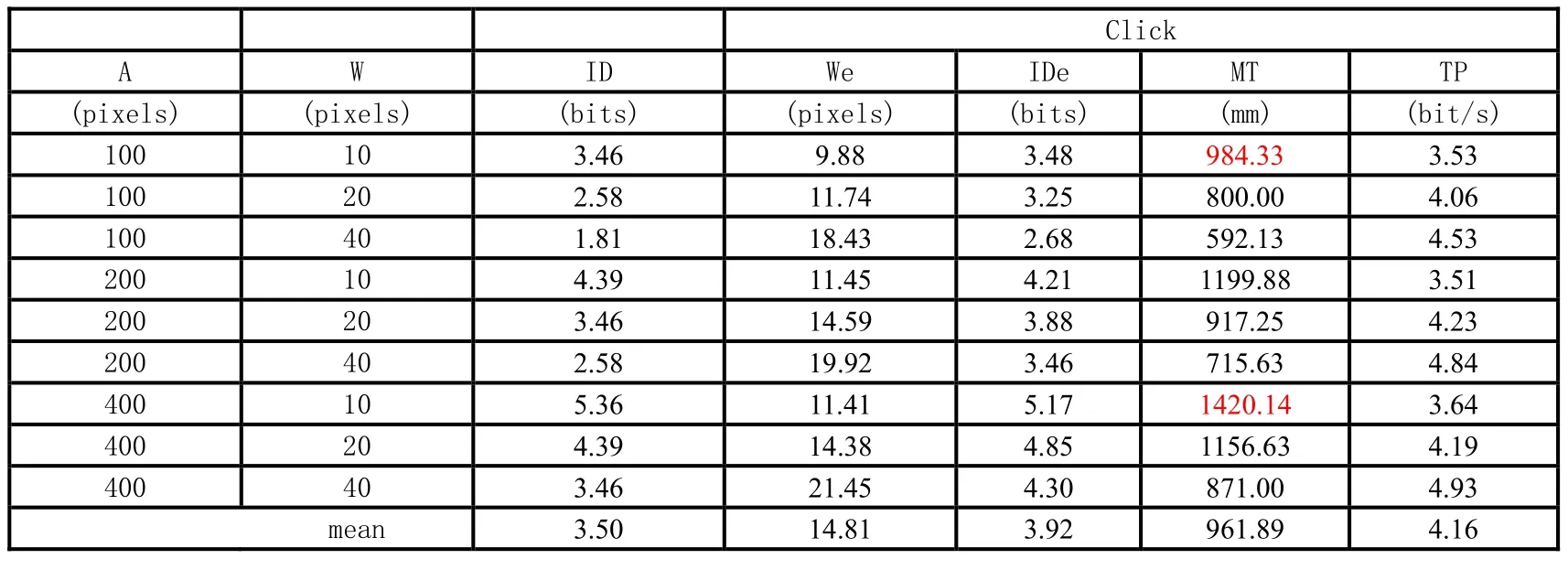
表4

（3）预测Fitts’ Law（错误率为4%） 模型，如公式（1）。

通过图5中的数据使用回归法，建立该预测模型公式（6），其中a=144.68，b=233.64。图3是中X坐标代表完成任务的理论ID，Y坐标代表完成任务的时间，每一个点表示X和Y的关系，如图3所示：

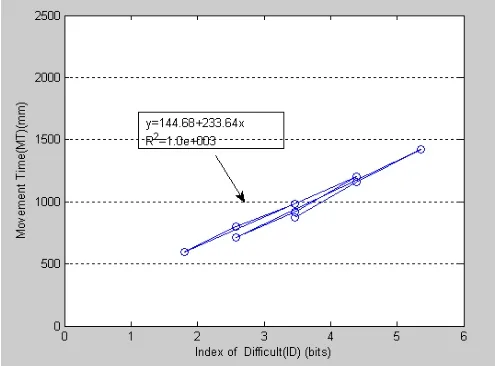
图3

还包括了使用回归方程和R2。对于鼠标“单击”任务，移动距离A选择一个目标大小为W，使用的预测时间如公式（6）：

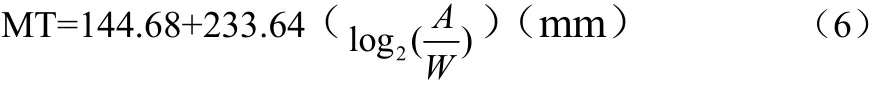
其中，可决系数R2=1.e+003，模型的估计方差是^δ2=2.1591。使用回归方程点预测当A=20，W=200时的y

（4）预测“effective width” Fitts’ Law 模型，如前所示公式（2）：

同理，通过图5中的数据使用回归法，建立该预测模型公式（7），其中a=173.66，b=290。如图4所示：

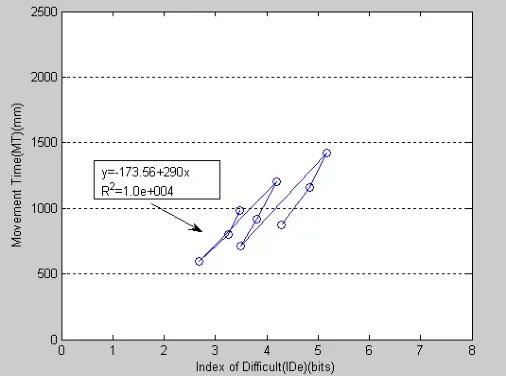
图4

X坐标代表完成任务的实际IDe，Y坐标代表完成任务的时间，每一个点表示X和Y的关系。图4中还包括了使用回归方程和2R。对于鼠标“单击”任务，移动距离A选择一个目标大小为W，使用的预测时间如公式（7）：

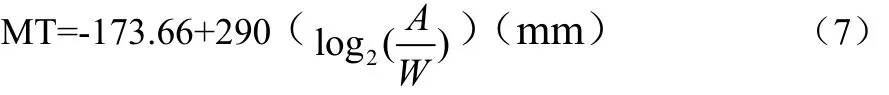
其中，可决系数R2=1.e+004，模型的估计方差是^ δ2=1.6871。使用回归方程点预测当A=20，W=200时的y

4 总结

通过实验结果分析，可以得出，指点设备到达一个目标的时间：设备当前位置和目标位置的距离越长，所用时间越长；目标越大，所用时间越短。此外，通过Fitts’ Law（错误率为4%）得到预测模型精度高于通过“effective width”Fitts’ Law 模型。图4直观显示9个点基本拟合为一条直线，而图5直观显示9个点拟合为3条平行的直线,实验存在一定的误差。原因总结为，参与者的数量较少并在实验过程中有烦躁情绪，而且对参与者训练次数不够，通过实验平台收集的数据中存在大量的遗漏。

[1] P. M. Fitts. The information capacity of the human motor system in controlling the amplitude of movement [J]. Journal of Experimental Psychology, 1954, 47(6): 381-391

[2] I.Scott , MacKenzie. Human-Computer Interaction[M],Elsevier,2013-01-11

[3] 魏先民.人机交互领域中Fitts’定律研究[J]. 制造业自动化，第34卷第3期2012-3(下) .

The Design and Implement of the Experiment of Fitts’ Law

Fan Lihua,Wang XiaoYing,Yan Haifang,Wang Xiaoqing
（1.Computer Department,Qinghai University, Xining810016, China; 2.Basic Department, Qinghai University,Xining810016,China）

This paper firstly introduces the Fitts' law, then designs an experiment to verify this law, finally uses Matlab7.0.1 for data statistics and analysis. The experiment result effectively validates the Fitts' Law to a certain extent, and the accuracy of the prediction model by Fitts' Law (the error rate is 4%) is higher than the predictive model by the "effective width" Fitts' Law model.

Fitts’ Law; the Prediction Equation; Amplitude; Width

TP311

A

2014.06.23）

国家自然科学基金（61363019），青海大学高层次人才科研启动专项基金（QGC-11），Google助力西部教育项目人才引进励教金（2013.12-2014.12）

樊丽华（1982-），女，青海互助人，青海大学，计算机系，讲师，硕士。研究方向：人工智能、人机交互等，西宁，810016

王晓英（1982-），女，青海大学，计算机系，教授、博士，主研方向：高性能计算，云计算，并行计算，西宁，810016

严海芳（1970-），女，藏族，青海西宁人，青海大学基础部，副教授，硕士，研究方向：概率统计，西宁，810016

王晓青（1964-），女，陕西彬县人，青海大学，计算机系，教授，研究方向：数据挖掘，西宁，810016

1007-757X(2014)08-0008-03