时间序列分析在某滑坡变形监测预报中的应用

闫利成 李国辉 张建龙

(内蒙古铁道勘察设计院有限公司，内蒙古呼和浩特 010050)

时间序列分析在某滑坡变形监测预报中的应用

闫利成 李国辉 张建龙

(内蒙古铁道勘察设计院有限公司，内蒙古呼和浩特 010050)

为了预防滑坡的发生，需要不断对监测点的高程进行测量，观测其变化，并对滑坡的动态变化做出预报。在简要介绍时间序列模型的基础上，以某露天矿滑坡为例，对某监测点数据平稳化处理建立差分回归模型，分析模型的应用。计算结果表明，预报趋势基本符合滑坡动态发展规律，进而说明运用时间序列分析法对滑坡变形监测进行预报可行。

时间序列 差分回归模型 滑坡 变形监测

对滑坡变形进行监测预报是一项重要的研究内容。滑坡有着巨大的破坏力，一旦发生，可以损坏建筑、破坏农田、中断交通等，往往会造成大量的人员和财产损失[1]。加强对滑坡变形的监测预报，对于做好防灾减灾工作有着积极意义。

滑坡是一个动态的变化过程，尽管导致滑坡发生的因素很复杂，除内部岩土性质结构外，还有水、采矿爆破振动等外界影响因素[1]，不考虑众多力学影响因素，作为最终表现形式的监测点前后各期高程变化之间存在着一定联系。高程变化是一组依赖于时间t的随机序列，t可视为影响高程变化各种因素的一个综合量。通过大量观测得到的监测点高程变化数据，建立数据随时间动态变化、反映相互关联的模型，进而对其进行预报。

1 时间序列分析

时间序列是一种描述动态数据统计特性的方法，分为确定性变化分析和随机性变化分析。确定性变化包含趋势变化和季节变化等，趋势变化是指具有趋势变化的数据随时间按照一定的规律表现为持续增长或下降，常用分析方法有：移动平均法、指数平滑法、模型拟合法等；季节变化是指受季节等外界客观事物的影响，数据按照一个固定周期有规律的变化，常用的方法是季节指数法[2]。随机性变化不同于上述确定性变化，是由许多不确定因素共同作用引起的序列变化，所使用的分析方法是时间序列分析法。

1.1 时间序列法常用模型[3，4]

(1)自回归模型(AR(p))模型

(1)

(2)

(2)滑动平均模型(MA(q))模型

(3)

若采用后移算子Bqat=at-q，(3)式可以写成

(4)

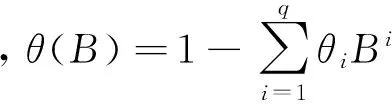
(3)自回归滑动平均模型(ARMA(p，q))模型

Yt=φ1Yt-1+φ2Yt-2+…+φpYt-p+at-θ1at-1-

(5)

采用后移算子(5)式可以写成

(6)

(4)非平稳时间序列模型(ARIMA(p，d，q))模型

实际问题中许多数据不具有平稳性，对于非平稳情形，需要对Yt序列d阶差分，形成平稳的时间序列模型，通常经过一次或两次差分就会稳定下来[5]。该过程实质上是先对观测数据d阶差分，然后再拟合ARMA(p，q)模型。引入差分算子

=1-B有

(7)

其中φ′(B)=φ(B)d

这时φ′(B)=0有d个根在单位圆上，其余根在单位圆外。

1.2 时间序列法预测问题的步骤

(1)模型初步识别

利用自相关系数(acf)和偏相关系数(pacf)来识别，计算公式为

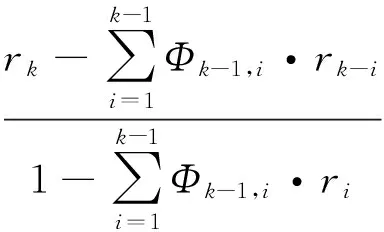
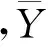
rk和Φkk的分布渐进于正态分布

对于AR(p)模型，它的自相关系数随时滞k衰减呈正弦波或指数，并趋于零，称为“拖尾性”，偏相关系数在p步之后迅速减为零，称为“截尾性”。对于MA(q)模型则有自相关系数q步截尾，偏相关系数呈拖尾性。ARMA(p，q)模型自相关系数和偏相关系数同时具有拖尾性。

(2)参数估计

主要方法有Y-W法、矩估计法、极大似然估计法、牛顿-拉夫森法、最小方差法、最小二乘法等。采用最小二乘法，将(5)式改写为下面形式

(8)

将(8)式表示为向量形式Y=F(X，β)+e

其中Y=[Yp+1，Yp+2，…，YN]T，F=[fp+1，fp+2，…，fN]T，e=[ap+1，ap+2，…，aN]T

X表示观测值Y1，…，YN，β表示待求参数φ1，…，φp，θ1，…，θq

应用最小二乘就是要使残差平方和

Q=[Y-F(X，β)]T[Y-F(X，β)]达到最小来求参数β。

(3)模型检验

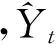
对p阶自回归模型有

Yt=φ1Yt-1+φ2Yt-2+…+φpYt-p+at

对p-s阶自回归模型有

检验Yt-p+s+1，Yt-p+s+2…Yt-p是否对回归模型有显著性影响，若有显著性影响，则选择第一个模型，否则选择第二个模型。

H0:φp-s+1=φp-s+2=…=φp=0

H1:φp-s+1≠0，φp-s+2≠0，…，φp≠0

若H0成立

若H1成立

采用准则函数确定具体阶数时要求使AIC最小，当数据样本N较大时，ARMA(p，q)拟合的最小阶数应使得

(4)模型预报

时间序列建模的主要目的是监测预报，在经过上述模型识别、参数估计、模型检验三个关键步骤后，完成了建模过程。下一步使用建立好的模型对露天矿滑坡监测点高程变化进行预测。平稳时间序列模型(5)式以t+l代替下标t并两边取期望

E(Yt+l)=φ1E(Yt+l-1)+φ2E(Yt+l-2)+…+

φpE(Yi+l-p)+E(at+l)-θ1E(at+l-1)-

E(at+j)=0，j=1，2，3…

2 实例分析

某滑坡位于内蒙古锡林郭勒盟西乌珠穆沁旗境内，所在区域为丘陵山区，剥蚀堆积地形，地质构造复杂，在不断开挖过程中边坡受爆破、大型机械作业震动影响强烈，前期开采排土场建在开挖工程周边，不断堆积扩大的排土场对滑坡体压力不断增大，稳定性逐渐变差，加之该矿潜水区含水层属于中等富水性也导致边坡岩土抗剪强度降低，最终产生滑坡。

本工程在进行滑坡变形监测之前需进行方案设计。方案设计就是选用常规或先进的测量手段获取所需变形量及其随时间的变化情况，对测量方法选择、网形布设、监测频率、精度要求作出具体安排。测量方法的选取按精度较高的水准测量或电磁波测距三角高程法进行，监测网布设包括基准点和待监测点组成，基准点应布设在离滑坡体较远的稳定点上，其高程视为不发生变化。待监测点即目标点，布设在滑坡体上，目标点的运动描述了变形体的变形过程，根据目的要求和变形体形状，变形监测网可以布设成一维、二维或三维网，监测频率应根据滑坡体的规模大小、滑坡变形速度、监测点的布设位置及数目综合确定。滑坡测量精度要求使变形值不超过阈值，中误差限定在变形量的0.05至0.1倍内，一般在数毫米至5 cm之间。

以某监测点滑坡前45期变形监测数据分析为例(如表1所示)，说明时间序列模型在该滑坡变形监测预报中的应用。

表1 各期观测值高程 m

2.1 平稳化处理

随机序列平稳性是建立时间序列模型的前提基础，对于非平稳过程可以采用多次差分的方法平稳化，滑坡监测点的高程变化随时间总体趋势是下降的，其中还包含一些无规律的随机因素起作用，是由测量误差引起的。该序列是一个非平稳过程，但前后各期相关性较强，应用模型之前经过一阶差分即可以去除趋势性成为一个平稳过程。利用Matlab系统辨识工具箱提供的有关时间序列预测的函数进行计算[5]，将原始序列经差分去掉趋势性，成为一个平稳过程的图像(如图1所示)。

图1 差分后图像

2.2 阶数的确定

通过计算自相关系数和偏相关系数可以初步确定阶数，自相关系数如图2所示，偏相关系数如图3所示。可以看出，自相关系数变化缓慢具有拖尾性，偏相关系数迅速下降具有截尾性。可以确定这是一个一阶差分自回归模型，初步确定模型阶数为1，即采用ARIMA(1，1，0)。

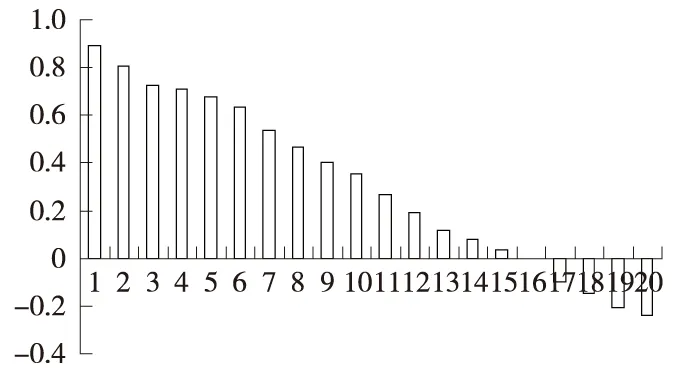
图2 自相关系数

图3 偏相关系数

2.3 参数估计

不同阶数下各参数估计如表2所示。

表2 参数估计结果

2.4 模型检验

以下检验过程给定的统计显著性水平均为0.05，检验ARIMA(1，0，0)与ARIMA(2，0，0)的显著性差异

计算得F=0.8，F0.05(1，43)=4

∵F

检验ARIMA(2，0，0)与ARIMA(3，0，0)的显著性差异

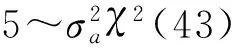
计算得F=0.12，F0.05(1，42)=4

∵F

最终确定为一阶差分回归模型

(10)

2.5 模型预报

采用(10)式对该监测点46～50期高程进行计算，计算结果及与观测值之间的偏差见表3。此外，各期观测值和采用模型的拟合值对比见图4。

表3 测量值与预测值对照 m

图4 测量值与拟合值对比

3 结束语

通过建立差分回归模型，进行滑坡预报研究，预报值和观测值之间的偏差均不超过8 mm，可以保持较高的预测精度，说明模型的建立是合理的。此外，在其他监测点中应用该模型也取得了较高的精度，说明应用时间序列分析对该滑坡变形监测的预测可行。

[1] 肖庆丰，孙连军，王火明.浅谈滑坡成因及防治措施[J].中国水运：学术版，2006，6(9)：106-107

[2] 张树京，齐立心.时间序列简明教程[M].北京:清华大学出版社，北方交通大学出版社，2003:49-54，109-111

[3] 李强，李瑞有.滑坡位移监测动态预报时间序列分析技术研究[J].长江科学院院报，2005，22(6):16-18

[4] 邹积亭.时间序列在建筑物沉降监测数据分析中的应用研究[J].北京建筑工程学院学报，2009，25(2):27-30

[5] 韩路跃，杜行检.基于MATLAB的时间序列建模与预测[J].计算机仿真，2005，22(4):105-107

[6] 刘华夏，张献州.基于时间序列分析的地铁变形监测数据建模与预报研究[J].铁道勘察，2009，35(6):17-19

[7] 吴江淮.基于时间序列分析的变形数据预测[J].铁道勘察，2009，35(1):8-11

[8] 陈青，罗志清，吴芸芸.时间序列在变形监测中的应用[J].江西科学，2011，29(2)：216-218

[9] 田振华，谢忱.基于MATLAB的时间序列在大坝位移预测中的应用[J].河海大学学报:自然科学版,2010，38(2)：170-171

[10]韩路跃，杜行检.基于MATLAB的时间序列建模与预测[J].计算机仿真，2005，22(4):105-107

Applicationforlandslidedeformationmonitoringandpredictionbasedontime-seriesanalysis

YAN Li-cheng LI Guo-hui ZHANG Jian-long

2014-06-16

闫利成(1976—)，男，2008年毕业于北京交通大学交通(铁路)运输工程专业，工程师。

1672-7479(2014)05-0015-04

TB22；TU433

： B