全站仪系统差对三角高程跨河高差的影响分析

吴迪军

(中铁大桥勘测设计院集团有限公司，湖北武汉 430050)

全站仪系统差对三角高程跨河高差的影响分析

吴迪军

(中铁大桥勘测设计院集团有限公司，湖北武汉 430050)

从三角高程跨河水准测量的基本公式出发，探讨全站仪系统差对跨河高差的影响规律及性质，并通过仪器系统差测试实验和工程实例予以验证。理论推导和实例分析结果表明：全站仪系统差的影响可通过对两个仪器位置测回观测高差取平均的方法消除。提出了“只对同一个仪器位置的测回观测高差进行独立限差验算”的新思路，有效地解决了因仪器系统差造成测回观测高差容易超限的问题。

全站仪系统差 三角高程 跨河水准测量 限差验算

自电子全站仪技术1991年被正式编入国家水准测量规范[1]以来，测距三角高程法已逐步取代传统的水准仪倾斜螺旋法，成为跨河水准测量及跨海高程传递中最常用的方法。与倾斜螺旋法、经纬仪倾角法相比，三角高程法具有如下主要优点：(1)两岸仪器及照准点不需要近似等高，场地布设灵活；(2)仪器、标尺及观测员无需频繁换边，测量效率显著提高；(3)适用的跨距范围大，尤其适合于长距离跨海高程传递测量；(4)易于实现外业观测与内业计算的自动化。但因三角高程法应用时间相对较短、影响测量精度的因素复杂和不确定性，仍需在实践中不断进行技术方法的改进与完善。为此，作者曾就跨河场地布置图形、观测方法及程序、限差标准、单标三角高程法等相关问题进行了研究和探讨[2-4]。工程实践中还发现，全站仪系统差导致跨河高差测回互差容易超限，使得原本质量优良的观测成果不合格。在以往研究的基础上，针对全站仪系统差对三角高程跨河观测高差的影响问题进行探讨，分析现行规范[5]中测回高差互差的限差验算方法，提出合理有效的观测成果限差验算方法，以接纳质量可靠的观测成果，提高观测成果的合格率。

1 全站仪系统误差对跨河观测高差的影响分析

由三角高程测量的基本公式[6]，可得仪器置于A点测得跨河边AB的半测回观测高差为

(1)

式中：S——跨河边AB的水平距离/m；

αAB——AB边的垂直角观测值；

iA——A点的仪器高；

vB——B点的觇标(标灯)高。

垂直角观测值中含有两项主要的系统误差，一是全站仪补偿或改正不完全所产生的残余误差，二是对向观测中垂直折光的不对称性系统误差。在式(1)的观测高差中加入该两项误差改正后，得到跨河边AB半测回高差的正确值

(2)

式中：Δ1——A点全站仪(1号仪器)残余仪器误差对观测高差的影响值；

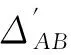
同理，置于对岸B点仪器在相同时段内对A点觇标进行同步或近似同步的对向观测，跨河边BA的半测回高差的正确值为

(3)

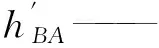
Δ2——B点全站仪(2号仪器)残余仪器误差对观测高差的影响值；

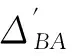
由两岸仪器完成对向观测后，构成一个单测回的观测，则测回高差的正确值为

(4)

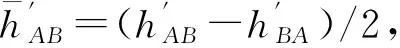
(5)

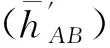
每一个仪器位置的观测完成后，观测员、仪器、标尺应相互调岸，按相同程序进行第二个仪器位置的观测，或在测完半数测回后相互调岸，在第二个仪器位置上完成其余测回的观测[5]。假定两台仪器在两个仪器位置观测期间的仪器残余误差不变，则可仿照式(5)，直接写出第二个仪器位置AB的单测回正确高差的计算式

(6)

由式(5)和式(6)可以看出，两个仪器位置测回高差取中数后可以抵消仪器系统差的影响，但非对称性垂直折光误差的影响不会因此而被消除或削弱。

将式(5)和式(6)两端求差，并经变换后得到两个仪器位置单测回高差的较差

(7)

由式(7)可知，两个仪器位置单测回观测高差之差由三部分组成：第一部分为正确高差之差，第二部分为两台仪器的仪器残差之差，第三部分为两个时段非对称性折光影响之差。

跨河水准测量中，要求在两个仪器位置上具有类似的观测时段(上午、下午、夜间)，即两个仪器位置上非对称性垂直折光影响性质及大小基本相同，因此，式(7)右端第三部分接近于零，而仪器系统差则是造成跨河水准测量系统误差的主要误差来源。鉴于本文重点研究仪器系统差的影响，暂且忽略非对称性垂直折光影响项，则式(7)可进一步改写成如下形式

(8)

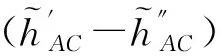
2 仪器系统差测试实验

2.1 场地布设

实验场位于海边一内湾段，场地布点如图1所示，M、N、P三点均钉设带中心标志的水准标灯，其中，M、N位于同一端，P位于另一端；MP、NP跨越海水面，边长约2.5 km，视线高度超过4 m。由于M、N相距很近(约1.5 m)且基本等高，因此可以近似认为MP和NP两条跨海边具有相同或相似的垂直折光影响。

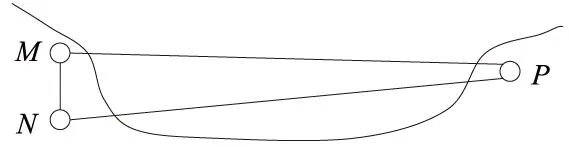
图1 实验场地布点示意

2.2 全站仪校准

实验观测前，按仪器说明书[7]规定的方法和程序进行全站仪校准。3台Leica全站仪的校准参数见表1。表中，l、t为补偿器纵向和横向指标差，i为竖直角指标差，c为视准误差，a为横轴倾斜误差。这些参数中，只有l、i两个参数影响垂直角观测值。

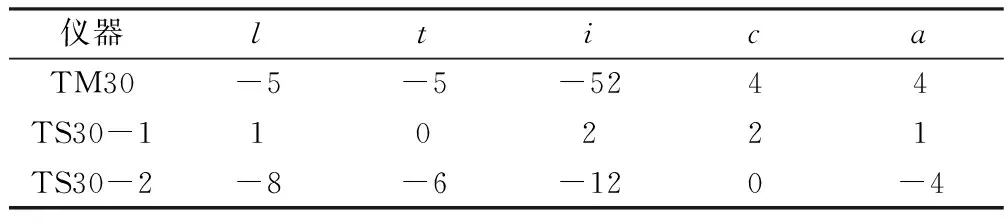
表1 全站仪校准参数 (″)

由表1可见，全站仪TM30的i值偏大，TS30-2次之，TS30-1最小；TM30与TS30-1的i值互差较大(-54″)，两台TS30的i值互差较小(-14″)。三台仪器的i值的绝对值不大且差异较小。

2.3 测试观测

MP、NP的水平距离使用全站仪精密测定，M、N两点之间的高差使用水准测量方法精密测定，垂直角观测选择在气象稳定的夜间进行。将三台全站仪按照l、i差异值的大小分为两组(第Ⅰ组：TS30-1，TS30-2；第Ⅱ组：TM30，TS30-1)，同一组中的两台全站仪分别安置于M、N两点，对P点处的目标(标灯)进行同步同向观测：MP、NP边各测量相同测回数(此处所述1测回，系指跨河水准测量中的半个测回观测)，每测回连续观测8组；每组正、倒镜各照准2次，每次照准各记录1次数据。垂直角观测前、后，采用专用方法精密测定仪器高(iM、iN)和目高程(vP)，量高精度优于0.5 mm。

2.4 观测高差及仪器系统差计算

使用式(1)计算跨海边(MP、NP)的观测高差(hMP、hNP)，利用M、N之间的水准高差(hMN)，将N点仪器测得的观测高差hNP换算成h′MP，并与另一台仪器同步观测高差hMP求差，得到全站仪系统差对观测高差的影响值，即式(7)或式(8)中的(Δ1-Δ2)。两组仪器的计算结果分别列入表2、表3。

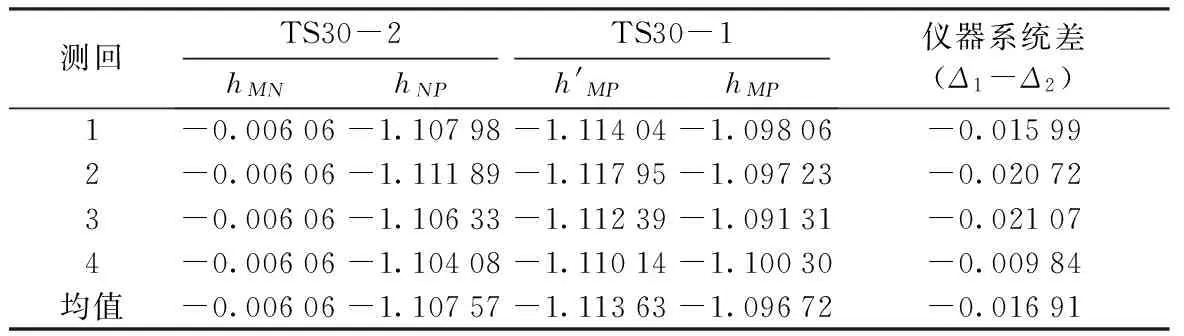
表2 第Ⅰ组全站仪的仪器系统差计算 m

由表2、表3可知，两台TS30的仪器系统差为-0.016 91 m，TM30与TS30-1的仪器系统差为-0.033 06 m。显然，第Ⅱ组仪器的系统差较第Ⅰ组大。而表1的数据显示：第Ⅱ组仪器校准参数的较差比第Ⅰ组大。是否可以因此得出结论：仪器校准参数差值越大，跨河高差中仪器系统差影响也越显著？对此目前尚无定论，有待进一步研究。但作者所从事的大量跨河(海)水准测量实践结果表明：两个仪器位置跨河(海)观测高差中存在显著系统差的情形，均发生在两台全站仪校准参数较差偏大的情况下。

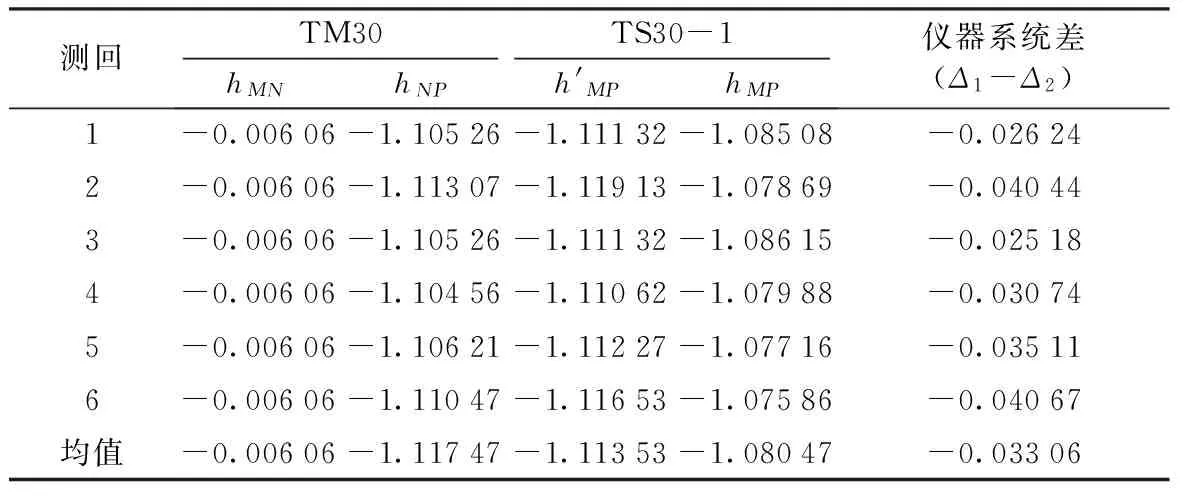
表3 第Ⅱ组全站仪的仪器系统差计算 m

3 工程实例分析

使用上述测试实验中的两组全站仪，按三角高程法进行二等跨海水准测量的对比实验。跨海距离为2 445 m，与仪器系统差测试实验的跨距近似等长，便于进行仪器系统差改正。使用第Ⅰ组全站仪总共观测55个单测回，其中第一、第二两个仪器位置分别观测29测回、26测回；使用第Ⅱ组全站仪总共观测139个单侧回，其中第一、第二两个仪器位置分别观测72测回，67测回。按照两个仪器位置测回数相等的对称选取原则，逐次剔除最大/最小观测值后，再进行观测高差及改正高差的统计计算，结果详见表4。表4中，“单测回改正高差”系利用表2、表3中相应仪器组的仪器系统差(Δ1-Δ2)按式(5)，式(6)计算而得。

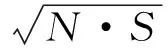
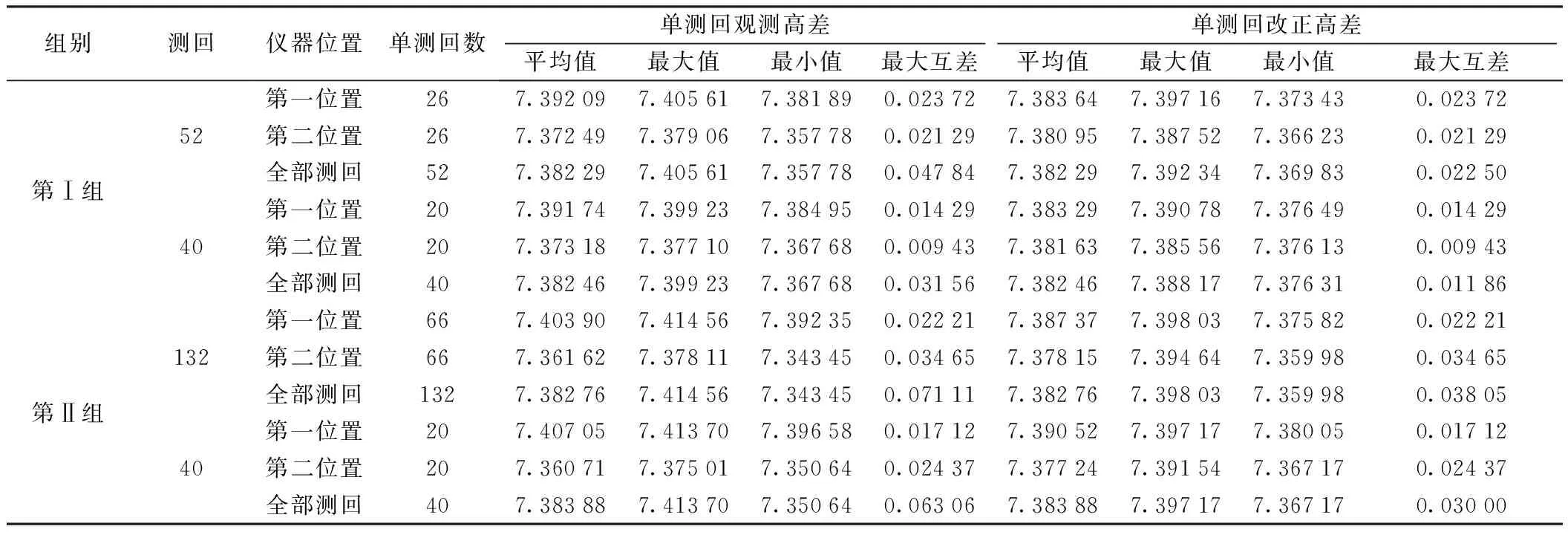
表4 全站仪跨海观测高差统计分析 m

分析表4的统计结果，可得如下主要结论：

(1)第Ⅰ组仪器两个位置的单测回观测高差平均值的互差为：7.392 84-7.372 49=0.020 35 m，改正高差平均值的互差为：7.384 44-7.380 90=0.003 54 m；第Ⅱ组仪器两个位置的单测回观测高差平均值的互差为：7.404 07-7.361 60=0.042 47 m，改正高差平均值的互差为：7.387 54-7.378 13=0.009 41 m。可见：同一个仪器位置的测回观测高差中含有明显的仪器系统差影响，且第Ⅱ组仪器的仪器系统差大于第Ⅰ组仪器，但经系统差改正后的测回高差与正确高差靠近，此结论与仪器系统差测试结果相吻合。

(2)两组仪器、不同测回数计算出的“全部测回”观测高差的总平均值非常接近，最大互差仅为：7.383 88-7.382 29=0.001 59 m，而且改正前、后总平均值相等。由此可见：仪器系统差对观测高差的影响，可通过两台仪器互换位置进行观测取均值的办法来消除，即在观测高差总平均值中不再包含仪器系统差的影响。

(3)单测回观测高差比较，同一个仪器位置的“最大互差”(最大值与最小值之差)全部小于规定限差(40 mm)；但在两个仪器位置合并组成的“全部测回”中，只有第Ⅰ组仪器40个测回的“最大互差”合限，而第Ⅱ组仪器的“全部测回”最大互差均超限，且超限量较多。也就是说，使用第Ⅱ组仪器观测了139个单测回，但却无法按现行规范的要求挑选出足够数量测回数(40个)的合格成果。由此可知：当两台仪器的系统差较大时，尽管同一个仪器位置的测回观测高差互差合限，但两个仪器位置共同构成的“全部测回”观测高差的互差极易超限，更极端的情况是：当系统差过大时，观测成果始终无法合格。

(4)经系统误差改正后，单测回高差的最大互差全部符合规范限差的要求(均小于40 mm)。

4 关于限差验算方法的讨论

现行国家标准《国家一、二等水准测量规范》[5]规定：每条边各单测回高差间的互差dH，不应大于式(9)计算出的限差

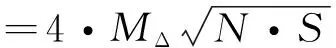
式中，MΔ为每km水准测量的偶然中误差限值，单位为mm；N为总的单测回数；S为跨河视线长度，单位为km。

以上限差公式是基于偶然误差特性推导出来的[2]，未顾及仪器系统差对观测高差的影响，在大多数情况下是适用的。但当对向观测的两台全站仪存在明显的系统差时，若仍按此限差标准进行验算，则很可能出现观测成果合格率下降甚至根本无法合格(如前面工程实例中第Ⅱ组仪器)的现象。导致这种结果的根本原因不是观测质量不高(即非观测成果中偶然误差超标)，而是仪器系统差造成两个仪器位置的测回观测高差的互差增大而超限。因此，按现行规范中的限差标准及方法进行限差验算时，很可能会不合理地舍弃原本合格的观测成果，造成观测量的极大浪费。

为了解决上述问题，可采取如下几种方法或途径：

(1)观测前仔细进行全站仪校准，确保全站仪检校参数的测定精度，最大限度地削弱仪器残余误差。对校准参数过大的全站仪送厂家进行校正，还可规定各参数的检校限值或两台仪器校准参数互差的限值。

(2)适当放宽单测回互差的限差标准[4]。

(3)调整限差验算方法。由目前通行的“对两个仪器位置的全部测回观测值合并进行限差验算”，调整为“只对每个仪器位置的测回观测值进行独立的限差验算，不再进行合并验算”，或者对同一仪器位置的测回观测值、全部测回观测值采用不同的限差标准进行验算”。

以上三种方法可以单独使用，也可综合使用。第三种方法，也就是“调整限差验算方法”，是解决仪器系统误差影响问题的最根本和最有效的方法，具体思路是：按式(9)或文献[4]提出的限差公式对两个仪器位置的测回高差观测值进行独立验算，跨河高差环闭合差仍按现行规范公式或按文献[4]中提出的新的限差公式进行限差验算，两个仪器位置取用相同数量的合格测回数合并求取跨河高差的测回总平均值。显然，在测回总平均值中已经消除了仪器系统差对观测高差的影响。

5 结论

通过理论分析、测试实验及工程实例验证，对全站仪系统误差在三角高程跨河高差中的影响规律及限差验算方法进行了探讨，得出如下主要结论：

(1)全站仪补偿或改正不完全的残余误差会引起跨河水准测量中的系统误差，即仪器系统差。仪器系统差对单个仪器位置的测回观测高差具有不利影响，但可通过两岸仪器调岸观测后取两个仪器位置测回观测高差的均值得以消除或削弱。

(2)仪器系统差的存在会引起两个仪器位置的跨河高差之间的较差增大，因此，按现行规范中的限差验算标准及方法进行成果验算时，会不恰当地舍弃原本合格的观测成果，导致观测成果的合格率降低甚至无法取得符合限差要求的合格成果。为此，提出了三种解决问题的思路，其中以调整限差验算方法为首选。

(3)仪器系统误差主要由全站仪校准误差、补偿器的零位误差等[8]仪器补偿或改正不完全造成，但其具体的影响因素较多且影响规律比较复杂，有待进一步研究和探讨。

[1] GB/T 12897—91国家一、二等水准测量规范[S]

[2] 吴迪军，熊伟，李剑坤.精密测距三角高程跨河水准测量的改进方法[J].测绘通报，2010(3):4-6，20

[3] 吴迪军.单标三角高程法跨河水准测量设计与实验分析[J].地理空间信息，2012，10(4):132-133，136

[4] 吴迪军，许提多，罗苏.关于三角高程跨河水准测量限差的探讨[J].地理空间信息，2012，10(5):105-107

[5] GB/T 12897—2006国家一、二等水准测量规范[S]

[6] 武汉测绘科技大学《测量学》编写组，陆国胜. 测量学[M].北京：测绘出版社，1991

[7] Leica TS30/TM30用户手册1.1版(中文)，Leica Geosystems AG， Heerbrugg， Switzerland

[8] 杨俊志.全站仪的原理及其检定[M].北京：测绘出版社，2004

InfluenceoftheInstrumentalSystematicErroronTrigonometricalRiver-crossingHeightDifference

WU Di-jun

2014-08-12

中国中铁股份有限公司科技开发计划(2012-重大-2)。

吴迪军(1964—)，男，1984年毕业于武汉测绘学院工程测量专业，工学博士，教授级高级工程师。

1672-7479(2014)05-0001-05

P224.2

： A