基于ABAQUS的飞轮壳面压计算及密封胶选择
钱多德,王昊鹏,曹文霞
(1.安徽江淮汽车股份有限公司技术中心,安徽合肥 230601;2.天津内燃机研究所,天津 300072;3.安徽水利水电职业技术学院机械工程系,安徽合肥 231603)
0 前言
发动机后端齿轮室与飞轮壳接触面大,是密封设计中需要重点关注的区域。而密封胶作为一种使用灵活的密封手段,具有锁紧防松、密封防漏、固持定位的特点,在内燃机行业中被大量使用,且不同类型密封胶的使用条件各不相同;因而需要在发动机各个结构得到确定的条件下,确定密封胶的具体选择。随着计算机数值分析技术的发展,采用一定的模拟技术对工程选择做出理论支撑具有十分明显的意义。
1 组件连接的力学模型
文中涉及到的螺栓连接主要有两种形式,如图1所示,图(a)、(b)两图中螺纹孔均位于最下层底板,其余通孔不具有螺纹,螺栓打紧后,使待密封面形成配合。螺栓通过扭矩 (T)控制法拧紧,在CAE模拟中需用公式
将扭矩载荷转化为力 (F)载荷。
在公式 (1)中,K为扭矩系数,计算公式为:
式中:p为螺纹螺距;μ为综合摩擦因数;d2为螺纹中径;De为支承面有效外径;Di为支承面的内径[1-2]。
2 常用密封胶的使用特点
密封胶是机械产品的一种新型密封材料,亦称液态垫片,填充再结合部分,阻止液体的泄漏,具有密封、填塞、衬垫的作用,储存状态为液态及膏状。在发动机装配过程中,常用的密封胶有厌氧胶和有机硅胶,二者适用于不同工作条件。
(1)厌氧胶。从定义上讲,厌氧胶黏剂在氧气存在的条件下保持液体状态,在隔绝氧气并有金属离子如铁离子或铜离子存在的条件下发生固化反应。不需称量、混合、配胶,使用极其方便,容易实现自动化作业。
(2)硅胶。相比于厌氧胶,有机硅胶的固化条件对于空气及湿度的要求则没有那么苛刻,只需在涂抹后放置一段时间,便可固化成型[3-4]。
3 ABAQUS/Standard接触理论
在ABAQUS接触模拟中,通过将接触面的名字赋予一个接触的相互作用来定义两个表面之间可能发生的接触,并赋予一种接触属性。ABAQUS/Standard使用单纯主—从接触算法:一个表面 (从属面)上的节点不能侵入另一个表面 (主控面)的某一部分,并在两面间产生间隙。该算法并没有对主面做任何限制,它可以在从面的节点之间侵入从面,如图2所示。基于这种严格的主从关系,必须根据如下原则选择主面和从面:(1)从面应该是网格划分更精细的表面;(2)如果网格密度相近,从面应该取自采用较软材料的表面。此外,针对两平面的相对滑动,根据量级分为小滑动和有限滑动,如果两个表面之间的相对运动小于一个单元面上特征长度的一个小的比值(如20%),那么小滑动是合适的。在许可的条件下使用小滑动公式可以提高分析的效率[5-6]。
4 有限元模型及结果分析
在建立组件接触有限元模型时,对其受力状况做一定的假设和简化,是在保证研究对象的基本特征和受力状态尽量真实的前提下进行的。
对有限元模型的假设和简化包括:
(1)气缸与机体之间的缸垫予以省略,代之以一定的装配间隙,即二者间无接触。
(2)为减少不必要的运算分析,在对模型影响很小的情况下,将实际结构中存在于缸盖与齿轮室间的密封胶层省略,缸盖与齿轮室间无接触。
(3)为方便划分网格,同时为确保运算分析收敛,将半缸机体、半缸下箱体、半缸盖、飞轮壳中的水套、油道、加强筋等结构予以填充、去除。
(4)建模过程中,不再对螺纹进行精确建模,包括螺纹孔及各型螺栓等处螺纹。
4.1 建立三维模型
取发动机飞轮端的半缸盖、半缸机体、半缸下箱体、齿轮室、飞轮壳及各型螺栓构成组件,并将组件各部分按前述原则简化,如图3所示,各部分均在三维软件Pro/E中建立,并导出为.igs格式,再将其导入Hypermesh中划分网格,生成.inp文件,最后导入ABAQUS软件。
4.2 统一网格装配坐标系
为保证模型组件能在各步软件处理中保持正确的装配关系,此次计算分析采用了基于几何面约束求解全局坐标系的装配定位方法,其基本思想是根据现有三维模型建立部件几何面之间的装配关系,以统一坐标系为媒介,在CAE环境下对部件几何面进行参数表达,从而识别每个几何面的目前位置和方向,并可以在各步所用软件中被继承下来,从而保证了分析过程中装配关系的准确、无误[7-8]。
4.3 划分网格
分别划分各零件的3D网格,网格划分过程要遵循如下几个原则:
(1)合法性。一个单元的节点不能落入其他单元内部,在单元边界上的节点均应为单元的节点,不可丢失。
(2)相容性。单元必须落在待分区域内部,不能落入外部,且单元并集等于待分区域。
(3)协调性。单元上的力和力矩能够通过节点传递给相邻单元。因此,要保证一个单元的节点必须同时也是相邻单元的节点,而不应是内点或边界点;相邻单元的共有节点具有相同的自由度性质,即自由度必须匹配。
(4)逼近精确性。待分区域的顶点 (包括特殊点)必须是单元的节点,待分区域的边界 (包括特殊边及面)被单元边界所逼近。
(5)良好的单元形状。单元最佳形状是正多边形或正多面体。
(6)良好的划分过渡性。单元之间过渡相对平稳,否则将影响计算结果的准确性甚至使有限元计算无法进行下去。
(7)网格划分的自适应性。在待研究接触面、几何尖角处、应力、面压力等变化大的地方网格应密,其他部位应较稀疏,这样可以保证计算结果精确可靠。
(8)一致性。对于相连的两个二次单元,单元角点只能与单元角点连接,而不能与相邻单元的中间节点相连;相邻单元的公共边应具有相同的节点数。
此外,为保证计算精度,接触面网格细化为2 mm,保证节点对应,图3中几何体采用C3D4单元 (4节点四面体线性完全积分单元),共计划分单元995 634个,并利用ABAQUS软件集成的网格检测功能,根据计算迭代要求检查网格质量[9-11]。
4.4 定义材料
各零件材料属性如表1所示。
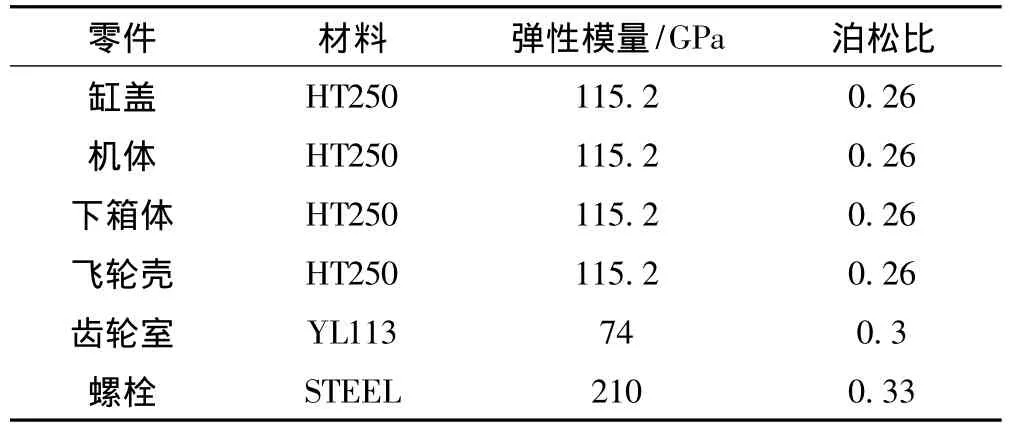
表1 零件列表及材料属性
4.5 定义接触
在ABAQUS软件Interaction功能模块中定义接触面,组件间各接触面及支承面与螺栓接触面赋予τ=0.15的罚函数小滑动摩擦属性,见图4。
4.6 定义边界条件和载荷
根据实际受力情况,用主菜单中的BC→Manger来创建边界条件,用Load→Manger来施加载荷。为了确保收敛,先定义一个只用10 N螺栓轴向力的分析步,让接触关系平稳建立起来;然后在第二个分析步中施加真实载荷,其值由公式 (1)计算,如表2所示,设定细节见图5、图6。

表2 各型号螺栓轴向力
4.7 后处理及结果分析
利用Visualization功能模块进行后处理:显示待密封面——飞轮壳-齿轮室接触面的CPRESS面压力 (图7)及COPEN两密封面分离间隙 (图8)。
在图7可见:接触面上分布的大量深色区域接触面压小于2 MPa,且在图8中,对应浅色区域存在的间隙达到8 μm甚至更大。
将现有计算结果与第2节中所列密封胶使用条件进行比对发现:此结构中多处区域的分离间隙较大,极有可能不满足厌氧胶的使用条件;与之相应的是,硅胶所能接受的密封面最大间隙可达0.6mm,也就是说,硅胶可以对非加工或粗加工表面进行密封。这样,采用硅胶,一方面可以满足此结构的密封要求,另一方面又可以降低生产成本,一举两得。
4.8 接触面压偏小原因分析及改进措施
接触面压偏小的原因主要有:
(1)相邻螺栓间距过大。螺栓打紧后,螺帽挤压支承面,使飞轮壳产生局部翘曲变形,因此,当相邻紧固螺栓间距较大时,远离两螺栓的中间区域会有接触面压不足的情况。
(2)接触面几何形状复杂。飞轮壳局部接触面的曲率变化较大,形成了一些远离螺栓的区域,这样导致作用在接触面上的压力不足,从而产生了局部分离。
(3)相邻接触面紧固螺栓的影响。齿轮室除与飞轮壳配合外,还同机体、下箱体、缸盖存在螺栓连接,也会引起齿轮室的局部变形,影响待密封面的接触。
针对上述原因,相应的改进措施包括:
(1)增加接触面的刚度,保证接触面的压力分布更加均匀,加强筋的设置位置应尽量靠近螺栓处。
(2)螺栓位置分布尽量均匀,在接触面曲率变化剧烈的位置,将螺栓布置得紧密一些。
(3)适当增大螺栓的上紧力矩。
5 结束语
根据待密封面及其相关组件的装配关系,建立了有限元分析模型。
(1)计算得到了面压力及接触面间隙模拟结果,发现存在多处面压力偏小的区域,通过比对厌氧胶和硅胶的使用条件,最终得出结论:推荐选用硅胶作为齿轮室-飞轮壳接触面的密封手段,以期达到在满足密封条件的前提下节约成本的目的。
(2)通过对该结构的分析得出了增加面压、减小间隙的设计原则,对密封接触面的设计具有一定指导意义。
【1】徐超,余绍蓉,郑晓亚,等.机械螺栓法兰联接的有限元力学模型比较研究[J].机械设计与制造,2009(6):37-39.
【2】濮良贵.机械设计[M].7版.北京:高等教育出版社,2003.
【3】邢东仕.发动机液态密封垫片技术[J].新技术新工艺,2013(1):12-15.
【4】陈敏,刘晓叙.现代中、小型柴油机密封设计技术[J].润滑与密封,2001(5):68-69.
【5】石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2006.
【6】庄茁,由小川,廖剑晖,等.基于ABAQUS的有限元分析和应用[M].北京:清华大学出版社,2009.
【7】任强,杨海成,万能,等.有限元网格模型装配技术研究[J].航空计算技术,2011,41(1):87 -92.
【8】许文彬,张华良.基于三角形连接的有限元网格划分[J].计算机技术与发展,2011,21(9):59 -61.
【9】李海峰,吴冀川,刘建波,等.有限元网格剖分与网格质量判定[J].中国工程机械,2012,23(3):368 -377.
【10】NGUYEN D-T,PARK.Finite element method study of incremental sheet forming for complex shape and its improvement[C]//Proceedings of the Institution of Mechanical Engineer,2010:913-924.
【11】LI Y,LIU G R,ZHANG G Y.An Adaptive NS/ES-FEM approach for 2D contact problem using triangular elements[J].Finite Elements in Analysis and Design,2011,47:256 -275.

