含时线性谐振子系统密度算符的研究

范开敏，唐 婧

(1.四川文理学院物理与机电工程学院，四川达州635000;2.四川文理学院化学化工学院，四川达州635000)

含时线性谐振子系统密度算符的研究

范开敏1，唐 婧2

(1.四川文理学院物理与机电工程学院，四川达州635000;2.四川文理学院化学化工学院，四川达州635000)

主要是研究含时线性谐振子系统的量子解问题.首先运用李代数方法得到含时线性谐振子系统的密度算符随时间演化的量子精确解，然后对得到的解析式进行了验证和分析.结果显示，我们得到的含时谐振子系统密度算符的解析解能准确的描述含时谐振子系统密度算符随时间的演化.

含时谐振子；密度算符；量子解

0 引言

在量子力学中，含时哈密顿量系统随时间演变问题,一直是人们感兴趣的一个研究课题，人们对含时系统提出了各种处理方法，如正则变化法、李代数方法、假设波函数法等．[1-3]谐振子是量子力学研究中的一个典型的模型，研究者们对谐振子的研究也比较广泛．[4-6]事实上阻尼谐振子的量子力学处理问题，早在1980年，彭桓武曾较为详细的讨论过阻尼谐振子的量子力学处理问题.[5]随后，朱如曾研究了允许阻尼常数显含时间的阻尼谐振子系统．[6]2002年，Ferreira与他的合作者讨论了谐振子系统处在电磁场中的相关问题，[7]2004年，Liang等人利用假定波函数的方法详细研究过含时线性势系统.[8]作为一个经典的物理模型，谐振子哈密顿量形式表示为：

(1)

(1)式是不显含时间的谐振子的哈密顿量形式.含时线性谐振子系统的哈密顿量的表达式可以写为：

(2)

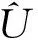
1 理论方法

(3)

含时谐振子系统的哈密顿量算符可以写为如下形式:

(4)

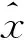
(5)

J+,J-,J0构成三维简单代数,即构成封闭的三维代数空间{J+,J-,J0} ,Jr(r=-,+,0)之间满足如下对易关系:

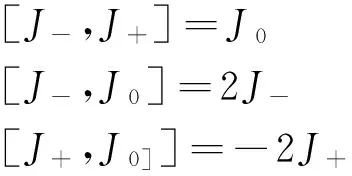
(6)

由于J+,J-,J0构成一个封闭的代数空间，所以该哈密顿系统时间演化算符可以写为：[2]

(7)

其中，系数gr(t)是含有时间的拉格朗日参数.

2密度算符的精确解

含时谐振子系统，在任意时刻t的密度算符记为ρ(t)，我们取t=0为初始时刻时，该系统密度算符为，[9]

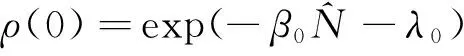
(8)

其中β0=β(t=0)，λ0=λ(t=0).

(10)

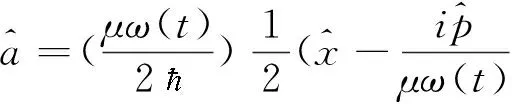
(11)

可以将(8)式用J+,J-,Jo来表示为：

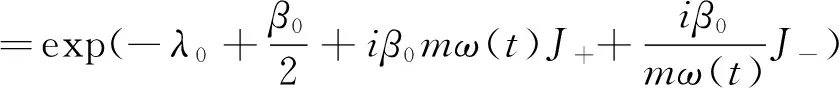
(12)

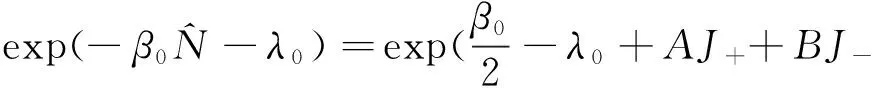
(13)

这样由(7)式和(13)式可以给出，含时谐振子系统任意时刻t密度算符ρ(t)的表达式：

(14)

(15)

就可以得到ρ(t)的形式表达式:

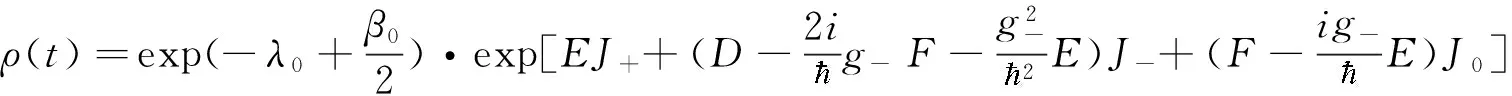
(16)

其中：

(17)

把(5)式和(17)式带入(16)式可以得出，在任意时刻密度算符的形式解：

(18)

其中，拉格朗日参数gr(t)满足一组微分方程，[2]且满足初始条件：gr(t=0)=0,(r=-,+,0).以积分的形式表现出来：

(19)

这样就得到含时线性谐振子系统密度算符随时间演化的一个形式解.如果Ar(t)有确定的解析式，由方程(19)式能够解出gr(t)的解析式，然后通过(18)式可以得到任意时刻密度算符的精确解.

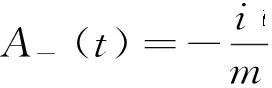
(20)

这时求得哈密顿量不显含时间t时密度算符的解析式：

(21)

进一步，当我们取t=0时，即初态，(21)式退回初态ρ(0)的表达式.

2 结论

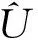
[1] 凌瑞良．含时阻尼线性谐振子的量子不变量处理[J]．大学物理，2007(12)：12-15．

[2] Fan K M, Zheng Y J, Ren W Y and Ding S L.Exactquantumsolutionsofgeneraldriventime-dependentquantumquadraticsystem[J]. Int.J.Quant.Chem., 2006(107):1355-1366．

[3] 梁麦林，孙宇晶．一般含时线性势的量子解及有关问题[J]．物理学报，2004(11)：3663-3667．

[4] 阎新云，安吉庆．谐振子的传播子[J]．新疆大学学报，1995(1)：58-61．

[5] 彭桓武．阻尼谐振子的量子力学处理[J]．物理学报，1980(8)：1084-1089．

[6] 朱如曾．关于阻尼谐振子的量子力学处理[J]．物理学报，1981(10)：1410-1414．

[7] Ferreira C A S, Alencar P T S, and Bassalo J M F.Wavefunctionsofatime-dependentharmonicoscillatorinastaticmagneticfield[J]. Phys. Rev. A, 2002(66):024103.

[8] Liang M L, Zhang W L.Forcedtime-dependentharmonicoscillatorinastaticmagneticfield:exactquantumandclassicalsolutions[J]. Int. J. Theor. Phys. 2003(42):2881-2889.

[9] Alhassid Y and Levine R D.Connectionbetweenthemaximalentropyandthescatteringtheoreticanalysesofcollisionprocesses[J]. Phys. Rev. A, 1978(18):89-116.

[10]曾瑾言．量子力学卷Ⅰ[M]．北京：科技出版社，2000：255-256．

[责任编辑 邓 杰]

A Study of Density Operator of Time-dependent Linear Harmonic Oscillator System

FAN Kai-min1, TANG Jin2

(1. Physics and Engineering Technology Department of Sichuan University of Arts and Science, Dazhou Sichuan 635000;2. Chemistry and Chemical Engineering Department of Sichuan University of Arts and Science, Dazhou Sichuan 635000, China)

In the paper, the time-dependent linear harmonic oscillator system has been studied. Firstly, the exact quantum solution of density operator of the time-dependent linear harmonic oscillator system has been obtained by using Lie algebra method. Secondly, the analytic expression has been tested and discussed and it shows that the analytic expression of density operator can well describe the process for time evolution of density operator.

Time-dependent armonica oscillator; density operator; quantum solution

2013-12-11

四川省教育厅科研基金(11ZB141)；四川文理学院校级科研基金(2012Z008Y)

范开敏(1978—)，男，山东日照人.讲师，博士，主要从事材料结构与性能、理论物理研究.

O413.1

A

1674-5248(2014)02-0038-03