完美匹配单圈图的hyper－Wiener指标

侯远，郑艺容

（1.福州大学 至诚学院，福建 福州 350002；2.厦门理工学院 应用数学学院，福建 厦门 361024）

在化学理论中，基于分子图的顶点间距离的拓扑指标对刻画分子图以及建立分子结构和特征间的关系有重要作用，同时被广泛用于预测化合物的物理化学性质和生物活性.Randic＇在1993年提出了无圈图的hyper－Wiener指标的定义，之后klein等人［1－3］将Randicc＇的定义推广到所有连通图.顶点u和v 间的距离d（u，v｜G）表示顶点u和v 之间最短路的长度，则图G 的hyper－Wiener指标为

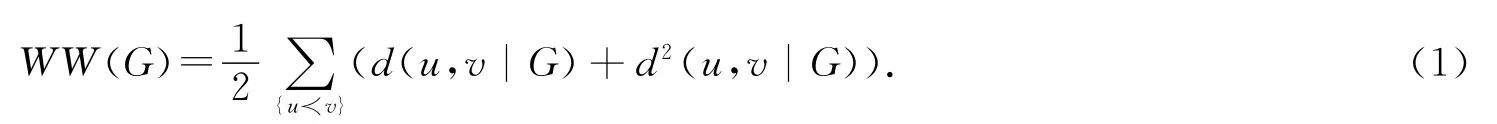
Bo Zhou［5］提出了hyper－Wiener指标的另一计算式.令d（G，k）表示图G 中距离为k 的无序点对的个数，则图G 的hyper－Wiener指标为

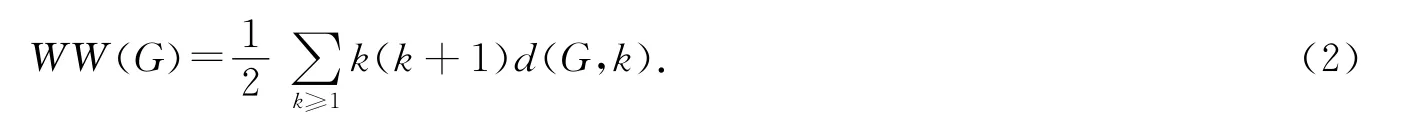
令G＝（V，E）表示顶点数｜V（G）｜＝n，边数｜E（G）｜＝m 的连通图.若m＝n＋c－1，则G 被称为c－圈图.特别地如果c＝1，则图G 称为单圈图.Kn，Pn与K1，n－1分别表示n阶完全图，路及星.图G 中不邻接的2条边称为是独立的.两两独立的边构成的集合称为图G 的一个匹配.如果图G 的所有顶点都包含在一个匹配中，则称这个匹配为图G 的一个完美匹配.

文献［4－8］研究了树的hyper－Wiener指标，因此有必要对非Kn的c－圈图的hyper－Wiener指标做进一步研究.

猜想1：设完美匹配c－圈图G（n，m）为取得最小hyper－Wiener指标的极图，则G 不包含P5且必有一顶点u度数为

令U3（s1，s2，s3）表示由3个顶点极小圈C3＝r1r2r3r1和粘在极小圈顶点ri上的悬挂树Tri构成的单圈图.其中｜V（Tri）｜＝si表示悬挂树Tri顶点个数.引理1—3在文献［9－10］中已给出证明：

引理1 设U3（s1，s2，s3），U3（s1＋s2，0，s3）及U3（s1＋s2＋s3，0，0）为如上定义单圈图，则

引理2 设G 和G′为由子图A，B 和路Ps＝p1p2…ps（s≥2）构成的n 阶简单连通图（图1），则WW（G）＞WW（G′）.

引理3 设H 和H′为如上所定义的n 阶连通图（图1），则当n≥5时，WW（H）≥WW（H′），等号成立当且仅当｜V（A）｜＝2.

令U＋（2n）表示2n阶完美匹配单圈图的集合.设Uk（2n）为u＋（2n）中由k个顶点极小圈Ck＝r1r2…rkr1和粘在极小圈顶点ri上的悬挂树Tri构成的单圈图.若边e＝uv为悬挂树上一条非悬挂边，施行图形变换Ⅰ：收缩边e＝uv为顶点u，在顶点u上增加一条悬挂边uu′；否则施行图形变换Ⅱ：收缩边uv 和边u1u 到顶点u1，在顶点u1上增加长为2的路u1u′v′（图1），最终得到单圈图（t1，t2，…，tk）（图2）.

图1 引理2中的图G 和G′与引理3的图H 和H′Fig.1 Graphs Gand G′in Lemma 2，Hand H′in Lemma 3

推论1 设Uk（2n）和（t1，t2，…，tk）为如上所定义的完美匹配单圈图，则

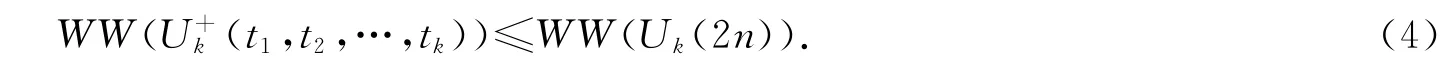
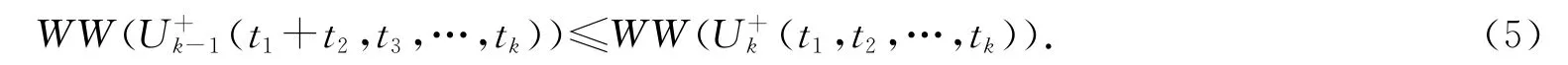
证明 将连通图G＝（V，E）的顶点集分为3部分，e＝uv为连通图G 的一条边，

设x∈Nr2（e）－｛r2｝且y∈V（Tr2）－｛r2｝，下列等式成立：

情形1：k为偶数，设顶点x，y∈V（U＋k）－｛r1，r2｝，显然

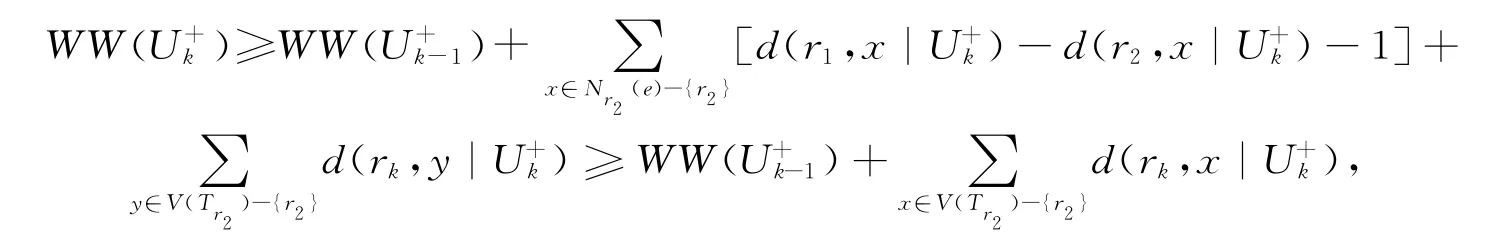
等号成立当且仅当k＝4且t1＝t2＝｜V（Trk）｜＝0.

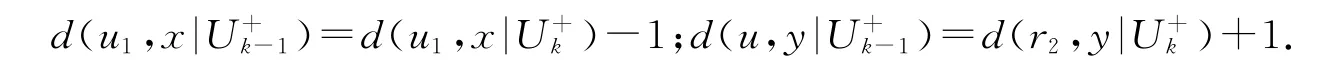
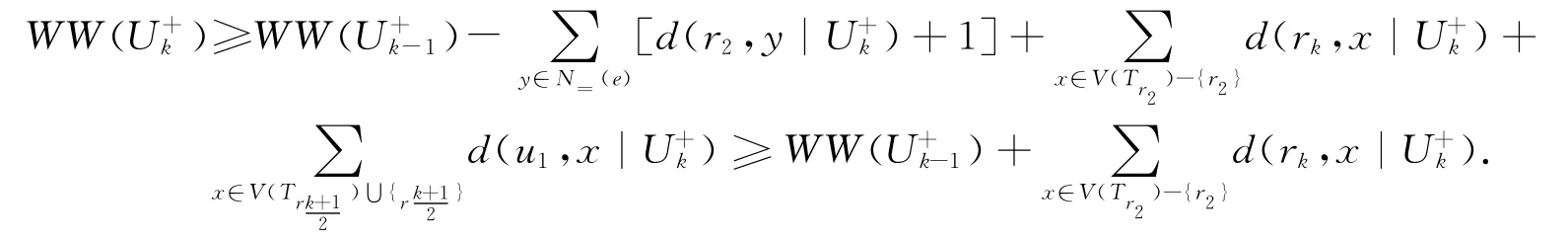
等号成立当且仅当k＝5且t1＝t2＝｜V（Trk）｜＝0.证毕.

图2 图形变换Ⅳ与ⅤFig.2 Graph transformationⅣandⅤ

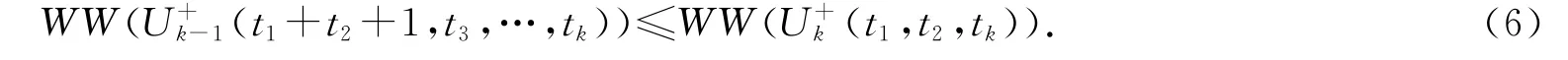
证明 设x∈Nr2（e）－｛r2｝且y∈V（Tr2）－｛r2，｝，下列等式成立：

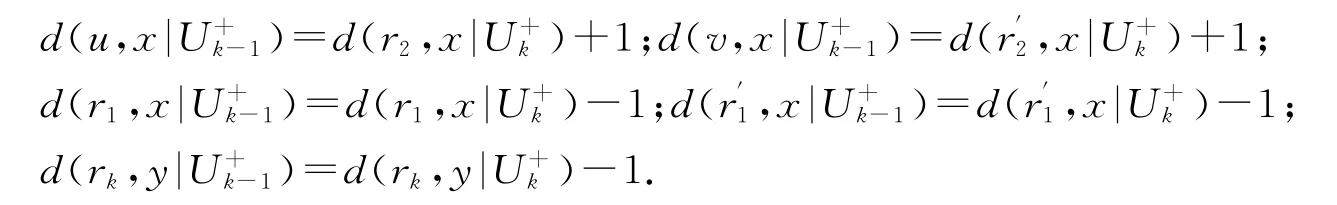
情形3：k为偶数，显然N＝（e）是空集.设顶点x，y∈V（t1，t2，…，tk））－｛r1，r2｝，显然d（x，y｜

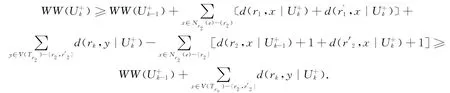
等号成立当且仅当k＝4且t1＝t2＝｜V（Trk）｜＝0.

等号成立当且仅当k＝5且t1＝1，t2＝｜V（Trk）｜＝0.证毕.

设边e＝r1r2为圈Ck上的一条边，若顶点r1和r2上都没有悬挂边，对边r1r2施行图形变换Ⅳ（图2）；若顶点r1，r2上各有一个悬挂边，对边r1r2施行图形变换Ⅴ（图2）.

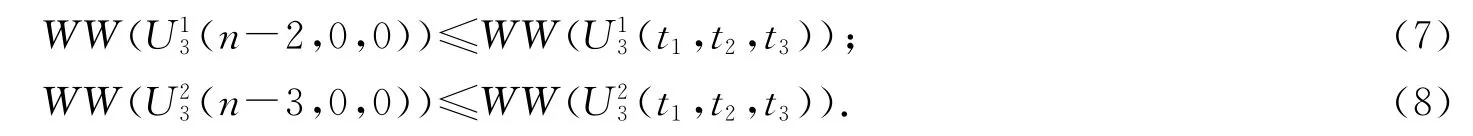
证明 由图形变换Ⅲ及引理3可知，不等式（8）显然成立.由等式（2）可知

不妨假设t1≠0且证毕.

定理1 设G∈u＋（2n）（n＞4），则

图3 图（t1，t2，t3）与（t1，t2，t3）Fig.3 Graphs （t1，t2，t3）and（t1，t2，t3）

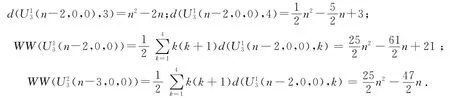
［1］ DOBRYNIN A A，GUTMAN I，KLAVZAR S，et al.Wiener index of hexagonal systems［J］.Acta Appl Math，2002，72：247－294.

［2］ KLAVZAR S，ZIGERT P，GUTMAN I.An algorithm for the calculation of the hyper－Wiener index of benzenoid hydrocarbons［J］.Comput Chem，2000，24：299－233.

［3］ KLEIN D J，LUKOVITS I.On the definition of the hyper－Wiener index for cyclecontaining structures［J］.J Chem Inf Comput Sci，1995，35：50－52.

［4］ GUTMAN I.Relation between hyper－Wiener and Winer index［J］.Chem Phys Lett，2002，364：352－356.

［5］ ZHOU Bo，GUTMAN I.Relations between Wiener，hyper－Wiener and Zagreb indices［J］.Chem Phys Lett，2004，394：93－95.

［6］ KHALIFEH M H，YOUSEFI－AZARI H，ASHRAFI A R.The hyper－Wiener index of graph operations［J］.Comput Math Appl，2008，56：1402－1407.

［7］ WIENER H.Structural determination of paraffin boiling points［J］.J Amer Chem Soc，1947，69：17－20.

［8］ CASH G G.Polynomial expressions for the hyper－Wiener index of extended hydrocarbon networks［J］.Chem，2001，25：577－582.

［9］ 侯远.单圈图的hyper－Wiener指标［J］.数学研究，2013，46：142－150.HOU Yuan.On the hyper－Wiener index of unicyclic graphs［J］.Journal of mahthematical study，2013，46：142－150.

［10］ 侯远.完美匹配树的hyper－Wiener指标［J］.闽江学院学报，2013，34：10－12.HOU Yuan.Minimum hyper－Wiener index of trees with perfect matchings［J］.Journal of Minjiang University，2013，34：10－12.