一种采用泛进制计算法进行求解密钥的方法

杨 虹

（辽宁警察学院 辽宁 116036）

0 引言

当前，世界计算机领域都在努力探索更加安全的数据保护方法，因此产生了很多加密解密算法。其中主要有两大阵营，一是DES加密方法，称为对称加密方法；二是非线性加密解密方法，即以公式为主要计算方法。DES方法没有可利用的公式，要想破解，需要采用穷举法；非线性加密解密方法通过公式求解密钥，最大特点是不可逆，其中以RSA算法和椭圆曲线算法为典型计算方法。

此外还有很多加密解密方法，虽然没有公开（即被破解），但其中的原理基本相同。为了提高加密解密的难度，通常采用DES与非线性加密解密两种方法的组合，以达到不被破解的目的。

1 RSA算法与椭圆曲线算法概述

1.1 RSA算法

RSA算法是一种非对称密钥算法。所谓非对称就是指该算法需要一对密钥，其中一个用于加密，另一个用于解密。

RSA算法涉及3个参数：n、e1、e2。其中，n是两个大质数p、q的积。n是二进制表示所占用的位数，即密钥的长度。e1和e2是一对相关的值，e1可以任意取值，但要求e1与（p-1）*（q-1）互质；再选择e2，要求（e2*e1）mod（（p-1）*（q-1））=1。

（n 及e1），（n及e2）就是密钥对。

RSA的加密算法和解密算法完全相同。设A为明文，B为密文，则：

e1和e2可以互换使用，即：

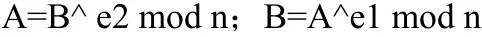
以上就是RSA算法。

1.2 椭圆曲线算法

椭圆曲线理论是代数几何、数论等多个数学分支的一个交叉点，一直被认为是纯理论学科。近年来，由于公钥密码学的产生与发展，该学科也找到了它的应用领域。在 RSA 密码体制的基础性问题——大整数分解和素性检测——的研究方面，椭圆曲线是一个强有力的工具。特别以椭圆曲线上的（有理）点构成的 Abel 群为背景结构，实现各种密码体制已是公钥密

码学领域的一个重要课题。由于椭圆曲线密码体制本身的优点，自20世纪80年代中期被引入以来，椭圆曲线密码体制逐步成为一个十分令人感兴趣的密码学分支，1997年以来形成了一个研究热点，特别是移动通信安全方面的应用更是加快了这一趋势。

椭圆曲线算法是在有限域Fp约束下，其中p为一个大质数，椭圆曲线可定义成所有满足方程式E：y2=x3+ax+b（x，y，a，b∈F）的点（x，y）所构成的集合。若方程式x3+ax+b没有重复因式或4 a3+27 b2≠0，则E：y2=x3+ax+b 能成为群。定义：

（1）椭圆曲线中存在一个无限远的点O，但它并不在椭圆曲线上。

（2）若P 的负点称为−P，则点P=（x，y）相对X坐标轴反射的点为−P=（x，−y）。

（3）若椭圆曲线上点P 的域为n，则n是最小的使得nP=0的正整数。

（4）椭圆曲线上的运算结果可以生成椭圆曲线上的所有点，但点O除外。

（5）E（Fp）为在Fp之下，由椭圆曲线E上全部点所构成的集合。

（6）若有两个点P=（x1，y1）∈E（Fp）及Q=（x2，y2）∈E（Fp），且P≠±Q，则P+Q=R=（x3，y3）。其中，X3=（（y2-y1）/（x2-x1））2-x2-x1’，Y3=（（y2-y1）/（x2-x1））（x1-x3）-y1。

（7）若有两个点 P=（x1，y1）∈E（Fp）且 P≠-P，则 P+P=2P=（x3，y3），其中，X3=（（3x12+a）/2y1）2-2x1，Y3=（（3x12+a）/2y1）（x1-x3）-y1。

（8）若对所有点（Fp）P∈E，则P+O=O+P=P、P+（−P）=O、O=−O。

（9）分配律成立，即若n∈F，则（m+n）P=mP+nP。

（10）交换律成立，即若pm，n∈F，则m（nP）=mn（P），其中kP=P+...+P。

以上就是椭圆曲线算法。

1.3 两种算法总结

这两种算法的特点如下：

（1）都需要求出两个或两个以上的未知数作为密钥。

（2）公式可以重复使用。

（3）用素数做模进行计算。

（4）计算较复杂。

（5）不可逆运算。

由此得出结论，如果能找到一种算法具备以下特点，这个算法将会更加实用、有效：

（1）能够求出两个以上未知数。

（2）公式可以重复使用并简单。

（3）用计算机里的数据（或任意整数）能求解出密钥或多个密钥。

（4）计算简单，为不可逆运算。

（5）提高在计算机中的运算速度。

2 泛进制算法及三参数建立方法

2.1 泛进制算法

将任意进制数N转换成十进制数的方法为：N=10s+m。式中，10表示十进制；s表示10的倍数；m是余数。

由此可见，将任意进制整数N转换成所需要的某进制整数，可以写成：

其中，N是范围为 0，1，2，3，……的任意进制整数；p是范围为2，3，……的任意整数；s是p的倍数，表示范围为0，1，2，3，……的任意整数；m是余数，范围为0，1，……p-1，该值与p有关。

例如，一个十进制数为254，选定p=14，根据公式（1），得到s=18，m=2。

如果选定p=15，根据公式（1），得到s=16，m=14。

通过改变p的值，可以得到不同的s、m的值。

如果上式中的p可以任意选定，那么公式（1）可以表示任意进制转换的数。由于公式（1）中有3个未知数（3个变量），且这3个未知数可以变化，恰好符合计算机密钥的变化规律，因此这3个未知数可以作为密钥。

数字被p、s、m 三个因子所分解，每个因子所表达的含义与原数字（或代码）所表达的含义完全不同，即改变了原数字。

知道p、s、m三个参数中的一个或两个参数，都不能求出原数据，符合非对称加密特点。由于公式简单，所以计算速度较快。

例如，一个十进制数为200，令p=13，利用公式（1）经过计算得到N=13×15﹢5。

其中，p=13，s=15，m=5。由此可见，数字 200完全变形为三个因子13、15和5。

这种算法的特点是密钥的计算方法简单，且采用的进制数越大，被解密的可能就越小。

2.2 三参数建立方法

由公式（1）计算出三个参数p、s、m，将三个参数分别代入x、y、z坐标中，数字N可记做N（x、y、z），根据x、y、z坐标点，将数字隐藏到三维坐标表示的点内，形成三维加密方法。

因为计算公式简单，容易被破解。在加密算法中，采用如此简单的公式并不多见。一个数据用三维坐标表示，或多维坐标表示，其解密难度呈非线性增长。因此每增加一维参数，对解密工作者需要千百万次穷举法才能破解，所以增加破解难度。按照这个思路，还可以将数字N用更多维进行表述。利用多参数变化，也能达到加密目的。

3 泛进制算法特点

3.1 计算简单

由公式（1）可以看出计算公式的参数非常简单，比任何非线性加密解密计算方法都简单。不仅如此，采用公式（1）进行迭代运算，也可以获得多个参数。其他非线性加密方法采用迭代法，会影响计算机运行速度，而泛进制计算方法不会影响计算机中该算法的运行速度。

通过增加参数降低数学公式的运算难度，这是非线性加密解密最好的解决问题方法。不仅避免了许多深奥的数学计算和数学变化，还达到了不可逆计算的目的。

3.2 破解难度大

实际应用中，公式（1）中参数是可以选择的。根据需要，一般把p选择得大一些，这样可以增加破解难度。由于公式（1）对三个参数表示范围进行了界定，且这三个参数的取值范围与其在计算机中所需存储单元的位数有关，即若公式（1）中参数p的位数为xp，参数s的位数为xs，参数m的位数为xm，令xp=w，xs=y，xm=z，则理论上公式（1）中参数（即密钥）有2w×2y×2z种可能，所以，采用穷举法很难进行破解。

3.3 易于编程实现

每种加密解密方法都需要通过计算机编程得到密钥，编程难度与程序是否容易实现相关。可以看出，公式（1）无论用什么语言编程都很容易实现，因为在计算机语言中，都有除法运算语句（指令），只要选定公式（1）中的p值，就很容易计算出s和m值。

3.4 p值选定具有随机性

公式（1）中的p值选定非常关键。p值不能固定不变，如果p值固定不变，将会导致破解难度降低。计算机中的数字本身就是随机的。利用计算机数字的特点，将一个数字分解成两组数据，如果将某组数据作为p值，即指定计算机里某几位数字作为p值，s和m的值就很容易求出。

前面已经定义公式（1）三个参数的取值范围，根据需要还可以采用超范围定义方法定义泛进制参数，将数字N中某参数取负值，同样也可以得到数字N。具体计算方法如下：

令数字N为正整数，N=ps+m，取p为负数，则p写成-p，即N=-ps+m，得m=（N+ps），所以，出现m大于N值显现；同理可以得出很多结果，如果把三维坐标分成8个象限，一个数字N，就会有8个三维坐标象限表示的数组，因此解密难度远远大于两维坐标表示的4象限数组。

3.5 计算方法具有可迭代性

公式（1）代入p，则有：

公式（1）代入s，则有：

公式（1）代入m，则有：

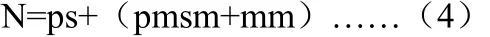
公式（1）分别代入p，s和m，则有：

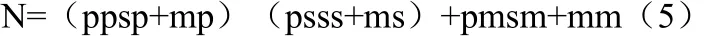
公式（1）还可以继续代入 pp，sp，mp……，即可得到更多参数（或密钥）。

3.6 解决非线性密钥生成困难的问题

由RSA算法与椭圆曲线算法可以看出，虽然椭圆曲线算法比RSA算法简单，但非线性密钥生成却是很复杂的。计算机信息安全技术人员一直在寻找简单且行之有效的密钥生成方法。那么，密钥变化主要与哪些因素有关呢？一是未知数变量有多少，即密钥有多少。未知变量的增加实际就是密钥的增加。在加密过程中，采用哪几个密钥进行加密，哪些密钥不参与加密，只有加密人员根据迭代计算基本公式（1）选取参数的合理性而定，所以破解起来非常繁琐，不易成功；二是随机性，即在加密过程中参数需要随机选定，这样有利于加密，起到增加破解难度的目的；三是对称加密与非对称加密方法的结合。若p值固定，即是对称加密方法；四是整数求解公式的表达完整性。该迭代计算公式只适用于整数计算，因此加密计算简单、方便。只要满足上述条件，加密会变得相对简单，而解密则变得相对复杂。

3.7 泛进制与RSA及椭圆曲线加密算法比较

泛进制计算方法与RSA和椭圆曲线加密算法比较，泛进制计算简单，有三个以上参数；而RSA和椭圆曲线加密算法计算公式比泛进制算法复杂，只有两个参数。

泛进制计算方法可以迭代，而RSA和椭圆曲线加密计算不适合多次迭代，其原因是RSA和椭圆曲线加密计算复杂，如果再次迭代，速度会更慢，显然不适合反复迭代。

泛进制加密方法可以实现三维空间数据加密，这种运算方法决定加密数据是存放在三维坐标之中的，因此三维数据隐藏方式要比二维隐藏方法要有难度，而泛进制很好的避开三位加密运算复杂的问题，很容易得到三维坐标点，所以采用泛进制加密方法为今后加密指出另一条加密思路。

4 结束语

泛进制加密方法是一种非线性的多密钥计算方法，解决了非线性计算复杂的问题，同时可以大大地提高其在计算机中的处理速度，能实现三维空间加密，利用公式（1），还能进行迭代扩展。在RSA加密和椭圆曲线加密中的密钥，计算公式很复杂，只能获得两个密钥。相比较而言，采用泛进制加密方法的多密钥计算公式求解方法方便、简单、实用，是一个较理想加密解密算法。

[1]李宁.基于正规基的椭圆曲线密码算法的研究和IP核实现[D].西安电子科技大学.2010.

[2]陆志彬.浅析椭圆曲线密码系统的应用原理[J].计算机光盘软件与应用.2010.

[3]程华.一种基于构造法的椭圆曲线改进算法[J].网络安全技术与应用.2009.

[4]张京京，闫晓蔚，蔡建顺，郭曙光.基于 Android系统的手机隐私安全的研究与实现[J].信息网络安全.2012.

[5]庞辽军，李慧€贤，裴庆祺，柳毅，王育民.一个单方加密-多方解密的公钥加密方案[J].计算机学报.2012.

[6]黄东伟.移动可编程数据加密系统的设计与实现[D].青岛科技大学.2010.

[7]符浩，陈灵科，郭鑫.基于Web网络安全和统一身份认证中的数据加密技术[J].软件导刊.2011.

[8]杨义先，钮心忻.应用密码学[M].北京邮电大学出版社.2005

[9]章照止.现代密码学基础[M].北京邮电大学出版社.2004.

[10]许春香，李发根，聂旭云，禹勇.现代密码学[M].电子科技大学出版社.