拟牛顿算法收敛性证明中的几个定理
牛潇萌
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
拟牛顿算法收敛性证明中的几个定理
牛潇萌
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
互补问题是一类重要的优化问题,它在工程、经济和交通平衡等领域都有重要应用.本文给出了非线性互补问题的光滑化拟牛顿算法,并给出证明此算法全局收敛性的几个重要定理.
非线性互补问题;拟牛顿;光滑函数
1 非线性互补问题光滑化拟牛顿算法
考虑P0函数非线性互补问题:求x∈R0,使得

其中F是连续可微的P0函数.
使用如下光滑函数[1]:

其中ø(μ,a,b)∈R3.
设z=(μ,x)∈Rn+1,

其中

经简单计算易知H(z)的Jacobian矩阵为

其中

且

易知对所有i=1,2,…,n有
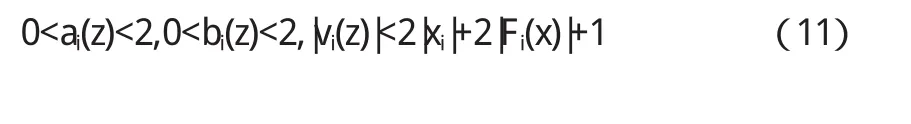
设γ∈(0,1).定义函数ρ:Rn+1→R+为
算法1[2](光滑化拟牛顿算法)

选一个初始非奇异矩阵B0∈Rn×n.设k=0.
步1若||H(zk)||=0,停.否则,设ρk:=ρ(zk).若μk>ρkμ0,解下面的方程得

否则,令Δzk=(Δμk,Δxk):=(0,Δxk),并解如下方程组得Δxk,

其中Gk∈R(n+1)×(n+1)定义为

且Bk是▽xΦ(zk)T的一个近似.
步2 若

则设λk:=1,转步4.
步3 设λk是取自集合{1,δ,δ2,L}使得λ=δi满足如下线搜索的最大数

步5用如下Broyden-like校正公式修正Bk得Bk+1:
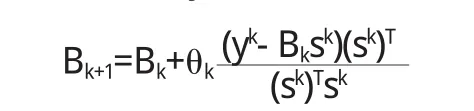
步6令k=k+1,转步1.
定理1[2]算法是有定义的,且产生一无穷序列{zk=(μk, xk)}满足{(μk)}⊂R++是单调非增的.
2 非线性互补问题光滑化拟牛顿算法收敛性证明中的几个重要定理的证明
设

定理2[3]设μ>0且ø:R++×R2由 (18)定义.设{ak},{bk}是满足下列条件的两个序列ak,bk→+∞或ak→-∞或bk→-∞.则对任意(μ,a,b)∈R++×R2,有

定理3假设F是连续可微的P0函数,H(z)由(3)定义,}由算法1产生.令>0,如果对所有的k≥0有μk≥且那么

证明 由定理1知{μk}单调非增,从而对任意k≥0,有.用反证法证明,假设存在一无界序列{xk},使得||H(μk,xk)||有界.因为序列{xk}是无界的,所以指标集I:={i∈N: {xik}是无界的}是非空的.不失一般性,可假设{|xjk|}→+∞,∀j∈I.定义序列}为


其中j是取得max的指标之一,不失一般性,假设j与k是相互独立的.因为j∈I,所以

现考虑下面两种情况:

因此由(2),(4)和定理2可得

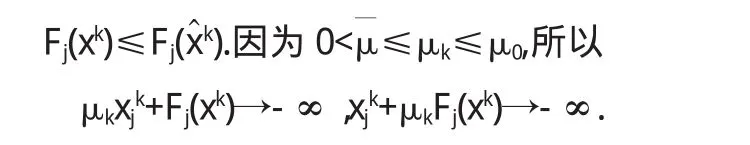
因此由(2),(4)和定理2可得

证明 由(16),(17)可知对所有k,||H(zk+1)||≤(1+ηk)||H (zk)||,从而

所以xk+1∈Lμk+1.
定理5设{zk}由算法1产生,则

证明 由(16),(17)可知对所有k有
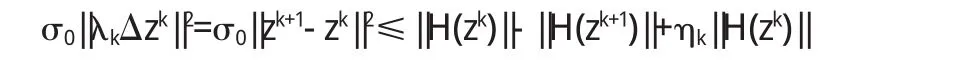
其中σ0=max{σ1,σ2},所以
整个丧礼,桃花像个木头人,人家叫她怎么做,她就怎么做;只有一件事她做不了,那就是哭丧。自始至终,桃花都没有哭过。人们对她说话,她充耳不闻,她也不说话,就连儿子黄方永哭着喊着叫她妈妈,她也不理不睬的。事后,人们担心的事还是发生了;桃花常常忘了回家,确切地说,是找不到家,一个人在田野上瞎走,嘴上喃喃自语:“回去吧!回去……”大家都说桃花丢了魂。黄石、黄羊和黄鹿不得不去把她找回来。而桃花突然清醒过来,是有一天她在田里劳动时,被体内的脚踢了一下;她愣住了,直起身来,轻轻地抚摸肚子;忽然又一脚,她苍白的脸才一点点地活动起来,就有了活物的神色。

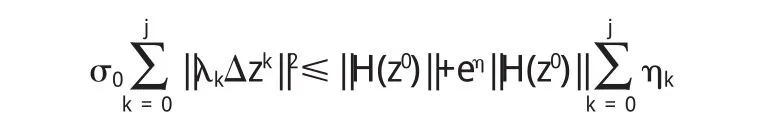
令j→∞且由(12)可得,
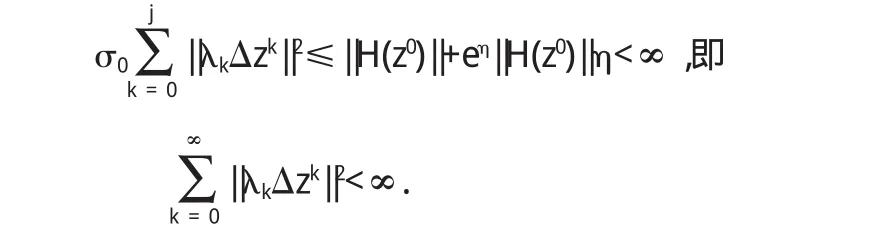
引理1[4]设{ak},{tk}是满足如下条件的正数列ak+1≤,则}收敛.
定理6设{zk}由算法1产生,则序列{||H(zk)||}收敛.
引理2[5]如果F:D⊂Rn→Rn在凸集D0⊂D上是可微的且对所有x∈D0,||F'(x)||≤M<+∞,那么F在D0上是Lipschitz连续的.
引理3[6]假设F是连续可微的P0函数且Φ(μ,x)由(4)定义.对任意μ>0和c>0,定义水平集Lμ(c):={x∈Rn:||Φ(μ,x) ||≤c},则对任意μ2≥μ1>0,集合是有界的.特别地,对任意μ>0和c>0,集合Lμ(c)是有界的.

定理7假设F是连续可微的P0函数且F'(x)在集合L)是Lipschitz连续的,其中Lμ(c):={x∈Rn:||Φ(μ,由(6)定义,则存在使得

证明 由(6)可知

由(11)知

由L(c)定义和引理3知μ,μ'∈[μ1,μ2],x,x'有界.又因为F'连续,所以F'(x')有界.故证明(24)成立,只需证明存在正常数L1,L2,L3,L4,使得
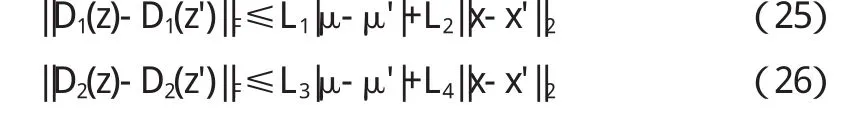
下面只证明(25),(26)类似可证.为证(25)只需证明存在0,使得



为证明简便引入如下记号:是有界的,不妨设其界分别为M1,M2,M3,则

同理

由L(c)的有界性和F'的连续性知F'在L(c)上是有界的,所以由(28)—(30)以及引理2知(27)成立.
由L(c)的有界性和F的连续性知F在L(c)上有界,从而
〔1〕Z.Huang,J.Han,D.Xu,L.Zhang,The non-interior continuation methods for solving the -function nonlinear complementarity problem [J].Science in China, 2001,44:1107-1114.
〔2〕牛潇萌.非线性互补问题的光滑化拟牛顿算法[J].计算机工程与应用,2013,49(18):33-35.
〔3〕C.F.Ma,L.J.Chen,D.S.W ang,A globally and superlinearly convergent smoothing Broyden-like method for solving nonlinear complementarity problem[J].Applied Mathematics and Computation,2008,198:592-604.
〔4〕D.H.Li,M.Fukushima,A derivative-free line search and global connvergence of Broyden-like method for nonlinear equations[J].Optim ization Methods and Software,2000,13:181-201.
〔5〕J.M.O rtega,W.C.Rheinboldt,Iterative solution of nonlinear Equations in several Variables[M].New York, Academic press,1970.
〔6〕L.P.Zhang,J.Y.Han,Z.H.Huang,Superlinear/ Quadratic one-step smoothing New ton method for-NCP[J].Acta Mathematica Sinica,2005,21:117-128.
0224
A
1673-260X(2014)03-0001-03

