微孔洞缺陷岩石轴压下弹塑脆性模型损伤研究

宋 力，魏赛平，谷 麟，樊 成

（大连大学 材料破坏力学数值试验研究中心，辽宁 大连 116622）

工程岩体从力学上看，与其他工程材料的主要差别在于它的不连续性、不均匀性和多裂隙性，常常分布大量的裂纹和孔洞等缺陷。因此，造成了实验室获得的有关岩石试样的力学性能、参数和破坏规律不能直接用于工程岩体。集网格生成、数值计算和相关图形生成于一体的非均质材料的弹塑性破裂过程数值模拟程序REPFPA，可以对岩石试样和工程岩体的弹塑性破裂过程进行数值模拟［1］。岩石作为一种经历了漫长的地质构造作用并隐含了复杂的应力、变形及损伤历史的地质体，其内部存在着大量的微细裂纹和微孔洞等缺陷［2］，这些大小不等、位置随机的微孔洞缺陷的存在，改变了岩石的力学性能，降低了岩石的极限承载能力。因此开展含孔洞缺陷介质破坏行为的研究，具有重要的学术和工程意义。

在研究工程岩体的变形特征和破坏规律时，试验研究和数值模拟方法均是非常有效的研究方法。目前国内已有很多学者在岩石及岩体损伤与断裂、破裂过程数值模拟等研究方面取得了很多成果［3－8］。对于这三者之间的联系与差别以及造成这些差别的原因的研究则尚显得不足。基于此，本文将关于弹塑脆性岩石变形破坏的损伤力学、数值模拟及实验室试验的研究结合起来，来对比研究它们之间的联系与差别。

本文采用自主研发的弹塑性有限元计算程序REPFPA［9－11］，采用细观单元的弹塑脆性本构关系，考虑材料的非均质性、各向异性和多裂隙性（本文主要研究探讨微孔洞缺陷对性能的影响），建立了基于细观力学的弹塑脆性损伤模型，分别研究了不同微孔洞对岩石单轴压缩荷载下的细观弹塑性损伤破坏行为的影响，通过将有限元计算结果与物理实验［12］数据进行分析验证，得出微孔洞缺陷对岩块破坏情况的一般规律。

1 细观单元的本构关系

本文从材料的细观层次出发，针对岩石材料拉压强度不同的特性，分别采用基于应力空间下的最大压应力失效准则和应变空间下的极限等效塑性应变失效准则，建立了一个具有应变硬化的弹塑脆性本构模型。如图1所示，A点是弹性阶段进入塑性阶段的标志，该点由屈服准则决定；B点是塑性强化阶段到单元失效的标志，该点由失效准则决定；C点是材料进入残余屈服面阶段的标志，由残余强度确定。

图1 细观单元本构模型Fig.1 Constitutive model of mesoscopic element

1.1 屈服准则和应变硬化

对于岩石材料基于应力空间的屈服问题，目前在工程中应用较好的有D－P准则、M－C准则等。

屈服后的应变硬化，本文采用线性强化模型，其中强化参数H′可由简单的单向屈服试验来确定。

式中，dε—总应变增量；dεe—弹性应变增量；dεp—塑性应变增量；E—材料的弹性模量；ET—材料屈服后的切线弹性模量。

1.2 材料的失效

一般岩石材料的破坏可区分为剪切破坏和压缩破坏。由于岩石材料的抗拉强度远低于抗压强度，本文假定的压缩破坏为弹塑脆性破坏，材料破坏后有残余强度σr。

另一方面，本文认为岩石材料的剪切破坏发生在屈服以后，屈服是由于裂隙面的滑移所造成，因此必然存在塑性变形。这里认为材料失效后承担一定的残余力。

材料在发生屈服后，应力—应变关系具有明显的非线性，仅通过应力判断材料发生卸载或是软化存在局限性，由于塑性应变作为内变量可体现加载路径和加载历史，所以在应变空间下建立材料屈服后的破坏准则是必要的。本文采用等效塑性应变来描述材料屈服后的塑性程度，即

1.3 单元失效的数值实现

材料失效后，应力的跌落是由于单元的刚度因失效而降低产生的，其中总变形和塑性变形都不变。本文分别对基于等效塑性应变的拉伸损伤变量和压缩损伤变量进行定义

式中，ωt—拉伸损伤值；ωc—压缩损伤值；—当前材料单元的总塑性应变张量；εkl—当前材料单元的总应变张量，—四阶弹性刚度张量各分量。

当应力跌落完成后，在残余的塑性屈服面上将发生塑性流动。对于未发生单元失效的塑性屈服准则，其后继屈服面的形状通常保持不变，而在失效单元发生应力降低后，材料的残余屈服面的形状和面积都将发生变化。材料在破坏后存在一定的残余强度，通常表现为黏聚力和摩擦力的降低，即为折减后的cr和φr。

2 细观骨料模型的建立

岩石材料的不均匀性、不连续性和材料参数分布的离散性和随机性是岩石弹性模量和强度的重要影响因素［13］。为了全面地反映岩石存在的这些特性，本文从材料的细观层次出发，考虑材料非均质性，讨论含单孔洞缺陷试样在受压状态下，裂纹扩展和破坏变形的特点以及其与强度的关系。本文考察改变孔洞缺陷试样的尺寸（主要是试样的宽度）的直径，固定孔的直径。

为了描述岩石材料性质的非均匀性，其各相材

式中：ci—统计函数的标准化常数；mi—统计函数的形态参数，在此表征为非均匀性材料；下标i为材料参数号（不代表求和），共有9个参数表征岩石力学性质，参数的选取详见表1。当i＝1时，描述的是材料的弹性模量E的概率密度，这时σi代表E，而σi0表示为此材料参数的统计平均值。料的力学参数应具有一定的随机性。本文假定组成材料细观单元的力学性质满足 Weibull分布规律，其概率密度函数可以统一写为

表1 材料参数Table 1 Material parameters

通过蒙特卡罗方法将这些随机变量逐一赋值到各单元中，这些单元体材料参数既符合统计分布规律，又具有随机性，能很好地体现出岩石介质的材料特性。

3 孔洞对试样裂纹扩展的影响

本文采用如图2所示的模型进行单轴受压预置孔洞缺陷试样的破坏过程分析，试样尺寸长L，宽W，厚度取一个单位，居中的孔洞缺陷直径为d，本文研究L＝24.0mm，d＝1.5mm，W ＝3.0、5.0、7.0mm变化时的受拉破坏过程及其尺寸效应影响。采用平面应变分析，模拟过程采用竖向位移加载，直到岩石试样失稳为止。材料参数见表1。

图3～5分别是含有不同直径的单孔洞缺陷试样的数值模拟的整个过程演化图，在每个小图的下面标明了对应的加载应变。在初始状态，试样中除了预置的孔洞缺陷和本身固有的微缺陷及材料的非均质性，试样内部没有其它微孔洞和微裂纹。

随着应变的增大，孔洞周边开始萌生裂纹和扩展，裂纹开始沿孔洞顶部底部向轴方向扩展，孔洞缺陷周边这种裂纹扩展导致岩块试样的局部化破坏和新裂纹的形成，当试样宽度较小时，孔洞缺陷周边的主要扩展裂纹会沿着几乎平行加载方向发展直到试样发生劈破坏，随着宽度增加时，这种破坏慢慢发展为剪切破坏，这与物理实验［12］基本吻合。在单轴压缩作用下，裂纹的不同扩展形态导致不同的破坏行为。当应变增加，随着宽度的增加，裂纹出现时间会推迟，也就是说，在试样宽度较小的情况下，相同直径孔洞缺陷试样的裂纹更容易扩展。

图2 预置孔洞缺陷的岩块试样Fig.2 The rock specimens of preset hole defects

图3 尺寸3mm×24mm孔洞尺寸d＝1.5mmFig.3 Size 3mm×24mm defects size d＝1.5mm

图4 尺寸5mm×24mm孔洞尺寸d＝1.5mmFig.4 Size 5mm ×24mm defects size d＝1.5mm

图5 尺寸7mm×24mm孔洞尺寸d＝1.5mmFig.5 Size 7mm ×24mm defects size d＝1.5mm

4 非均质度对岩石破裂损伤的研究

取长L＝24.0mm，宽W＝5.0mm，直径d＝1.5mm，划分为4 300个单元，每个单元为8个高斯节点，考虑材料非均质度系数m的变化，取m＝3.0、10.0、100.0三种不同的均质度系数进行比较研究，假设岩块为平面应变状态，分析材料的破坏和均质度系数之间的关系。不同均质度系数预置孔洞缺陷试样单轴受压应变破坏曲线。

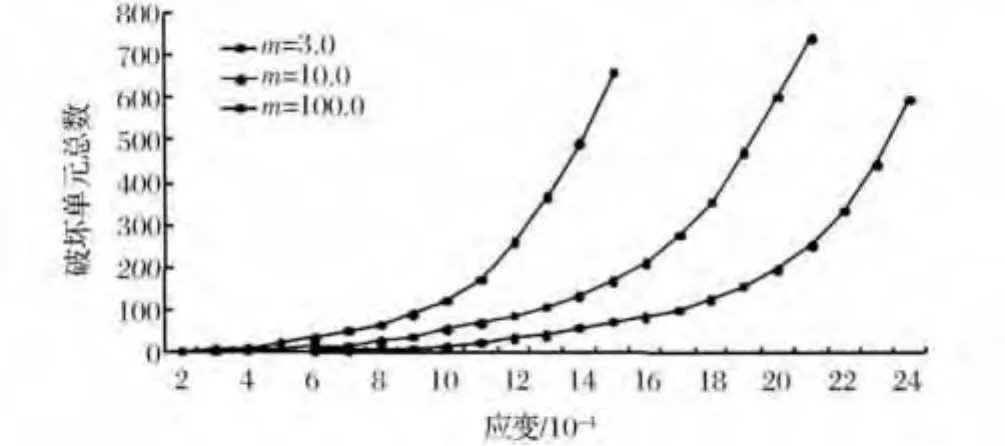
图6 不同均质度系数岩块试样应变破坏曲线Fig.6 The destruction strain curve of rock samples with different homogeneous degrees

由图6可得到如下规律：1）随着m的增加，即随着材料均质度系数的提高，岩块中破裂单元出现得晚，能承担的应变增大，稳定性增加；2）随着m的增大，岩块出现失稳即单元破裂数高峰来得晚，这使得工程岩体在开采时更需注意不同地质情况，针对不同地质情况，优化开采方案；3）随着m的增大，单元破裂出现得越来越晚，从出现破裂单元到岩块出现失稳的过程越来越集中，失稳变得越来越集中，这种失稳在工程上表现为岩爆，故对均质度系数比较大的岩体，岩体开始发生破坏时更应注意岩体失稳。

5 结论

建立了一个考虑材料的组成和非均质特性并具有弹塑性应变硬化的弹塑脆性本构模型，该模型在细观上，并基于有限元法进行了数值模拟。岩石试样在轴压下形成宏观损伤局部化带前，试件的屈服和破坏首先发生在孔洞缺陷边缘处的界面位置，并沿着界面扩展，贯通。从试验结果可以看出，孔洞顶部和底部所承受的应力应变最大，也最先发生破坏，并沿破坏区域逐步往约束边界发展，形成最终失稳破坏。

通过模拟考虑非均匀性岩石材料单轴受压预置孔洞裂纹试样的破坏过程，可以更真实有效地反应岩石材料的真实情况，通过非均匀性比较分析，能更真实有效地区分不同均质度岩体的破坏情况，为采矿工程、地下开挖等提供理论支持。

［1］ 肖丽萍，栾茂田，宋 力 .工程岩体弹塑性破裂过程数值模拟研究［D］.大连：大连理工大学，2004.

［2］ 徐 涛，唐春安，张 哲，等 .单轴压缩条件下脆性岩石变形破坏的理论、试验与数值模拟［J］.东北大学学报，2003，24（1）：87－90.

［3］ 谢和平 .分形—岩石力学导论［M］.北京：科学出版社，1997.

［4］ Xie H.Fractals in Rock Mechanics［M］.A A Balkema Publishers，Rotterdam.1993.

［5］ 谢和平 .岩石、混凝土损伤力学［M］.徐州：中国矿业大学出版社，1990.

［6］ 唐春安，徐小荷 .岩石声发射数值模拟中的几个关键问题［C］／／第三届全国青年岩石力学与工程学术讨论会文集 .成都：西南交通大学出版社，1995：1－7.

［7］ Tang C A.Numerical simulation of progressive rock failure and associated seismicity［J］.International Journal of Rock Mechanics and Mining Sciences，1997，34（2）：249－262.

［8］ Tang C A，Kaiser P K.Numerical simulation of cumulative damage and seismic energy release during brittle rock failure–Part I Fundamentals［J］.International Journal of Rock Mechanics and Mining Sciences，1998，35（2）：113－121.

［9］ 宋 力，林韵梅 .非匀质材料弹塑性破坏过程数值模拟研究［J］.力学与实践，2002（4）：30－32.

［10］ 宋 力，肖丽萍，林韵梅 .岩石弹塑性破裂过程的数值模拟研究［J］.力学学报，2005，37（4）：516－521.

［11］ 于永江，王大国，李 强，等 .煤岩体的弹塑脆性本构模型及其数值试验［J］.煤炭学报，2012，37（4）：585－589.

［12］ 林 鹏，唐春安 .含裂纹与孔洞缺陷介质的脆性破坏行为［D］.沈阳：东北大学，2002.

［13］ 宋 力，王大国，杨 阳，等 .细观力学的混凝土弹塑脆性损伤研究［J］.应用力学学报，2013，30（4）：480－487.