基于工业CT的轴类零件故障诊断

白 玉

（湖南省核工业超硬材料研究所，湖南 长沙 410007）

0 引言

轴类零件在粗加工之后需要热处理，在此过程中产生的残余内应力使得零件可能产生裂纹，此外，铸造过程中出现缩孔、夹渣也会导致零件出现片状裂纹。因此此类零件需要在粗加工之后进行磁粉探伤，防止零件失效，但磁粉探伤只适用于表面裂纹检测。针对该现象，仵彦卿等［1］采用工业CT扫描，得到起裂门槛值并且发现小裂纹的扩展规律，可见工业CT有助于进一步研究深埋裂纹。

1 轴式样的裂纹扩展预测流程

本文使用工业CT扫描，获得零件CT图像，再利用Canny算法提取该零件的边缘轮廓，然后矢量化其边缘，构造含有裂纹的有限元模型，运用K准则预测轴式样裂纹，具体流程如图1 所示。

1.1 工业CT扫描

在工业CT中，扫描时用线阵探测器的扇束射线扫描目标区域，对轴式样采用DR照相定位裂纹，扫描距离为1mm，图像大小为316×316像素，像素大小为0.315mm×0.315mm。取得11张含裂纹图像，观察分析这11张裂纹图像，轴式样内部裂纹为片状，如图2 所示。

1.2 提取轴式样边缘

Canny［2］算法具有好的信噪比，好的定位性能，对单一边缘仅有唯一响应的优点，所以采用该方法提取目标边缘。

1.3 边缘拟合

1.3.1 边缘跟踪

首先提取图像边界点，然后依次连接得到一条封闭连贯且完整的单像素边界轮廓线。本文跟踪轴式样轮廓时用Freeman［3］，中心像素的8个方向及链码的分布如图3 所示。跟踪从目标区域最左下方边界点开始扫描沿左上方向结束。链码检测的结果存放在数组List［m］［n］，后续工作中，依次按照表1中各链码序列解码成相应的X，Y坐标值即可。

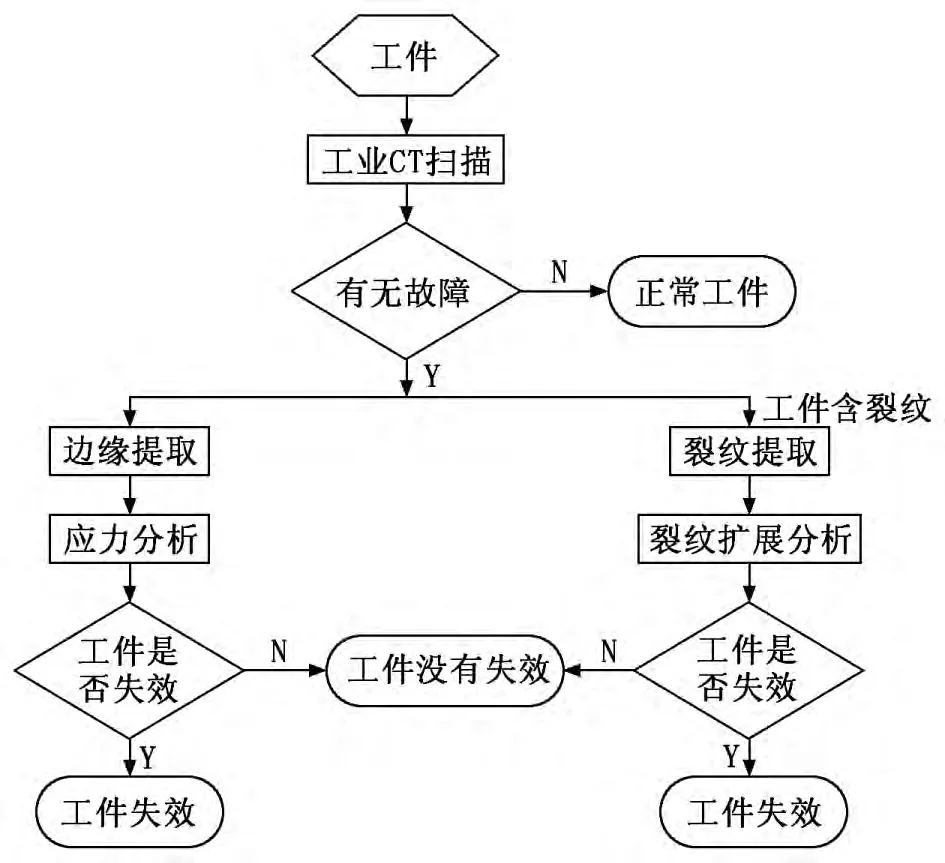
图1 轴式样的裂纹扩展预测流程

1.3.2 裂纹边缘拟合

直线拟合边缘是最基本的方法，该切片裂纹以片状的形式存在，且在切片上呈直线状，因此采用直线对裂纹进行拟合。边缘跟踪所得到的一系列封闭轮廓的边缘点个数记为N，分别构建数据链表P［i］和P［j］，P［i］和P［j］两个完全相同（i＝1，2，…，N，P［i］为第i个边缘点，其x，y坐标分别记为P［i］.x，P［i］.y；j＝1，2，…，N，P［j］为第j个边缘点，其x，y坐标分别记为P［j］.x，P［j］.y）。

图2 轴式样的工业CT切片

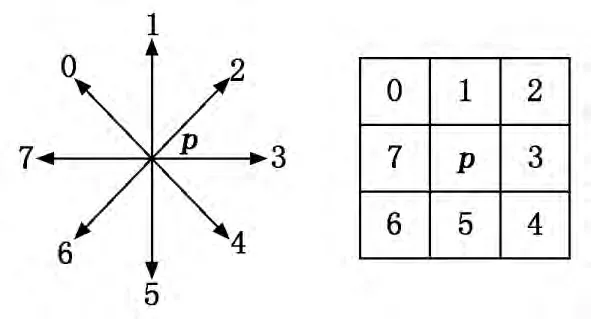
图3 方向链码示意图

表1 链码值与坐标值转换表

设数据链表P［i］中的某点为参考点，通过计算确定参考点与数据链表P［j］中点之间的距离D是否满足关系式（1），即：

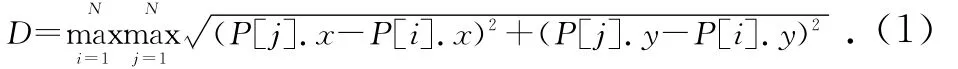
若D满足式（1），则直线的起始点和终止点坐标分别对应数据链表的P［i］和P［j］坐标，直线拟合裂纹时用直线连接起始点和终止点即可。

1.3.3 圆边缘拟合

本文对轴式样的外部轮廓进行圆边缘拟合，采用最小二乘法，不仅可以得到较高的拟合精度，而且相对计算简单。根据最小二乘法的基本内容，在 残余误差平方和最小情况下，可以得到最可信赖值［4］。首先，通过边缘跟踪切片上的圆形目标区域，得到一系列轮廓边界点，边界点个数记为N，第i个（i＝1，2，…，N）边缘点记为P［i］，其x，y坐标分别记为P［i］.x，P［i］.y。则圆方程可表示为：

其中：x0，y0为圆心坐标 ；r为圆半径。

对该轴圆形轮廓线采用非线性最小二乘法进行拟合，其优化目标函数为：

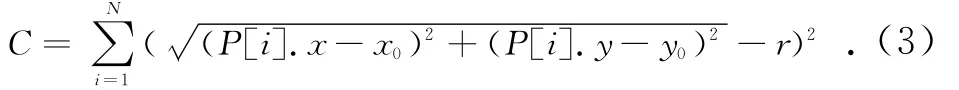
最小二乘法是优化目标函数达到最小值时，即可求出目标区域内的未知参数值。拟合时以圆半径作为限制条件，并根据拉格朗日乘数法，其最小二乘优化目标函数为：

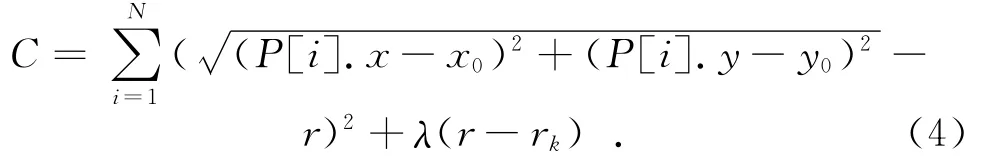
其中：λ为加权系数；rk为约束圆半径。

通过将约束最小二乘法转为无约束最小二乘法，利用高斯－牛顿或者 Levenberg-Marquardt法［5］可以求解相关参数。圆边缘拟合如图4 所示。

1.4 有限元分析

由于轴类材料一般为合金钢，属于脆性材料，长径比一般大于10，扭矩沿圆周方向分布，可以把轴类零件裂纹扩展当作平面应变问题，运用疲劳K理论（疲劳K理论主要用于材料变形后出现平面应变问题，也适用于大型零件和脆性材料的裂纹断裂分析）建立裂纹失稳扩展准则，对于只承担扭矩的轴类零件，零件内部近似只分布剪应力，因此裂纹可简化为滑开型裂纹模型，即裂纹扩展采用应力强度因子KⅡ准则。

常用的求解应力强度因子的方法有解析法和数值法，但解析法很难得到精确的边缘，因此运用有限元分析方法计算裂纹尖端的应力强度因子。有限元分析裂纹尖端应力强度因子的具体步骤如下：

（1）建立轴式样加载模型（只承受扭矩），如图5 所示。其弹性模量为2.1×105MPa，泊松比为0.3。

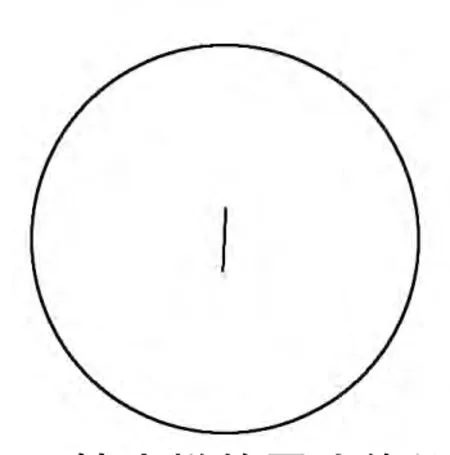
图4 轴式样的圆边缘拟合

图5 加载模型

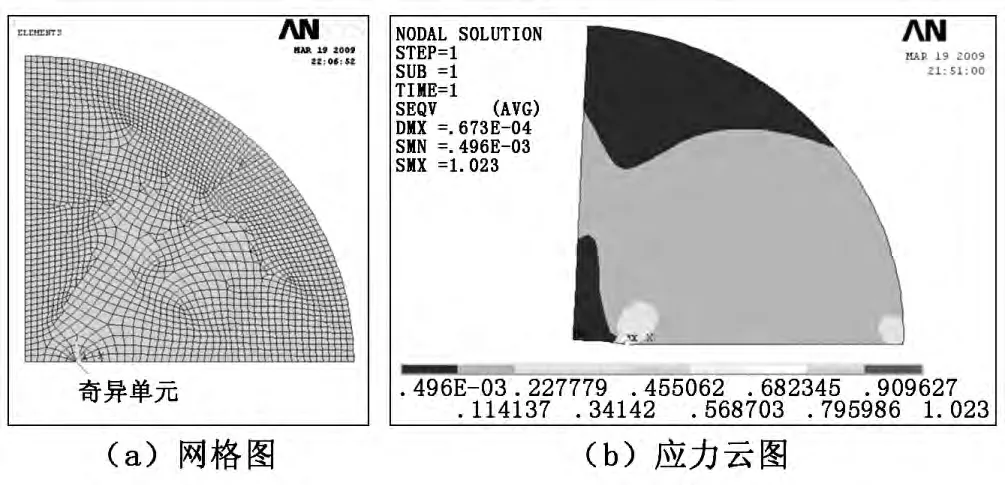
图6 轴式样的有限元网格和应力分布

2 结果与讨论

针对轴类零件内部裂纹难以测量及诊断的问题，本文提出了基于工业CT的轴类零件故障诊断方法。该方法可以获得深埋裂纹的在轴内部的位置及形状。根据重构出的只受纯扭矩的轴类零件裂纹扩展模型，利用有限元法及准则，可求出应力强度因子，作为判断轴类零件裂纹发展及性能评估依据，实现轴类零件的故障诊断。

［1］仵彦卿，曹广祝，王殿武.基于X－射线CT方法的岩石小裂纹扩展过程分析［J］.应用力学学报，2005，22（3）：484-490.

［2］John Canny.A computational approach to edge detection［J］.Pattern Analysis and Machine Intellgence，1986，8（6）：679-698.

［3］Wu Jong，Zhang Xiubin，Zhang Feng.The experiment research of edge detection in digital image ［J］.Microcomputer Information，2004，20（5）：106-107.

［4］费业泰，陈晓怀，秦岚，等.误差理论与数据处理［M］.北京：机械工业出版社，2004.

［5］Wei Zhen-zhong. Flexible on-line 3Dcoordinates measurement system based on machine vision ［D］.Beijing：Beijing University of Aeronautics and Astronautics，2003：10-15.