不含弦 6-圈的平面图的线性 2-荫度

常晶晶，徐常青

（ 河北工业大学 理学院，天津 300401）

不含弦 6-圈的平面图的线性 2-荫度

常晶晶，徐常青

（ 河北工业大学 理学院，天津 300401）

线性 2-森林是每个连通分支是长度至多为 2 的路的图，图 G 的线性 2-荫度是将 G 边分解为 k 个线性 2-森林 的最小 k 值 ，记为 la2G ．证 明了若 G 为不含弦 6-圈的平面图 ，则 la2GG/2+6 ．

平面图；荫度；线性 2-荫度；边分解

0 引言

图的线性 k- 荫度是由 Habib 和 Peroche[1]提出的．目前已经确定了某些特殊图：圈、树、完全图、完全二部图[2-4]的线性 2-荫度．文献 [5] 得到了平面图的线性 2-荫度的一般上界，并给出了不同围长的平面图的线性 2-荫度的上界．文献 [6] 改进了平面图线性 2-荫度的一般上界，得到．文献 [7] 证明了每个不含弦 5-圈的平面图的线性 2-荫度满足．本文证明了不含弦 6-圈的平面图的线性 2-荫度满足

下面给出一些基本记法．设图G为平面图，用F G 表示图G的面集合．任一表示面 f的度，即面 f边界的长度．度 d f=i的面称为 i面表示与顶点 v 关联的 i面数．任一表示顶点 v 的度，在不引起混淆时简记为 d v ．k- 点表示度为 k 的点，k+- 点表示度至少为 k 的点．称一个偶圈为 2-交替圈，若满足

定义1 任给平面图G，若G的任意一个非平凡分支H都有下列情况之一成立：

引理 1[8]设图 G 为平面图，若 G 为 k,1-遗传图 （9k14），则

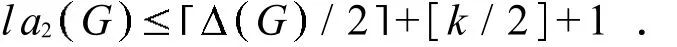
引理 2[9]设图 G 为 G3 且不含弦 6-圈的平面图，那么 G 中存在一条边 xy ，使得 d x+d y9．

1 主要结果

因为 G 不含弦 6-圈，故不存在 4 个依次相邻的 3 面，从而有断言 1：

要证断言 2成立，只需证与 v 关联的任意6个依次相邻的面中必有一个 5+面，用反证法证明此结论成立．设与 v 关联的 6 个依次相邻的面分别为 f1, ,f6，均为 3-面或 4-面．显然不存在 3 个依次相邻的 4面．由断言 1 可知，每 6 个依次相邻的面中至多有 3 个 3-面依次相邻．

1） 存在 3 个 3-面依次相邻．设 fi,fi+1,fi+2为 3 个相邻 3-面．

① i=1 （或者i+2=6)．不妨设 i=1 ，即 f1,f2,f3为 3 个相邻 3-面，f4为 4-面，此时当 f5为 3-面时，出现弦 6-圈．当 f5为 4-面时，出现弦 6-圈或者 2-交替圈，矛盾．

下面设没有 3 个依次相邻的 3-面．

2） 两个 3-面相邻．设 fi,fi+1为 2 个相邻 3-面．

① i=1 （或者i+1=6)．不妨设 f1,f2为两个相邻 3-面，f3为 4-面，若 f4为 4-面，出现弦 6-圈或者 2-交替圈，故 f4为 3-面．若 f5为 3-面，出现弦 6-圈，故 f5为 4-面．当 f6为 3-面时，出现弦 6-圈．当 f6为4-面时，出现弦 6-圈或者 2-交替圈，矛盾．

3）任两个 3-面不相邻．

① f1为 3-面，f2为 4-面．当 f3为 4-面时，f4为 3-面，则出现弦 6-圈或 2-交替圈，矛盾．当 f3为 3-面时，f4为 4-面，而 f5为 3-面或 4-面，出现弦 6-圈或 2-交替圈，矛盾．② f1为 4-面．

若 f2为 4-面，则 f3为 3-面．从而 f4为 4-面．若 f5为 3-面，则出现弦 6-圈，故 f5为 4-面．若f6为 3-面，则出现弦 6-圈；若 f6为 4-面，则出现弦 6-圈或 2-交替圈，矛盾．

若 f2为 3-面，则 f3为 4-面．若 f4为 4-面，则 f5为 3-面，出现弦 6-圈或 2-交替圈，矛盾．若f4为 3-面，则 f5为 4-面，出现弦 6-圈，矛盾．

综上可得断言2成立．

下面运用权转移方法证明结论．

给定如下权转移规则：

R1 每个 2-点从它的 2-主点得权 2．

R2 每个 3-面从与之相邻的每个 5 点或 6 点得权 1 ；从每个与之相邻的点得权

R3 每个 4-面从与之相邻的每个 6+点得权 1 ．

R4 每个 5-面从与之相邻的每个 6+点得权．

1） f v=5 ，由 G 不含弦 6-圈且无 2-交替圈，知，故由R2 得

3

34

3

4） f3v2 ，由及R2～ R4得

1） f3v=6 ，由断言 2 知，因 G 不含弦 6-圈且无 2-交替圈，故有，由R1～R3 得

2） f3v=5 ，由断言 2 有，若 f4v=2 ，则 f5v=0 ，由 R1～R4 得；若由 R1～R4得

34）， 断言 2 有，由及 R1～R4得5），由及R1～R4得

1） f3v=7 ，因 G 不含弦 6-圈且无 2-交替圈，故有，由R1 ，R2 得

2） f3v=6 ， 由 断 言 2 有， 且 由及 R 1～R 4 得

3） f3v=5 ， 由 断 言 2 有， 且 由及 R 1～R 4 得

3

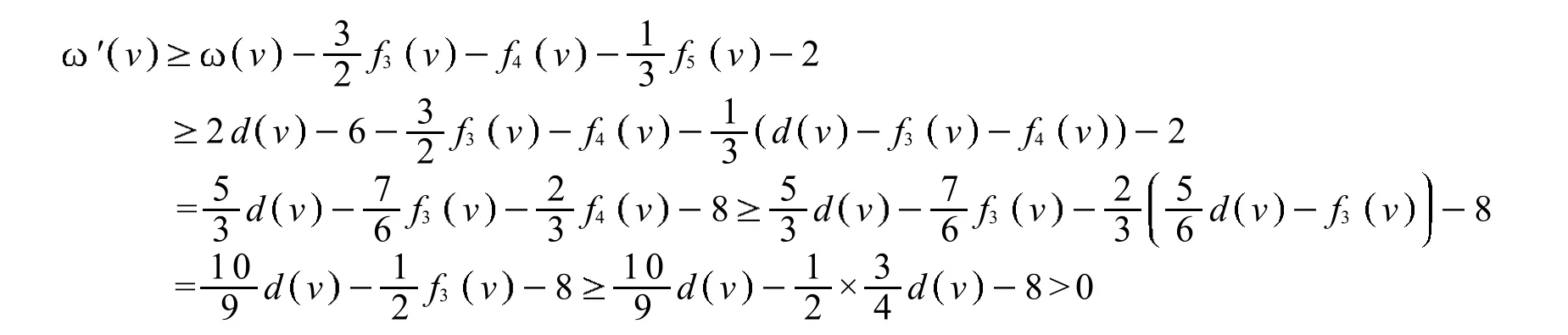
故结论成立．

由定理1知不含弦 6-圈的平面图为 10,1-遗传图，故由引理 1 即得如下结论：

定理 2 若 G 为不含弦 6-圈的平面图，则 la2GG/2+6 ．

[1]Habib M，Peroche B．Someproblemsabout lineararboricity[J]．DiscreteMath，1982，41（2）：219-220．

[2]Fu Hunglin，Huang Guoqing．The linear 2-arboricity of completebipartitegraphs[J]．ArsCombin，1994，38（3）：309-318．

[3]Chen Bailiang，Fu Henglin，Huang Guoqing．Decomposing graphs into forestsof pathswith size less than three[J]．Australas JCombin，1991，3（1）：155-73．

[4]Yen Chihhung，Fu Hunglin．Linear 2-arboricity of the completegraph[J]．Taiwanese JMath，2010，14（1）：273-286．

[5]Lih Kowei，Tong Lida，WangWeifan．The linear2-arboricity of planargraphs[J]．GraphsCombin，2003，19：241-248．

[6] 徐常青，安丽莎，杜亚涛．平面图线性 2-荫度的一个上界 [J]．山东大学学报：理学版，2014，49（4）：38-40．

[7] 田夏云．平面图的线性荫度和线性 2-荫度 [D]．济南：山东大学，2011：24．

[8]Xu Changqing，Chang Jingjing．The Linear2-Arboricity of Some Planar Graphs[J]．ArsCombin，2014，114：223-227．

[9] 钱景．图的线性荫度及线性 2-荫度 [D]．金华：浙江师范大学，2006：18．

[责任编辑 杨 屹]

The linear2-arboricity of planargraphsw ithoutchordal-6-cycles

CHANG Jing-jing，XU Chang-qing
(Schoolof Science,HebeiUniversity of Technology,Tianjin 300401,China)

A linear2-forestisa forestwhose componentsare pathsof length atmost2．The linear2-arboricity ofagraph G ，is the leastinteger k,so that G can be decomposed into k linear2-forests,which isdenoted by la2G ．Weget that if G isa planargraphw ithoutchordal-6-cycles,then la2GG/2+6.

planargraph;arboricity;linear2-arboricity;edge decomposition

1007-2373(2014)05-0076-04

O157.5

A

10.14081/j.cnki.hgdxb.2014.05.014

2013-09-29

国家自然科学基金青年基金（11301134）；河北省自然科学基金（A2011202071）

常晶晶（1987），女（汉族），硕士生．通讯作者：徐常青（1970），女（汉族），教授．