基于航班延误的机场调度调整优化研究
杨 欢,庞明宝,陈 静
(河北工业大学 土木工程学院,天津 300401)
基于航班延误的机场调度调整优化研究
杨 欢,庞明宝,陈 静
(河北工业大学 土木工程学院,天津 300401)
研究航班延误所引起的机场航班调整优化问题.在对航班延误所引起的多方决策主体分析的基础上,建立了包括乘客损失、机场运营成本增加、航空公司经济损失在内的加权和最小化的机场航班优化调整模型,采用遗传算法优化求解.具体机场的仿真实验表明该方法能快速实现航班调度动态更新,调整的方案能兼顾到乘客、机场和航空公司各方利益,使机场具有较好的综合服务水平,证明了该思想与方法的正确性与可行性.
智能运输系统;机场航班调度;航班延误;遗传算法;多主体决策
航班延误这一世界性问题已成我国各大机场的普遍现象[1-4].造成延误的原因有多种,但主要是在空中交通拥挤基本约束前提下由于天气原因、空域管制等不确定性因素所造成的[5-6],且这些对民用航空管理部门、机场等均为无法预知的突发事件.而一旦延误不仅对当前也会给后续(当天和很多天后)运行的航班、乘客等造成影响和损失,如何在已知航班延误信息的情况下尽快的调整后续机场航班计划以便使航班运营恢复正常且使影响和损失最小化成为空中管制部门、机场、航空公司和乘客所关心的问题[6-11].在理论研究方面,主要集中于从航空公司角度的航班延误后恢复问题,具体通过建立航空公司追求经济损失最小化相关模型,并予以优化处理得到新的调度方案[9-11],而在经济损失计算方面,部分研究仅考虑航空公司的损失,部分研究将可能对旅客的赔偿计算在内.显然这些是在具体航管部门、机场大调度实现优化前提下的具体航空公司调度优化,没有考虑到其它航空公司及其乘客的利益,不涉及机场可能增加的成本等,且航空公司对旅客的赔偿与乘客的损失不是一个完全等同的概念.而从机场、航管部门角度研究航班延误后机场调度较少,如胡明华以我国空域的基本情况和空中交通流量的相关特点为基础[5],提出多元受限的地面等待问题.这些为从机场、航管部门角度对可能造成的航班延误后调整优化调整提供基础,但这些研究都是针对某一类特定情况的,没有结合具体机场进出港航班表进行模型的建立及其相关优化计算,不能实现航班延误后快速的动态更新;在计算目标函数方面,仅考虑到航空公司和旅客损失两个方面,且同等看待,没有考虑到机场运营成本增加部分.实际上由于民用航空管理系统环境的不确定性以及动态实时性,在出现航班延误时,必须迅速的对后续航班进行动态调整才能满足实际的基本需要,而科学公平合理的优化调整才能满足包括航空公司、机场、旅客等多方利益主体的需要,才能最大限度的提高民航服务水平和取得社会效益最大化;而在目标函数值优化计算方面,不仅需要考虑到航空公司、旅客两方面损失,还需要考虑到机场可能增加的成本,且在不同条件下,三方权重可能有所差别,如旅客权重有所加大以体现公用基础行业特点.基于此,考虑到问题的复杂性,本文从机场、航管部门角度,尝试建立单一机场的包括乘客损失、机场运营成本增加、航空公司经济损失在内的加权和最小化的航班延误机场调度快速动态调整优化模型,通过算例来验证该思想方法的正确性.
1 机场调度动态调整模型
在航班延误情况下机场调度动态调整必须考虑到航空公司损失、旅客损失和机场成本增加3个方面,且以机场航班调度仿真模型为基础平台.模型中变量表示为:F为航班的集合,J为管制区集合,T为航班可行的起飞时间段集合;角标中 i为航班下标,j为管制区下标,t为时间下标,本模型中 1m in为一个离散化步长,k 为飞机下标.DTi为航班 i预计起飞时间,为最大延误时间为 t时刻管制区 j的容量,Ds t 为 t时刻机场的起飞容量,As t 为 t时刻机场的降落容量,vi为航班 i实际载客人数,pi为航班 i的票价,Et为等待在机场上空准备降落的飞机数,Vt为等待在机场起飞的飞机数,ti为航班 i的实际起飞时间,为相邻两架航班最小起降时间间隔.w1、w2、w3分别为航班动态调整时决策者对旅客,机场,航空公司的权重,即偏重程度,gk为飞机 k 单位时间的延误成本,S 为每位旅客单位时间的损失成本,ci为取消航班i的成本 (按照延误 8 h的延误成本计算取消成本),Hi为每位旅客单位时间的恢复成本 (包括赔偿费、安置费、转签费)等.

gk为条件变量,用于确定不同型号飞机的单位时间损失成本,本研究具体定义为

以一个机场为例,其优化模型表示为

模型中目标函数即式 (1) 表示追求加权总成本费用最小化,其中第 1 项、第 2 项为乘客费用,分别表示旅客失望溢出成本和旅客延误损失,第3项为机场负担的恢复成本,即机场增加的成本,第4项、第5项分别表示航空公司的延误成本和取消成本.
约束中式 (2) 表示航班 i实际起降时间不能早于计划起降时间;式 (3) 为航班延误时间不能超过飞机最长延误时间;式 (5) 是 t时刻等待起飞的飞机数量不能超过 t时刻机场跑道的起飞容量;式 (6) 是 t时刻等待降落的飞机数量不能超过 t时刻机场跑道的降落容量;式 (7) 是 t时刻起飞的飞机数量不能超过管制区的容量;式 (8) 为 0-1 变量约束.式 (4) 为对相邻两架飞机起(降) 时间间隔约束,按照民航具体规定标准为:前机为大型机时,后机为大型机、中型机、小型机的时间间隔最低标准分别为 1.5m in 、2m in 、2.5min ;前机为中型机时,后机为大型机、中型机、小型机的时间间隔最低标准分别为 1m in 、1m in 、1.5min ;前机为小型机时,时间间隔最低标准分别为 1m in .
式 (10) 表明本优化模型是建立在机场运营调度仿真模型基础上.
2 模型的优化求解
考虑到模型中决策变量为 0-1 变量,本研究采用浮点遗传算法进行优化求解,具体步骤为:
1)设定遗传算法的各参数:群体规模 MN 、最大迭代次数 NN 、交叉概率 JPc、变异概率 JPm、代沟 G等.定义适应度函数为

其中MMM为非常大的数.
2)随机产生 MN 组可行的航班调整方案,其中编码采用二进制,决策变量作为染色体,为 1值编码为1,否则为 0.同时设置迭代计数器.
3)在第 n代,计算每一个个体(即航班调整方案)的适应度.
4)若 n>=NN ,选择最优个体为最佳航班调整方案,输出.否则转向 5).
5) 选择最 优 Noverlap=MN × 1 G 个 个体直接 进入下一 代.同时 按照遗传 算法复 制、交叉 和变异规 则,产生下一代其余 MN Noverlap个个体,即新一组可行的航班数.
6)令 n=n+1 ,转向 3).
3 实验分析
为说明问题,本文以呼和浩特机场某一天航班调度为例进行分析.该机场正常航班时刻表见表1(仅列出部分航班).假定每位乘客单位时间的延误成本 S 为 2 元/min ,每位乘客单位时间的恢复成本 Hi为 2 元/min .
假设该天早晨 7:20 呼和浩特机场下雾,导致航班延误,预计在上午 9:00 恢复正常,可以正常起飞;上午 8:00 接到临时通知,10:20 的GS6485 航班飞机由于起飞时出现故障,晚点 30m in到达呼和浩特机场;该天 12:30 到 15:30 进行空中管制,不允许进行飞机的起降.对于延误航班,该机场尽可能在当天 24:00之前全部起飞,不取消航班,不影响明天航班的正常运行.
取 w1w2w3=1 1 1 ,按照 1、2 的方法确定后续航班新的时刻表,其中遗传算法求解时群体规模MN=40,代沟 G=0.9 ,交叉概率 JPc=0.7 ,变异概率 JPm=0.05 ,最大迭代次数 NN=600 .具体目标函数均值及其每代最优值变化见图1,可以看出迭代到第 100 代时,开始收敛,达到最优,这表明本方法快速更新后续航班的可行性.优化后的航班时刻表(方案 1)见表1,其中旅客损失、机场成本增加和航空公司损失分别为 3 509.23 、1 191.43 、5 716.95 万元,总目标函数值为 10 417.61 万元,显然在各种成本费用中航空公司损失最大,其次为旅客损失,而对机场等损失最小.

图1 600 代目标函数最优值、均值的变化Fig.1 Changesof thebestobjective function valueand the averageobjective function valuebefore the600th generation
为对优化方案进行比较,本研究按照现有航班延误后调度更新方案(方案2)进行调整,该方案为在不影响其他正常航班起降的情况下,对已有延误航班进行插空安排,调整后的航班时刻表略,其中一些航班找不到合适的插空位置,造成航班长时间延误,使得乘客大规模的滞留在机场.方案1和2具体造成的部分航班延误时间比较和成本比较见表2和表3.可以看出:采用本研究方法优化后方案的总延误时间小于根据经验插空安排的未优化方案的总延误时间,总成本费用 10 417.61 万元也小于依据经验方案的 10 657.52 万元.虽然依据经验调整的航班时刻表能保证正常航班的起降,但大大延长了延误航班上乘客的等待时间,造成大批乘客在机场滞留和航空公司航班的大调整,而本优化方案虽然会影响很多正常航班的起降时间,但在乘客损失、机场成本增加和航空公司损失以及合计方面均优于传统方案.且一些出现较短延误的航班,延误时间较短,大部分乘客可能在承受的范围内;对航空公司而言,小的延误可能在飞行途中赶回,即使不能赶回也对其可能的后续航班影响较小,这进一步证明了本研究方法的有效性.
为进一步说明优化更新机场航班延误时对各个主体利益的偏重,本研究对乘客、机场和航空公司利益取不同权重值时各项成本、总成本、加权总成本和归一化后的总成本进行实验比较,具体见表4.可以看出:三者的不同偏好,目标函数值会产生较大差异.由于当航班出现延误时,航空公司承担绝大部分的损失成本(包括乘客损失有可能由航空公司承担),其次是旅客和机场;而从整体航空调度而言社会效益最大化是优先目标,其次是航空公司的经济利益,而对机场等航空管理机构而言,由于其损失较小,而以其较小损失取得其它主体利益最大化是其应追求的,所以以优先偏重乘客利益,再偏重于航空公司利益,而最不偏重机场利益的方案为较佳选择.

表2 经验方案与优化方案造成的部分航班延误时间比较 m inTab.2 Comparison of delay time in partial flightsbetween normalupdating projectand optim ized project

表3 经验方案与优化方案各部分成本比较 万元Tab.3 Comparison of the partial costbetween normalupdating projectand optim ized project
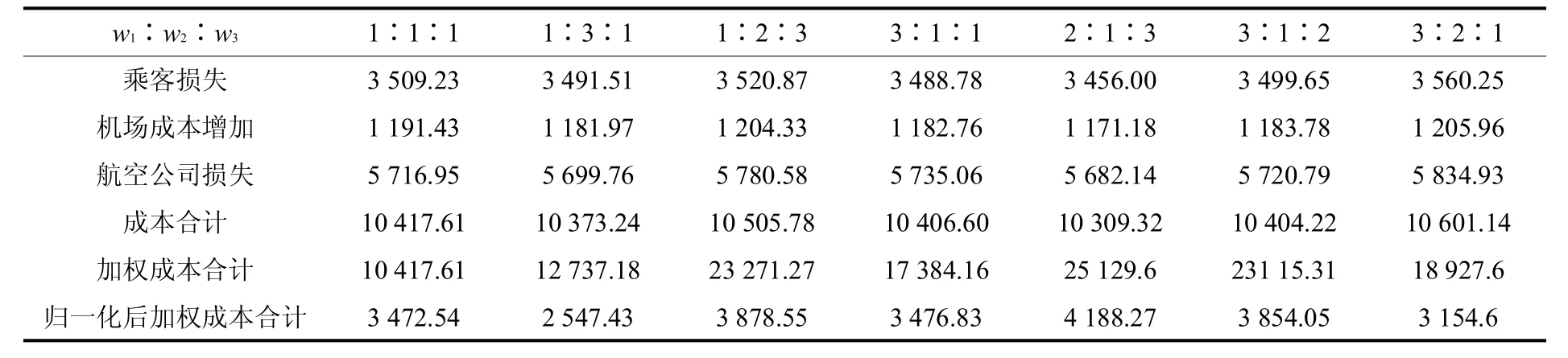
表4 不同偏好的优化方案各项成本比较 万元Tab.4 Costcomparison among optim ized projectsw ith the different favors
4 总结
在对航班延误所引起的多方决策主体分析的基础上,建立了包括乘客、机场和航空公司在内的加权和最小化的机场航班优化调整模型,具体机场的仿真实验证明了该思想与方法的正确性与可行性.该方法仅是机场航班延误优化调度的初始研究,仅限于单一机场,而进行多个机场航班延误后的动态调度优化研究,并将其推广到具体机场运营调度中将是下一步工作内容.
[1] 李雄,刘光才,颜明池,等.航班延误引发的航空公司及旅客经济损失 [J].系统工程,2007,25(12):20-23.
[2]Teodorovic D,StojkovicG.Modelto reducedairlinescheduledisturbances[J].Journalof Transportation Engineering,1995,121(4):324-331.
[3]Goran Stojkovic,FrancoisSoumis,JacquesDesrosiers.Anoptim izationmodel fora real-time flightscheduling problem[J].Transportation Research PartA,2002,36(9):779-788.
[4]Lan S,Clarke JP,BarnhartC.Planning for robustairlineoperations:optimizing aircraft routingsand flightdeparture times tom inim ize passenger disruptions[J].Transportation Science,2006,40(1):15-28.
[5] 胡明华.空中交通流量管理理论与方法 [M].北京:科学出版社,2010.
[6] 马辉,林晨.航班调度应急管理研究 [J].中国民航学院学报,2005,23(5):1-4.
[7] 白凤,朱金福,高强.基于列生成法的不正常航班调度 [J].系统工程理论与实践,2010,30(11): 2036-2045.
[8] 高强,严俊,陆宏兰.不正常航班旅客流恢复方法 [J].科学技术与工程,2011,11(27):1-4.
[9] 赵秀丽,朱金福,郭梅.不正常航班延误调度模型计算 [J].系统工程理论与实践,2008,28(4):2-4.
[10] 解天荣.基于延误成本的进港航班调度优化研究 [D].北京:北京交通大学,2008.
[11] 文优梅.基于遗传算法的航班进离港优化调度算法研究 [D].长沙:中南大学,2010.
[责任编辑 杨 屹]
Optim ization of updating forairportscheduling based on flightdelays
YANG Huan,PANGM ing-bao,CHEN Jing
(Schoolof CivilEngineering,HebeiUniversity of Technology,Tianjin 300401,China)
Theoptim ization ofupdating airportscheduling upon flightdelayswasstudied.Based on themulti-agentanalysis arising by flightdelays,amodelof optim ized updating scheduling for airport flightwas established tom inim ize the weightsum,which includes the lossofpassengers,the increasing operation costofairport,and the lossofairline corporations.Genetic algorithm wasadopted in theoptim ization course forsolution.Thesimulation resultof theconcreteairport indicates that the goalof dynamic updating rapidly flightscheduling is realized,the interestsof passengers,airport,and airline corporations are taken into account,and the airporthas a better synthetic service level by choosing themethod. And it thus proves the feasibility of themethod.
intelligent transportation system(ITS);airport flightscheduling;flightdelays;genetic algorithm(GA); multi-agentdecision
1007-2373(2014)05-0101-05
F562;V355
A
10.14081/j.cnki.hgdxb.2014.05.020
2013-11-09
河北省自然科学基金(E2011202073)
杨欢(1990-),女(汉族),硕士生.通讯作者:庞明宝(1966-),男(汉族),教授,博士.

