GPCA和遗传算法聚类分析在中国区域经济综合评价中的应用

周建新，付传秀

（1.皖西学院 应用文科实训中心； 2.皖西学院 金融与数学学院， 安徽 六安 237012）

GPCA和遗传算法聚类分析在中国区域经济综合评价中的应用

周建新1，付传秀2

（1.皖西学院 应用文科实训中心； 2.皖西学院 金融与数学学院， 安徽 六安 237012）

本文结合全局主成分分析（GPCA）和遗传算法聚类分析，对中国 31 个地区的经济发展水平进行综合评价.首先借助 GPCA 获得经济水平全局主成分分值，对区域经济发展进行纵向、横向分析；然后在GPCA 基础上，对区域经济发展水平做非线性映射的遗传算法聚类分析.仿真表明，综合评价结果与客观实际吻合度较高.

区域经济；全局主成分分析；非线性映射；遗传算法聚类分析

改革开放以来，中国经济迅猛发展，综合国力明显提高.同时，区域经济间的发展差距问题随之显现.按照科学发展观的要求，统筹区域经济协调发展成为现代化建设中的一个重大战略问题.正确评价中国各地区的经济发展水平，可以为区域经济均衡发展提供理论指导.

区域经济的发展是一个动态过程，对其评价应考虑时间因素.全局主成分分析（GPCA）在传统主成分分析方法的基础上，融入了时间序列的思想，适合从纵向、横向两方面评价中国各地区的经济发展水平.非线性映射的遗传算法聚类分析，是通过智能计算将众多的评价指标数据映射到二维空间，进行聚类分析，聚类结果的显示更为直观.

本文利用 GPCA和遗传算法聚类分析，对中国31个地区连续两年的经济发展水平进行综合评价，得到一些有意义的结论，可以为区域经济、社会的统筹发展提供决策参考.

1 中国地区经济发展的 GPCA

1.1 区域经济综合评价指标体系

区域经济的发展受政治、经济、文化、社会诸多因素影响，是一个复杂系统.对其客观评价，需要合理构建评价指标体系.

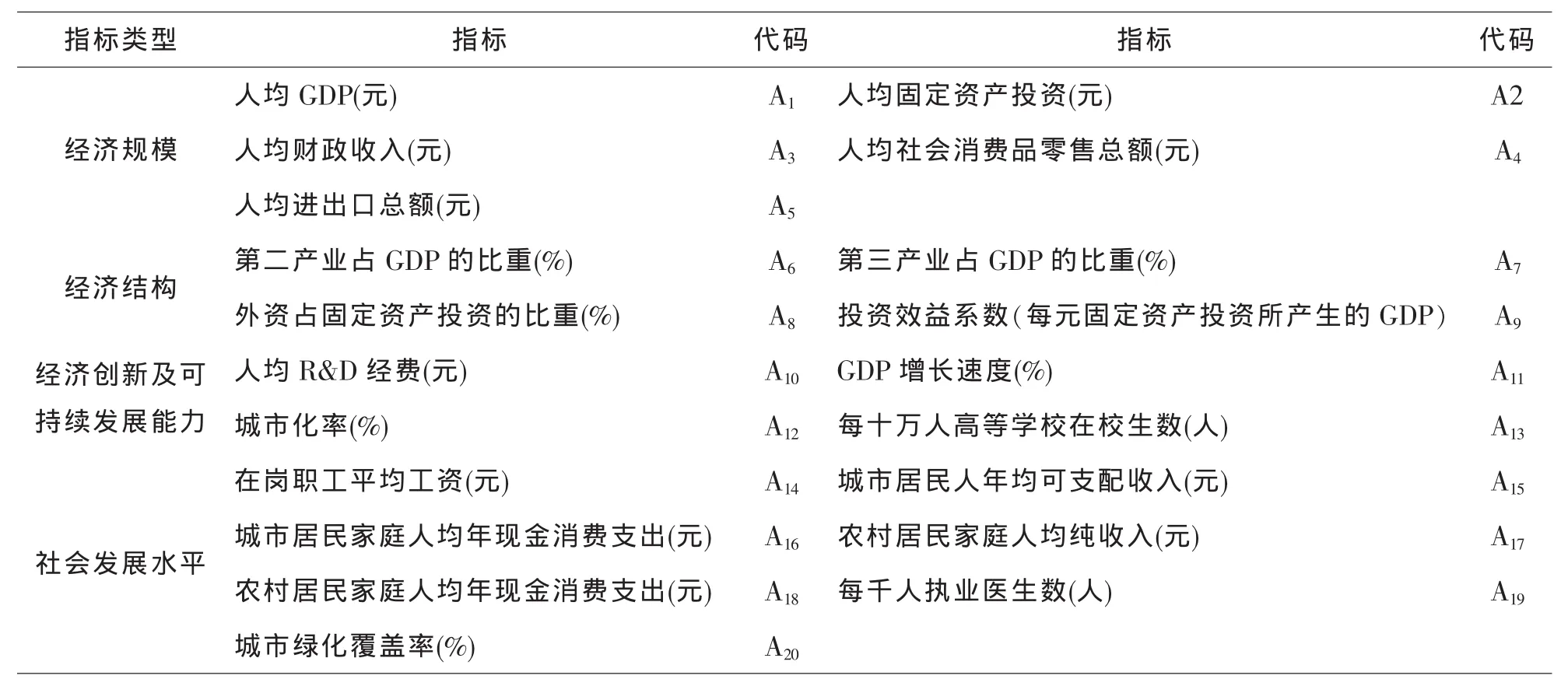
表1 区域经济发展水平评价指标体系

本文从经济规模、经济结构、经济创新及可持续发展能力、社会发展水平等方面综合衡量，选取反映区域经济发展水平的 20项评价指标，建立指标体系如表1：

1.2 全局主成分分析（GPCA）

经典主成分分析，是在样本评价指标组成的数据表基础上进行分析，无法实现不同时点样本的评价对比.全局主成分分析，是融入了时间序列思想的主成分分析方法，它首先将不同时点的若干数据表按时间顺序整合，得到一个全局数据表，然后进行经典主成分分析.

区域经济的发展一般以年为时间跨度加以评价分析，评价指标间具有数据相关性.通过 GPCA进行降维处理，保证了区域经济系统分析的整体性、统一性和可比性.

根据区域经济发展水平的评价指标 A1，A2，…，A20，选取中国 31个地区连续 2年的数据，整合为全局数据表，利用 Matlab7.0软件的 princomp函数进行全局主成分分析.

2 非线性映射的遗传算法聚类分析

2.1 非线性映射

非线性映射分析是 Sammon于 1969年提出的一种几何降维数学方法，是通过非线性变换，用少数几个综合变量最大限度地表达高维变量,将高维空间问题转化为直观的低维空间问题.

非线性映射由高维变换到低维的约束条件，即误差函数为：分别为高维空间和低维空间中样本点 i、j之间的欧氏距离.

2.2 基于遗传算法工具箱的聚类分析

遗传算法是借鉴生物界中自然选择原理、自然遗传机制的一种全局寻优算法，其实质是通过群体搜索技术，根据适者生存的原则逐代进化，最终得到最优解或准最优解.其构成要素：染色体编码，个体适应度评价，遗传算子（选择、交叉、变异），运行参数设置.

Matlab7.0软件的遗传算法与直接搜索(Genetic Algorithm and Direct Search)工具箱可以优化目标函数.利用遗传算法工具箱对非线性映射的误差函数做最小化处理，找到合适的二维数据结构，完成高维数据到二维数据的非线性映射，实现样本的聚类分析.

3 实例分析与结论

3.1 选取中国 31个地区连续 2年的数据，进行GPCA

根据区域经济发展水平评价指标体系，选取中国 31个地区在 2010年和 2011年的 31×2×20个数据，整合为全局数据表.经 GPCA可知，前 4个主成分的累积贡献率达到 85%，故选择 4个主成分作为综合指标，代替原有的 20个指标.2010、2011年地区经济发展水平综合得分及排序如表2：

表 2 2010、2011年地区经济发展水平综合得分及排序

经验证，GPCA综合得分及排序与中国各地区经济发展水平基本相符，表明区域经济水平的评价指标体系构建合理.

由表 2纵向、横向比较可知，中国经济在 2010年和 2011年发展平稳，东部、东北、中部、西部各区域经济发展均衡.经济发展的整体格局稳健，其中，东部发展较迅速，中部尤其是安徽崛起显著.

3.2 利用遗传算法工具箱，进行 2011年中国各地区经济发展水平的聚类分析

将 2011年的主成分分值作为样本数据，在Matlab7.0中调用遗传算法工具箱，完成高维数据到二维数据的非线性映射，实现样本的聚类分析.

选取一次的仿真结果并分析如下：

当遗传算法停止，种群进化完毕，得到如图 1所示的最优个体适应度函数值变化曲线及最优个体.最优个体对应的适应度函数值为 0.0137878，比较接近 0，说明遗传算法较好地找到了非线性映射时误差函数的解.

根据最优个体的值，得到高维数据映射到二维空间的结果如图 2（标号对应的地区见表 2），从图中可看出各样本的聚类情况.2011年我国 31个地区的经济发展水平大致可分为 4类，分别为：A类（经济发达地区）：北京、上海；B类（经济较发达地区）：天津、浙江、广东、江苏、福建、辽宁、山东、内蒙古；C类（经济中等发达地区）：重庆、海南、吉林、湖北、河北、陕西、黑龙江、山西、湖南、宁夏、江西、安徽、四川、河南、新疆、广西；D类（经济欠发达地区）：青海、云南、西藏、甘肃、贵州.其中，北京、上海的经济发展水平明显高于其它地区；广东、浙江、江苏、天津的经济发展水平也较高.

由 GPCA和遗传算法聚类分析的结果，可以得出以下结论：

(1)将 GPCA和非线性映射的遗传算法聚类分析相结合，可以为区域经济评价提供了一种新的思路和方法.GPCA可根据综合分值对区域经济发展水平进行纵向、横向比较；非线性映射的遗传算法聚类分析，实现了在二维平面中直观地看到高维样本点的近似图像，避免了其它聚类法的人为选择因素.

(2)GPCA得分值与遗传算法聚类分析的结果基本吻合，实现了定量与定性的统一，结果较为理想.从 GPCA的结果来看，中国各地区经济在 2010年和 2011年期间整体发展平稳；从遗传算法聚类分析的结果来看，中国各地区经济发展的差距较大，特别是东西部间差距明显，统筹区域经济协调发展的任务十分紧迫.

本文结合 GPCA和遗传算法聚类分析，对中国地区发展水平进行综合评价.首先借助 GPCA获得经济水平全局主成分分值，对区域经济发展进行纵向、横向分析；然后在 GPCA的基础上，对区域经济发展水平做非线性映射的遗传算法聚类分析.仿真显示，综合评价结果与客观实际吻合度较高，表明GPCA和遗传算法聚类分析相结合的综合评价方法，在中国区域经济评价中的应用是合理有效的.

图1 遗传算法中最优个体适应度函数值变化曲线及最优个体

图 2 2011年中国区域经济发展水平二维空间映射结果

〔1〕高洪深.区域经济学(第三版)[M].北京：中国人民大学出版社,2010.7-21.

〔2〕何晓群.多元统计分析(第三版)[M].北京：中国人民大学出版社,2012.114-128.

〔3〕张建平.基于主成分分析的区域经济发展水平的综合评价[J].农业与技术,2007（6）：125-128.

〔4〕耿海清,陈帆,詹存卫等.基于全局主成分分析的我国省级行政区城市化水平综合评价[J].人文地理,2009（5）：47-51.

〔5〕陆仁强,张宏伟,牛志广等.基于非线性映射理论的城市供水管网压力监测点布置方法研究[J].水利学报,2010（1）：25-29.

〔6〕雷英杰,张善文,李续武等.MATLAB 遗传 算法工具箱及应用[M].西安：西安电子科技大学出版社,2006.

〔7〕韩瑞锋.遗传算法原理与应用实例[M].北京：兵器工业出版社,2009.25-36.

F224；O29

A

1673-260X（2014）08-0107-03

基金支持：六安市定向委托皖西学院市级研究项目（2012LW 020）；安徽高校省级科学研究项目（KJ2013B332）