MEMS惯组抗高g值冲击设计方法

汪守利，刘海涛，滕 纲，刘尔静，张 钰

（北京遥测技术研究所，北京 100076）

MEMS惯组抗高g值冲击设计方法

汪守利，刘海涛，滕 纲，刘尔静，张 钰

（北京遥测技术研究所，北京 100076）

MEMS惯组以其体积小、成本低、可靠性高在强冲击环境中得到越来越广泛的应用。为解决基于石英微陀螺和硅微加速度计的MEMS惯组抗高g值冲击问题，提出了一种内减振抗冲击设计方法。在该设计方法中，将陀螺与加速度计嵌入式安装在对称六面体框架结构上，并通过粘接在六面体框架八个顶点的 24块粘弹性阻尼减震器与惯组基体隔离，实现内减振。同时基于弹簧阻尼系统理论建立了MEMS惯组抗冲击等效数学模型，对模型进行了仿真分析。利用有限元分析软件ANSYS对三维结构模型进行了模态分析和冲击仿真分析，并通过结构扫频实验与9次5000g冲击谱试验进行了验证。仿真分析与试验结果证明了该方法的有效性及可行性。

石英陀螺；MEMS惯组；弹簧阻尼系统；高g值；冲击

基于石英微陀螺与硅微加速度计的 MEMS惯性测量单元（简称“MEMS惯组”）以其体积小、重量轻、成本低、耐冲击等特性，广泛应用于导弹、火箭弹、炮射武器等的遥测系统及控制系统，用于测量载体的角速度及加速度，实现弹体的姿态稳定和制导飞行。在弹体发射及飞行过程中，存在着爆炸分离等强冲击过程。爆炸冲击多由火工装置动作产生，其冲击量值较大，可达 103～105g[1]，频带较宽，从几百赫兹至上万赫兹，极易导致弹上产品工作失效甚至损坏。为保证MEMS惯组在强冲击过后能够正常工作，需要对其进行抗高g值冲击设计。

1 结构设计与仿真分析

由国产石英音叉微机械陀螺和硅微机械加速度计组成的MEMS惯组已经获得了多个型号成功应用，能够适应高冲击、强振动和大过载的恶劣环境。下面以应用于某型号的MEMS惯组为例，介绍其抗冲击设计方法。分离过程中产生的爆炸冲击量值较大，其冲击谱条件为50 Hz/100g—600 Hz/5000g—5000 Hz/5000g，如图1所示。

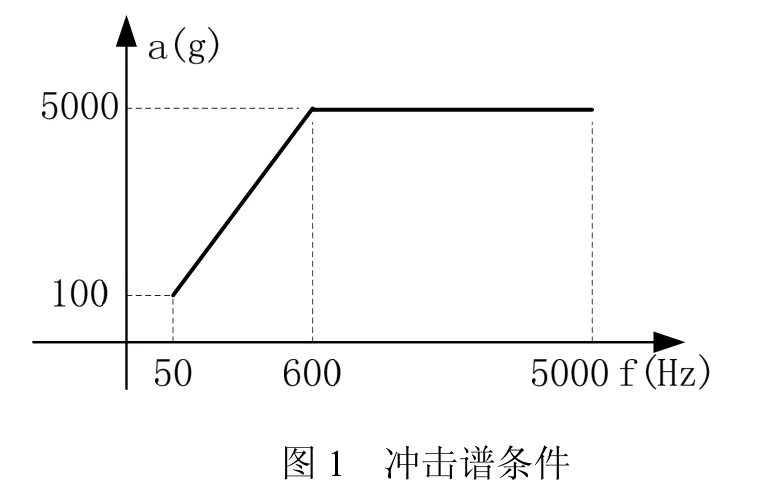
Fig.1 Shock response spectrum

1.1 结构设计方案

MEMS惯组由三支石英微陀螺仪、三支硅微加速度计、信号处理电路及结构体等组成。在惯组的抗冲击设计过程中，除了对电子元器件、印制板等的抗冲击设计考虑之外，重点需要考虑微陀螺仪及微加速度计的抗冲击减振设计。抗冲击性能一般用系统最大加速度和最大位移来评价[2]。从能量观点来看，抗冲设计实质上是把瞬时强烈的冲击能量，以位能的形式最大限度地储存在冲击减振器中，使减振器产生较大的形变。冲击结束后，减振器能缓慢地将能量释放出来，达到保护目的。减振模式的选取不仅影响着产品减振性能，也影响着产品的测量精度，历来是惯性产品结构设计的重要环节。理论上，可以采用的减振模式是多种多样的。但在工程应用中，由于弹体结构、弹体可提供的安装位置、惯性产品自身的结构特点等几何条件的限制，实际可采用的减振模式是非常有限的。目前，在捷联惯性产品的结构设计中最常采用的减振模式主要有六种[3-4]，且主要是针对惯性产品整机进行的减振设计。

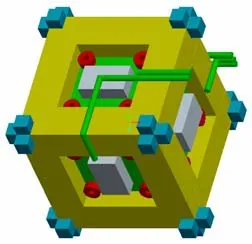
图2 IMU框架结构设计方案Fig.2 Design scheme of IMU frame structure

图2所示为MEMS惯组内部的IMU框架结构设计三维示意图。根据敏感元件及其安装印制板的结构尺寸，将 IMU框架设计为对称六面体结构，六个敏感元件分别嵌入正方体六个面。IMU框架采取八点减振模式，是文献[3]中长方体八点减振模式的特殊形式。对于抗冲击减振材料，选用粘弹性阻尼材料做减振垫，在冲击过程后，可以将部分能量以热能形式消耗在周围环境中。将带有减振垫的 IMU框架结构放入IMU基体内，并保证减振垫与IMU基体间存在一定的预紧力。通过对 MEMS惯组内部结构进行减振设计，避免了整机外减振带来的实际测量安装误差，也方便了产品的安装。对称八点减振模式共需要二十四块阻尼减振垫，其结构六自由度（三轴线运动、三轴角运动）上的运动互不耦合，彼此独立[5]，避免了给系统引入伪运动信号，从而影响测量精度。如果将 IMU基体看作刚体，可以按照单自由度系统情形进行等效模型分析。

1.2 等效数学模型分析

将 IMU框架看作一个质量块 m，则可以用图3所示的单自由度弹簧阻尼系统对 IMU框架结构进行等效数学模型分析。

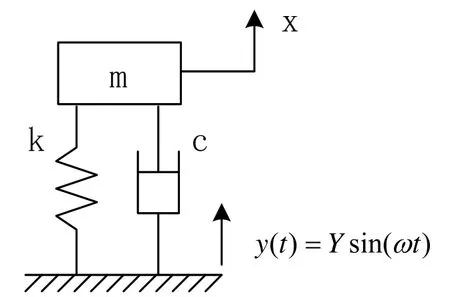
图3 单自由度弹簧阻尼系统Fig.3 SDOF spring-damper system

其中，k为等效刚度，m为等效质量，c为等效粘性阻尼系数。

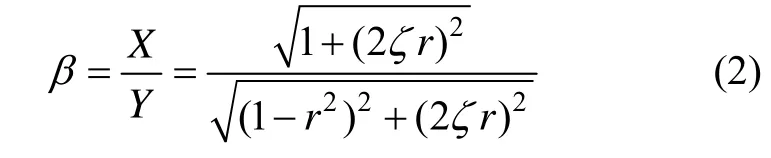
对于0＜ζ＜1，当频率比取[6]

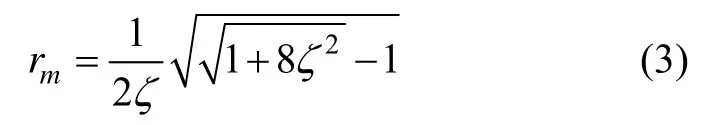
时，振幅放大系数β为最大值：

根据上述公式(4)，可得阻尼比：

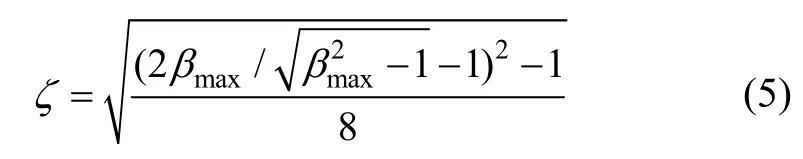
由于质量块加速度响应与位移响应成正比关系，质量块最大稳态加速度与基体最大稳态加速度的比也用式(2)表示。根据扫频试验结果，将扫频加速度响应峰值振幅放大系数代入式(5)，可以计算得到阻尼比ζ，再由式(3)可计算等效模型系统固有频率。

由公式(2)可以分析振幅放大系数与阻尼比及频率比的关系。如图4所示，当频率比小于时，振幅放大系数小于1，且随着阻尼比的增大，振幅放大系数变小，峰值频率比变小；当频率比大于时，振幅放大系数小于1。

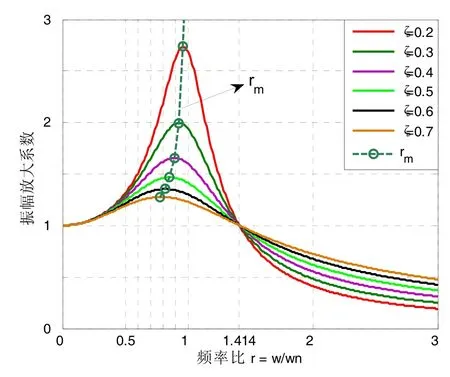
图4 模型参数关系Fig.4 Parameter relations of SDOF system model

由公式(2)，对于图1所示的冲击响应谱条件，可以分析等效模型在不同阻尼比及固有频率下的输出。图5所示为系统固有频率等于200 Hz时不同阻尼比情况下等效模型系统输出，图6所示为阻尼比等于 0.4时不同固有频率下等效模型系统输出。

在进行抗冲击设计的时候，还需要考虑产品的振动条件。航天用惯组产品振动条件多为宽带随机振动。随机振动环境试验的试验时间一般以分为单位，不同于冲击试验是在极短时间内完成，产品在其固有频率点附近将较长时间承受大于输入加速度的激励，这就要求系统的阻尼不能太小。如图5所示，阻尼比过低，在低频放大区，输出响应的放大倍数较大；阻尼比过高，在高频区，输出的衰减能力变弱。由冲击谱条件，在600 Hz拐点频率处的冲击谱值达到5000g。因此减振系统的谐振频率设计必须低于600 Hz，频率越低，传递到IMU框架的冲击量值将越小，如图6所示。考虑强冲击环境下的压缩变形，谐振频率过低将会导致阻尼减振垫的位移变形量过大，且系统要求加速度计的带宽为100 Hz，谐振频率过低会影响加速度计的测量精度。另外MEMS惯组选用的微敏感元件本身也具备一定的抗冲击能力。根据以上分析，减振系统的设计需要综合考虑系统测量精度、振动环境及所选敏感元件本身所能承受的冲击量值。

图5 不同阻尼比系统输出（fn=200Hz）Fig.5 Response of different zeta（fn=200Hz）

图6 不同固有频率系统输出（ζ=0.4）Fig.6 Response of different inherence frequency（ζ=0.4）

在IMU框架结构尺寸确定情况下，减振系统的设计，主要是减振材料的选取及其形状的设计。通过选取不同的减振垫片，对系统进行有限元仿真分析，来满足系统的设计需求。

1.3 有限元仿真分析

选取减振垫后，在ANSYS软件中输入相关材料参数进行有限元仿真分析。

图7 模态分析结果Fig.7 Result of mode analysis

图7为模态仿真分析，其一阶响应模态为241Hz。冲击仿真分析以应力集中最大的Y向进行说明。

图8所示为MEMS惯组Y轴按给定的冲击响应谱进行冲击仿真分析后的应力分布云图（IMU上盖板隐藏），图9所示为形变分布云图（IMU基体隐藏）。

通过图8可知冲击谱响应仿真分析最大应力为9.4803MPa，最大应力出现在IMU基体上，最大应力远小于IMU结构材料的许用应力180MPa。通过图9可知冲击响应谱仿真分析的最大变形为0.75694mm，最大变形出现在IMU减振垫上，变形量小于粘弹性阻尼减振垫的许用变形量。综上，仿真结果表明所设计MEMS惯组满足冲击试验条件的要求。

在系统的模态分析及冲击仿真分析阶段，可以设计不同的减振垫进行分析，以达到所需设计要求。通过有限元仿真分析，可以减少大量的摸索试验，从而节约成本和研制时间。由于有限元模态分析中需要进行刚性化或简化处理，仿真结果一般比实际结果略大。

图8 Y轴应力分布云图Fig.8 Stress distributing of Y-axis

图9 Y轴形变分布云图Fig.9 Deformation distributing of Y-axis

2 试验验证

2.1 扫频试验

为了验证等效模型及仿真分析的科学性，对MEMS惯组进行扫频试验。将惯组刚性安装于振动台上进行正弦频率扫描试验，结果如图10所示，当频率f=207.3 Hz时IMU框架结构处于谐振状态，峰值振幅放大系数为1.3183。谐振频率与仿真分析结果基本一致。根据公式(3)，计算系统的固有频率为256 Hz；根据公式(5)，计算系统的阻尼比为 0.6405。由 MEMS惯组的等效模型及输入冲击响应谱条件，可以计算IMU框架的全频点冲击响应。

图10 结构频率响应Fig.10 Frequency response of IMU structure

2.2 冲击试验验证

为实际验证上述抗冲击设计方法的正确性，对MEMS惯组按给定的冲击谱条件进行了冲击试验，通过检测敏感元件的输出信号，验证其抗冲击性能。试验中分别沿X、Y、Z轴三方向进行冲击试验，每方向试验三次。下面以Y向冲击试验为例进行说明。如图11所示为Y向冲击试验照片。

如图12所示为Y向冲击试验陀螺响应图，可以看出陀螺输出信号在冲击前后并无明显变化，陀螺性能良好。由图13可知，冲击前后加表输出无明显变化，加表性能良好。特别是，在冲击后，石英微机械陀螺和硅微机械加速度计数据在2 s时间内能够稳定。由此可知按照上述方法所研制的MEMS惯组三方向均能满足给定冲击谱试验条件的要求，且冲击后产品性能良好，输出零位无变化，未见输出信号异常。

图11 IMU Y向冲击试验Fig.11 Y-axis shock experiment of IMU

图12 Y向冲击试验陀螺响应Fig.12 Gyro response of Y-axis shock

图13 Y向冲击试验加速度计响应Fig.13 Accelerometer response of Y-axis shock

3 结 论

MEMS惯组以其体积小、成本低、可靠性高在强冲击环境中得到越来越广泛的应用。本文介绍了一种MEMS惯组抗高g值冲击设计方法，设计了对称六面体八点减振模式的结构方案，建立了MEMS惯组抗冲击等效数学模型，并利用有限元分析软件ANSYS进行了结构模态分析和冲击仿真分析，通过相关试验进行了验证。该方法在多个型号MEMS惯组的研制中得到应用，也可以作为其它产品抗冲击设计的参考。对于量级更大的冲击，则可以考虑对印制板、敏感元件等采取多级减振措施，来保证系统的抗冲击性能。

（References）：

[1]Brown T G，Davis B，Hepner D，et al.Strapdown microelectromechanical(MEMS) sensors for high-g munition applications[J].IEEE Transactions on Magnetics，2001，37(1):336-342.

[2]夏宇宏，姜洪源，魏浩东，等.金属橡胶隔振器抗冲击性能研究[J].振动与冲击，2009，28(1)：72-74.XIA Yu-hong，JIANG Hong-yuan，WEI Hao-dong，et al.Shock protection characteristics of metal rubber isolators[J].Journal of Vibration and Shock，2009，28(1):72-74.

[3]姚建军.捷联惯导系统不同隔振模式的比较[J].强度与环境，2009，36(2)：19-27.YAO Jian-jun.Contrast of different vibration isolation patterns used in strap-down inertial navigation system[J].Structure &Environment Engineering，2009，36(2):19-27.

[4]TUO Zhou-hui，HU De-wen，LI Ru-hua，et al.Damping design of strap-down inertial navigation system[J].Journal of Chinese Inertial Technology，2009，17(6):648-650.

[5]张志鑫，张大伟.捷联惯组减振系统角振动、线振动共振频率理论分析[J].中国惯性技术学报，2009，17(6)：654-657.ZHANG Zhi-xin，ZHANG Da-wei.Theory analysis on resonance frequencies of linear vibration and torsional vibration of strapdown IMU damping system[J].Journal of Chinese Inertial Technology，2009，17(6):654-657.

[6]Rao S S.Mechanical vibrations[M].5th Ed.London:Pearson Prentice Hall，2010:281-284.

Design method of MEMS IMU in high-g shock

WANG Shou-li，LIU Hai-tao，TENG Gang，LIU Er-jing，ZHANG Yu(Beijing Research Institute of Telemetry，Beijing 100076，China)

MEMS IMU is used widely in high-g shock environment for its small volume，low cost and high reliability.MEMS IMU based on quartz gyro and silicon accelerometer need to be protected in high-g shock environment.To solve the anti-shock problem，an inner damping method is introduced.Gyros and accelerometers are embedded in the symmetrical hexahedron frame.The frame is isolated from IMU base by 24 viscoelastic damping materials felted on the frame culmination.Anti-shock math model is built and simulated based on spring-damper system theory.Mode analysis and shock spectrum response analysis of 3-D structure are simulated based on ANSYS finite element.Structure frequency experiment and nine 5000gSRS experiments are implemented.The result of simulation and experiment validate the effectiveness and feasibility of this method.

quartz gyro;MEMS IMU;spring-damper system;high-g;shock;

U666.1

A

1005-6734(2014)03-0404-05

10.13695/j.cnki.12-1222/o3.2014.03.024

2013-12-23；

2014-04-16

总装十二五预研项目（51309010401）

汪守利（1981—），男，高级工程师，从事石英微惯性产品应用研究。E-mail：wangshouli414@163.com