多目标模糊决策算法研究

陈蓉素

宁波工程学院网络信息中心，浙江宁波 315211

多目标模糊决策算法研究

陈蓉素

宁波工程学院网络信息中心，浙江宁波 315211

1 引言

自从Zadeh在1965年提出模糊集理论[1]以来，模糊集理论得到了不断的发展和完善，并在许多领域中得到广泛的应用。作为模糊集的推广，Gau和Buehrer在1993年提出了Vague集[2]的概念，在这一理论中，Vague集通过真隶属度、假隶属度、核、未知度四个指标全面刻画[3]，Vague集对不确定模糊信息刻画得更加精确，处理更灵活。目前，Vague集在信息融合、模式识别、模糊决策等方面都有广泛的应用，并引起了国内外学者的高度重视[2-15]。接近理想点法是一种常用的多属性决策方法，它主要借助决策问题的“理想解”和“负理想解”排序选优，并已广泛应用于各种决策领域中[7-12]。但在实际应用中也发现它存在一些问题。例如，在实际生活中，决策者必须考虑多元化越来越强的决策环境，以期达到一个相对满意的目标水平。在文献[13]中，作者采用加权相对偏差距离最小原则，即取m个评价方案中与最理想方案之间的加权相对偏差距离最小者对应的方案为最优方案。本文采用一种新的算法，即对方案作两两比较，由于该方案的优劣关系不满足传递性，需引入拉格朗日乘数法解决一致性问题，并最终找到最优方案。

2 多目标模糊决策算法概述

多目标模糊决策问题就是要解决从一系列候选方案x1，x2，…，xm中如何选择一个方案，使得最满足要求。一般情况下，每个方案xi(i=1，2，…，m)有n个可应用的资源（或受到的约束条件）xi1，xi2，…，xin，由此建立决策矩阵X=(xij)mn。同时，设权重向量ϖ= (ϖ1，ϖ2，…，ϖn)T，其中，权重向量ϖ的第j个分量ϖj代表方案所受约束条件的第j个分量的权系数。依据对决策方案的描述，首先构建模糊决策矩阵并确定理想解和负理想解，后利用度量定义方案的相对贴近度并构建判别矩阵，最后引入拉格朗日乘数法解决一致性问题，并最终找到最优方案。

2.1 建立模糊决策矩阵

对于决策矩阵，首先运用9刻度法将定性指标量化得到数字决策矩阵A=(aij)mn，再运用最大隶属度方法得到模糊决策矩阵B=(bij)mn。候选方案所受到的约束条件一般有效益型和成本型两种，其中，效益型指标越大对于达成目标产生的作用越大，即越大越好，而成本型指标越小对于达成目标阻碍越少，即越小越好。因此可采用如下方法，对效益型指标选取其隶属度为：而对成本型指标选取其隶属度为：

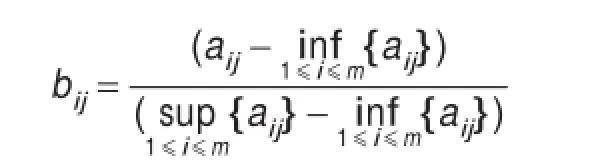
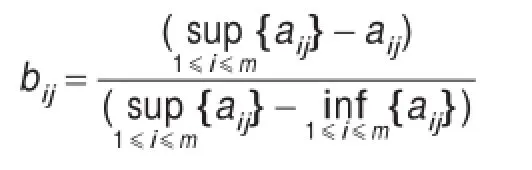
由此得到模糊决策矩阵B=(bij)mn，第i个方案xi对应的隶属度向量为bi=(bi1，bi2，…，bin)。

2.2 确定理想解xi∨xj和负理想解xi∧xj

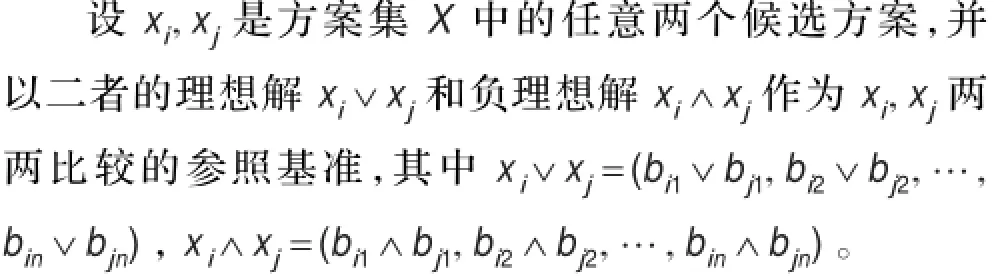
2.3 计算方案xi，xj的相对贴近度

首先计算方案xi，xj与理想解xi∨xj和负理想解xi∧xj的欧氏距离：

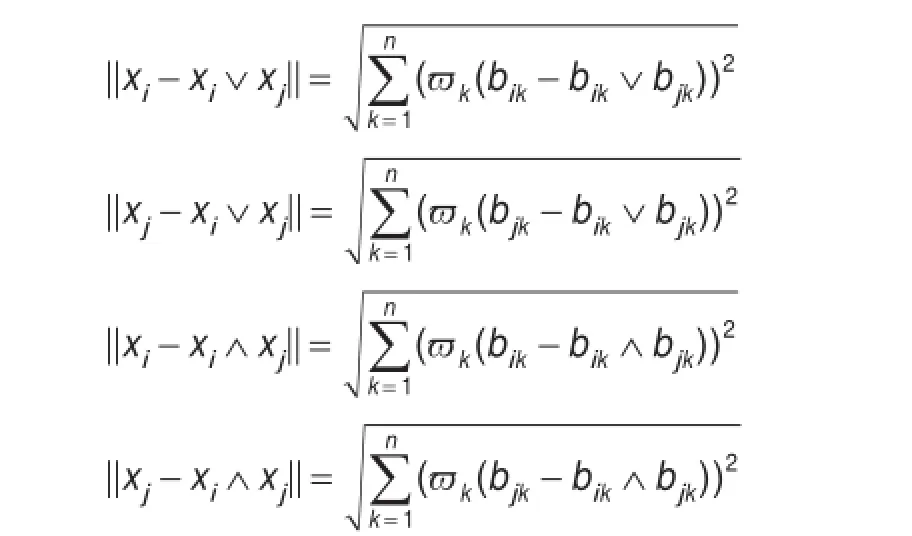
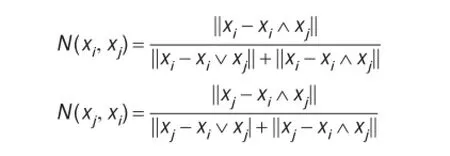
其次应用模糊模式识别中的贴近度概念，计算方案xi，xj的相对贴近度：

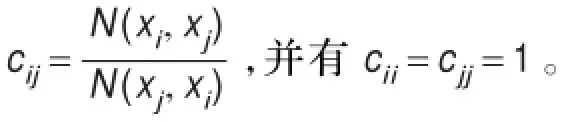
2.4 运用拉格朗日乘数法解决一致性问题

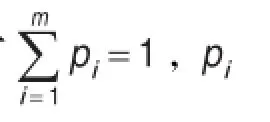
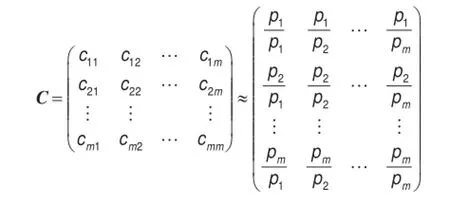
因此，由m+1方程可求得m+1个变量，于是可得方案的优先比pi。由此可据优先比的大小将方案排序，即量化了各方案的优劣关系。

3 案例及算法分析

用文献[14]的投资案例，用上述方法作决策分析。某投资银行对所控股的4家企业xi(i=1，2，3，4)进行投资评估，以便作为下一年的投资重点。评估指标有6项：t1为投资净产值率（纯产值与投资额之比），t2为投资销售率，t3为投资成本率（投资期内单位产品成本与其销售价之比），t4为投资利税率（纯利税与投资额之比），t5为环境污染程度，t6为社区服务状况，其中t1，t2，t4，t6是效益型指标，t3，t5是成本型指标，权重系数为（0.11，0.07，0.09，0.28，0.18，0.27）。设原始数据经定性指标量化得到数字决策矩阵A=(aij)mn如下：

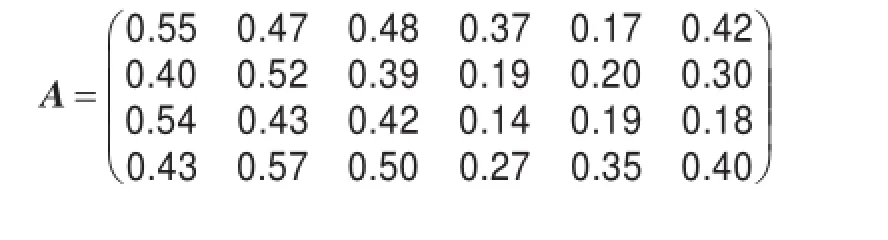
由此可得模糊决策矩阵：

计算方案的相对贴近度可得判别矩阵：

运用拉格朗日乘数法可计算出各方案的优先比：p1=0.523，p2=0.251，p3=0.089，p4=0.137，从而方案排序为x1＞x2＞x4＞x3，所以，首先考虑x1作为投资重点。

4 结束语

在文献[14]中，上述投资案例的方案排序为x1＞x4＞x2＞x3。尽管方案x1都是最优，但不同的决策方法，会对方案的排序产生差异，且对模糊条件下的多目标决策问题，有许多决策方法可供选择，因此，在何种情况下采用何种决策方法是一个必须考虑的问题，关于这个问题将另文探讨。

[1]Zadeh L A.Fuzzy sets[J].Information and Control，1965，8（3）：338-356.

[2]Gau W L，Buehrer D J.Vague sets[J].IEEE Transactions on Systems，Man and Cybernetics，1993，23（2）：610-614.

[3]范九伦.Vague值与Vague集上的贴近度[J].系统工程理论与实践，2006，26（8）：95-100.

[4]贾伟.一种基于未知度的Vague集相似度量新方法[J].计算机工程与应用，2012，48（27）：45-48.

[5]王万军，李恒杰，胡建军，等.一种Vague值转化Fuzzy值的偏联系数方法[J].计算机工程与应用，2013，49（1）：134-136.

[6]彭祖明.Vague集的Fuzzy集分解论[J].西南师范大学学报：自然科学版，2012，34（4）：118-122.

[7]刘盛辉，王伟，彭进业.不同Vague集相似度量直接聚类算法比较[J].中国科技论文，2013，8（1）：41-46.

[8]石玉强，王鸿绪.关于Vague集的相似度量定义的注[J].计算机工程与应用，2012，48（32）：129-131.

[9]崔春生，吴祈宗.基于Vague集的内容推荐算法研究[J].计算机应用研究，2010，27（6）：2109-2111.

[10]李瑞岚，黎昌珍，梁家荣.基于Vague集理论的多目标决策方法[J].广西大学学报：自然科学版，2012，37（6）：1267-1272.

[11]陈岩，张宁，陈侠.基于Vague集信息的多属性群决策专家水平评判方法[J].数学实践与认识，2013，43（1）：167-176.

[12]刘阳丽，杨爱萍，戴文战.基于区间值Vague集多属性决策的Topsis方法[J].浙江理工大学学报，2012，29（3）：370-373.

[13]陈蓉素.欧氏范数的Vague多目标决策[J].计算机工程与应用，2008，44（36）：219-220.

[14]符海东，雷大江.区间值加权模糊推理方法[J].计算机工程与应用，2005，41（6）：57-59.

[15]周文坤.模糊偏好下多目标决策的一种客观赋权方法[J].上海大学学报：自然科学版，2004，10（4）：410-412.

CHEN Rongsu

Center of Network and Information,Ningbo University of Technology,Ningbo,Zhejiang 315211,China

In Vague multi-objective decision-making research,the pairwise comparison decision behavior is proposed. The problem of the discriminant consistency is solved by Lagrange multiplier method and best choice is obtained.An example shows that the proposed method is effective and feasible.

multi-objective decision making;Lagrange multiplier method;sequence

在Vague多目标决策的研究中，引入两两比较决策行为，并通过拉格朗日乘数法解决一致性问题，最终找到最优方案。案例验证了该方法的有效性和可行性。

多目标决策；拉格朗日乘数法；排序

A

TP18

10.3778/j.issn.1002-8331.1309-0169

CHEN Rongsu.Algorithm study for multi-objective Vague decision making.Computer Engineering and Applications, 2014,50（18）：67-69.

陈蓉素（1972—），女，副教授，主要研究方向：计算机应用、模糊推理与决策。E-mail：crs1225@163.com

2013-09-12

2013-11-21

1002-8331（2014）18-0067-03

CNKI网络优先出版：2014-01-26，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1309-0169.html