BPF 重建算法的 CUDA 并行实现

伍绍佳陈 皓廖 丽桂建保

1(肇庆广播电视大学 肇庆 526060)

2(中国科学院深圳先进技术研究院 深圳 518055)

BPF 重建算法的 CUDA 并行实现

伍绍佳1陈 皓2廖 丽1桂建保2

1(肇庆广播电视大学 肇庆 526060)

2(中国科学院深圳先进技术研究院 深圳 518055)

反投影滤波(Backprojection-Filter，BPF)算法凭借其可实现感兴趣区域重建的优点，近年来逐渐被应用到锥束 CT 中。但是，由于算法的复杂性，实践中存在耗时问题，同时其 GPU 加速的实现亦存在显存不足等问题。因此，文章提出了一种基于 CUDA 的 BPF 并行加速算法。通过设计高效的算法框架，在保留其重建精度的前提下，有效地减少所需显存。此外，总结了正投影算法及 BPF 算法中采用的加速策略，如利用算法特征加速等，并引入显存池的概念优化算法架构。仿真实验结果表明，在精确重建的前提下，采用新框架重建 512×512×512 数据只需 8.055 s，感兴趣区域重建只需 4.566 s，只需 1.523 s 便可输出第一部分数据，且能把显存占用从 2.5 GB 减少到 100 MB 以下，适用于大数据重建。

反投影滤波算法；锥束 CT；感兴趣区域成像；图形处理器；图像重建；并行计算架构

1 引 言

自 1971 年第一台 CT 安装以来，CT 已经经历了几代的发展。近年来，锥束 CT 已经成为医疗诊断和放疗技术的重要工具，因此，如何提高锥束 CT 的性能是近年来研究的热点之一。 针对 CT 的性能，剂量、图像重建速度及图像质量是其重建的三个主要评判标准[1]。本文主要解决图像重建的速度问题及其在 GPU 应用过程中涉及的显存问题。近十几年来，解析法重建凭借其高效性得到大量的研究，与常规解析算法相比(如 FDK[2]等滤波反投影算法)，反投影滤波(Backprojection-Filter，BPF)算法[3,4]凭借利用较少量的投影数据重建出精确的图像，得到学者的广泛认可。凭借感兴趣区域扫描和重建，BPF 算法可实现降低剂量的目的，但其实现过程还存在运算量大等问题。故本文提出一个基于 CUDA 的BPF 算法加速架构，旨在更好地将 BPF 算法应用到实际中。

GPU 凭借其强大的并行计算能力使不同的CT 重建算法得以发展。其中，传统经典的 CT 重建算法，如 FDK 算法和迭代算法的并行加速模型[5,6]已经得到广泛的研究。而有关 BPF 加速的研究并不多，因此，本文着重于 BPF 的算法加速。根据文献搜索，Zheng 等[7]设计一个应用于GPU 中通用 Pi 线选择的方案，但是并没有详细地介绍如何利用 GPU 进行优化计算。此外，Zou等[8]曾提出基于 GPU 的 BPF 算法优化方案，尽管时间得到大幅度的提升，但是其架构并不是最优，如在大数据问题上并不能很好地应用或在实际应用中存在显存使用过多的问题；同时，由于其框架基于多 GPU，因而难以在商业项目中进行应用。除此之外，大部分相关研究也仅仅关注重建速度的优化，并没有考虑显存的合理利用，因此，本文引入显存池的概念去优化显存的管理。根据 BPF 算法的特性，本文首先提出适合实际应用的单 GPU 优化框架；其次对 CUDA 实现过程中采用的优化策略进行总结；最后，本文将阐述如何利用 GPU 进行 Shepp-Logon 模体投影数据的快速生成。

2 BPF 算法介绍

近年来，BPF 算法得到很大的推广，其原型由潘晓川小组在 2004 年以三维重建的形式提出，后来又提出其扇束模式。Yu 等[9]在 2008 年提出基于圆周轨迹的 BPF 算法，进一步地完善其在锥束 CT 的应用。如图1 所示，本文处理的投影数据亦为基于圆轨迹扫描获得。

BPF 算法是一个基于弦的反投影滤波重建算法。如图2 所示，弦被定义为射线源两点间的连线，即和，因此，沿着弦的单位向量可以表述为：

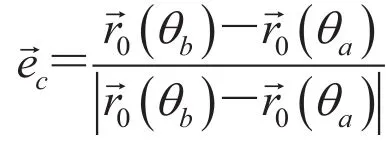
该弦上所有点可以描述为：

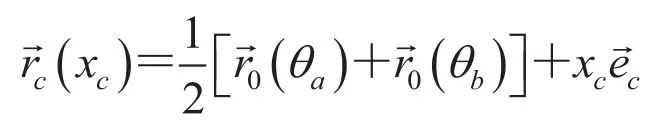
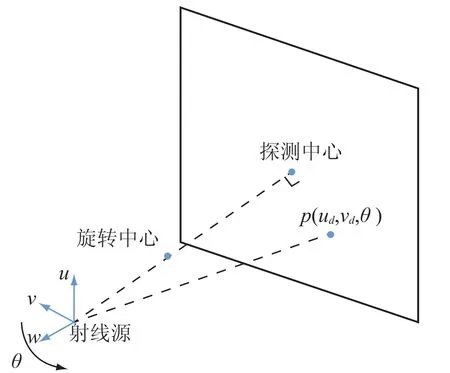
图1 BPF 算法几何扫描图Fig.1. Scan geometry of BPF

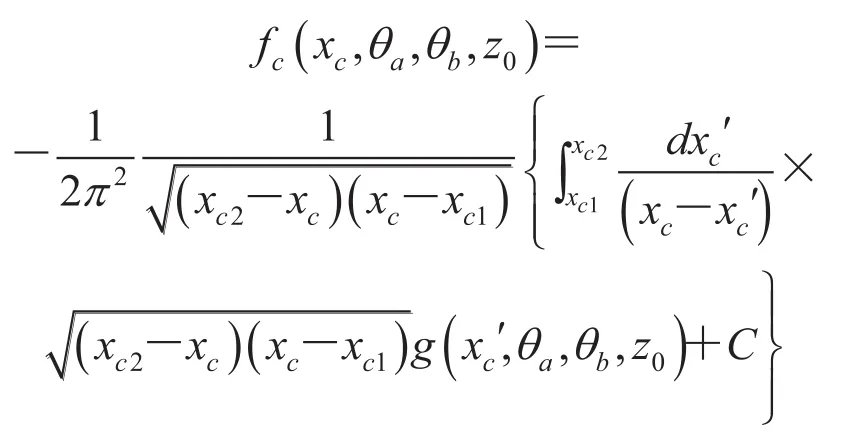
反投影部分可以描述为：

而边界项 C 则可以表达为：

P0是 X 射线经过 Pi 线中间点的投影数据平均值。

综上所述，BPF 算法的实现可以分解为以下5 步：

(1)对加权的锥束数据进行求导；

(2)沿着弦对加权后的投影数据进行反投影；

(3)对反投影后的数据进行滤波；

(4)计算边界项进行补偿；

(5)累加边界项和滤波后数据，并将结果乘以相关系数。

3 基于 CUDA 的 BPF 算法优化方案

GPU 作为辅助处理器，专门为协助 CPU 进行通用科学和工程计算而设计。接下来，本文首先针对模拟数据的生成进行介绍并提及其加速方法，随后详细介绍基于 CUDA 的 BPF 算法新框架，最后介绍在 CUDA 实现过程中采用的加速策略。

3.1 正投影数据的生成

重建算法的鲁棒性一般由其重建模体的精度来进行验证，因此，获得模体的投影数据是验证算法的必要条件。接下来，结合 GPU 简单地介绍本文采用的正投方案。

Siddon 算法是 CT 算法中正投影的经典算法。尽管该算法极大地保证其准确率，但是该算法耗时长，在实际应用中的效率并不高。因此，本文结合 Nvidia 公司的 sdk 例子[10,11]，对原有的投影算法进行优化，得出本文的正投影算法。

Sidon 算法把将投影物体看作一个三维网格，通过连接射线源与探测器相应像素点，求出该连线与其经过每个小方格上的入射点与出射点，计算其穿过的距离，整理为一个系统矩阵，然后再通过插值求出网格的灰度值，最后累加并获得探测器上每一点的投影值。但是，由于此方法需要计算每一个网格的穿过距离，并不能很好地进行加速。因此，如图3 所示，本文选择只计算穿过整个大网格的入射点和出射点，然后根据需要，以特定的步长把两点间的连线进行划分，并利用三维线性插值计算每段的灰度值，最后累加获得平板该点的投影值。

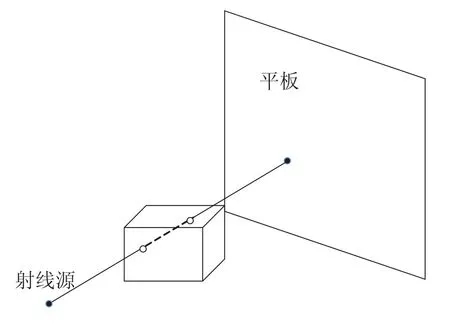
图3 正投影解释图Fig.3. Introduction of projection algorithm

在 GPU 端，数据读入后，以每条射线为一个线程，如探测器像素个数为 512×512，可以设512×512 的线程。不同射线划分的段数并不一致，每个线程计算该射线线段组的累加值，而线段的累加值则通过把物体映射到三维纹理内存上获得。选择三维纹理显存有两个原因：(1)由于此类显存获取为随机存取，纹理显存能优化读取速度；(2)纹理显存提供三维线性插值。加速后的正投影方案在保证投影计算质量的前提下，其计算速度大幅地提升。此外，根据原始数据的不同大小，可以把上述原始数据划分为若干块，每次只读取一块进行计算，并将计算值存于平板数组，进而进行下一数据块的计算，这样可以解决由于模体数据量大导致显存不足的问题。

3.2 BPF 算法实现

Zou 等[8]曾提出一个基于 GPU 的 BPF 算法框架，但其框架具有一定的局限性。由于医生对图像质量要求的提高，512×512×512 的图像重建往往不能满足其需求。同时 BPF 算法在原有的框架下需要很大的显存，以致在实际应用中要选用两个GPU，这样在实际应用中势必增加项目的成本。

根据上述算法讨论，BPF 算法在实现中遇到两个问题：(1)计算反投影过程慢；(2)所需存储空间大。而计算量大是 CT 重建一直存在的问题，且由于 BPF 算法需要计算边界项，其所需存储空间为原本算法的两倍，从而增加 BPF 算法实现的困难。

3.2.1 基于 CUDA 的 BPF 框架

如上所述，许多现行的框架都选择把每一个重建点的计算分配给每一个线程，如为512×512×512 的数据开辟 512×512×512 个线程去进行反投影，但是此方法在 BPF 算法中存在严重的显存问题。因为其不仅要保留512×512×512 的反投影数据，还需要保留相关的边界项，因此，需要设计一种在一般 GPU 上能运行并计算速度快的算法框架。

如图4 所示，首先从 CPU 端读入数据并存入 GPU 端，然后根据公式对投影数据进行求导；接着对重建层进行分块，根据重建的不同块所需的投影数据，导入相应的求导数据，并对该块进行反投影(包括计算该块的反投影值和其边界项值)；反投影后再进行滤波，滤波后将该层数据和边界项数据进行累加，这样一段数据块重建完成并输出到终端，遍历完所有重建块后，则完成整个重建。此流程的优点如下：

(1)可扩展性。由于实际应用中不仅进行重建处理，还可能在其中加入降噪等校正操作，若重建处理占据所有显存，则大大地降低算法的灵活性。

(2)显存空间使用少。新框架中只需要反复利用同一块显存，不需要同时保留整个重建体数据及其边界项数据，其分析见下节。

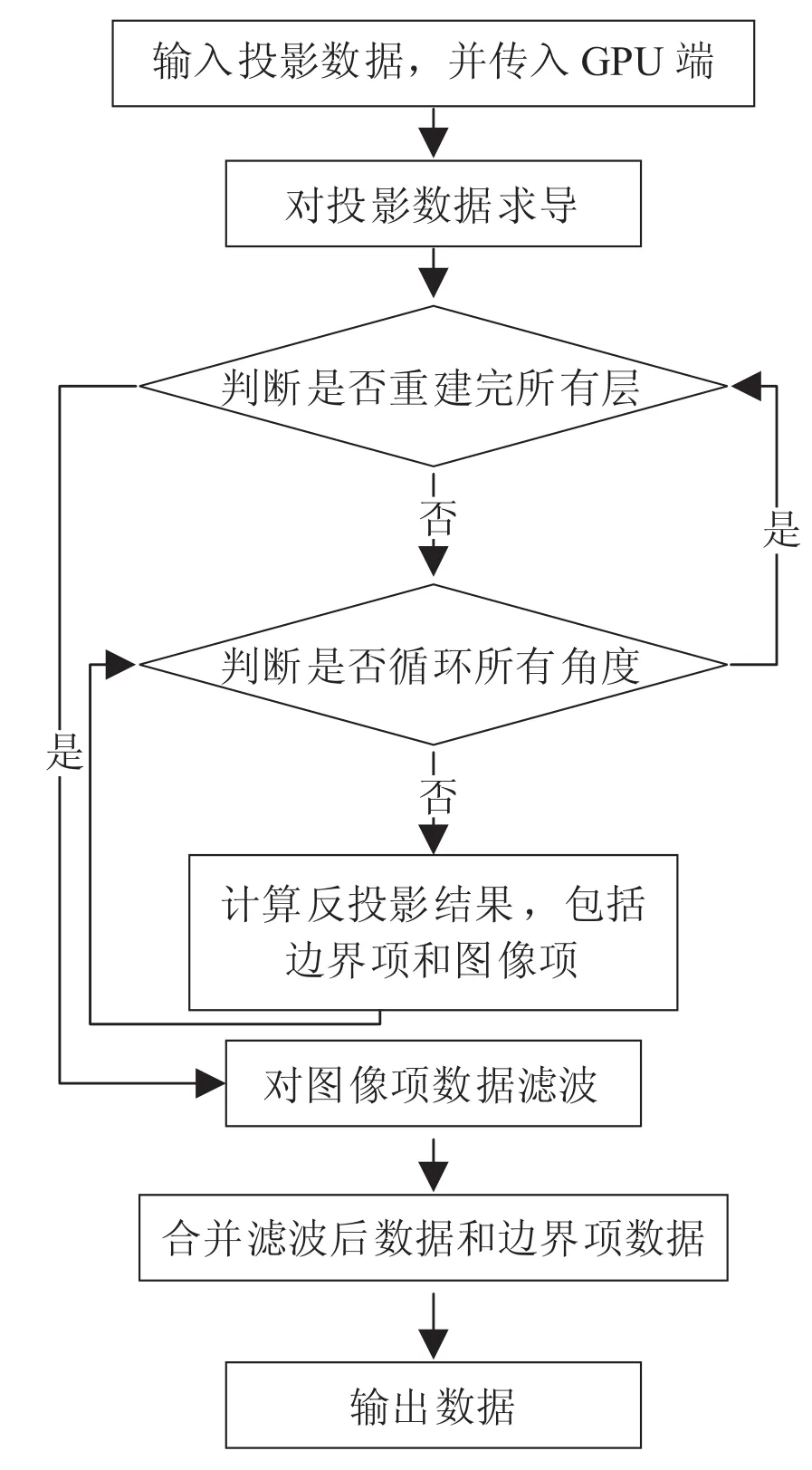
图4 基于 CUDA 的 BPF 算法新框架Fig.4. Frame of BPF algorithm based on CUDA

(3)输出快。重建一块数据块后便可输出，并不需要等待所有数据重建完再进行输出，因此在实时性上，此框架比旧方法更为优越。

此外，需要说明以下两点：首先，此框架并不需要担心过度地进行纹理绑定，因为绑定并不是把数据重新传输，只是绑定指针，所以内部循环并不会大量提升计算时间。因此，算法实现过程中，虽然涉及纹理内存的不断映射，但由于其只把相应指针进行映射，并不会占据过多的时间；其次，虽然进行一次 512×512×512 的数据重建处理的时间比目前分段处理的时间短(因为新方法需要不断地开启 kenel 函数)，但是，由于每一块数据块处理的数据量大，并已超过一次能同时处理的数量，即所有 SM 一次处理的线程数。所以，与一次处理相比，新方法所用的时间并不会大大的增加，而其降低显存空间占用的优势则较旧方法优越。

3.2.2 新框架内存分析

根据图4 所示，Zou 等[8]需要存储整个重建空间的数据，并将其累加，其中包括图像项和边界项数据，过多地开辟显存容易导致其他操作无法进行。新框架下只需要一块重建块的显存空间，可以省略大部分图像项和边界项数据的空间。以下为简化的内存分析：

设投影数据大小为 M×M，角度为 T，一般重建的大小与投影数据的大小相仿，设为 P×P×P，假设 P 为 2 的幂次方(一般 P 为512)，由于含有图像项，边界项及合并项三部分，因此所占空间大小为 3×P×P×P。在滤波过程中会产生频域数据，其长度一般为其最接近的 2 的幂次方，以保证其精度，假设为2×P×P×P，因此，原方案为：

Memory＝M×N+5×P×P×P由于本架构把重建层数进行分块，每一块的层数为 H(其大小可以根据实际需要进行控制)，因此总的显存需求为：

Memory＝M×N+5×P×P×H由公式可以看出，在显存的利用上，新框架有绝对的优势，新架构所需空间仅为 Zou等[8]的 H/P，从而方便其他处理的进行。若为512×512×512 的数据，以 16 层数据为一数据块，所需显存空间仅为原方案的 0.03125 倍，即需要不到 100 Mb 的显存(考虑到其他辅助变量的存储)。因此，在大数据重建下，新框架的优势尤其突出，使其在重建数据量大的情况下能保证程序正确性的同时不影响其他操作。

3.2.3 显存的统一管理

由于对重建层进行分块，程序会增加对显存的申请和销毁，这样，由于申请内存块的大小不定，频繁使用时会造成大量的显存碎片进而降低性能。本文对内存池的思想进行简化，并应用至重建算法的显存管理上。由于重建算法的显存需求是固定的，因此，针对不同病人的图像处理也是固定的，所以只需在程序开始时分配固定大小的显存空间即可。

其显存管理机制如下：首先，在不影响其他操作的情况下，根据不同机器的显存空间进行一次性分配。申请整块显存空间后，根据不同的处理，选择合适的计算单位进行显存的申请和释放。如果每次申请空间过小，将对显存进行多次申请而影响算法的整体性能；若每次申请过大，则申请的显存量会超出允许范围。因此，本文根据上述内存分析进行分块的自动计算并自动分配显存空间。这样，向显存池申请显存比直接向系统申请快，且不会产生碎片，在实际应用中效果显著。

3.2.4 CUDA 相关加速策略

由图4 可看出，反投影滤波可以大致划分为反投影、滤波、输入输出三部分，接下来根据不同部分介绍适用于 BPF 算法的加速策略。

(1)反投影部分

反投影部分包括图像项和边界项的计算，是整个重建耗时最长的部分。由于其存在随机存取的现象，因此把全局内存的数据映射到纹理内存可以大幅减少读取数据的耗时，而二维纹理的利用也可比一维纹理优化 1/3 左右的时间；此外，如 Zou 等[8]提及的，在反投影中需采用预判策略，即由于 BPF 算法是采取感兴趣区域重建的策略，如果只需重建部分区域，可以提前进行检测从而减少不必要的反投影，此方法能大幅度地减少重建时间；BPF 算法涉及较多辅助变量，这些变量数量较多且不同重建点具有不同值，因此不便存储于常量存储器，但其在不同层上的值一致，因此本文采取计算一次并存储于全局内存的策略，减少不必要的计算。

(2)滤波部分

BPF 算法的滤波为希尔伯特滤波，与 FDK 算法的 Ramp 滤波器优化方案基本一致。本文利用CUFFT 库对傅里叶变换进行加速优化，在新框架下，它的批处理特点不再是投影数据的批处理，而是图像数据块的批处理。在新框架下可以扩展出许多模型，可以选择一次滤波两层或更多，这样，批处理的特点也可进行最大化的利用。

(3)输入输出部分

由于新框架是一块块输出重建数据，本文把合并过程归入输入输出部分中。从 GPU 拷贝到CPU 的时间基本可以完全隐藏。通过创建不同的流：一个进行运算，另一个则用来进行数据输出。这样一层计算完成后，可以通过输出流把传输时间隐藏，再通过在 CPU 中开辟新的线程把获得的数据输出到硬盘，这样可以最大限度的缩短输出时间。

4 数据实验结果和分析

为了验证算法的有效性，本文设计了 2 个测试方向：(1)重建的准确度；(2)重建的耗时。测试模体为三维的 Shepp-Logan 模体，重建规模为 512×512×512。测试平台为 3.2 GHz Intel Core(TM) i5-3470 双核 CPU，16 GB 内存，Nvidia GeForce GTX660 Ti 显卡；开发环境为Visual Studio 2010，cuda5.5 runtime API；模拟放线的几何环境分别为：射线源到探测器距离为700 mm，射线源到旋转中心的距离为 350 mm，探测器间距为 0.1 mm、长宽均为 51.2 mm，Shepp-Logan 模体的大小为 512×512×512，采样间隔为 0.05 mm。

4.1 准确性比较

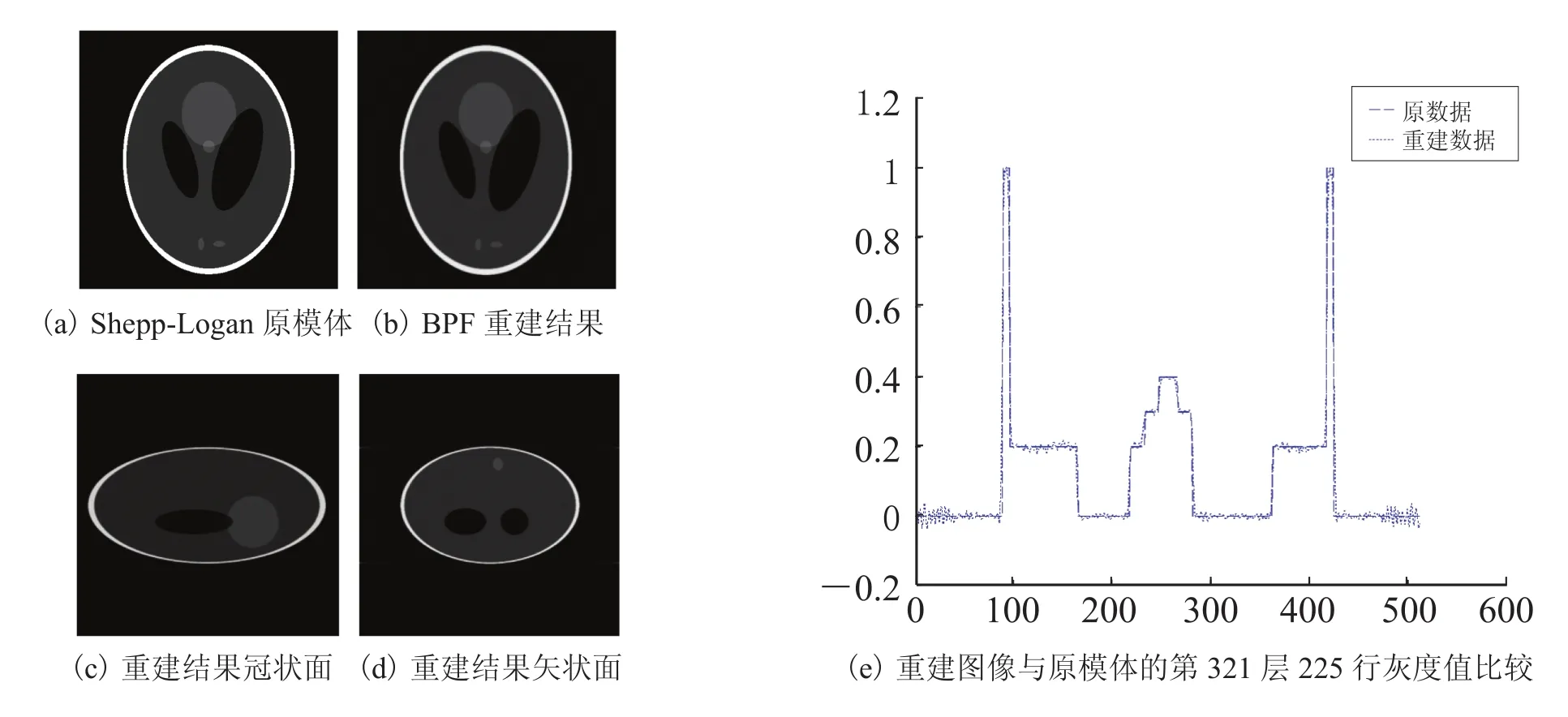
图5 采用 Shepp-Logan 模体重建的不同截面断层图像Fig.5. The reconstructed slice images of Shepp-Logan phantom from different sections

图5(a)和(b)分别为原图及 GPU 重建结果的切片方向图像比较；而图5(e)则为第 321 层中第 256 行的灰度值曲线比较，结果显示重建数据与原数据变化规律基本上一致，误差在容忍范围内。由于本实验为三维重建，圆周轨迹下的扫描结果都是近似重建，图5(c)和(d)分别为重建物体冠状面和矢状面的结果，结果基本符合小锥角情况。综上分析，新框架在精度上满足需求。

4.2 时间比较

由于不同研究小组所采用的机器不一致，导致获得的重建时间的可比性不高，如 Zou 等[8]的配置为专门进行科学运算的 Tesla 双显卡。因此，本文结合 Zou 等[8]的架构进行改写并作为比较。通过比较各部分的计算时间，分析不同架构下的性能，每个测试数据通过 NVIDIA 公司提供的 Visual Pro fi ler 获得，每个数据在测试 10 次后取平均值。如表1 所示，Zou 等[8]的架构与本文的架构时间上相差不大，但本文所用架构显存的消耗不到 100 MB，大大地减少显存的消耗。因此，在实际应用上提供极大的方便，如实际应用中往往需要额外的显存空间进行校正处理等。

本文架构可以将重建层划分不同块数，因此，第一块重建完成后可以直接输出到用户界面上。在本次试验中，16 层为一组，仅需 1.523 s便可从界面上获得重建数据。BPF 算法的另一个优点在于其感兴趣重建，若重建 512×512×256数据则只需要 5.609 s。

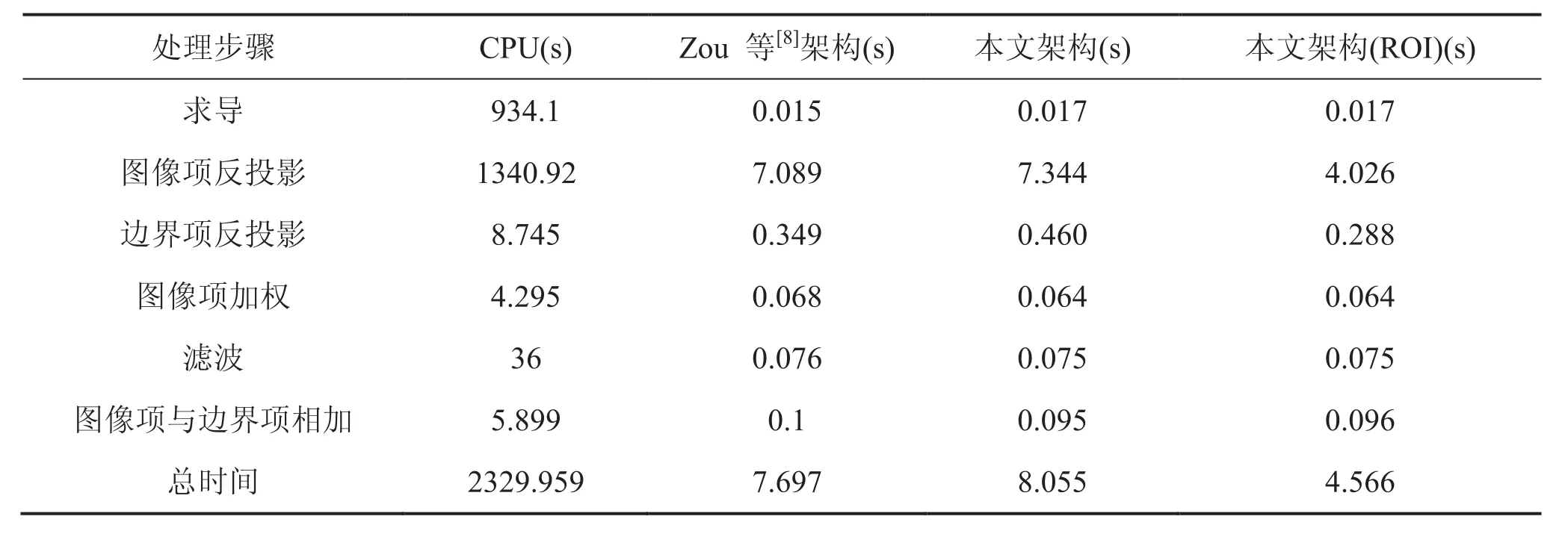
表1 本文结果与最新研究结果比较Table1. Result comparison between this paper and the latest outcomes

表2 不同大小的重建结果比较Table2. Comparison of reconstruction results based on different size

此外，表2 为新架构在不同重建大小下的性能比较，其中 1024×1024×128 与512×512×512 是重建空间大小一致的比较。根据结果所示，本方案能在不改变架构下适用于不同大小的图像重建，不需要根据不同大小而改变重建策略。

最后，针对 3.2.2 所述，实验测得新方案能把重建 512×512×512 的显存消耗由 2.5 GB 减少到 100 MB 以下，证明其适合大数据的重建。

5 结 语

随着 GPU 在科学计算的广泛使用，CT 重建算法计算耗时长的问题得以解决。本文提出一种更优于以往研究结果的基于 CUDA 加速的优化架构。本文设计的新架构采取以下策略：(1)合理的显存利用，在充分利用 CUDA 核心的前提下，对显存进行复用；(2)利用 BPF 算法的特点进行速度优化；(3)对常用数据进行预先计算。实验结果显示，只需要不到 100 MB 的显存，实现重建 512×512×512 数据只需 8.055 s，第一块数据块输出仅需 1.523 s，而感兴趣区域重建为 4.566 s。实验证明，新的架构在不损失 BPF 算法原有精度和保证速度大幅度降低的前提下，只需要较少的显存空间进行重建，为实际应用提供一个高效的计算框架。

[1] Jung KJ, Lee KS, Kim SY, et al. Low-dose, volumetric helical CT: image quality, radiation dose, and usefulness for evaluation of bronchiectasis [J]. Investigative Radiology, 2000, 35(9): 557-563.

[2] Feldkamp LA, Davis LC, Kress JW. Practival conebeam algorithm [J]. Journal of the Optical Society of America A: Optics, Image Science, and Visions, 1984, 1(6): 612-619.

[3] Pan XC, Zou Y, Xia D. Image reconstruction in peripheral and central regions-of-interest and data redundancy [J]. Medical Physics, 2005, 32(3): 673-684.

[4] Cho S, Bian J, Pelizzari CA, et al. Region-ofinterest image reconstruction in circular cone-beam microCT [J]. Medical Physics, 2007, 34(12): 4923-4933.

[5] 韩玉, 闫镔, 宇超群, 等. 锥束 CT FDK 重建算法的 GPU 并行实现 [J]. 计算机应用, 2012, 32(5): 1407-1410.

[6] 雷德川, 陈浩, 王远, 等. 基于 CUDA 的多 GPU加速 SART 迭代重建算法 [J]. 强激光与粒子束, 2013, 25(9): 2418-2422.

[7] Zheng H, Yu YY, Kang Y, et al. Investigation on PI-line selecting method based on GPU accelerated backprojection fi ltered VOI reconstruction [C] // Medical Imaging 2010: Physics of Medical Imaging, 76222G, doi:10.1117/12.839831.

[8] Zou J, Chen H, Zhang QY, et al. Fast Cone-beam CT image reconstruction based on BPF algorithm: application to ortho-CT [J]. International Journal of Computational Methods, 2013, doi: 10.1142/ S0219876213500679.

[9] Yu LF, Zou Y, Sidky EY, et al. Region of interest reconstruction from truncated data in circular cone-beam CT [J]. IEEE Transactions on Medical Imaging, 2006, 25(7): 869-881.

[10] NVIDIA Corporation. NVIDIA CUDA Programming C Guide, Version 5.5. 2013 [OL]. http://www.nvidia.cn/object/cuda-cn.html.

[11] 张舒, 褚艳利, 赵开勇, 等. GPU 高性能运算之CUDA [M]. 北京: 中国水利水电出版社, 2009. Science, 2012, 336(6085): 1171-1174.

CUDA Based Parallel Implementation of BPF Algorithm

WU Shaojia1CHEN Hao2LIAO Li1GUI Jianbao2
1( Zhaoqing Radio & Television University, Zhaoqing 526060, China )
2(Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China )

Based on its region-of-interest (ROI) reconstruction advantage, backprojection-filter algorithm has been used in cone-beam CT recently. However, because of its complexity and computation, there is memory insufficiency in the implementation of GPU acceleration. Hence, CUDA-based parallel implementation for BPF algorithm was proposed. Meanwhile, an accelerated projection scheme and other accelerated techniques were included as well, such as features of BPF for acceleration. Besides, video memory pool was introduced to optimize the implementation. With an ef fi cient structure, the simulation results show that it takes only 8.055 seconds by using the new structure to reconstruct 512×512×512 data and only 4.566 seconds for the ROI reconstruction. The output of fi rst block data takes only 1.523 seconds. With a great decrease of memory occupation from 2.5 GB to less than 100 MB, the new scheme is suitable for big data reconstruction.

backprojection-filter algorithm; cone-beam computed tomography; region of interest imaging; graphics processing unit; image reconstruction; parallel computing architecture

TP 391.41

A

2014-06-18

国家科技支撑计划(2012BAI13B04)；国家自然科学基金(61102161)；深圳市项目(JCYJ20130401170306796, JC201105190923A)

伍绍佳，硕士，讲师，研究方向为计算机应用与网络技术；陈皓，硕士研究生，研究方向为 CT 重建与加速算法；廖丽，硕士，讲师，研究方向为软件技术应用；桂建保(通讯作者)，博士，高级工程师，研究方向为 X 射线与 CT 成像技术，E-mail：jb.gui@siat.ac.cn。