一种磁性目标定位跟踪系统的标定方法

胡 超任宇鹏,2王文虎宋 霜冯忠晴,2王永辉,2袁小英,2

1(浙江大学宁波理工学院信息科学与工程学院 宁波 315100)

2(太原科技大学电子信息工程学院 太原 030024)

3(宁波大学信息科学与工程学院 宁波 315211)

4(新加坡国立大学生物医学工程系 新加坡 119077)

一种磁性目标定位跟踪系统的标定方法

胡 超1任宇鹏1,2王文虎3宋 霜4冯忠晴1,2王永辉1,2袁小英1,2

1(浙江大学宁波理工学院信息科学与工程学院 宁波 315100)

2(太原科技大学电子信息工程学院 太原 030024)

3(宁波大学信息科学与工程学院 宁波 315211)

4(新加坡国立大学生物医学工程系 新加坡 119077)

文章磁目标跟踪系统选用霍尼韦尔 HMC1043 磁传感器阵列来采集永磁体的磁场信息，并实现定位。由于磁场传感器阵列的各传感器位置、方向和灵敏度直接影响系统定位的精确度，所以要求对这些磁传感器参数进行准确的标定。文章针对磁传感器阵列的标定问题提出了目标误差函数和优化计算方法。通过对所有参数的迭代计算和优化更新使目标误差函数达到最小，完成对磁传感器的位置、方向和灵敏度等参数的标定。文章方法已对实际传感器系统实施应用。在 MATLAB 环境下，PC 机采集目标磁体的磁场信号，通过算法计算确定所有磁传感器的位置、方向和灵敏度，完成标定。通过文章方法的标定，系统定位精度有明显的提高，本方法的可行性和合理性也因此得到验证。

永磁体定位；磁传感器阵列；位置与方向；灵敏度系数

1 引 言

无线胶囊内窥镜自 2000 年诞生以来，已经在肠胃道检查中得到应用[1]，且呈现不断增长的趋势。目前的胶囊内窥镜存在两大问题：一是如何使其运动受医生的操控，以实现有针对性地对肠胃道组织进行详细的观测；另一问题是如何提供胶囊内窥镜在胃肠道中的位置信息，以及发现的病变组织尺寸信息[2]。要解决这两问题，需要获取胶囊内窥镜相对于胃肠道环境的位置、方向和运动信息。也就是胶囊内窥镜的定位。

一个合理的胶囊内窥镜定位方法是基于磁场信息。将永磁体嵌入胶囊，其在人体内肠胃道内运动时，可在周围产生磁场分布的变化。永磁体在三维空间中，有 3 个位置参数；并在其主轴上形成磁场方向，有 2 个方向参数。所以，磁体运动时，有 5 个位置和方向参数，也就需要至少 5个磁传感器进行检测，才能建立 5 维方程组。之后再用合适的定位算法来计算求解出 5 维位置方向参数，追踪无线胶囊内窥镜在肠胃道的位置和姿态信息[3,4]。

我们提出对胶囊内窥镜的磁体进行检测的传感器阵列及相应的计算算法[5,6]。磁场传感器阵列采用一定数量(5 个以上)的三轴磁场传感器，根据人体的特点固定在一个穿戴式架子上，最终使其分布于人体四周。定位前，要知道传感器的位置、方向和灵敏度，才能应用算法计算胶囊磁体的位置和方向参数[7,8]。由于传感器的安装要适合人体的架子，其位置和方向无法精确测量，而且传感器有一定尺寸，其中心位置可能有偏差。另一方面，由于磁传感器生产工艺存在误差，以及受其在硬件电路中布置的影响，各个传感器的灵敏度系数也不尽相同。传感器的这些参数直接影响系统定位的精确度，因此在定位之前，必须对胶囊内窥镜磁定位阵列系统建立三维坐标系，对各个传感器进行标定，准确获取它们的位置、方向和磁场灵敏度系数。

本文针对胶囊内窥镜磁场定位系统的标定进行讨论。首先讨论磁体磁场的模型和特点、系统的组成和算法及检测电路；进而介绍标定的目标函数、标定算法和实现程序；最后，针对实际的传感器阵列系统，让磁体处于已知典型空间位置点上，系统进行数据采集，并应用提出的算法获取所有传感器的位置、方向和灵敏度参数，实现准确标定。

2 磁定位系统组成

2.1 磁定位系统的总体设计

依据人体的形状，我们设计了穿戴式传感器阵列。32 个三轴传感器固定分布在椭圆形的架子上。如图1 所示，装置分四层，每层 8 个，可以套在人体腹部外周。内嵌永磁体的胶囊内窥镜在人体肠胃道内运动，分布在人体四周的磁传感器阵列通过检测永磁体磁场大小的变化，将磁场信号转换为电压信号。

磁定位系统的电路总体设计如图2 所示。其具体工作流程如下：传感器阵列采集永磁体的磁场数据，得到表征磁场强度的电压信号，通过 DG406 模拟选通芯片将其送入 ARM 处理器；ARM 自带的 16 位 A/D 转换模块将模拟电压信号装换为数字信号，同时控制 DG406 的通道选择，通过 TTL 转 USB 接口将数字信号送入 PC机；PC 机对数据做进一步分析处理，通过合适的算法计算永磁体的位置和姿态等信息。

磁定位系统的硬件设计如图3 所示。

2.2 磁场定位算法

对于空间一点 P，若磁铁的尺寸与磁铁到点P 的距离 R 相比非常小，那么可以把该小磁铁看成磁偶极子。如图4 所示，将轴向磁化的圆柱形永磁体置于三维坐标系中，其在空间中 Pl点产生的磁场强度[4]为：

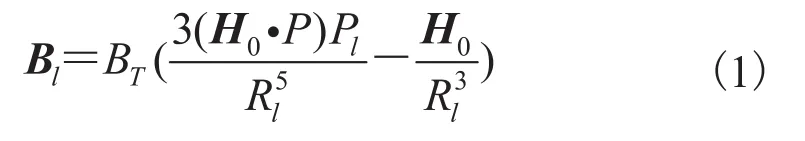
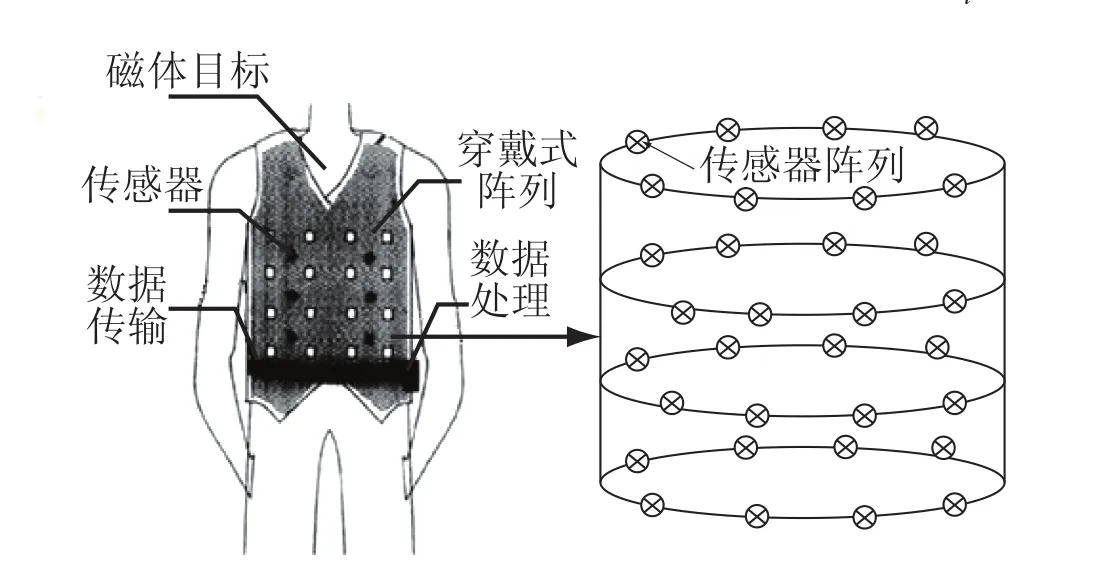
图1 穿戴式传感器阵列Fig.1. Wearable sensor array

图2 磁定位系统总体设计框图Fig.2. The overall design of magnetic positioning system

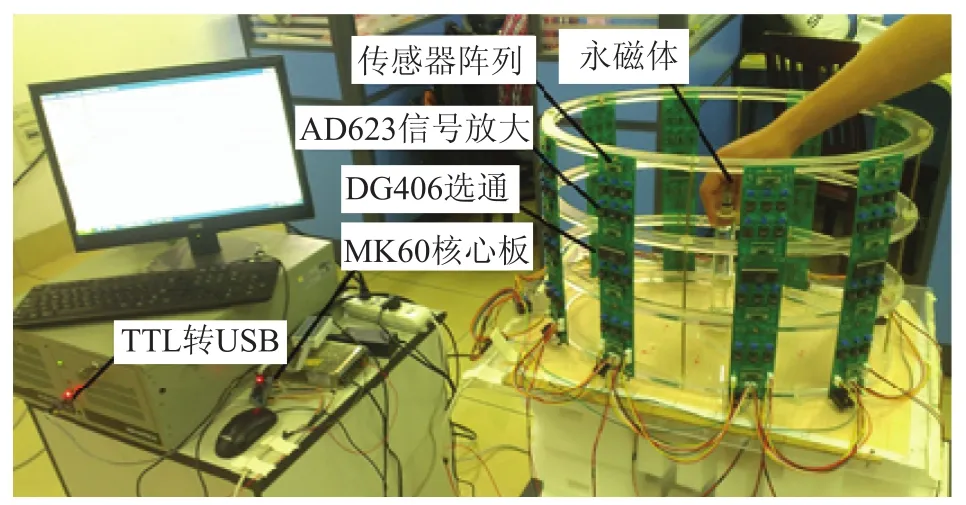
图3 磁定位系统Fig.3. Magnetic positioning system

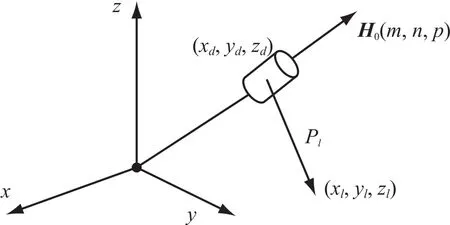
图4 轴向磁化的圆柱形永磁体(磁偶极子)模型Fig.4. Cylindrical axially magnetized permanent magnet model

其中，

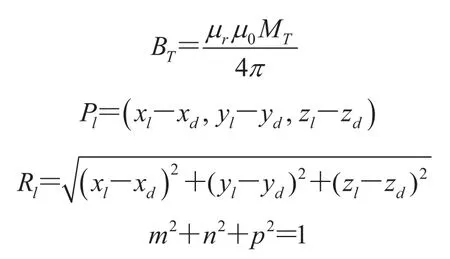
其中，(xd, yd, zd)为永磁体的位置坐标；H0＝(m, n, p)为永磁体的磁场方向；(xl, yl, zl)为 Pl点坐标。

将式(1)展开为 3 个正交方向上的分量(Bx, By, Bz)为：

上式中，磁感应强度(Bx, By, Bz)可以通过磁传感器得到，Pl点坐标(磁传感器)的位置已知，则通过上式可以计算得到永磁体坐标(xd, yd, zd)和永磁体的磁场方向(m, n, p)。

(2)～(4)式为非线性方程，可以采用非线性方程的求解方法求解。由于方向矢量大小可任意，我们加上限制条件，矢量模为 m2+n2+p2＝ 1。显然，需要 5 个以上不同位置 P 点传感器，即可形成五个方程，计算得到永磁体坐标(xd, yd, zd)和永磁体的磁场方向(m, n, p)[6,7]。

用三个方向轴正交的磁感应强度分量定义如下的目标误差函数：

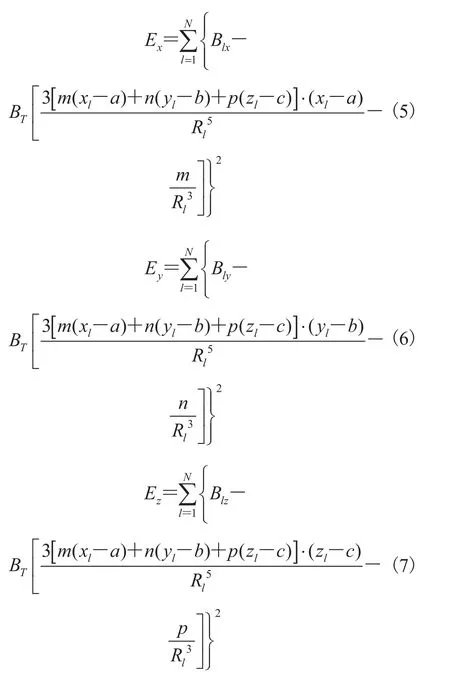
系统总目标误差就是以上三个误差之和：

利用式(5)～(7)，寻找最合适的位置参数(a, b, c)和方向参数(m, n, p)，使误差目标函数 E最小[7]。非线性方程最小问题可以通过非线性优化算法求解，如高斯-牛顿法、牛顿法、拟牛顿法、共轭梯度法、粒子群 PSO 算法和 Levenberg-Marquardt 算法。

2.3 传感器与电路形式

我们选择霍尼韦尔 HMC1043 磁传感器作为磁场信号采集传感器，如图5 所示。该传感器是一种采用霍尼韦尔各向异性磁(AMR)技术的小型 3 轴表面安装传感器，适用于低磁场环境中，可以提供 3 个正交方向上的磁场强度值。其内部结构及引脚分布如图6 所示。

图5 霍尼韦尔 HMC1043 磁传感器Fig.5. The Honeywell HMC1043 magnetic sensor

图6 霍尼韦尔 HMC1043 引脚分布和内部结构Fig.6. Honeywell HMC1043 pin out and internal structure

2.4 信号放大电路

HMC1043 在+6 V 电压工作输出电压范围：±1.08 μV～±36 mV，仅在 mV 级别，电压太小不便于分析处理，故需将其放大。本文采用放大器 AD623 将该电压信号放大，AD623 工作于±6 V 双电源差分放大模式，放大电路如图7所示。

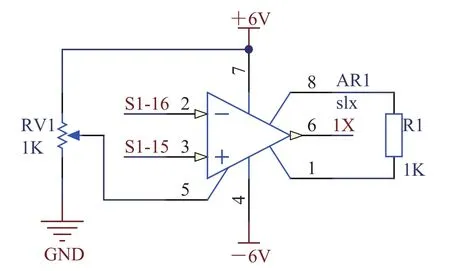
图7 AD623 放大电路Fig.7. AD623 ampli fi er circuit

放大倍数 A＝1+100k/2k＝51，这样放大器输出电压范围约为—1.8 V～+1.8 V。负电压不利于后期进行 AD 转换，所以需在 5 号管脚加上 1.8 V 参考电压将电压全部提升到 0 V 以上。放大后的信号经 6 号管脚输出至模拟选通芯片DG406。

2.5 多路通道切换电路

磁定位系统采用 32 个磁传感器进行磁场数据采集，每个传感器有 x、y 和 z 三个方向的数据，如此一来总共有 96 组数据要进行处理。数据量大，需对 AD 转换通道进行时分复用。本系统采用 8 路 AD 转换通道对 96 路数据进行采集，则每路 AD 需 1/12 时分复用。选取 DG406模拟选通开关对 4 个传感器(12 路信号)为一组的传感器进行选通，选通电路如图8 所示。

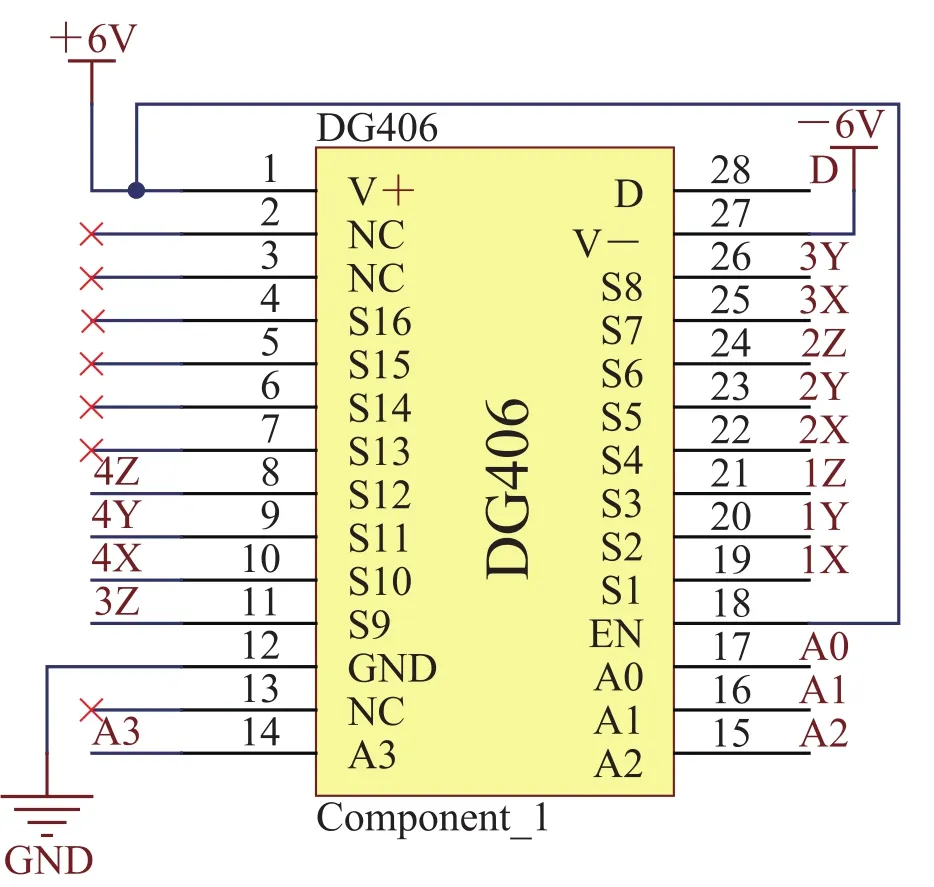
图8 DG406选通开关电路Fig.8. DG406 selector switch circuit

DG406 的输入端 S1～S12 依次连接 4 个传感器的输出端，选通后经 D 端输出至嵌入式模块。

3 标定方法

从上述的定位系统和定位方法可知，要进行定位，必须要知道各传感器的位置和对准的方向。同时，要知道每个传感器通道的灵敏度，并从检测的电信号换算出磁场强度，才能应用算法计算定位定向参数。所以，要实现对永磁体的精确定位，首先需要对传感器阵列的位置、方向及灵敏度系数等参数进行标定。

我们设计了一个标定平台，以对平面平台进行刻度。在标定过程中，可以准确测得永磁体(磁场源)的位置和方向，同时计算机能采集每个传感器的数据。根据永磁体目标的位置和方向信息以及各个传感器的数据，可以利用最优化方法，计算出各个传感器的位置、方向和灵敏度参数。

如图9 所示，我们用三种不同高度的标定杆， 将磁体放在杆上进行测试。每一高度层预设11个永磁体待测点，点的间距为 6 cm，每个点测量 x、y 和 z 三个不同姿态的数据(出于计算方便，分别取 H0为(1 0 0)、(0 1 0)和(0 0 1))，相当于每层测试 33 组数据；然后再根据整个模型的高度，选取高度分别为 10 cm、18 cm 和 25 cm的三层，这样一共测试 99 组数据。

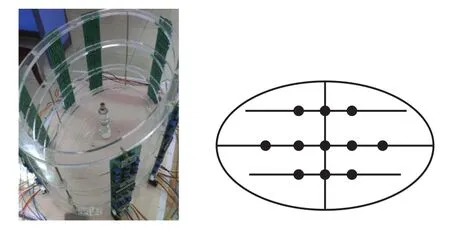
图9 永磁体采样点分布图Fig.9. The distribution of permanent magnet sampling points

定义为某磁传感器第 i 次采样在 3 个传感器轴线方向上输出的电压数据 ，而为换算至定义空间坐标系中的三轴电压信号数据。其映射关系为：

图10 传感器轴线方向与空间坐标系关系Fig.10. The relationship between sensors in the axial direction and space coordinate

其中，θ 为传感器轴线方向与空间坐标系之间的夹角，如图10 所示。传感器竖直安装，故其竖直方向(y 方向)与空间坐标系竖直方向(y 方向)夹角为 0。标定前需要对各个传感器的方向进行预估，下面介绍的方向校正步骤能准确地确定各传感器的方向参数。

(Vix, Viy, Viz)T和磁感应强度(Bix, Biy, Biz)T的关系可以表示为:

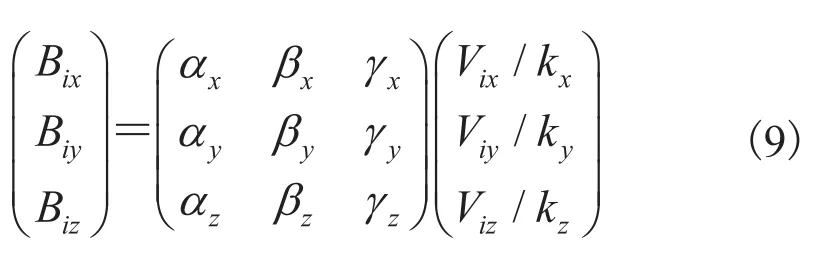
式中，(Bix, Biy, Biz)根据式(1)～(4)计算得到(为简化，省略了传感器序号 l)。

三轴磁传感器的灵敏度用 kx、ky和 kz表示。磁传感器的方向校正由矩阵实现，该矩阵表示为：

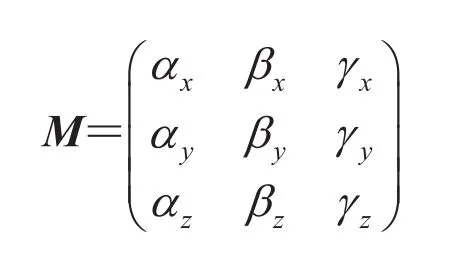
标定的目标就是准确确定灵敏度 kx、ky和kz，各传感器位置(x, y, z)和方向矩阵 M(这里，传感器序号被略去)。

3.1 传感器灵敏度标定

以 kx为例，定义误差函数

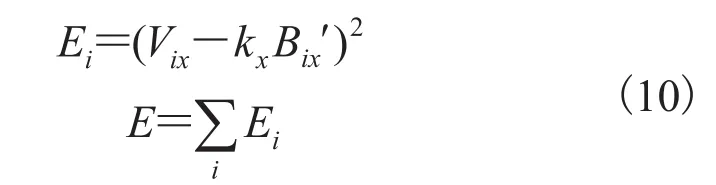
为使误差 E 最小，令

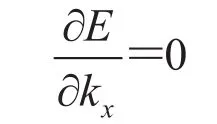
即得：

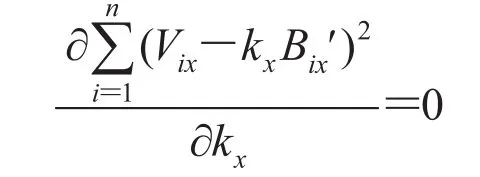
得到：

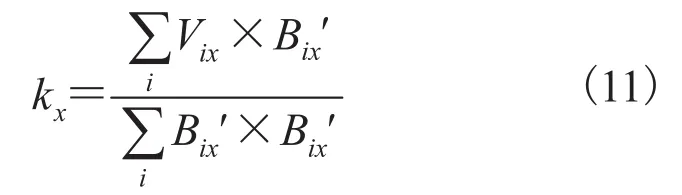
同理，有

3.2 传感器位置标定

进行传感器空间位置的测量时存在测量工具和人为读数的误差。故需对传感器位置进行校正，以提高测量的准确性。定义误差函数

调整传感器位置参数(x, y, z)，可使误差 E 最小，即优化选择各个传感器的对应位置(x, y, z)T。这是一个非线性最小二乘问题，用 LM 算法求解。

3.3 传感器方向标定

传感器内部芯片具有相应的坐标，但由于制作工艺存在误差，使得传感器轴 x、y、z 三个方向两两之间不完全正交，造成测量误差，影响磁场信号测量精度。式(10)展开得：

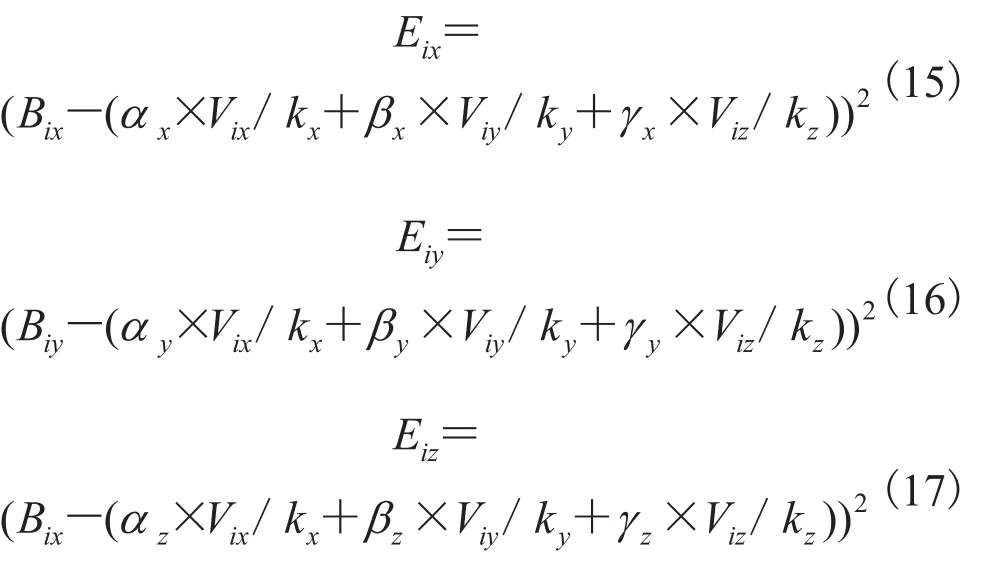
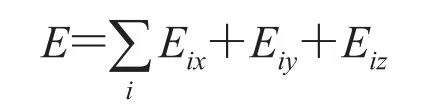
令误差 E 最小，即形成最小二乘问题。计算可得方向校正矩阵 M

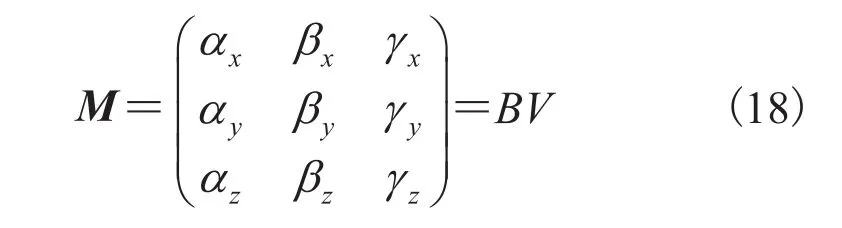
其中，

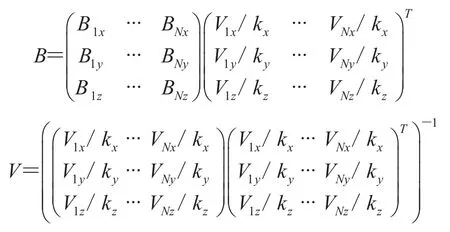
3.4 循环迭代获取参数

以上位置、方向和灵敏度参数对磁场强度是相互影响的。为此，要用迭代方法达到稳定解来寻求优化的参数。计算过程如图11 所示。

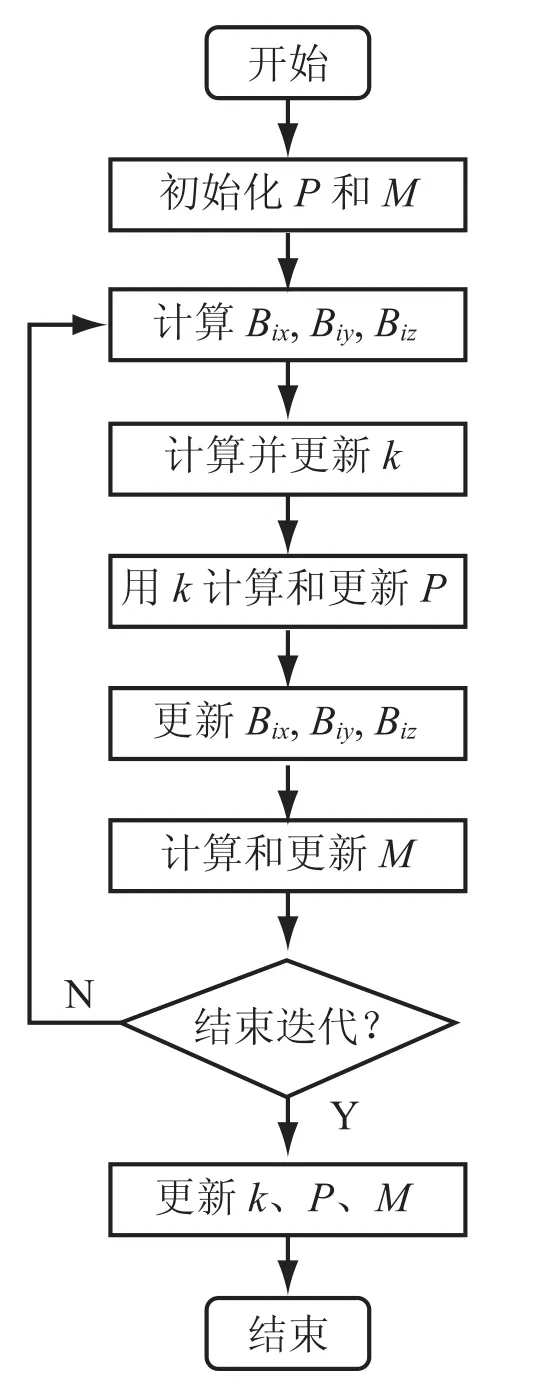
图11 标定流程图Fig.11. The fl owchart of calibration

4 传感器标定结果及标定前后定位精度的比较

4.1 传感器标定结果

选用嵌入式系统进行数据采集。该系统核心为 ARM Cortex-M4 内核，100 MHz 主频。选用其中 8 路单端 16 位精度 ADC 通道同时进行 AD转换，然后通过串口将 AD 采样的传感器数据发送至上位机。上位机通过 MATLAB 对数据进行分析计算，实现对传感器参数的标定。通过三个高度的标定杆，选取 3 层高度(y 坐标)，每层 11个点(x、z 坐标)，每点取三个姿态，共计采集99 组数据，对 32 个传感器进行在 x、y、z 三个方向的灵敏度、位置和方向的标定。

在第 3 节中已述，整个标定过程是通过更新传感器的各个参数进行迭代计算的(选取迭代次数为N＝200)。在迭代的过程中，传感器的各个参数均收敛且最终趋于稳定，证明了本方法是可行的。以 1 号传感器为例，传感器在三个方向轴上的灵敏度系数最终收敛稳定于 kx＝4.855，ky＝5.096，kz＝4.776。灵敏度系数的收敛性如图12 所示。

同样以 1 号传感器为例，传感器位置的值最终收敛稳定于 x＝0.1933，y＝0.0419，z＝—0.1033(单位：m)，位置校正迭代的收敛性如图13 所示。

1 号传感器 x 轴方向参数最终收敛稳定于 M1＝(0.960，0.009，—0.079)，x 轴方向系数校正迭代的收敛性如图10 所示；y 轴方向参数最终收敛稳定于 M2＝(—0.055，0.946，0.050)，y 轴方向系数校正迭代的收敛性如图11 所示；z 轴方向参数最终收敛稳定于 M3＝(—0.034，—0.024，0.984)，z 轴方向系数校正迭代的收敛性如图14～16 所示。

即得，1 号传感器的方向矩阵为：

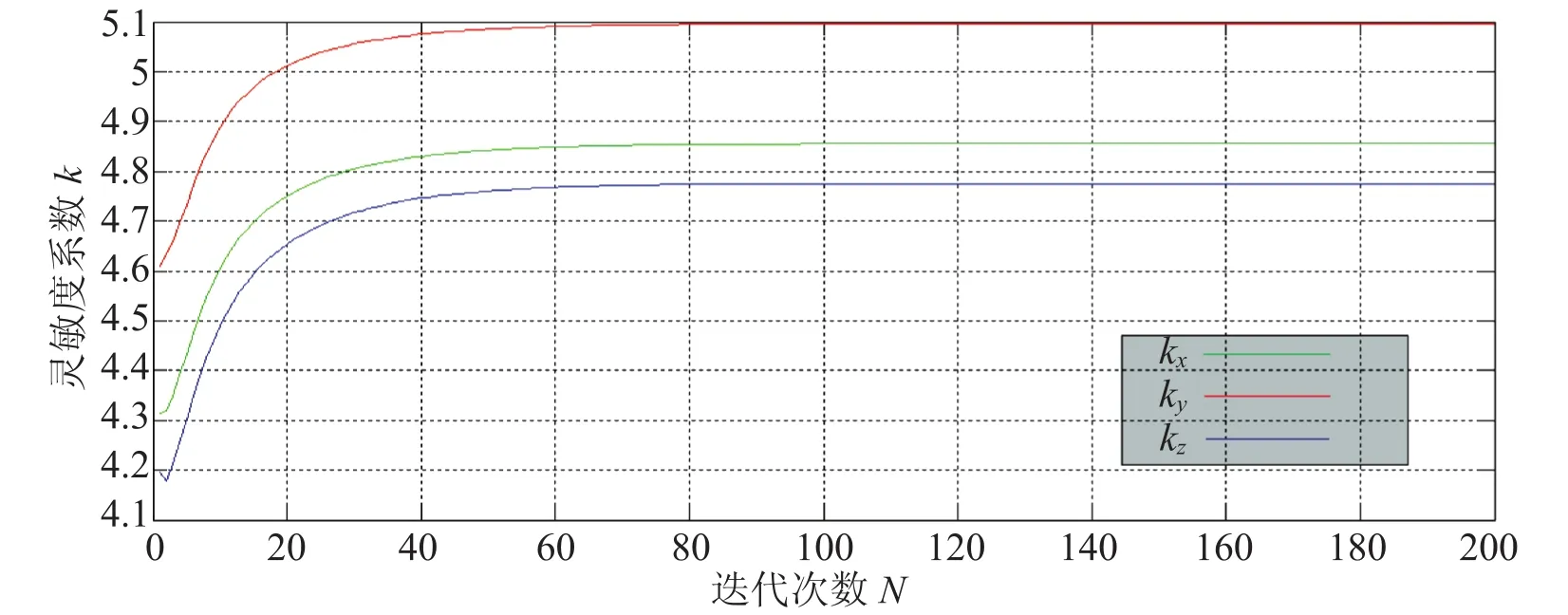
图12 传感器灵敏度收敛性Fig.12. Convergence of magnetic sensor sensitivity

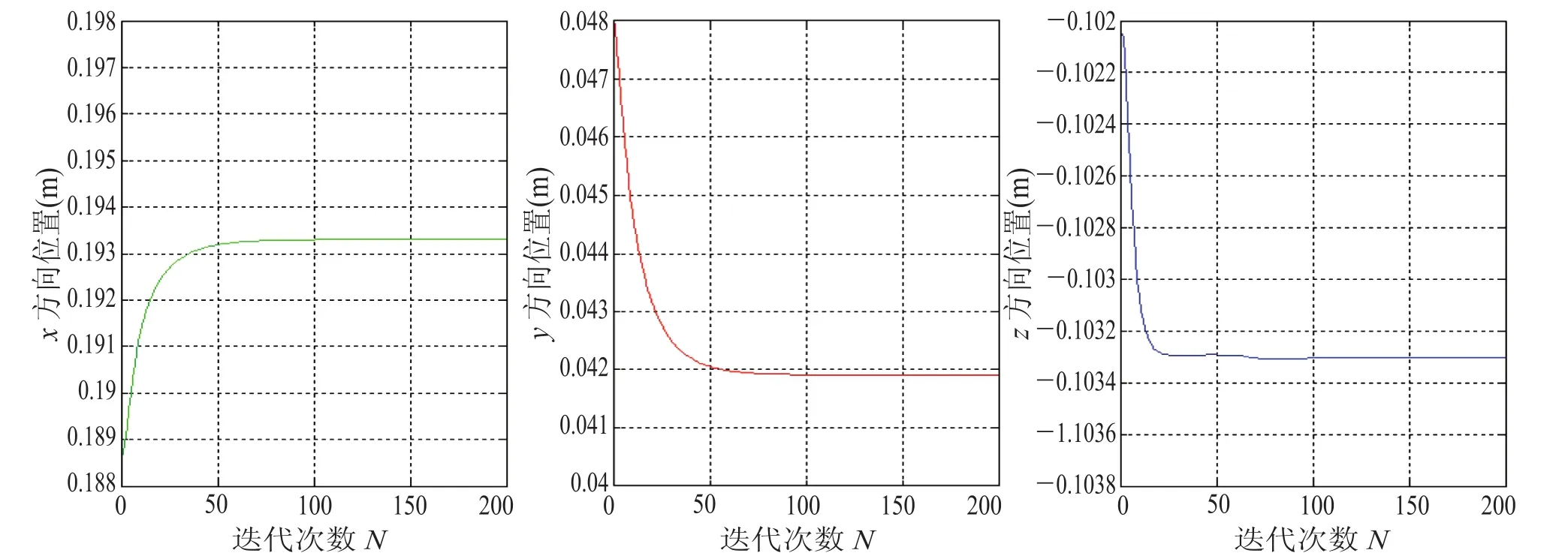
图13 传感器位置收敛性Fig.13. Convergence of magnetic sensor position

图14 传感器 x 轴方向系数收敛性Fig.14. Convergence of magnetic sensor orientation in the x direction

图16 传感器 z 轴方向系数收敛性Fig.16. Convergence of magnetic sensor orientation in the z direction

同样方法可标定 2 至 32 号传感器的位置，方向以及灵敏度系数。

4.2 传感器标定前后定位精度的比较

传感器标定前，采取定点定向的方式在 33个点对永磁体进行定位测试，系统定位误差如图17 所示。x 轴方向平均定位误差 4.14 mm，y 轴方向平均定位误差 3.31 mm，z 轴方向平均定位误差 4.29 mm。

传感器标定后，取同样的 33 个点再次对永磁体进行定位测试，系统定位误差如图18 所示。x 轴方向平均定位误差 1.76 mm，y 轴方向平均定位误差 1.42 mm，z 轴方向平均定位误差1.52 mm。

传感器标定前，系统对永磁体定向误差如图19所示。x 轴方向平均定向误差 2.99°，y 轴方向平均定向误差 2.73°，z 轴方向平均定向误差 3.18°。

传感器标定后，系统对永磁体定向误差如图20 所示。x 轴方向平均定向误差 1.74°，y 轴方向平均定向误差 1.48°，z 轴方向平均定向误差1.89°。

图17 传感器标定前定位误差Fig.17. Positioning error before calibration

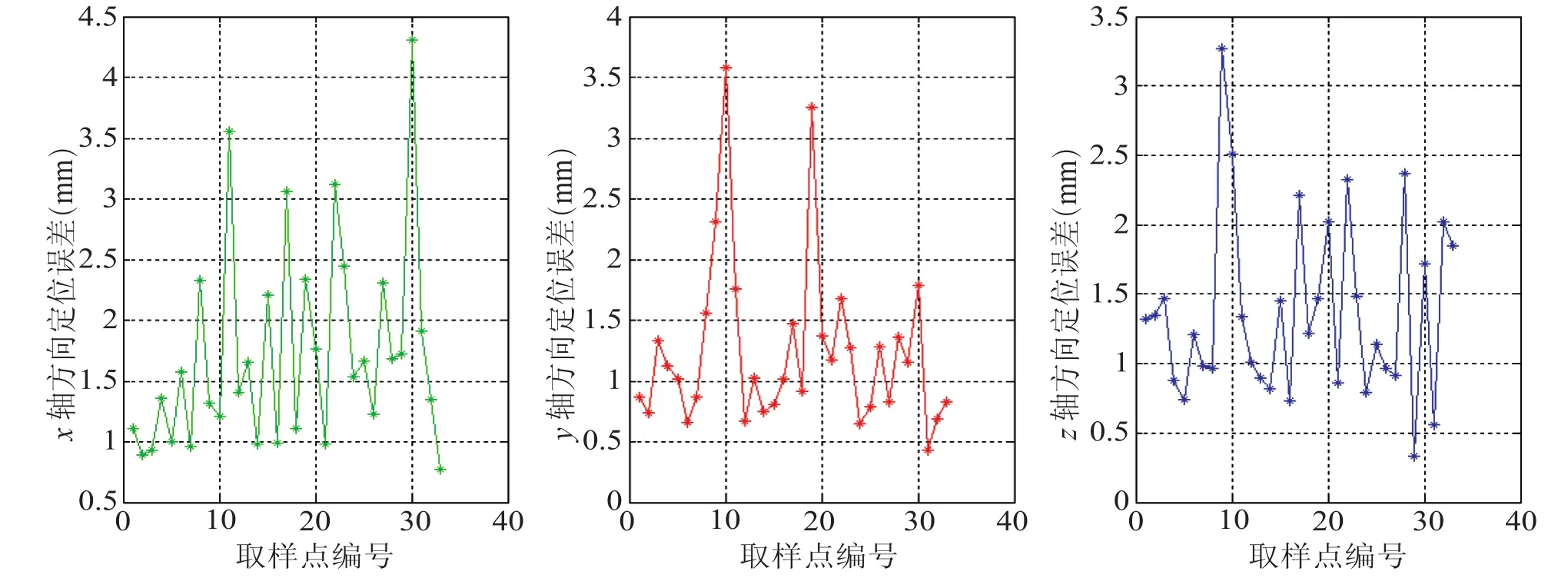
图18 传感器标定后定位误差Fig.18. Positioning error after calibration

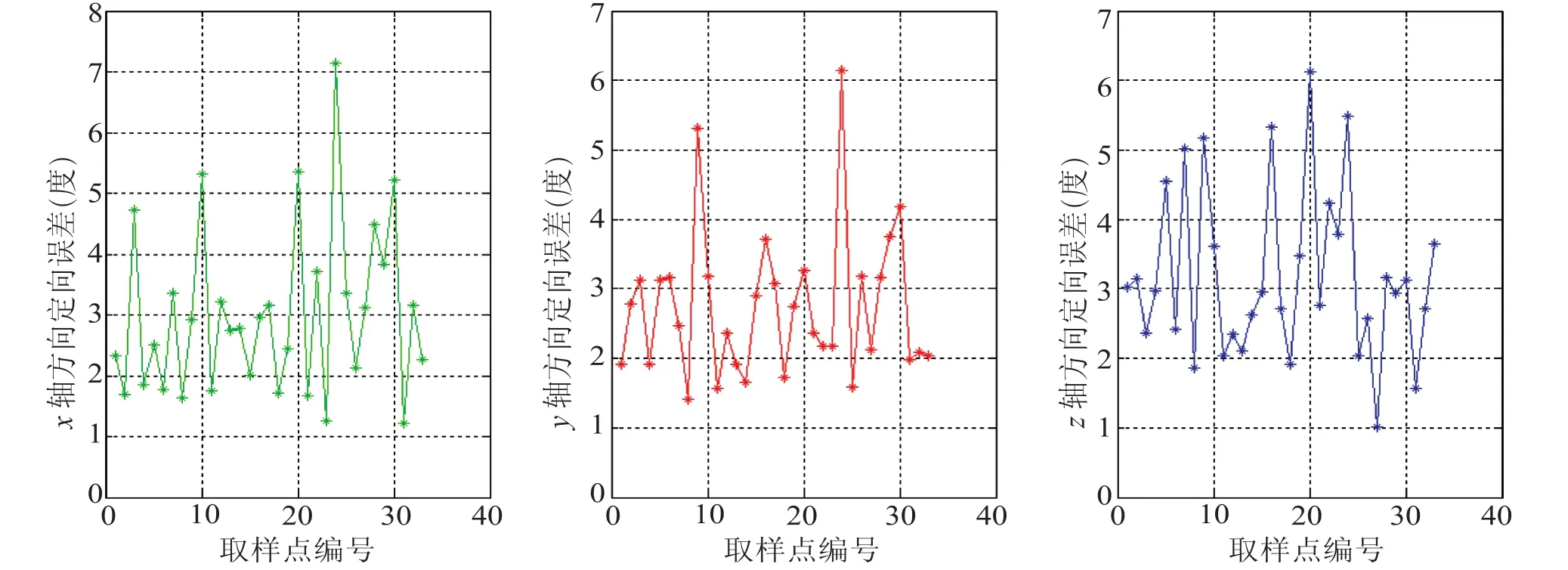
图19 传感器标定前定向误差Fig.19. Directional error before calibration

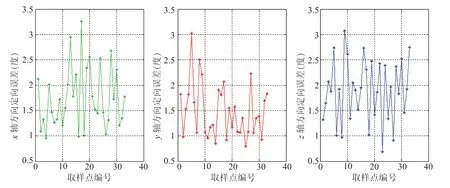
图20 传感器标定后定向误差Fig.20. Directional error after calibration

5 结 论

本文针对人体内运动磁目标跟踪定位的传感器标定问题，提出了一种最优化方法，建立误差函数，通过更新参数、迭代计算的方法对磁传感器的位置、方向、灵敏度系数进行标定计算。编写 MATLAB 程序进行计算，最终得到磁传感器阵列各个传感器的精确位置、方向和灵敏度系数。

实验证明，本文提出的标定方法可行、设计的硬件电路合理，可使系统的定位误差从 4 mm左右降至 1 mm 左右、定向误差从 3°左右降至1°左右。对磁传感器阵列的各个参数进行精确标定，可以大大降低系统对永磁体的定位定向误差，提高磁定位系统的精度和稳定性。

[1] Iddan G, Meron G, Glukhovsky A, et al. Wireless capsule endoscopy [J]. Nature, 2000, 405: 417-417. doi: 10.1038/35013140.

[2] Hu C. Localization and orientation system for robotic wireless capsule endoscope [D]. University of Alberta, 2006.

[3] 何文辉, 颜国正, 郭旭东. 基于磁阻传感器的消化道诊查胶囊的位置检测 [J]. 仪器仪表学报, 2006, 27(10): 1187-1190.

[4] Li JQ. Calculating the magnetic fi eld of a magnetic dipole by biot-savart’s law [J]. Physics and Engineering, 2004, 14(4): 14-15.

[5] Hu C, Meng MQH, Mandal M. A linear algorithm for tracing magnet’s position and orientation by using three-axis magnetic sensors [J]. IEEE Transactions on Magnetics, 2007, 43(12): 4096-4101.

[6] 胡超, 宋霜, 阳万安, 等. 胶囊内窥镜位置方向磁场定位技术的研究 [J]. 集成技术, 2012, 1(1): 105-113.

[7] Hu C, Li M, Song S, et al. A cubic 3-axis magnetic sensor array for wirelessly tracking magnet position and orientation [J]. IEEE Sensors Journal, 2010, 10(5): 903-913.

[8] Yang WA, Hu C, Li M, et al. A new tracking system for three magnetic objectives [J]. IEEE Transactions on Magnetics, 2010, 46(12): 4023-4029.

A Calibration Method for the Magnetic Target Tracking System

HU Chao1REN Yupeng1,2WANG Wenhu3SONG Shuang4FENG Zhongqing1,2WANG Yonghui1,2YUAN Xiaoying1,2
1( School of Information Science and Engineering, Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, China )
2( Taiyuan University of Science and Technology, Taiyuan 030024, China )
3( Faculty of Information Science and Engineering, Ningbo University, Ningbo 315211, China )
4( Department of Biomedical Engineering, National University of Singapore, Singapore 119077, Singapore )

The magnetic sensor array Honeywell HMC1043 was used to collect the magnetic information of the permanent magnet. Because the precision of the system is directly affected by sensor parameters including the position, the direction and the sensitivity coefficient of the sensor array, the accurate calibration of the magnetic sensors was indispensable to obtain the accurate sensor parameters of the sensor array in the magnetic tracking system. A method of objective error function and optimization calculation for the problem of magnetic sensors calibration was proposed in this paper. The error function was minimized through updated parameters and iterative calculation. Then the accuratelocation, direction and sensitivity coef fi cient of the sensors array were obtained. This method was applied to the actual sensor system. In MATLAB environment, the position, the direction and the sensitivity coef fi cient of the sensor array were determined through calculation and the magnetic information of the permanent magnet was collected by the computer to realize calibration. By this method, the accuracy of the system localization was improved signi fi cantly, which therefore veri fi ed the feasibility and rationality of the algorithm.

permanent magnet localization; magnetic sensor array; position and direction; sensitivity coef fi cient

TP 212.9

A

2014-08-01

国家自然科学基金(61273332)

胡超，特聘教授，博士生导师，研究方向为自动化、智能信息处理和机器人控制；任宇鹏(通讯作者)，硕士，研究方向为自动化、嵌入式控制系统与应用，E-mail：riencype@163.com；王文虎，硕士，研究方向为物联网终端协议和软件开发；宋霜，博士后，研究方向为生物医学工程、计算机应用和机器人控制；冯忠晴，硕士，研究方向为自动化、嵌入式控制系统与应用；王永辉，硕士，研究方向为自动化和智能信息处理；袁小英，硕士，研究方向为智能信息与图形图像信息处理。