基于 MEKF 的直流无刷电机磁极位置与转速检测技术

屈稳太王 郎王 领,2

1(浙江大学宁波理工学院 宁波 315100)

2(浙江大学控制科学与工程系 杭州 310058)

基于 MEKF 的直流无刷电机磁极位置与转速检测技术

屈稳太1王 郎1王 领1,2

1(浙江大学宁波理工学院 宁波 315100)

2(浙江大学控制科学与工程系 杭州 310058)

传统的扩展卡尔曼滤波器(Extended Kalman Filter，EKF)用于无刷直流电机状态辨识时，观测数据容易出现残差，辨识结果偏差大，位置及转速存在耦合，导致辨识系统鲁棒性弱。文章基于离散的直流无刷电机(Brushless DC Moter，BLDCM)数学模型和 M-估计方法，构建了改进的扩展卡尔曼滤波算法(MEKF)。首先，基于 BLDCM 的工作原理，建立了独立于 EKF 的 BLDCM 换相离散模型；其次，通过修正系统观测矩阵，对转速与位置的强耦合关系进行解耦，实现了 EKF 分离变量辨识；最后，基于去耦合后的时序模型设计出独立于 EKF 的转子位置检测模块，无需深度滤波就可实现转子的精确定位。实验仿真结果表明，文章方法能够有效抑制卡尔曼滤波器的粗差扰动，提高了系统抵抗初始值不确定性的干扰和系统鲁棒性。

无刷直流电机；扩展卡尔曼滤波；无传感器检测；M-估计

1 引 言

直流无刷电机(Brushless DC Motor，BLDCM)由于其结构简单、维护简便、易于调速的优点，在工业生产中得到广泛应用。然而传统的 BLDCM 需要通过位置传感器获取转子磁极位置信号进行换相，使其抗扰性能下降、应用环境受到限制、制造成本增加[1-3]。

扩展卡尔曼滤波器(Extended Kalman Filter，EKF)作为卡尔曼滤波在非线性系统上的拓展，通过对过程信息的在线积累与更新，可实现BLDCM 非线性系统的次优状态辨识[4,5]。传统 EKF 将转速与位置作为待辨识状态，由于这两者之间具有强耦合关系以及观测状态存在残差[5]，导致系统鲁棒性降低；而且耦合关联误差、初始状态设定误差都在一定程度上影响了辨识精度[6,7]。

本文基于电机动态模型提出了一种基于 M-估计[8]的 EKF 辨识算法以及独立的换相模块。文中对系统观测矩阵进行 M-估计修正，抑制系统残差噪声扰动；同时基于状态空间模型，将位置与转速的强耦合关系进行动态解耦，消除耦合误差对关联状态辨识的影响，实现转速及位置独立辨识；解耦算法对 EKF 系统状态更新及观测矩阵进行重构，实现转速基于历史信息的定权重自辨识及扰动抑制；换相模块基于线反电动势在线计算，设计出端点可测变量与换相信号的直接映射关系，从而实现独立于转速的浅度滤波换相。

2 BLDCM 模型与传统 EKF 算法

BLDCM 在静态 abc 坐标系下的数学模型如下：

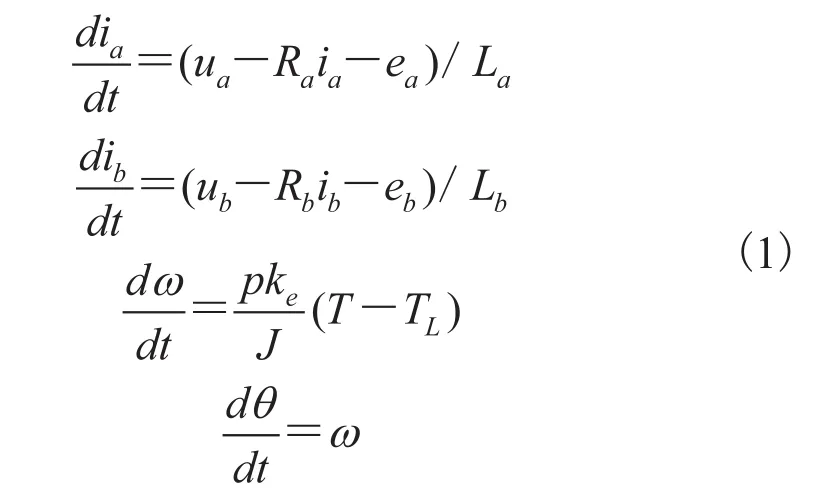
其中，ia、ib和 ua、ub分别为 BLDCM 定子的A、B 相电流和相电压；Ra、Rb和 La、Lb分别为 A、B 相电阻和电感，且 Ra＝Rb＝R，La＝Lb＝L；ω 为转子转速；θ 为转子位置；p 为极对数；J 为转动惯量；ke为反电动势系数；ea、eb为相应的反电动势。

根据电机数学模型，列出系统状态方程：

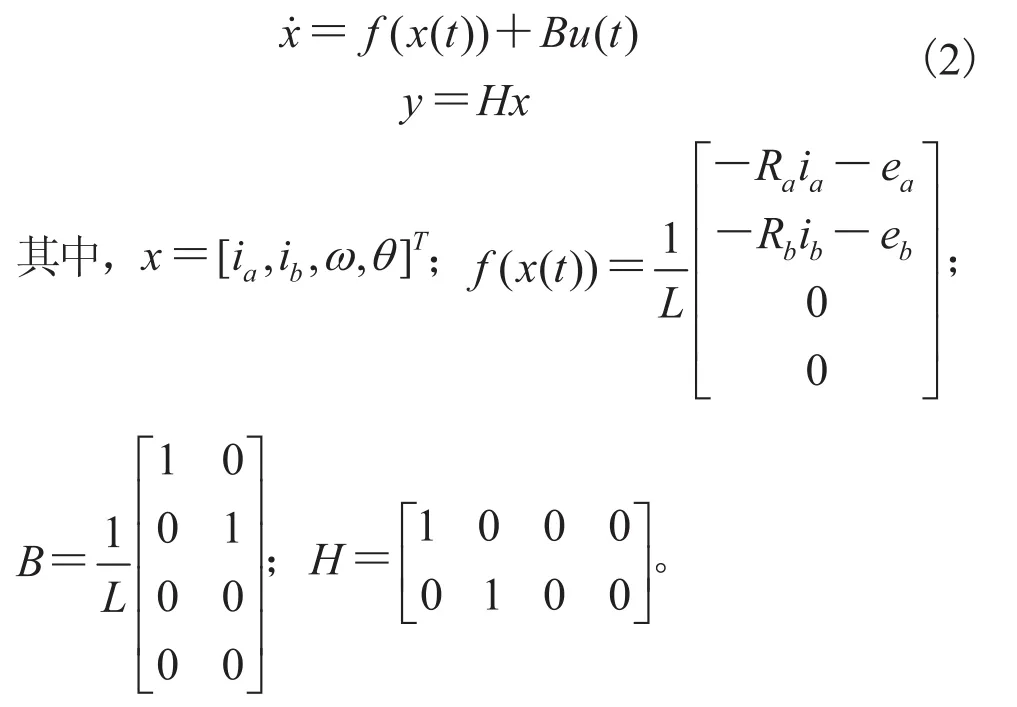
BLDCM 反电动势波形为 120°电角度的梯形波， a、b、c 依次相差 120°电角度，如图1所示。

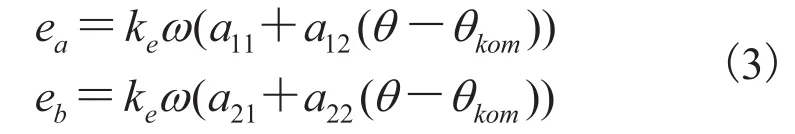
其中，a11～a22分配值见表1；fi x 为取整函数。

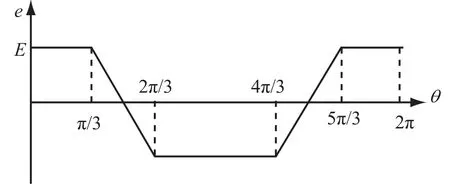
图1 反电动势波形Fig.1. Wave of EMF

根据相反电动势与转子位置的定量数学关系，可以得到 f(x) 的雅可比矩阵如下：

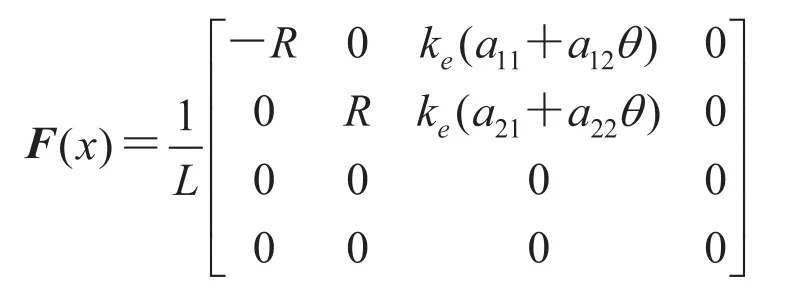
系统离散状态方程即可由下式表示出：

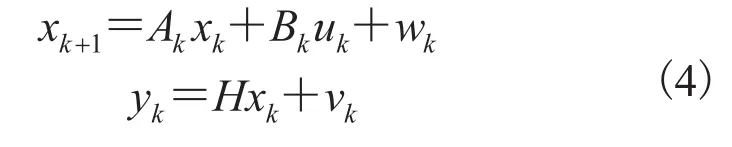
根据(4)式离散模型，可构造扩展的卡尔曼滤波算法

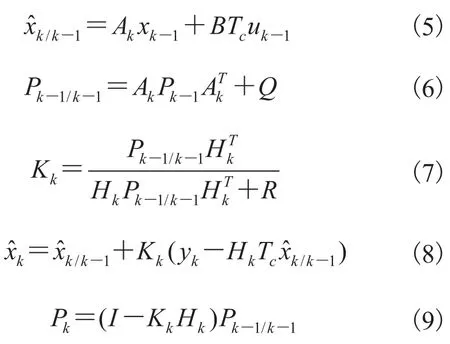
3 基于 EKF 的 BLDCM 改进型辨识算法

由(1)式可知，假定 ia检测值与理论值保持一致，如果位置出现辨识偏差，则同时刻关联的速度误差

表1 a11～a22分配值Table1. Assigned value of a11～a22

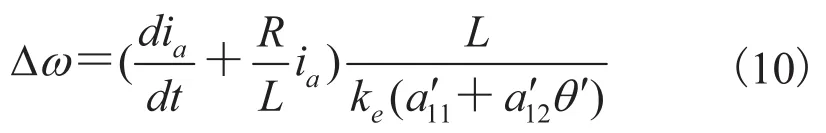
3.1 独立换相模块

由图1 可以得出，相反电动势 ea是以 2π 为周期的偶函数，其傅里叶级数展开为：

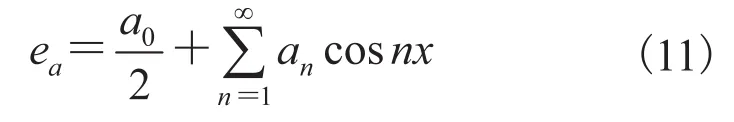
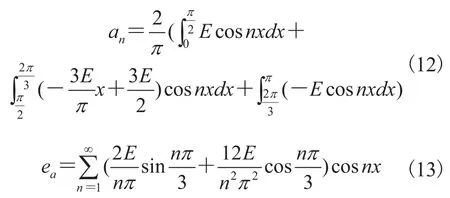
ea、eb、ec相位差依次为 2π/3，则线电动势

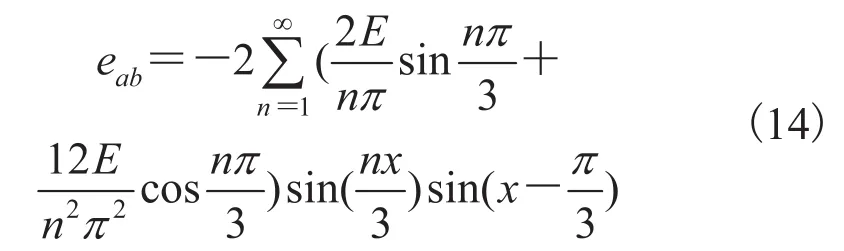
由(14)式，单周期内 eab的过零点为 π/3、4π/3。同理可得 ebc的过零点为 0、π；eca的过零点为 2π/3、5π/3。过零点与系统原始换相点完全一致。

根据(1)式即可构造出与 EKF 辨识系统弱关联的电机换相模块，通过线反电动势过零点的检测，实现无相移的零点定位，从而避免传统的深度滤波器检测所带来的相位偏移[11]。

3.2 EKF 速度检测算法

位置信息由独立换相模块进行检测，速度信号通过改进的 EKF 算法进行单变量辨识与检测。带位置传感器 BLDCM 系统中，三个位置传感器输出表征转子位置的六个状态的脉冲信号，每个位置传感器在经过系统 t 时间换相之后，相邻换相时间间隔与逐渐趋于相等，即

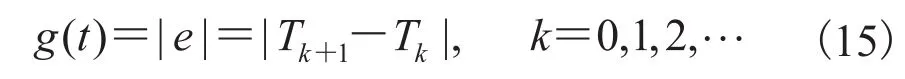
其中，g(t)为总体趋于 0 的非光滑函数。此时

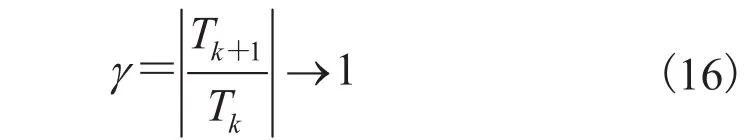
在保证辨识稳定的情况下，可进一步进行如下假设：

读写分离 有的老师在读写结合过程中为了读写结合而结合，“写”与“读”之间的关系显得很生硬，存在阅读与写作分离现象，不能把阅读、积累、实践、写作有机地紧密结合起来，甚至破坏了阅读情绪，提不起学生的表达欲望。

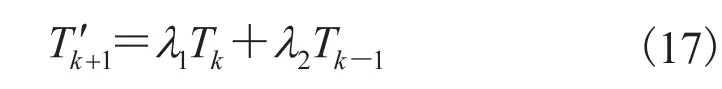
即通过记录前两次的换相间隔时间来进行当前换相间隔时间的预估。其中，、为两次换相间隔时间的比重权值，且有；为时刻理论换相间隔时间；Tk为 k 时刻实际记录的换相间隔时间。

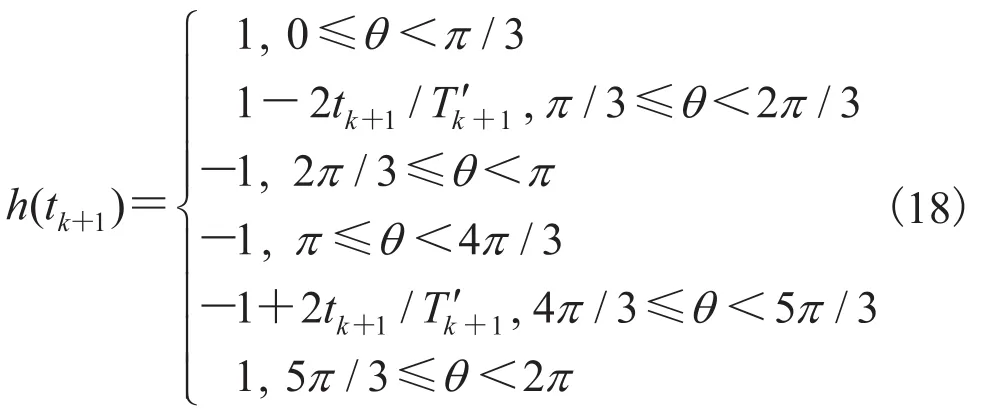
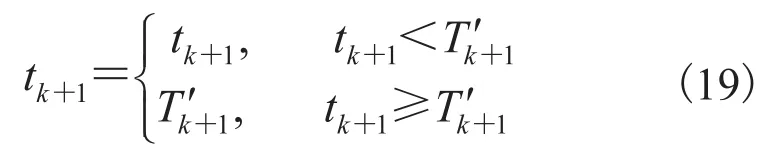
3.3 基于 M-估计的新息修正算法

在传统的扩展卡尔曼模型中，通过电流、电压反馈信息进行的线性递推，系统扰动直接通过观测值反馈到辨识模型中，系统观测矩阵将无法真实反映实际观测量。此时，预测时间序列出现新息残差：

其中，Ek为测量干扰分量。此时残差新息序列为

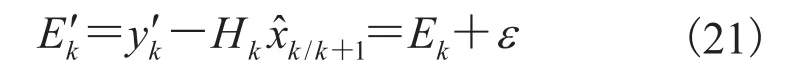
系统扰动破坏了新息序列的零均值高斯分布统计信息的条件。为保证系统辨识精度，需对残差进行补偿或修正。

M-估计为基于最小二乘法的抗差估计[8]，令根据其准则函数：

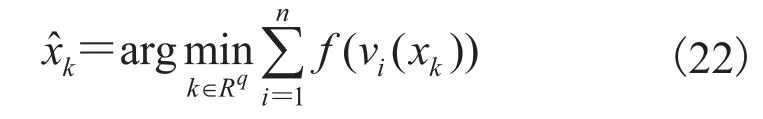
其中，n 为观测向量维数；f(x)为影响函数。对被估状态求导，并代入观测方程

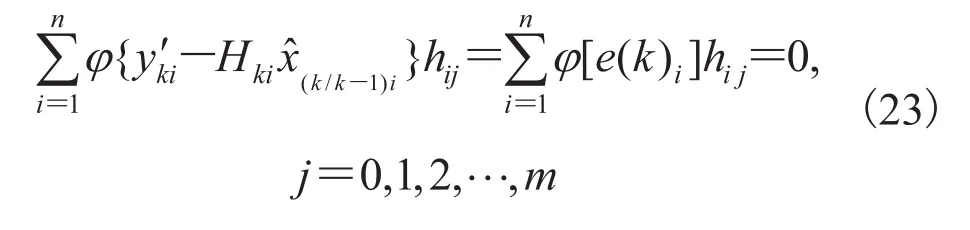
其中，hij为观测矩阵相应变量；m 为待辨识状态维。权函数直接决定系统影响函数，反映了系统的鲁棒性，由 Huber 法[9]进行权函数选取，其中尺度参数 v 可由实际调试或通过自适应算法求出[10]。根据 M-估计器，

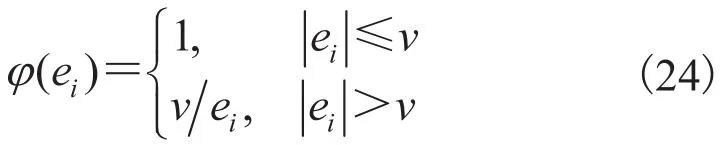
将方程(23)、(24)代入(22)并结合方程组(1)，通过对换相时间的预估，即可实现独立于位置 θ 的 EKF 单变量的辨识。

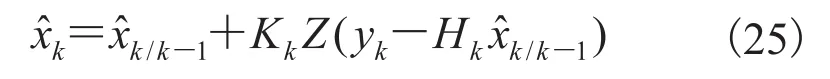
4 系统仿真及实验结果

采用 Matlab/Simulink 软件对提出的辨识系统进行仿真，仿真结构图如图2 所示。电机磁极对数 p＝4，其模型参数为：定子电阻 R＝0.2 Ω，自感 L＝0.0025 H，转动惯量 J＝0.089 kg·m2，反电动势常数 ke＝0.15 V／rpm，永磁磁链＝0.083 Wb。

4.1 仿真结果

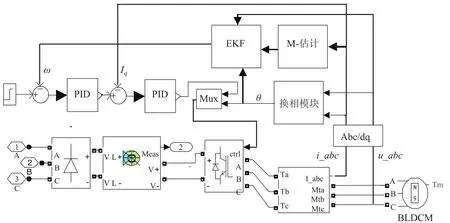
图2 无传感器 BLDCM 仿真图Fig.2. Simulation structure of sensorless BLDCM

图3 为换相模块仿真结果。由于电机内部换相以及微分环节的存在，在线反电动势中出现较大峰值脉动，导致换相脉冲中存在一些尖峰干扰，如图3(a)所示；加入一阶滤波环节，选取适当滤波参数，能够实现反电动势零点处的平滑过渡，换相脉冲如图3(b)所示。

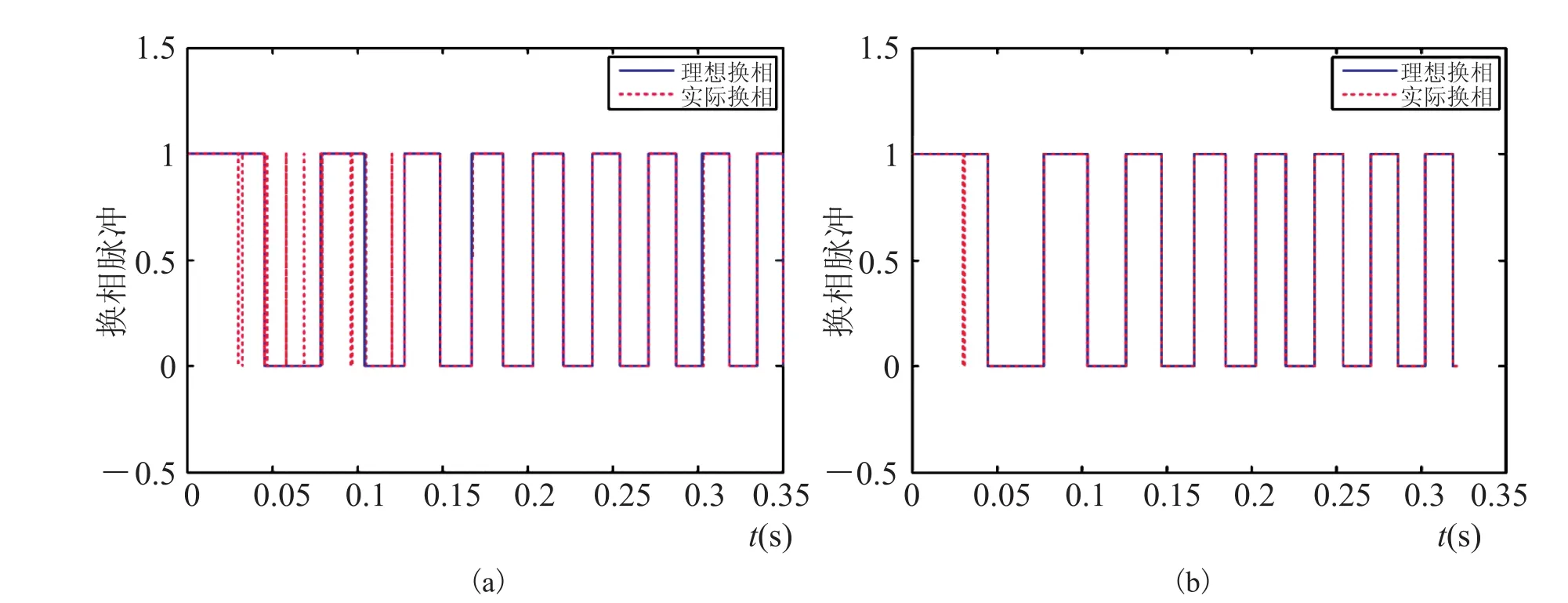
图3 系统换相脉冲对比Fig.3. Comparison of commutation pulse of system

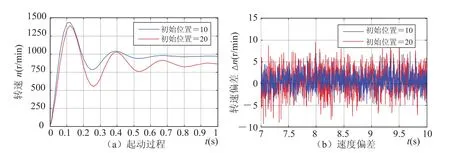
图4 传统 EKF 算法的起动过程与速度偏差Fig.4. Start process and errors of speed under conventional EKF

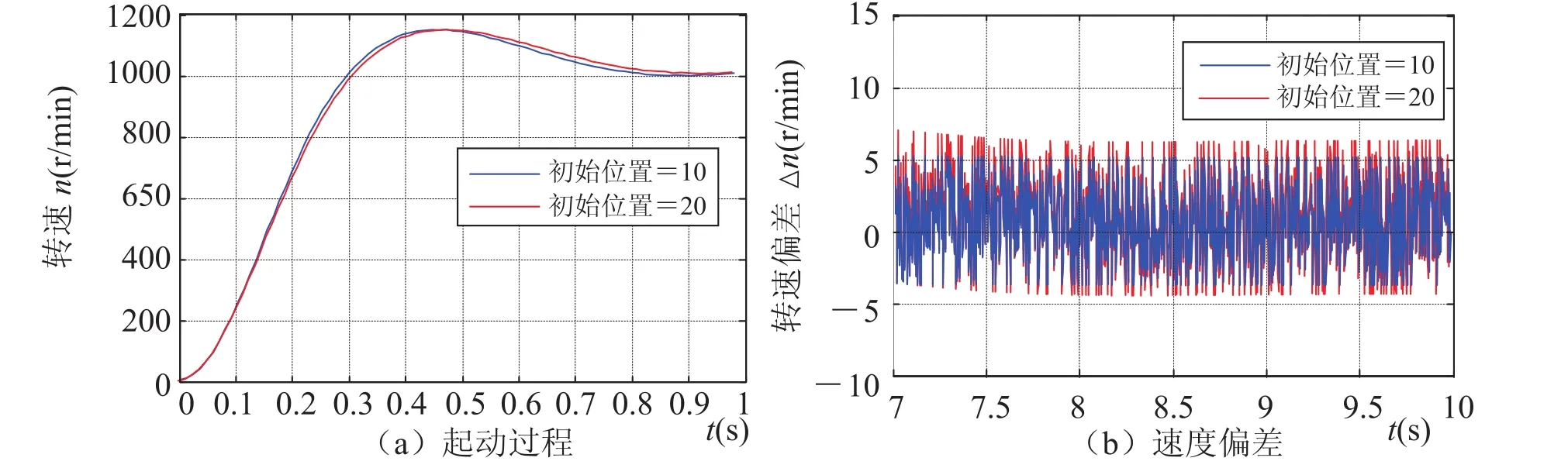
图5 MEKF 算法的起动过程与速度偏差Fig.5. Start process and errors of speed under the MEKF

图4、图5 分别为传统 EKF 算法与 MEKF算法下的速度跟踪与速度误差仿真结果。其中，图4(a)为传统 EKF 算法时无位置传感器的电机转子在不同初始位置时的启动状态，速度给定为1000 r/min，初始位置分别设为 10°及 20°，由图可见系统转速对转子初始位置较为敏感，适应能力弱；图4(b)所示为传统 EKF 算法时无位置传感器电机速度与有位置传感器电机速度绝对差值 |△n|，速度给定为 1000 r/min，由图可见其差值在 [0, 20] 之间。

图5(a)为 MEKF 算法时无位置传感器的电机转子在不同初始位置时的启动过程，速度给定为 1200 r/min，初始位置分别设为 10°及 20°，由图可见系统转速对转子初始位置具有较强的适应能力；图5(b)所示为无位置传感器电机速度与有位置传感器电机速度绝对差值 |△n|，速度给定为 1200 r/min，由图可见其差值在 [0, 6] 之间。

由仿真结果可见，MEKF 的速度跟踪特性比传统的 EKF 鲁棒性好，速度误差小。

4.2 实验结果

实验系统结构与仿真系统结构图相同，如图2 所示，采用 TMS320F2812 作为核心控制芯片，搭建实验系统，系统参数修改为：电机磁极对数 p＝2，定子绕组电阻 R＝2.875 Ω，自感 L＝0.0085 H，转动惯量 J＝0.0008 kg·m2，反电动势常数 ke＝0.35 V／rpm，永磁磁链＝0.175 Wb。图6(a)所示为在观测值上强加尖峰干扰脉冲，图6(b)为相应的系统速度偏差响应。由图6可见，具有 M-估计的 EKF 速度偏差明显要小于传统的 EKF 速度偏差。图7(a)所示为在观测值上强加带限白噪声干扰，图7(b)为相应的系统速度偏差响应，其结果与图6 有类似结果。由此可见，对于传统的 EKF 辨识系统，其前提条件是假设观测信息具有特定的统计特性，而当观测值强加干扰时，其统计信息被破坏，辨识就会出现较大偏移，系统抗扰动能力较弱；而对观测矩阵进行 M-估计修正，系统对瞬时扰动及持续噪声扰动均具较强抑制能力，同时系统也具有较强的鲁棒性。

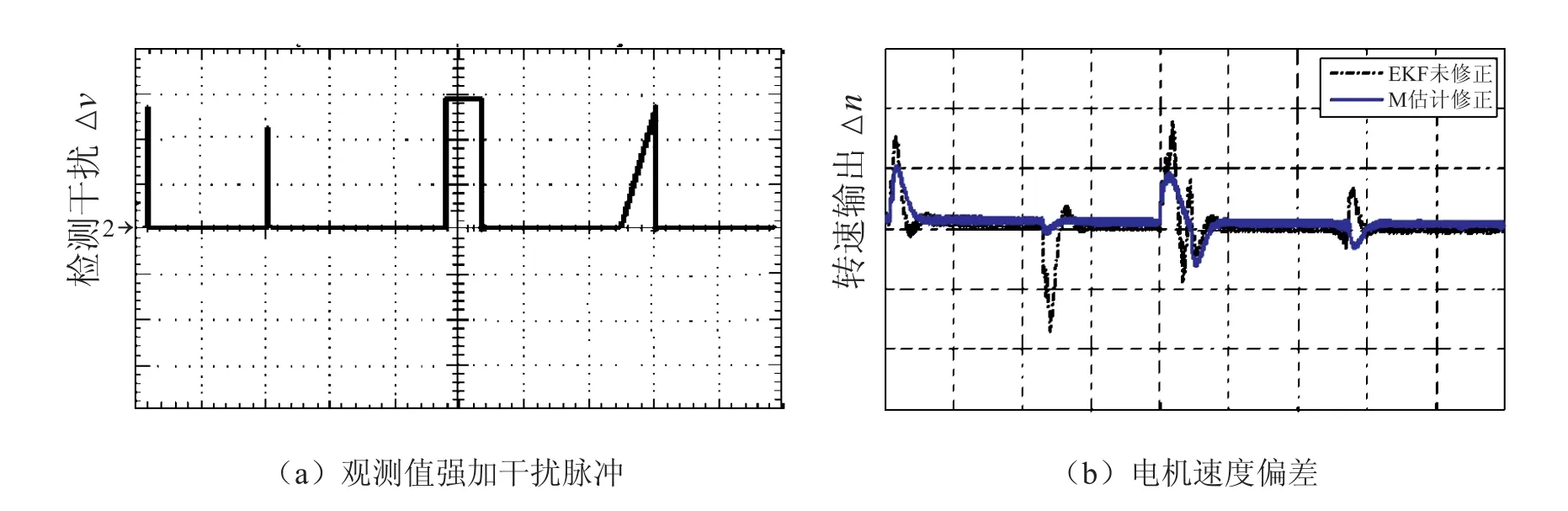
图6 尖峰干扰下，速度误差实验结果Fig.6. Experimental results of speed errors under the spike impulse interfere

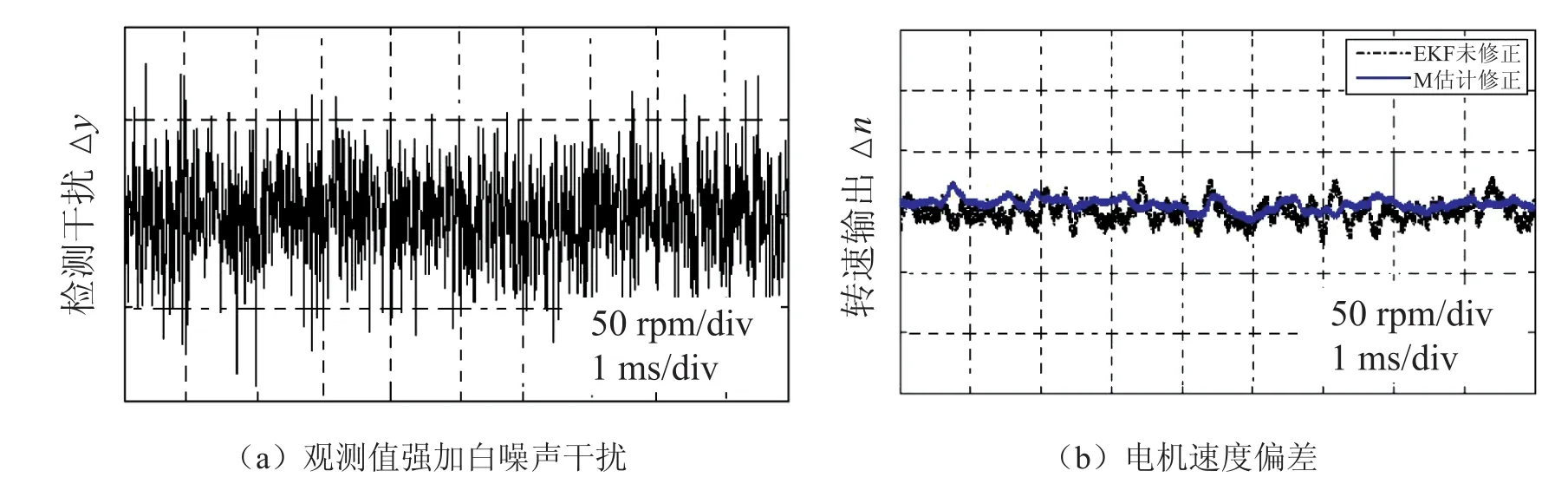
图7 白噪声扰动下，速度偏差实验结果Fig.7. Experimental results of speed errors under the white noise interfere

5 结 论

为了实现无刷直流电机无位置传感器的控制，本文提出了一种基于 M-估计修正的 MEKF的速度和位置辨识算法。该算法对 EKF 系统观测矩阵进行 M-估计修正，实现残差抑制；对辨识系统的速度和位置进行了解耦，实现了 EKF速度和位置的独立辨识；基于解耦后的电机时序模型，设计出独立于 EKF 的电机换相模块。

研究结果表明，MEKF 辨识算法能够实现对速度和位置的分离辨识，消除观测数据残差，增强了系统鲁棒性；提出的独立换相模块减少了初始位置不确定性，降低了传统滤波相移所带来的辨识偏差，从而有效减小了系统的速度偏差和跟踪误差，提高了系统抗扰动性及辨识精度。

[1] Matsui N, Shigyo M. Brushless DC motor control without position and speed sensor [J]. IEEE Transactions on Industry Applications, 1992, 28(1): 120-127.

[2] Acarnley PP, Watson JF. Review of positionsensorless operation of brushless permanent-magnet machines [J]. IEEE Transactions on Industrial Electronics, 2006, 53(2): 352-362.

[3] Gamazo-Real JC, Vázquez-Sanchez E, Gomez-Gil J. Position and speed control of brushless DC motors using sensorless techniques and application trends [J]. Sensors, 2010, 10(7): 6901-6947.

[4] Terzic B, Jadric M. Design and implementation of the extended Kalman fi lter for the speed and rotor position estimation of brushless DC motor [J]. IEEE Transactions on Industrial Electronics, 2001, 48(6): 1065-1073.

[5] Chan SC, Zhang ZG, Tse KW. A new robust Kalman filter algorithm under outliers and system uncertainties [C] // Proceedings of IEEE International Symposium on Circuits and Systems, 2005, 5: 4317-4320.

[6] 徐璟, 孙旭东, 刘丛伟. 用 EKF 估计无刷直流电动机转子位置和转速 [J]. 清华大学学报(自然科学版), 2004, 44(7): 905-908.

[7] 李自成. 无刷直流电机无位置传感器控制关键技术研究 [D]. 武汉: 华中科技大学, 2010.

[8] Ma SG, Kosorok MR. Adaptive penalized M-estimation with current status data [J]. Annals of the Institute of Statistical Mathematics, 2006, 58(3): 511-526.

[9] Hermey D, Watson GA. Fitting data with errors in all variables using the Huber M-estimator [J]. SIAM Journal on Scientific Computing, 1999, 20(4): 1276-1298.

[10] 胡玉锁, 陈宗海. 一种基于鲁棒估计的自适应的图像平滑方法 [J]. 中国科学技术大学学报, 2006, 36(2): 153-157.

[11] 崔丽娜, 夏超英, 赵玲. 基于“线电压”的 BLDCM 无位置传感器控制 [J]. 微特电机, 2011, 39(2): 50-52.

Detection Technology of Rotor Position and Speed of BLDCM Based on MEKF

QU Wentai1WANG Lang1WANG Ling1,2
1( Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, China )
2(Department of Control Science and Engineering, Zhejiang University, Hangzhou 310058, China )

The traditional Extended Kalman Filter (EKF) will lead to large errors of estimation data and robustness weakening of the identi fi cation system when applied to brushless DC motor (BLDCM) to estimate rotor position and speed simultaneously. In this paper, based on the discrete mathematical model of BLDCM and M-estimation, an improved EKF (MEKF) was proposed. Firstly, based on the commutation principle of the BLDCM operation and EKF model, a separate commutation model was built up, which was independent to the EKF. Secondly, in order to identify the rotor speed and position with more precision and to enhance the robustness of system, the observation matrix was modi fi ed by M-estimation, and a decoupling technology of speed and position was adopted in the system correspondingly. Thirdly, based on the decoupled time series model of the motor, a rotor position detection model was designed out, so that a precision rotor position can be realized in practice without deep fi ltration which will lead to great lagging. The experiment and simulationresults show that this method can effectively abate the errors disturbance of the EKF, and it also signi fi cantly enhances the anti-interference of the initial value and robustness.

BLDCM; EKF; sensorless detection; M-estimation

TM 351

A

2014-07-14

宁波市自然科学基金(2011A610135)；宁波市重大专项(2012B10050)

屈稳太(通讯作者)，博士，教授，研究方向为电机控制、电能变换及智能控制，E-mail：wentaiqu@zju.edu.cn；王郎，博士，硕士生导师，研究方向为信号处理；王领，硕士研究生，研究方向为电机控制和嵌入式系统。