基于两级模糊识别的桥型方案优选模型

邹惠鑫，郑建荣*，王淑妹

（福建农林大学交通与土木工程学院，福建福州350002）

基于两级模糊识别的桥型方案优选模型

邹惠鑫，郑建荣*，王淑妹

（福建农林大学交通与土木工程学院，福建福州350002）

根据桥型设计方案资料，对包含定性指标的桥型方案进行客观评价。以马洋大桥设计方案为研究案例，根据两级模糊识别原理，提出定性指标相对隶属度确定方法，采用多目标最大距离法计算指标权重，建立基于两级模糊识别的桥型方案优选模型。优选结果为矮塔斜拉桥方案，符合客观实际。

桥型方案；模糊识别；权向量；相对隶属度；多目标最大距离法

0 引言

桥梁方案比选涉及造价、施工难度等多项因素，影响因素间的关系复杂，对定性因素通常是通过设计人员判断给出评价，缺乏客观性。采用模糊识别可将定性因素进行量化，便于科学地对桥型进行优选。本文依托两级模糊识别模型［1］及相关模糊数学理论，采用最大距离法确定指标权重，建立新的模糊优选模型，并通过实例验证了该模型。

1 桥型方案比选模型

1.1 方案集的指标特征矩阵

依据影响桥梁结构形式主要因素选定因素集C=（c1，c2，…，cm），根据桥型方案设计条件确定方案集V=（v1，v2，…，vn），其中ci（i=1，2，…，m）表示第i个影响因素，vj（j=1，2，…，n）表示第j个桥梁比选方案。则方案集V的指标特征值矩阵为

其中xij表示对于方案j因素i的特征值。

1.2 定性指标优越性排序

就定性指标ci对方案进行优越性对比，建立优越性的定性排序特征值矩阵

其中e按下式进行取值

其中ielk=1-ielk，k=1，2，…，n；l=1，2，…，n。

根据相关理论，对所得矩阵进行优越性排序一致性检验，并对矩阵进行调整，使其满足优越性排序一致性特征值矩阵的要求。对调整后矩阵各行和数进行从大到小的排列，给出方案集关于优越性排序。

1.3 确定相对隶属度矩阵［1-2］

1.3.1 定量指标相对隶属度根据文献［2］，对

于越大越优型特征值的相对隶属度公式为

对于越小越优型特征值的相对隶属度公式为

1.3.2 定性指标相对隶属度结合方案vj就定性指标ci定性排序，根据文献［2］，建立方案集V就定性指标ci对优越性的有序二元比较矩阵

满足条件式中ialk为就指标ci，方案vl对vk就优越性进行二元比较时，方案vl对vk的优越性定量标度；iakl为就指标ci，方案vk对vl就优越性进行二元比较时，方案vk对vl的优越性定量标度；排序下标l=1，2，…，n；k=1，2，…，n；序号根据矩阵各行和数从大到小的次序排列。

方案vi就指标ci相对隶属度公式为

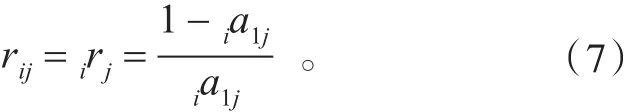
为了便于给出优越性定量标度，文献［1］建立了符合我国语言习惯的语气算子、定量标度及相对隶属度之间的对应关系，见表1。

表1 语气算子、定量标度及相对隶属度关系表Tab.1 Relationship among mood operator，quantitative scale and relative membership grade

1.4 多目标最大距离法计算指标权重

多目标最大距离法的基本思想是：依据客观统计的数据，寻找一个权重向量，使各方案与理想方案的加权距离最大，从而将这些方案更明显地区分开来［3］。

根据上述方法计算各个因素相对隶属度，建立目标相对优的相对隶属度矩阵

由模糊原理及文献［4］可知，可将矩阵R转置作为规范化后的决策矩阵

为确定各指标权重W=（w1，w2，…，wm），建立多目标最优化模型

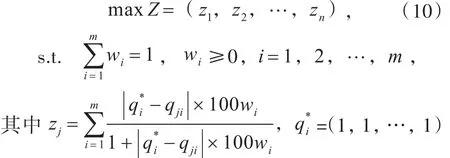
为指标的“理想值”。zj的含义为各方案vj=（qj1w1，qj2w2，…，qjmwm）同理想方案v*=（1·w1，1·w2，…，1·wm）之间的距离，即可作为对该方案的一种评价。

上述多目标最优化模型采用线性综合方法，将它转化为单目标最优化模型，即

根据上述模型，调用MATLAB最优化工具箱中的fmincon函数解出W=（w1，w2，…，wm）。

1.5 计算各方案评价值

将软件运行结果W=（w1，w2，…，wm）代入，求得各个方案的综合评价值并进行从大到小排序。

从模型建立的意义可知，所得出的综合评价值越大，说明方案偏离理想值越大；反之，综合评价值越小，说明方案越接近理想值。因此，可得出最优方案为综合评价值最小的方案。

2 桥型方案比较实例

本文以永泰县马洋大桥桥型方案选择为例。马洋大桥是衔接大樟溪两岸的重要部分，亦是永泰城市景观建设的华重一笔。桥型方案的选择除了满足桥梁使用功能和桥下通航要求外，桥梁应具备结构安全实用、造价经济、外形美观，同时应尽量采用新结构、新工艺，施工技术难度适中，力求造型新颖，做到与周围环境相协调。

2.1 建立特征矩阵

影响桥型选择的因素很多，本文主要选择5个因素，构成因素集C=（工期c1，施工难度c2，维护成本c3，景观效果c4，造价c5）［5］。其中c1和c5是两个结构性（定量）因素，c2、c3、c4是3个非结构性（定性）因素。

依据桥梁设计标准、地面线形式、地质水文等情况以及桥梁选型原则，构成方案集V=（三塔扇形索矮塔斜拉桥v1，中承式钢管系杆拱桥v2，上承式葵花形拱桥v3，无背索斜拉桥v4）［6-10］。

根据类似桥型方案指标及相关工程经验建立桥型方案比较表（特征矩阵），如表2所示。

2.2 定性指标优越性排序

就定性指标c2对方案进行优越性定性对比，

表2 桥型方案比较表Tab.2 Comparison of bridge type schemes

建立优越性定性排序特征值矩阵经检验，矩阵满足优越性排序一致性特征值矩阵的要求。对矩阵各行和数进行从大到小的排列，得方案优越性排序依次为2、4、1、3。依照上述方法对定性指标c3、c4进行排序。

2.3 确定相对隶属度矩阵

2.3.1 定量指标相对隶属度c1、c5属于越小越优型指标，应用（5）式进行计算，本文仅列出1r的计算过程。

则1r=（1.000，0.923，1.000，0.889）。

2.3.2 定性指标相对隶属度经认真考虑，认为对指标c2，优越性排序为1的方案v3，与排序为2的方案v1相比为“略为”优越；与排序为3的方案v4相比为“极其”优越，与排序为4的方案v2相比为“明显”优越。查表1，即可得

2r=（0.667，0.111，1.000，0.429）。

类似地，可以确定指标c3、c4的相对隶属度。得到相对隶属度矩阵为

2.4 指标权重计算

将矩阵R进行转置得到决策矩阵根据（11）式，调用fmincon函数，解出

W=（0.218，0.148，0.134，0.153，0.347）。

2.5 计算各方案评价值

z1=0.114，z2=0.295，

z3=0.120，z4=0.287，由此得zmin=z1=0.114，即最优方案为方案一。

2.6 优选结果分析

从优选结果可以看出，方案一略优于方案三，明显优于其他方案。该方案施工难度、维护成本、造价适中，工期短，能和周边环境相协调，景观效果好。因此方案一作为优选方案较为合理。

3 结语

1）采用基于两级模糊识别桥型优选模型，通过对影响桥梁桥型选择的不同指标采用不同方法确定相对隶属度，客观地给出桥型方案评价值，降低人为判断的影响。

2）根据两级模糊识别模型的建立原理，采用多目标最大距离法，建立多目标最优化模型，通过MATLAB软件计算指标权重，简化传统计算权重步骤，提高了计算精度。

（References）

［1］陈守煜.工程模糊集理论与应用［M］.北京：国防工业出版社，1998.

［2］徐飙.二元论方法在桥梁方案比选中的应用［J］.黑龙江交通科技，2007（1）：68-69，71.

［3］刘新建，张瑞凤.多目标决策中一种确定权重的方法［J］.山西师范大学学报：自然科学版，2002，16（3）：20-22.

［4］杨虹，万忠伦.价值工程中确定功能权重的方法［J］.西华大学学报：自然科学版，2005，24（2）：77-79.

［5］张海龙.模糊数学在桥梁方案确定中的应用［J］.桥梁建设，1993（3）：72-76.

［6］中交公路规划设计院.JTG D60-2004公路桥涵设计通用规范［S］.北京：人民交通出版社，2004.

［7］中交公路规划设计院.JTG D62-2004公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京：人民交通出版社，2004.

［8］陈宝春.桥梁工程［M］.北京：人民交通出版社，2009.

［9］金立新，郭慧乾.多塔斜拉桥发展综述［J］.公路，2010（7）：24-29.

［10］吴巨军，赵林强.系杆葵拱桥设计研究［J］.公路，2007（9）：12-15.

（责任编辑：曾婷）

Optimization of Bridge Type Schemes Model Based on Two-Extreme Fuzzy Recognition

ZOU Huixin，ZHENG Jianrong*，WANG Shumei
（College of Traffic and Civil Engineering，Fujian Agriculture and Forestry University，Fuzhou 350002，Fujian，China）

Based on information of bridge type design scheme，objectively evaluates the bridge type scheme including qualitative index．Taking the design schemes of Mayang New Bridge as an re⁃search object，propose the method for qualitative index to solve relative membership grade．Multi-objective maximum distance method is introduced into the calculation of the index weight．Based on two-extreme fuzzy recognition theory，optimization of bridge type schemes model is estab⁃lished．The short tower cable-stayed bridge is the optimized outcome which is consistent with the objective reality．

bridge type scheme；fuzzy recognition；weight vector;relative membership grade；multi-objective maximum distance method

U442.54

A

1673-0143（2014）02-0041-04

2014-02-20

邹惠鑫（1986—），男，硕士生，研究方向：桥梁结构。

*通信作者：郑建荣（1964—），男，副教授，研究方向：桥梁结构。E-mail：364167349@qq.com