孤子方程的达布变换及其精确解

王振辉，李世金

（河南理工大学数学与信息科学学院，河南焦作454003）

且b、c满足方程组

孤子方程的达布变换及其精确解

王振辉，李世金

（河南理工大学数学与信息科学学院，河南焦作454003）

总结比对了多组孤子方程如KdV方程、MKdV方程、KP方程等的达布变换，并借助其平凡解，讨论了若干孤子方程的精确解。

孤子方程；达布变换；精确解

达布变换最先是由19世纪末法国数学家Darboux在研究线性Sturm-Liouville问题时提出的。其基本思路是利用非线性偏微分方程的一个解及其对应的特征方程的解，用代数算法微分运算来得出非线性偏微分方程的新解和特征方程的新解，再利用达布变换的迭代性质，得到非线性偏微分方程的无数个新解。

1986年，中国科学院院士谷超豪等人将Dar⁃boux变换用矩阵形式表述，说明达布变换实际上就是带谱参数的规范变换。可以利用纯代数算法来构造达布变换，并可以将达布变换推广到两个和多个空间变量的情形，极大地推广了达布变换的应用范围。目前达布变换已经成为孤子理论中的一个重要研究热点［1-2］。

1 多组孤子方程的达布变换

1.1 KdV方程的达布变换KdV方程是关于φ的线性方程组

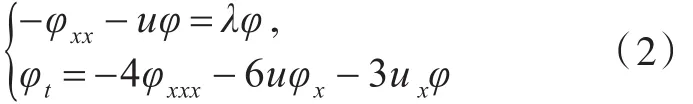
的可积条件，这里u和φ是关于x和t的函数。

设u(x)和φ(x，λ)是满足方程（2）的两个函数，对任意给定的常数λ0，令f(x)=φ(x，λ0)，即f是方程（1）当λ=λ0时的一个解。

经过计算可知，由

所定义的函数u′满足与方程（1）具有相同形式的方程方程组（3）即为KdV方程的达布变换。

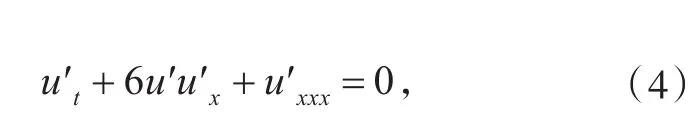
1.2 MKdV方程的达布变换MKdV方程

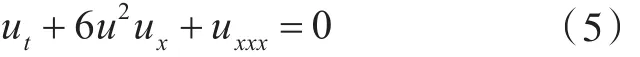
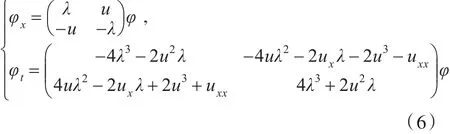
是关于二元列向量φ的线性方程组的可积条件，这里u和φ是关于x和t的函数。已知φ=

是方程组（6）的解，令ψ=φ1+iφ2，则ψ满足方程

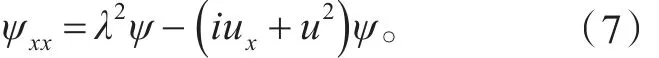
设u是MKdV方程的一个解，记方程（7）当λ=λ0时的解f=f1+i f2，则可以推导出MKdV方程的另一个解变换（8）即可以作为MKdV方程的达布变换。

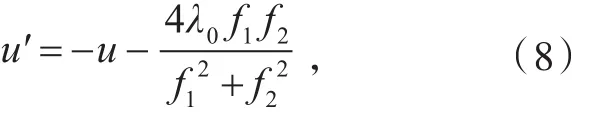
1.3 KP方程的达布变换

KP方程反映了二维水波的运动，最早是由Kadomtsev和Petviashvili提出的。

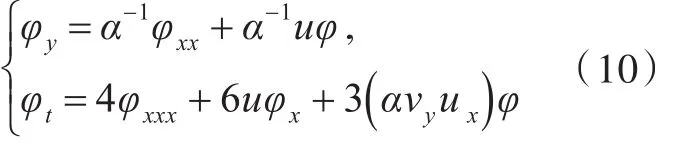
KP方程是关于φ的线性方程组的可积条件，其中u和φ是关于x、y和t的函数。

取h为方程（9）的一个解，设φ是方程组（10）的任一解，定义则φ′满足方程组

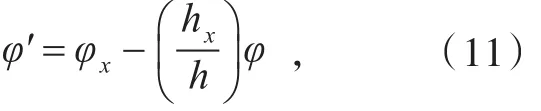
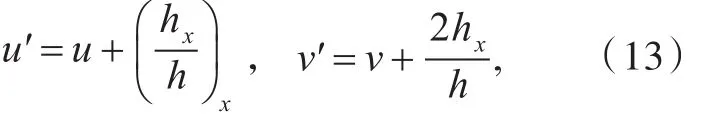
其中，方程组（12）与（10）形式相同，仅仅是(u，φ)换成了(u′，φ′)，变换（13）即可以作为KP方程的达布变换。

1.4 Broer-Kaup（BK）系统问题的达布变换［3-5］

BK系统问题

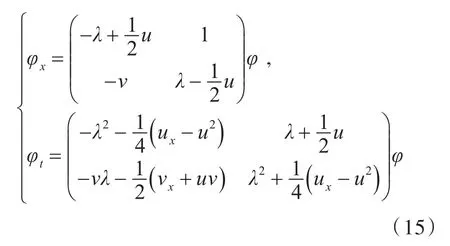
是关于二元列向量φ的线性方程组的可积条件，这里的u和φ是关于x和t的函数。引入规范变换φˉ=Tφ，满足方程

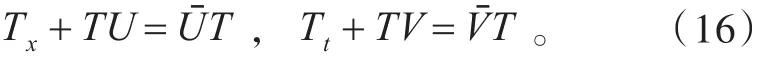
（15）的两个基本解，令

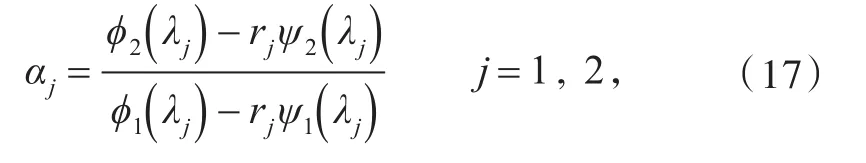
经过计算推导，可以给出达布变换

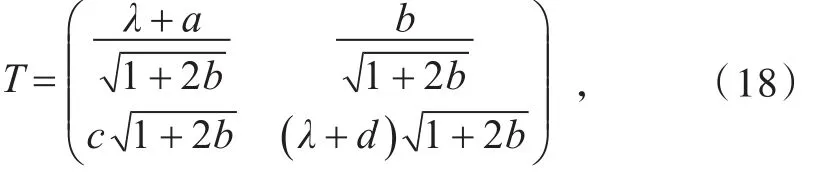
其中，a、b、c、d满足方程组

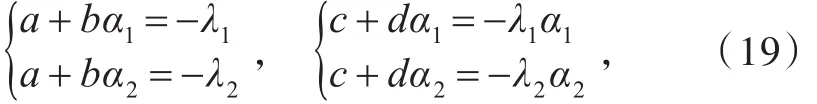
且b、c满足方程组

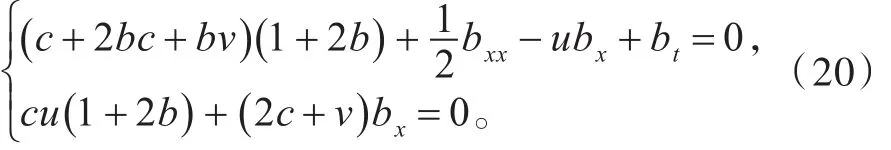
由式（16）可得

方程组（21）即为BK系统问题的达布变换。

1.5 Boussinesq方程的达布变换

Boussinesq方程

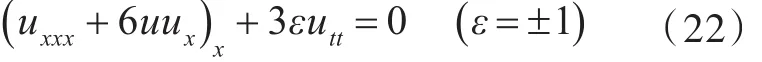
是关于φ的线性方程组的可积条件，其中，

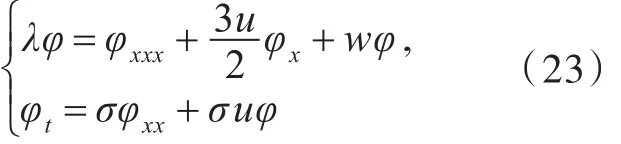
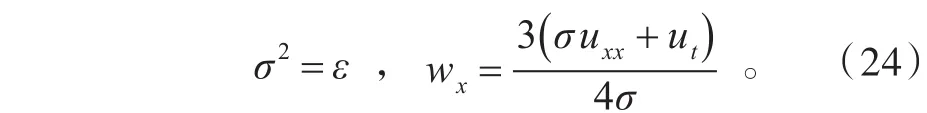
经过计算推导可知，Boussinesq方程的达布变换是

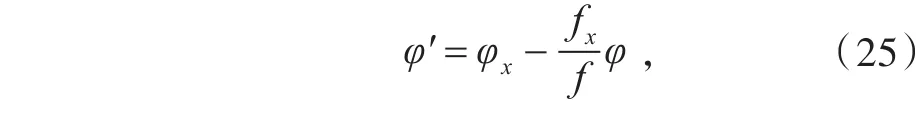
其中，f是方程组（23）当λ=λ0时的一个解。

2 两组孤子方程的精确解

下面分别从MKdV方程和BK系统问题的一个平凡解出发，利用变换（8）和（21），讨论运用达布变换方法如何求孤子方程的精确解。

2.1 MKdV方程的精确解

取MKdV方程（5）的平凡解u=0作为出发点，取方程组（6）的基本解为

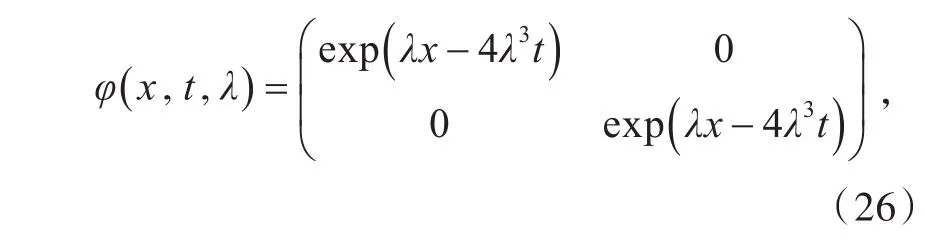
对常数λ1≠0及μ1=exp() 2α1，有

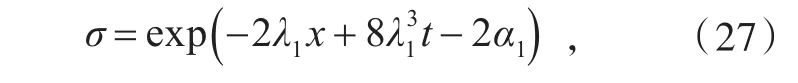
从而

其中，

利用达布变换（8）可以给出MKdV方程的单孤子解

相应于u′，方程组（6）的新解为

如果将u′作为新的出发点，则可以利用φ′作新的达布阵，以得到MKdV方程的一系列的新解，推导过程与上面类似，这里直接给出MKdV方程的双孤子解

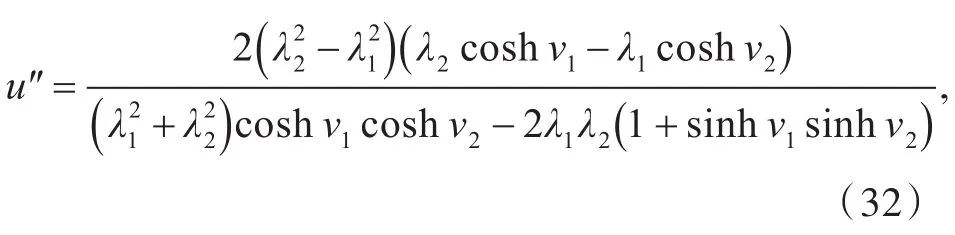
其中vi=2λix-8λ3it+2αi(i=1，2)，λ2≠0为常数。

2.2 BK系统问题的精确解

取BK系统问题的平凡解u=0，v=1，代入

方程组（15），求得基本解

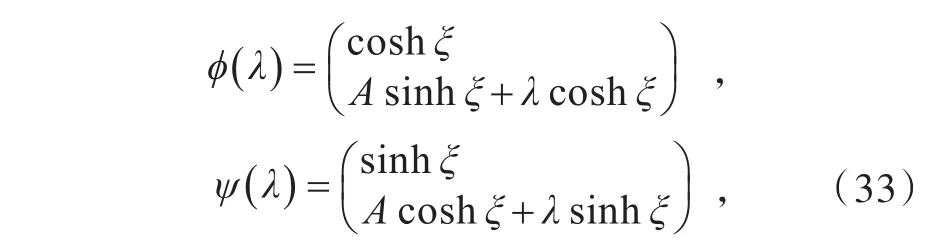
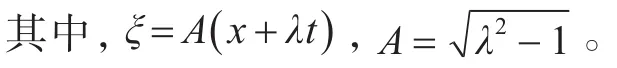
将（33）式代入（17）式，经过计算可得

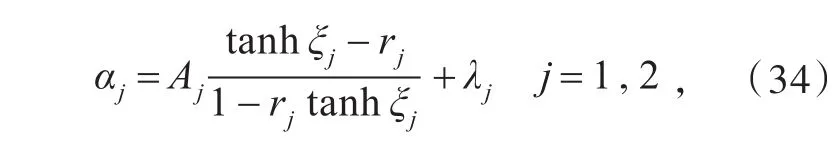
其中，ξi=Ai() x+λit，Ai=为任意常数。

利用达布变换（21）得到BK系统问题的新解为

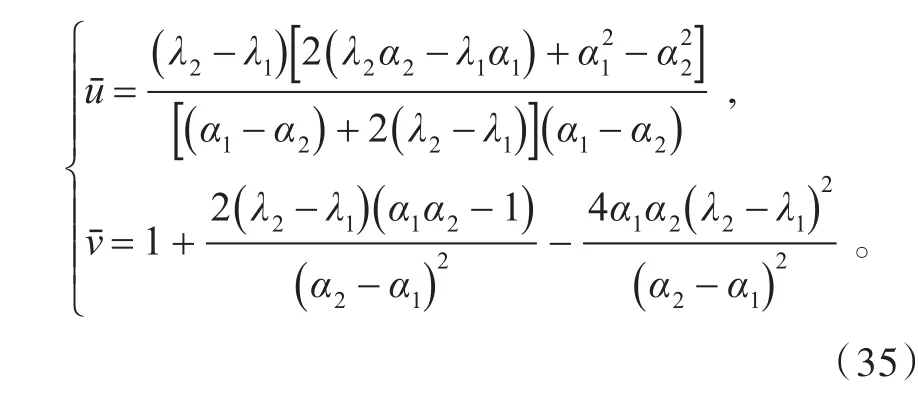
3 结语

在求解孤子方程的诸多方法中，达布变换方法是一种自然而美妙的方法，它从平凡解出发可以得到孤子方程的精确解。达布变换方法的优点是只须作一次完全可积的线性方程组的求解，然后便可利用代数运算得到非线性孤子方程的新解，它的关键点是寻找一种保持相应的Lax对不变的规范变换。

（References）

［1］谷超豪，胡和生，周子翔.孤子理论中的达布变换及其几何应用［M］.上海：上海科学技术出版社，1999：1-12.

［2］LI Y S，MA W X，ZHANG J E．Darboux transforma⁃tions of classical boussinesq system and its new solu⁃tions［J］.Phys Lett A，2000，275（2）：60-66.

［3］周振江，李志斌.Broer-Kaup系统的达布变换和新的精确解［J］.物理学报，2003，52（2）：262-266.

［4］刘萍，张金顺.Broer-Kaup系统的达布变换及其奇孤子解［J］.西南师范大学学报：自然科学版，2006，3l（5）：31-36.

［5］黄坤，陈友军.Broer-Kaup系统3类达布变换间的关系及其精确解［J］.郑州大学学报：理学版，2012，44（3）：38-41.

（责任编辑：强士端）

Darboux Transformation and Explicit Solutions of Soliton Equations

WANG Zhenhui，LI Shijin
（School of Mathematics and Information Science，Henan Polytechnic University，Jiaozuo 454003，Henan，China）

Summaries and contrasts Darboux transformation of several group soliton equations such as KdV equation，MKdV equation，KP equations and so on，and with the assistance of the trivial so⁃lution，discusses the exlicit solutions of some Soliton equations.

soliton equation；Darboux transformation；exlicit solution

O175.29

A

1673-0143（2014）02-0034-03

2014-03-06

国家自然科学基金资助项目（11226102）；河南理工大学青年基金项目（Q2012-30A）

王振辉（1982—），男，讲师，硕士，研究方向：孤子理论。