地质风险评价中的不确定性分析
盛秀杰,金之钧,徐忠美,蒋 瀚
(1.中国石油化工股份有限公司 石油勘探开发研究院,北京 100083;2.中国地质大学(北京) 信息工程学院,北京 100083)
地质风险评价中的不确定性分析
盛秀杰1,金之钧1,徐忠美1,蒋 瀚2
(1.中国石油化工股份有限公司 石油勘探开发研究院,北京 100083;2.中国地质大学(北京) 信息工程学院,北京 100083)
地质风险概率法被广泛应用于油气资源评价中的地质风险评价。由于很难直接定义每一地质评价因子的评价(“打分”)概率模型,专家给出的都是每一评价因子的确定性评价值(“点估计”)—— 单一的、确定性评价结果并不能够很好地反映目标区域复杂地质情况的多种可能性,不可避免地出现含油气有无的高估或低估的情况。结合油气资源一体化评价软件(PetroV)的开发经验,从如何更客观地去描述地质评价因子的不确定性入手,阐述如何采用多种不确定性分析技术,更好地融合、体现专家经验以及客观表达地下复杂地质情况,从而提高地质风险概率法的不确定性表达能力:(1)通过自信度转换数学模型体现专家主观认知的不确定性;(2)将专家的定性认知进行合理的知识规则化转换,充分量化地质模型的不确定性;(3)基于地质风险概率法数学模型,利用蒙氏模拟计算符合概率分布特征的地质风险评价结果;(4)据地质风险不确定性评价结果,可获取目标区域地质风险评价的多分位评价值,为后续的勘探决策给出尽可能全面的决策方案。
自信度转换;模糊逻辑;蒙氏模拟;不确定性评价;地质风险分析;油气资源评价
基于最新勘探资料进行地质风险评价,是回答目标区域油气资源有无的主要研究活动。定量地质风险评价主要包括地质风险分析和不确定性评价两部分内容[1-3]。地质风险分析,也称地质风险概率法,是在给出缺一不可的成藏地质条件的主观评价值(也称“打分值”)基础上,通过连乘来计算目标区域的地质风险确定性评价结果[4];而不确定性评价是基于成藏地质条件多种可能性的定量描述,来获取符合某种概率分布的地质风险不确定性评价结果。一旦确定了评价目标以及关键地质评价因子,合理的地质风险评价结果来自于准确了解地质不确定因素并尽可能使其充分呈现出来。业内学者也一直致力于如何很好地刻画油气成藏过程的不确定性,进而获取合理的地质风险评价结果[5-8]。尽管如此,对地下认知的不确定性表达仍然是地质风险评价面临的主要瓶颈。为了合理估算不确定条件下的某些地质条件的评价值范围,本文结合PetroV软件的时间开发经验[9],提出了一种全新的定量评价思路(图1):强调利用多种不确定性定量分析技术,分层次刻画从主观推测到客观预测过程中的不确定性,最终给出尽可能全面的不确定性地质风险评价结果。不确定性分析技术主要包括:(1) 通过自信度转换体现专家主观认知的不确定性;(2) 将专家的定性认知进行合理的知识规则化转换,使得对地质评价参数的分析从基于单一可能性的“纯粹”定量分析过渡到基于多种可能性的“模糊”定量分析,尽可能使不确定性降到最低;(3)基于地质风险概率法,利用蒙氏模拟获取多因子综合地质风险评价结果的不确定性表达,也就是符合概率分布特征的地质风险不确定性评价结果。
1 基于自信度转换的不确定性分析
地质风险概率法强调油气成藏过程所受的控制因素很多,生油层、储集层、盖层、圈闭、运移、保存及相互之间的配置关系是其主要影响因素(式1中的Pi);上述成藏地质条件是决定目标区域是否具有油气藏的系列独立事件,意味着缺一则该区域都不能形成油气藏。因此,目标区域是否存在油气的可能性,就可以用独立事件同时发生的概率乘积来表示(式1)。其中,单项成藏地质条件(式1、2中的Pi)存在发生的概率,又可进一步依赖于其子项成藏地质因素(式2中的Pij)的好与坏,由它包含的子项地质因素加权(式2中的qij)平均值得到[10]。不同目标区域所使用的评价参数体系与参数取值标准对地质评价结果有直接影响。表1是基于成藏体系理论定义,应用于大港某区带地质评价的评价参数体系与评价规范[11],本文后续不确定性评价示例主要围绕表1的评价参数与评价规则定义展开(图2)。

图1 油气资源不确定性的渐进评价流程
(1)
(2)
式中:P表示评价对象地质风险评价结果;Pi表示单项成藏条件的成功概率;Pij表示子项成藏要素的地质成功概率;qij表示不同子项评价时所占的比重。
对各子项成藏地质因素评价的主观评价(也称“专家打分”),主要有两种方法:一是专家针对最新勘探资料的定性认知,直接设定其主观成功概率值;二是基于子项成藏地质因素的量化定义,根据表1中的评价规则进行线性插值来计算其评价值。不管何种模式,上述两种方式赋予子项成藏地质因素的评价值都是确定性的定值,往往对应的是子项成藏地质因素多种可能性中的一种;而在实际钻井前,受限于目标区域的勘探程度以及勘探资料可信度,对子项成藏地质条件的认知本身是不确定的。可见,上述计算规则规避了此问题,只能在多种情况中选一种,把不同子项要么高估、要么低估的结果通过式2、1传递到最终的地质风险量化评价结果上 —— 由于地质风险概率法提供的是单一的、确定性(“点估计”)评价结果,其蕴含的不确定性信息不够充分,在某种程度上会造成后续相关决策方案的片面或单一。当然,形成“点估计”的真正原因并不在于概率数学模型本身,而是对模型中涉及的地质评价因子的不确定性评价,缺少一种有效的量化方法。即,通过提升地质评价因子的不确定性表达与计算能力,地质风险概率法将会进一步有利于决策人员的综合评价,从而制订出合理的勘探部署决策方案。

表1 应用于大港某区带地质评价的评价参数体系
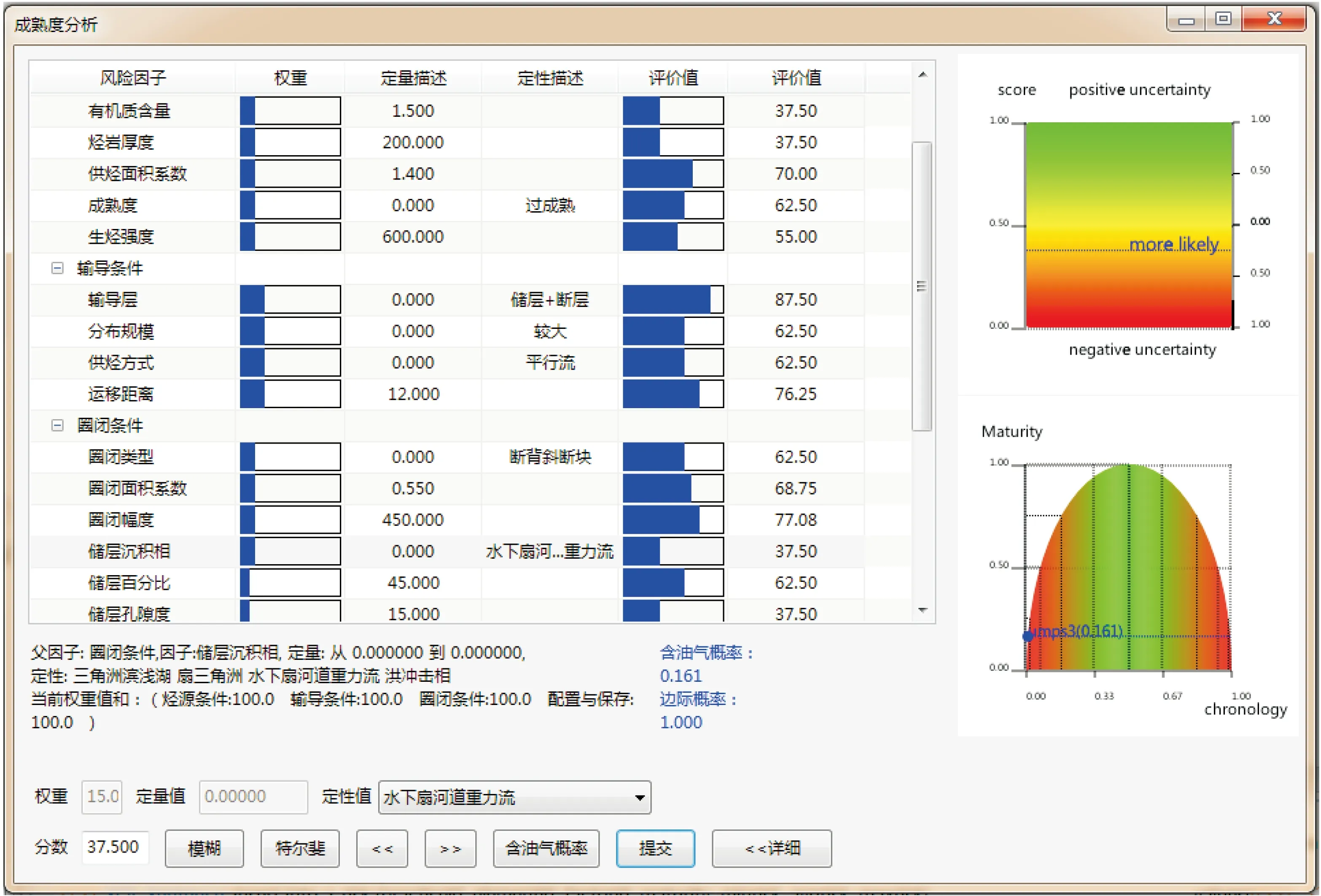
图2 评价参数主观推测面板与评价结果图形显示(PetroV)
针对上述问题,本文提出自信度转换模型来量化体现专家主观评价时的不确定性 ——“自信度高”意味着评价结果相对确定,“自信度低”则体现了评价结果的不确定性。也就是说,对不同地质评价因子的相关勘探资料的把握和认知程度,某种程度上反映了其对成藏贡献程度的不确定性描述(图2,右上图):主观推测结果接近分值1.0,对其“好”的成藏贡献的自信度越高,用绿颜色表示;同理,主观推测结果接近分值0.0,对其“破坏”成藏的自信度越高,用红颜色表示;而分值接近于0.5,体现了其相对“纠结”的成藏贡献度,自信度最低,用黄颜色表示。因此,通过双线性转换可把主观推测结果的0.5~1.0分值区间映射到0.0~1.0自信度区间,主观推测结果的0.0~0.5分值区间映射到-1.0~0.0的自信度区间。PetroV通过自信度转换,把子项成藏地质条件的主观评价结果转换为不确定性的量化描述,并结合三色可视化方案(红绿灯)用于后续地质评价系列结果图件,使得对地质评价结果一目了然(绿灯“行”,红灯“停”)。如,金之钧对地质风险结果进行了进一步量化区分,用以表征成藏成熟度并提出了对应的图版[12],利用上述双线性转换和三色表达,可以进一步将地质风险评价结果的不确定性转换为不同油气藏的成藏成熟度(图2,右下图,成熟度结果为0.21)。
基于自信度模型的不确定性量化转换,并不是直接建立在对子项成藏地质条件多种可能性的量化定义基础上,评价结果还是具有很强的主观随机性。本文通过借鉴模糊逻辑推理相关数学模型,在定义相关模糊(知识)规则基础上构建模糊推理流程,从基于单一可能性的纯粹定量分析过渡到基于多种可能性的定量分析,为地质评价的不确定性研究提供一种新的不确定性评价思路。
2 基于模糊逻辑推理的不确定性分析
得益于Zadeh(1965)、Mamdani(1975)等学者的研究成果[13],模糊逻辑推理被应用于多种信息处理系统,尤其是相关自动控制系统的研发。区别于传统集合理论的单值逻辑推理(“非此即彼”),模糊逻辑的多值逻辑推理可有效模拟不确定性推理过程。如,针对表1的“储层埋深”成藏地质因素,假定其埋深是1 400 m,根据图3a的单值推理模型,该子项成藏条件被直接归为埋深较浅的一类——“浅”意味着该子项主观评价结果高(表1的分值在0.75~1.0之间)。而根据图3b的多值推理,储层埋深1 400 m被转换成边界模糊定义:某种程度属于埋深“浅”一类(比重为0.65),同时某种程度又属于埋深“中等”一类(比重为0.35),通过加权平均合理地减低了评价值,客观体现了对该地质因子认知的不确定性。
除了有效处理边界模糊问题外,模糊逻辑推理也可很好地应用于基于定性描述(如,“低成熟”,“过成熟”,“未成熟”)或非数值型描述(如,排序问题)的地质评价因子的推理过程(图4)。可见,在刻画相关地质条件的不确定性以及基于对地下认知的定性描述进行推理等方面,模糊逻辑的多值推理具有很好的应用切入点[14-15]。本文遵循模糊推理逻辑推理的一般流程,将基于模糊逻辑推理的不确定性评价主要分为三步:(1) 定义每一地质评价参数的多值模型,也可看成对地下认知的不确定性量化处理;(2) 建立不同评价参数间的地质评价规则;(3)反模糊化推理结果,计算每一地质评价参数的定量结果。
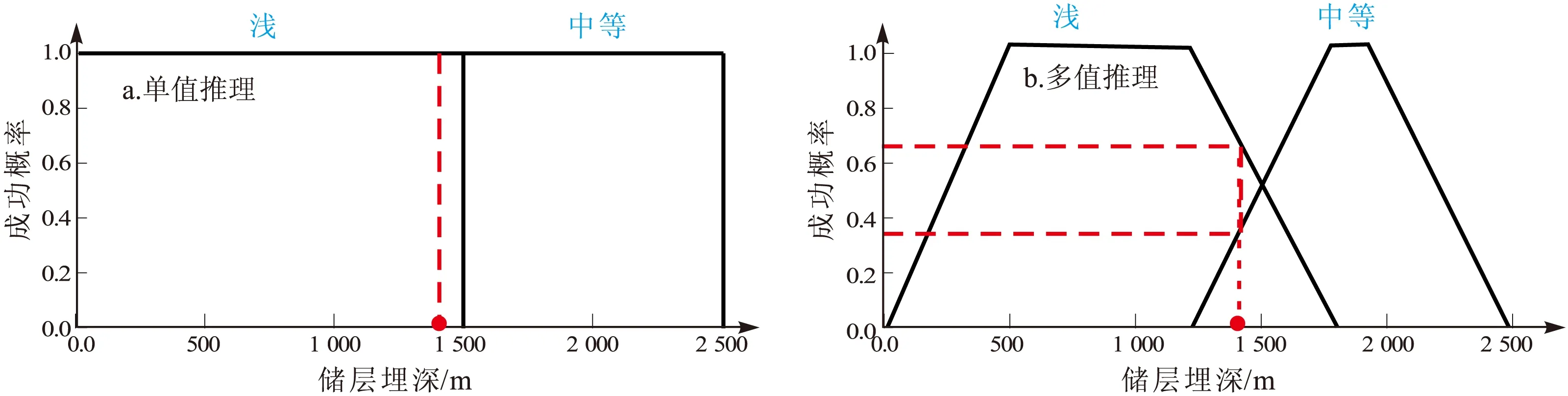
图3 评价参数单值与多值推理示意(PetroV)

图4 定性值域的评价参数的模糊成员函数示意(PetroV)
3 地质评价参数的模糊化
模糊化就是将每一地质评价参数的值域进行多种可能性区分,进而对应为系列模糊成员函数,利用模糊成员函数量化表述其多种可能性。此外,每个成员函数都有明确的名称定义,以便于后续建立基于定性描述的模糊评价规则[16]。模糊成员函数的纵轴取值范围为0.0~1.0,为不同成员函数(不同地下认知的可能性)与该评价参数的关联度描述,横轴对应的是该评价参数值域范围内的某一区间;不同成员函数的取值区间可以重叠(地下认知的不确定性),但关联度累加和为1.0。如,图3中“浅”成员函数对应的储层埋深为0~1 800 m,而“中等”成员函数对应的是1 200~2 500 m,它们重合部分的比重和为1.0。模糊成员函数的类型(几何形状)主要分为非参数型(图5a)和参数型(图5b,c)两类:基于非参数定义的几何形状,代表了单值推理数学模型(式3)。考虑到后续反模糊计算的简单与有效,参数化数学模型往往采用基于线性插值的梯形和三角形几何形状(式4、5)。当然,根据实际地质评价参数的分布特点,成员函数也可以直接被定义为某种概率分布曲线。
(3)
(4)
(5)
式中:x表示地质评价参数的评价值;μ(x)表示模糊成员函数;x1、x2、x3、x4表示当前评价参数的关键评价值,用于区分不同评价情形。
可见,PetroV对地质评价参数的模糊化就是将地下认知的多种可能性映射成系列模糊成员函数的边界重叠(图6),后续利用不同的模糊逻辑操作进行客观逻辑推理。“模糊化”的基本步骤是(图6):(1)识别每一地质评价参数的量化内容是数量定义(Rational)还是定性描述(Categorial),来指定其值域类型(Value Type);(2)选定三角(Triangular)还是梯形(Trapezodial)“概率”分布形态来约定成员函数类型(Function Type);(3)据表1中每一地质评价参数的不同“打分”值域区间对应不同成员函数,左、右调整现有值域区间,进一步区分出不同成员函数的确定性区间(Lower-Upper)和不确定性区间(Left-Lower, Upper-Right),其中不同成员函数的不确定性区间的叠合体现了对地下认知的某种程度的不确定性;(4)最后,为每个成员函数(地下认知)给出对应的定性地质评价结果(Geological Favorability),用于后续模糊评价规则的建立。
3.1 定义地质评价规则(模糊规则)
通过图6给出每一地质评价参数的多值模型后,定义系列地质评价(模糊或知识)规则是后续计算不确定性量化结果的充分必要条件。每一条地质评价规则采用的是专家系统中典型的IF-THEN范式,包括逻辑条件和结论两部分:逻辑条件的“主”、“谓”、“宾”分别对应“评价参数”、“模糊集合运算子”与“评价参数的某一成员函数”;结论部分(也称“地质评价结果”)被定义为面向所有评价参数的统一地质评价结果,其不同成员函数对应为表1中约定的不同“打分”区间,包括“很不好(unfavorable)”、“不好(questionable)”、“一般(neural)”、“好(encouraging)”、“很好(favorable)”5个评价层次。说明的是,在实际工作中,地质评价结果的评价层次可以灵活调整,以便更合理获取定量地质评价结论。

图5 3种典型成员函数数学模型

图6 定义地质评价因子多值模型面板(PetroV)
基于地质评价参数和统一地质评价结果的多值模型,模糊规则的解译或推理关键在于二者不同成员函数间逻辑运算子的合理运用。常见的模糊逻辑运算子主要包括:“求交”、“求和”、“求补”等(式6、7、8)。“求交”意味着取两个成员函数的最小值,“求和”意味着取两个成员函数的最大值,“求补”则意味着取某一成员函数的反值。在约定某一地质评价参数的地质认知(式6、7、8中的X)情况下,PetroV主要采用“求和”逻辑运算子来联合(Union)地质评价结果中的邻接成员函数图形, PetroV解译地质评价规则的过程如下:(1)基于地质评价参数的多值模型,计算该地质评价参数的“打分”结果,计算模式主要包括“单值推测”(图7a),“线性插值”(图7b)和“不确定性推测”(图7c,d);(2) 关联地质评价结果中的成员函数,将上述打分结果投影到该成员函数的纵轴和横轴上,形成以多边形形状表达(图7阴影部分)的评价结果;(3)针对不确定性推测关联的两个成员函数,采用“求和”联合阴影部分,形成最大可能的分值分布(图7c,d)。
μA∩B(x)=min{μA(x),μB(x)},x∈
(6)
μA∪B(x)=max{μA(x),μB(x)},x∈
(7)

(8)
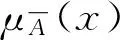
以图3“储层埋深”的多值模型为例,假定两条地质评价规则来进行不确定性计算(图7):第一条,如果储层埋深属于“浅”,那么其地质评价结果为“很好”;第二条,如果储层埋深属于“中等”,那么其地质评价结果为“好”。在计算(推理)过程中,除了可很好地兼容地质风险概率法的单值推理模式外,模糊逻辑推理还充分考虑了评价参数地下认知的不确定性。如,假设储层埋深为800m,那么可根据规则直接获取“很好”的地质评价结果(图7a阴影部分,且充满);假设储层埋深2 200m,那么可根据规则直接获取“好”的地质评价结果(图7b阴影部分,未充满);假设储层埋深1 300m或1 600m(图7c,d),则评价结果取决于“很好”与“好”成员函数的逻辑运算。可见,基于不同地质评价规则获取的地质评价结果并不是纯粹性的定量分值,而是具有一定分布区间的不规则几何形状。同时,评价结果的几何形状或分布趋势(“正向”或“负向”分布)也可作为后续该地质评价参数概率数学模型选择的依据。

图7 基于模糊规则的系列推理场景(PetroV)
3.2 反模糊化
通过解译不同地质评价参数的系列地质评价规则,地质评价结果并不是一定值,而是由不同成员函数联合形成的具有不同分布特点的联合多边形(图7阴影部分)。因此,如何利用适合的数学方法计算体现不同成员函数的综合贡献度(或单一评价值)变为关键 —— 需要通过系列反模糊化技术手段获取最终的地质风险分析的量化结果(质心法、奇异点法、最大值法等[17])。PetroV采用的是质心法,即,通过计算阴影多边形的质心,获取质心点的纵轴投影作为目标区域地质评价的风险分析结果。相对于自信度转换的不确定性表达,利用模糊逻辑推理相关数学模型获取的地质风险评价结果(反模糊化),在某种程度上是蕴含了不同评价参数自身地质不确定性的表达,进而通过式1、2可以获取相对客观的地质风险评价结果。问题是,该结果还是“点估计”评价结果,还不能够真正意义上为决策人员提供符合某种概率分布的地质风险评价结果。
4 基于蒙氏模拟的不确定性分析
理论上,蒙特卡洛方法的核心就是通过人为构造一合适的依赖随机变量(评价参数的地质评价结果)的概率模型,使某些随机变量的统计量为待求问题的解(式1中的独立事件连乘),进行大统计量的统计实验[18]。因此,最终不确定性表达的关键在于如何把每个评价参数的不确定性联合、衍变为目标区域综合地质评价结果的概率分布:(1)约定每一地质评价参数的不确定性定义(也称多值模型),并通过建立合理的地质评价规则来计算不确定性评价结果(阴影部分);(2) 根据评价结果(阴影)“分值”分布趋势(正向、负向还是对称),选择适合的随机数产生器,产生对应的分值概率曲线;(3)根据式1、2,将不同地质评价参数的概率“打分”曲线作为输入,同时可结合不同地质评价参数间的相关性,进行大统计量模拟计算,获取最终多分位地质风险评价结果。
蒙特卡洛模拟的效果“好”与“坏”与每个评价参数的评价结果的概率分布模型,或随机数产生器有直接的关系。PetroV基于模糊逻辑推理获取的评价结果的几何形状,为随机数产生器提供了合理的参考和约定。如,采用三角分布随机数产生器,通过5 000次随机采样,图7c和图7d的阴影部分合理地转换为分布趋势相同的图8a和图8b的直方图统计分布。在为每个评价参数选取合适的概率分布模型之后,本文利用式1、2,进行5 000次随机统计分析,基于直方图(分100组)统计获取的蒙特卡洛模拟结果能够很好地反映地质评价中的不确定性,包括“联合概率”分布曲线和7分位对应的地质风险量化评价结果(图9)。可见,相对于基于表1打分规则直接计算获取的单一地质风险评价结果(0.21,图2右侧下图),基于模糊逻辑推理,进而利用蒙氏模拟获取的结果具有更多的选择判断:大于50%的概率,风险评价值是0.22;大于90%的概率,风险评价值是0.1;大于10%的概率,风险评价值是0.38。
5 结论
油气资源评价中最确定的事情就是评价结果的不确定性。本文提出、引进的自信度转换、模糊逻辑推理和蒙氏模拟等技术,通过分层次刻画地质风险评价中的不确定性,目的就在于使得不同勘探阶段的评价结果的不确定性降到最低或最大可能地描述出来。在勘探阶段初期,自信度转换能够有效量化不同专家主观推断情形,可以较好地在最终地质评价结果中体现地质资料自身的不确定性、可信度等。随着勘探资料的丰富,通过建立地质评价参数的多值模型,能够客观表达对不同评价参数地下认知的不确定性,进而通过模糊逻辑推理计算关键地质评价因子的评价值,使得地质风险概率的计算结果蕴含了客观不确定性信息。基于模糊逻辑推理获取的地质评价参数“打分”分布趋势,合理约定不同地质评价参数评价结果的概率分布曲线,进而基于蒙氏模拟能够给出更加客观的地质评价的多分位评价值,使得决策人员在后续的勘探决策中能够充分考虑评价结果的不确定性。显然,在充分融合专家对目标区域深层次认知以及客观表达地下认知的不确定性的基础上,本文基于自信度转换模型、模糊逻辑推理和蒙特卡洛模拟等技术手段,除了显著提升地质风险概率法的“决策能力”外,更重要的是,为地质风险评价中的不确定性分析提供了新的研究思路。

图8 利用图7d的模糊概率原型进行5 000次随机取样的三角概率分布模型(PetroV)

图9 进行5 000次随机统计分析的地质风险不确定性体现(PetroV)
[1] 武守城.石油资源地质评价导论[M].北京:石油工业出版社,1994:292-294.
WuShoucheng.Introductionofpetroleumresourcesassessment[M].Beijing:PetroleumIndustryPress,1994:292-294.
[2] 国土资源部油气资源战略研究中心.新一轮全国油气资源评价[M].北京:中国大地出版社,2009:66-71.
StrategicResearchCenterofOil&GasResources,MinistryofLand&Resources.Thelatestnationalresourcesassessment[M].Beijing:ChinaUniversityofGeosciencesPress,2009:66-71.
[3] 郭秋麟,米石云.油气勘探目标评价与决策分析[M].北京:石油工业出版社,2004:21-22.
GuoQiulin,MiShiyun.Assesmentofpetroleumexplorationtargetandexplorationdecisions[M].Beijing:PetroleumIndustryPress,2004:21-22.
[4] 盛秀杰,金之钧,鄢琦,等.成藏体系油气资源评价中的统计方法体系[J].石油与天然气地质,2013,34(6):827-833.
ShengXiujie,JinZhijun,YanQi,etal.Statisticalmethodseriesfortheresourceassessmentofpetroleumaccumulationsystem[J].Oil&GasGeology,2013,34(6):827-833.
[5]RosePR.油气勘探项目的风险分析与管理[M].北京:石油工业出版社,2002:6-50.
RosePR.Riskanalysisandmanagementofpetroleumexplorationventures[M].Beijing:PetroleumPress,2002:6-50.
[6]OtisRM,SchneidermannN.Aprocessforevaluatingexplorationprospects[J].AAPGBulletin,1997,81(7):1087-1109.
[7]WhiteDA.Geologicriskingguideforprospectsandplays[J].AAPGBulletin,1993,77(12):2048-2061.
[8]HoughtonJC,DoltonGL,MastRF,eta1.U.S.GeologicalSurveyestimationprocedureforaccumulationsizedistributionsbyplay[J].AAPGBulletin,1993,77(3):454-466.
[9] 盛秀杰,金之钧,郭勤涛,等.油气资源评价一体化技术及软件实现的探讨[J].地质论评,2014,60(1):159-168.
ShengXiujie,JinZhijun,GuoQintao,etal.Discussiononintegratedresourceevaluationandsoftwaredevelopment[J].Geolo-gicalReview,2014,60(1):159-168.
[10] 金之钧 张金川.油气资源评价技术[M].北京:石油工业出版社,1999:66-71.
JinZhijun,ZhangJinchuan.Petroleumresourceassessmenttechniques[M].Beijing:PetroleumIndustryPress,1999:66-71.
[11] 陈善勇,金之钧,刘小平.黄骅坳陷第三系油气成藏体系定量评价[J].石油与天然气地质,2004,25(5):544-547,602.
ChenShanyong,JinZhijun,LiuXiaoping.QuantitativeevaluationofTertiarypetroleumaccumulationsystemsinHuanghuadepression[J].Oil&GasGeology,2004,25(5):544-547,602.
[12] 金之钧,张一伟,王捷,等.油气成藏机理与分布规律[M].北京:石油工业出版社,2003.
JinZhijun,ZhangYiwei,WangJie,etal.Hydrocarbonaccumulationmechanismsandoil/gasdistribution[M].Beijing:PetroleumIndustryPress,2003.
[13]ZadehLA.Fuzzysetsasabasisforatheoryofpossibility[J].FuzzySetsandSystems,1978,1(1):3-28.
[14]CarranzaE,HaleM.Geologicallyconstrainedfuzzymappingofgoldmineralizationpotential,BaguioDistrict,Philippines[J].NaturalResourcesResearch,2001,10(2):125-136.
[15]ChenHC,FangJH.Anewmethodforprospectappraisal[J].AAPGBulletin,1993,77(1):9-18.
[16]PassinoKM,YurkovichS.Fuzzycontrol[M].California:AddisonWesley,1998.
[17]RossTJ.Fuzzylogicwithengineeringapplications[M].NewYork:McGraw-Hill,1995.
[18]RobertCP,CasellaG.Montecarlostatisticalmethods[M].2nded.NewYork:Springer,2004.
(编辑 徐文明)
Uncertainty evaluation of petroleum risk assessment
Sheng Xiujie1, Jin Zhijun1, Xu Zhongmei1, Jiang Han2
(1.SINOPEC Petroleum Exploration & Production Research Institute, Beijing 100083, China; 2.Information Engineering Institute, China University of Geosciences (Beijing), Beijing 100083, China)
The margin and condition probability analysis is broadly applied to the geological risk evaluation for an immature play with joining the “success” probabilities subjectively specified for those independently involved geological factors. Considering that it is difficult to specify a reasonable scoring distribution curve for each geological factor, this method contributes a “point” estimation about whether there exists petroleum resource. Obviously, subjected to lack efficient ways to encode the information about geological multi-scene of subsurface and possibi-lities for each geological factor, the above crisp estimation conclusion would be generally either higher or lower. In order to enhance the capability of uncertainty expression of geological risk evaluation, this paper presents three heuristic mathematic models to deeply quantify the understanding of a geological expert and objectively delineate the possibilities of subsurface occasion, etc. Meanwhile, the uncertainty assessment methods discussed also de-monstrate a reasonable uncertainty evaluation process from subjective guess to objective prediction in order to shrink the uncertainty of evaluation as more as possible. Firstly, the double linear conversion between subjective inference for each factor and quantized confidence shares an efficient alternative to describe subjective uncertainty. Next, the specification of multi-value model and setup of corresponding fuzzy rules for each geological factor may accurately and honestly reflect the worldly uncertainty of subsurface multi-scene while matching the domain expert’s understanding as more as possible. At last, Montecarlo method randomly joins the objective uncertainty distribution curve of each factor and shares experts with quantiles evaluation which would benefit incoming reasonable exploration solution. As a conclusion, this paper not only investigates how to make full scale uncertainty evaluation for geological evaluation, but also expands a new horizon about geological risk uncertainty research.
confidence conversion; fuzzy logic; Montecarlo simulation; uncertainty evaluation; geological risk analysis; petroleum assessment
1001-6112(2014)05-0633-09
10.11781/sysydz201405633
2014-05-01;
2014-08-18。
盛秀杰(1973—),男,高级工程师,从事油气资源评价、专业应用软件开发等研究。E-mail: shengxj.syky@sinopec.com。
国家科技重大专项(2011ZX05005-001-004)资助。
TE122.3+5
A

