二阶时滞微分方程解的有界性研究
李文娟
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
二阶时滞微分方程解的有界性研究
李文娟
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
本文借助辅助泛函,得到了二阶时滞微分方程:x¨(t)+a(t)f(x˙(t))+b(t)g(x(t))+c(t)x(t-τ)+d(t)x(t-h)=0的解有界的判定方法.
有界性;时滞微分方程;辅助泛函;积分不等式
1 引言
文[1]
文[2]
本文的主要结果是给出二阶非齐次非线性时滞微分方程

的一切解均有界的判定准则.
其中a(t),b(t),c(t),d(t),f(u),g(u)均为连续函数,为常数f(0)=g (0)=0,τ≥0,h≥0为常数.

定理1
若系统1满足以下条件:

则系统1的一切解有界.

对后几项,因


从而x(t)最终有界.

其中a(t),b(t),ci(t),f(u),g(u)均为连续函数,f(0)=g(0)=0,τi≥0为常数.
系统(1)变为

推论1
若系统2满足以下条件:
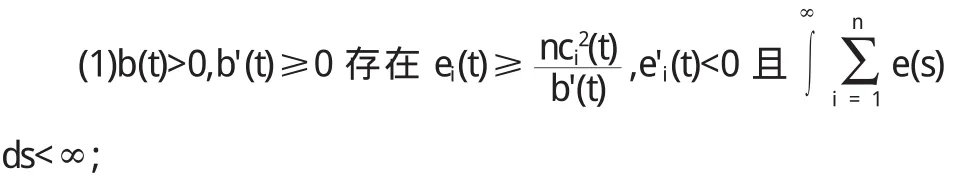
(3)a(t)≥0,f(y)sgny≥0
则系统2的一切解有界.
其证明过程类似于定理1.
定理2
若系统1满足以下条件:

则系统1的一切解有界.
证明

对V求导数,有:


从而x(t)最终有界.
推论2
若系统2满足以下条件:
(1)b(t)>0,存在ei(t)≥0,使得

则系统2的一切解有界.
考虑系统:

定理3
若系统(3)满足以下条件:

则系统(3)的一切解最终有界.
证明
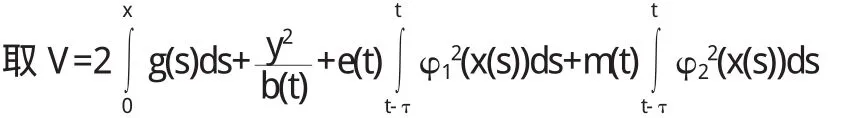
对V求导数,有:


对后几项,因

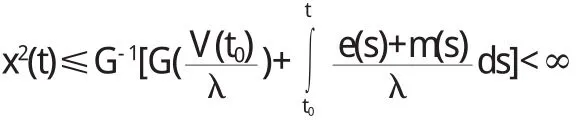
若系统(3)变为:

其中a(t),b(t),ci(t),f(u),g(u),φi(u)均为连续函数,为常数.

推论3
若系统4满足以下条件:

则系统(4)的一切解最终有界.
证明 类似定理3的证明.

定理4
若系统(5)满足以下条件:

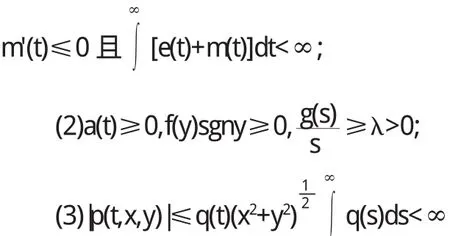
则系统(5)的一切解有界.

对V求导数,有:


从而x(t)最终有界.
若系统(5)变为:
其中a(t),b(t),ci(t),f(u),g(u)均为连续函数,f(0)=g(0)=0,τi≥0,为常数.

推论5
若系统(6)满足以下条件:

则系统(6)的一切解有界.
证明 类似定理4的证明
考虑系统:

其中a(t),b(t),c(t),d(t),f(u),g(u),φ1(u),φ2(u)均为连续函数,

定理5

则系统7的一切解有界.
证明


对V求导数,有:

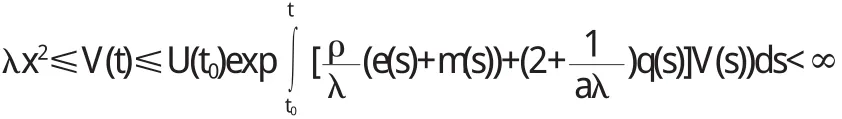
从而x(t)最终有界.
若系统变为

其中a(t),b(t),ci(t),f(u),g(u),φi(u)均为连续函数,为常数.
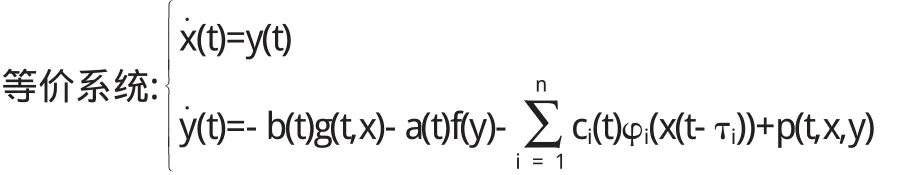
推论5

则系统8的一切解有界.
证明 类似定理5的证明.
〔1〕孟东沅.一类二阶泛函微分方程解的平方可积性和有界性[J].数学的实践与认识,2006,36(5):251-257.
〔2〕杨启贵.二阶非齐泛函微分方程解的有界性[J].数学的实践与认识,2000,30(2):226-231.
〔3〕Meng Fangwei,Quadratic integrability and boundedness of second order nonhommogenous linear differential equation[J],Sys.Sci.Math,15:1(1995)50-57.
〔4〕Sun Yuangong,Meng Fangwei,Quadratic integrability and boundedness for the solution of second order nonhommogenous linear differential equation[J],Ann. of Diff.Eqs,18:1(2002),58-64.
〔5〕李文娟.二阶非齐次泛函微分方程解的有界性[J].赤峰学院学报,2009,25(2).
〔6〕李文娟.具有偏差变元的积分微分方程解的有界性[J].内蒙古师范大学学报,2013,42(5).
O175.1
A
1673-260X(2014)08-0001-04

