基于模糊随机变量的资产组合选择模型研究
邓永辉
(湖南财政经济学院,湖南 长沙 410205)
基于模糊随机变量的资产组合选择模型研究
邓永辉
(湖南财政经济学院,湖南 长沙 410205)
本文利用随机变量表示各种投资的收益率,在概率理论和随机机会规划理论的基础上建立了投资组合的决策模型,导出与原问题有紧密联系的附属问题及求解这类问题的一种有效算法.
资产组合选择;模糊随机变量;隶属函数;测度空间
如何把投资资金分配到不同的资产中,以达到分散风险并确保收益的目的,这是资产组合选择(Portfolio selection)研究的问题.现实中由于证券市场中存在着很多种不确定因素,因此,Portfolio selection问题常常伴随着许多的不确定性.以概率论为基础,从上个世纪60年代开始,许多学者对随机资产组合选择理论进行了深入研究,取得了显著的研究成果.例如,Markowitz提出用资产组合收益的数学期望和方差度量投资收益和风险,提出了资产组合选择问题的均值方差模型[1].此外,Roy从不同的思路提出了资产组合选择的安全第一模型[2].实际上,无论是均值方差模型,还是安全第一模型,以及后来诸多学者提出的扩展模型,这些资产组合选择模型都有一个共同的前提条件,那就是假设证券市场中的各种不确定性事件,不论其表现形式与性质如何,都是受到随机因素影响的结果.然而,实践经验告诉我们,事件的不确定性主要有两种不同的表现形式,即随机性和模糊性随机性.随机性是指事件是否发生的不确定性,而模糊性则是指事件本身状态的不确定性.
在绝大多数资产组合选择模型中,考虑到诸多随机因素的影响以及投资专家的经验、知识和判断在证券投资分析中发挥的不可忽视的作用,各证券的收益率被假设为随机变量或者模糊变量.然而,正是因为证券市场中随机性和模糊性这两种不确定性同时并存,所以单单从随机不确定性或者从模糊不确定性的角度都无法全面的描述证券市场中存在的多重不确定性,如果将随机因素的影响以及投资专家的经验和知识这两方面结合起来考虑,无疑对证券收益率的估计会更加合理,同时有助于建立更加符合实际情况的资产组合选择模型,从而制定出更合理的投资策略.本文在前人研究的基础上,假设投资者的投资收益为模糊随机变量,以模糊随机变量为研究工具,建立模糊随机环境下的资产组合选择模型,并利用参数二次规划找到了解决原问题的一种算法.
1 模糊随机变量
由于实际情况中随机因素和模糊信息常常同时出现,而且人们无法将随机性与模糊性分离出来,因此,他们假设资产的未来收益率为模糊随机变量.
定义1设(Ω,FΩ,P)为一概率空间,(Θ,FΘ)为一测度空间,其中,Ω为集合,Θ为模糊集,FΩ和FΘ是σ-代数,P为概率测度,模糊变量X是Ω到Θ的可测映射.即∀A∈FΘ,都有{w|X(w)∈A}∈FΩ.
定理1设x是概率空间(Ω,FΩ,P)到测度空间(T,FT)的一个可测映射,X为Ω到Θ的映射,如果存在一个双向映射h:Θ→T,则存在一个测度空间(Θ,FΘ),且(Ω,FΩ,P)到(Θ,FΘ)的映射X是模糊随机变量.
推论1 设X是Ω到Θ的映射,假设∀w∈Ω,模糊集合X(w)的隶属函数μX(w)关于函数f(u;θ)都有μX(w)=f(u;x(w)).其中,θ是参数向量,当θ1≠θ2时,f(u;θ1)≠f(u;θ2).因此X是模糊随机变量.
2 模糊随机资产组合选择模型
假设资产的未来收益率为模糊随机变根据单因素模型[3],可知:

其中dj表示资产j的收益率,rj表示无风险资产的收益率,rm表示市场组合的收益率,且为资产j的 β值,αj为资产j的α值(1-βj)则有
假设dj=αj(w)+βjrm,其中αj(w)为模糊随机变量,且有以下形式的隶属函数

其中L为基准函数,αdj(w)服从正态分布

当f(0)=1,g(z)为连续单调递增的函数时,l(t)也是连续单调递增的函数.则模糊随机资产组合选择模型为是随机事件,t∈[0,1]为投资者事先给定的概率置信水平值.

3 模糊随机资产组合选择模型的最优解




可将M2化为:

其中Kt与t的标准正态分布函数F的关系为Kt=F-1(t) >0,分别通过最优值x*和h*可以求出模型M的最优解.
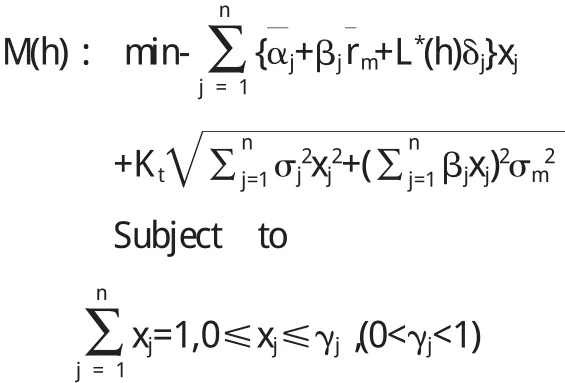
x(h)和Y(h)分别是M模型的最优解中的最优值,又由于目标函数P(h)是关于x严格凸函数,因此在最优解中x(h)是唯一确定的.
〔1〕Markow itzH.Portfolioseleetion.Journal of Finanee,1952,7:7-91.
〔2〕Roy A.D.Safety-first and the holding of assets.Econometrics,1952.20:431-449.
〔3〕W.F.Sharpe,“Capital Asset Prices:A Theory of Market Equilibrium under Conditions of R isk,”J.O f Finance,Vo1.19,1964,pp.425-442.
〔4〕邓永辉,邓永红.溶质运移模型的有限元数值解[J].海南大学学报自科版,2011(1):25-28.
O211;O242.1
A
1673-260X(2014)10-0011-02
湖南省社科基金项目(K201110)

