半单环在环类刻画中的某些应用
李艳午, 刘钢
(1.芜湖职业技术学院,安徽 芜湖 241000;2.宿州学院数学与统计学院,安徽 宿州 234100)
半单环在环类刻画中的某些应用
李艳午1, 刘钢2
(1.芜湖职业技术学院,安徽 芜湖 241000;2.宿州学院数学与统计学院,安徽 宿州 234100)
首先利用正则环,对半单环进行了一个新的刻画;然后,构造了半单环成为单位正则环的一系列条件,在此基础上对单位正则环进行了半单环意义下的两个刻画;最后,通过构造Artin环到半单环的条件,将半单环的有关结论推广到Artin环中.
半单环;正则环;单位正则环;Artin环
1 引言
一个左R-模M叫做半单的,如果M 的任意R-子模都是M的直和项;环R叫做半单环,如果每个左R-模都是半单的.如同半单模在模论中扮演着十分重要的角色一样,半单环在环论中占有重要的地位.因此,半单环越来越被一些代数工作者所重视,大部分环论的经典著作[1-3]都对半单环进行了深入探讨和经典刻画,一些重要的环类也往往都与半单环有着密切的联系,如SF-环[4].
环R中的一个元素a称为单位正则的,如果存在一个单位(即可逆元)u∈R,使a=aua;称R为单位正则环,如果R的每个元素都是单位正则元[2].单位正则环与环的稳定度和模的消去性都有着密切的关系,这是近年来继正则环后又一个重要的环类,吸引着环论研究者的兴趣.文章首先利用正则环,对半单环进行了一个新的刻画;然后,构造了半单环成为单位正则环的一系列条件,在此基础上对单位正则环进行了半单环意义下的两个刻画;最后,通过构造Artin环到半单环的条件,将半单环的一系列结果推广到Artin环中.
本文中的环,都是有单位元的结合环,模都是酉模;a∈R,l(a)表示元素a在环R中的左零化子,r(a)表示元素 a在环 R中的右零化子.U(R)是环 R的单位元素的集合.J(R)和Soc(RR)(Soc(RR))分别表示环R的Jacobson根和RR(RR)的基座.其余符号均参照文献 [1].
2 主要结果及证明
众所周知,Artin半单环是正则环[5-6],但正则环不一定是半单环;半单环既是Artin环又是Noether环,但反之Artin环和Noether环又都不一定是半单环,而下面的结果弥补了这一缺憾.
定理 1对于正则环R,下列各条等价:
(1)R是半单环;(2)R是Neother环;(3)R是Artin环.
证明(1)⇒(2),(1)⇒(3).由半单环的性质易得.
(2)⇒(1).如果R是Neother环,那么R满足主左理想的升链条件.令S=Soc(RR),下面证明S=R.如果SR,那么存在R的极大主左理想I,使得S⊆I⊂R,并且I在R中是本质的.又由于R是正则环,所以存在e=e2∈R,使得I=Re,从而I是有限生成的.故正和列:是有限相关的,所以R/I是有限相关的平坦模.再根据文献[8]中的TH3.16,R/I是投射左R-模,从而是RR的直和项.而这与I在R中是本质的相矛盾.所以,S=R.故,R是半单环. (3)⇒(1).与(2)⇒(1)类似,可证.
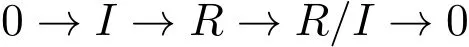
显然,单位正则环都是正则环,而反之不真.但是,根据文献[7]中推论2.4,比正则环条件稍强的强正则环是单位正则环.既然半单环都是正则环,所以半单环距单位正则环仅一步之遥.下面的定理就是考虑极大左理想的性质,从几条不同的渠道铺设由半单环到单位正则环的路径.
定理 2一个半单环R,如果又满足下列条件之一:
(1)R的每个极大左理想都是理想;
(2)R的每个极大左理想在R中都是本质的;
(3)R的每个极大左(右)理想都是广义弱理想.
那么,R是单位正则环.
证明首先由半单环的正则性知,环R是正则的.
如果条件(3)成立,那么根据文献[9]中定理11,可证环R是强正则环,故R是单位正则环.
如果aR+bR=R,存在x∈R使得a+bx是一个单位,那么称环R具有稳定度1(见文献[2]).下面就由半单环在一定条件下的单位正则性,导出其具有稳定度1的性质.
推论 1一个半单环R,如果又满足下列条件之一:
(1)R的每个极大左理想都是理想;
(2)R的每个极大左理想在R中都是本质的;
(3)R的每个极大左(右)理想都是广义弱理想;
那么,R具有稳定度1.
证明首先,根据定理2知环R是单位正则环.令aR+bR=R,a,b∈R,则对某个J,有

进一步,令K={r∈R|ar=0},则有RR=K⊕L,这里L∼=aR,再根据文献[2]中定理4.1,知K∼=J.因此,存在c∈R,使得cL=0,而且由c所决定的左乘导出了KJ上的一个同构.由于cR=J≤bR,所以存在某个 y∈R,使得c=by.同理,由a所决定的左乘导出了LaR上的一个同构.因为aK=cL=0,由此推出由a+c所决定的左乘导出了L⊕K=RRaR⊕J=RR上的一个同构.所以,a+by=a+c是R中的一个单位,即环R具有稳定度1.
下面的定理将从有限生成投射模的消去性质,对单位正则环进行有限生成投射模消去意义上的刻画.
定理 3设 R是一个半单环,则 R是单位正则环当且仅当对所有有限生成投射 R-模A,B,C,由A⊕B∼=A⊕C都可以推出B∼=C.
证明一方面,如果对所有有限生成投射R-模A,B,C,由A⊕B∼=A⊕C都可以推出B∼=C,那么根据文献[2]中定理4.1,由模的这种消去性推出了R的单位正则性.
另一方面,如果R是半单的单位正则环,令A,B,C是有限生成投射左R-模,并且A⊕B∼= A⊕C,那存在正整数n,使得A是nRR的一个直和项,这里nRR⊕B∼=nRR⊕C.通过归纳,可以证明n=1的情形.假设RR⊕B∼=RR⊕C,根据文献[2]中定理2.8,给出了一个分解RR=R1⊕R2,B=B1⊕B2,使得
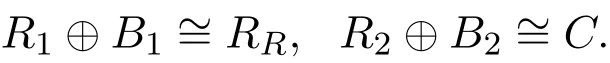
由于R1⊕B1∼=RR=R1⊕R2,所以B1∼=R2,于是
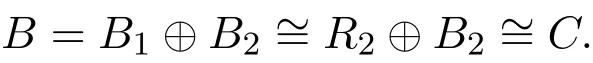
推论 2设R是有稳定度1的半单环,M是R上的有限生成投射模,则EndR(M)是单位正则环.
证明如果R是有稳定度1的半单环,那么由R的正则性知对任意的a∈R,存在x∈R使得a=axa.显然,aR+(1−ax)R=R,于是存在y∈R使得a+(1−ax)y是一个单位,从而存在u∈R使得[a+(1−ax)y]u=1.所以,
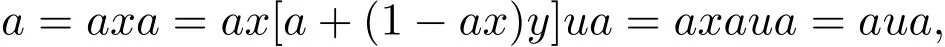
即R是单位正则环.最后,根据文献[2]中推论4.7,即证R(M)是单位正则环.
定理 4设R是一个半单环,I是R的双边理想,则R是单位正则环当且仅当下列两条同时成立:
(1)R/I是单位正则环
证明一方面,如果R是单位正则环,那么根据单位正则环的性质定理即[2]中定理4.1,即可得到结论(1)和结论(2).
另一方面,如果环 R满足条件 (1)和条件 (2).那么根据半单环的正则性,给定幂等元a,b∈R使得aRbR,由条件(1)可得(R/J)∼=(R/J),因此
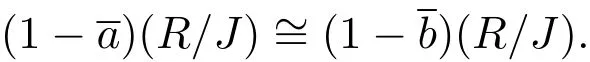
根据文献[2]中命题2.19,存在分解

使得A1∼=B1而A2=A2J,B2=B2J.于是,存在幂等元e,f∈R使得
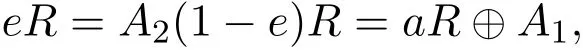
而使
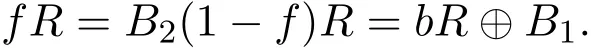
那么e,f∈J,并且(1−e)R∼=(1−f)R,从而根据条件(2)得eR∼=fR,于是(1−a)R∼=(1−b)R,因此R是单位正则环.
定理 5设R是左Artin环,则R只要满足下列条件之一:
(1)不包含非零的幂零左理想;
(2)对任意x∈R,xRx=0⇒x=0.
就有:
(a)环R的总体维数等于0;
(b)对任意左R-模M,M 既是投射模又是内射模;
(c)由左R-模构成的短正和列都可裂;
(d)环R的诣零根等于零;
(e)存在R的有限个双边理想Ri,i=1,2,···,n,n<∞,使得
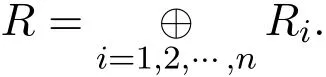
证明根据文献[1]中习题13,8(2)知,当R是左Artin环并且满足条件(1)和条件(2)时,R就是半单环.再根据文献[3]中定理 12和定理13对半单环的经典刻画,即可得到结论 (a)-(e).与半单纯环关系密切的环是本原环,即 J(R)=0的环,它可以看成是半单纯环概念的推广,它是除环上的线性空间的线性变换完全环的一个稠密子环.根据文献[10]中推论2.4.14,半单环等价于半本原的阿丁环,所以有:
注 1把定理[7]中的条件(1)和条件(2)改为R是半本原的,同样得到结论(a)-(e).
[1]Anderson F W,Fuller K R.Rings and Categories of Modules[M].Berlin Heidelberg:Springer-Verlag,1974.
[2]Goodearl K R.Von Neumann Regular Rings[M].2nd ed.Florida:Krieger Publishing Company Malabar, 1991.
[3]周伯埙.同调代数[M].北京:科学出版社,1998.
[4]李艳午,程海霞.SF-环的内射性[J].纯粹数学与应用数学,2012,28(1):17-24.
[5]Faith C.Algebra II:Rings Theory[M].Berlin Heidelberg,Springer-Verlag,1976.
[6]Fisher J.W.Von Neumann Regular Rings Versus V-rings,in“Rings Theory Proceedings of the Oklahoma Conference”[C]//Lecture Notes in Pure and Appl.Math..New York:Dekker,1974(7):101-119.
[7]李艳午,储茂权.Morphic Rings and regular Rings[J].安徽师范大学学报:自然科学版,2010,33(4):313-316.
[8]Rege M B.On Von Neumann regular rings and SF-rings[J].Math.Japonica,1986,36(1):927-936.
[9]周海燕,王小东.Von Neumann正则环和左SF-环[J].数学研究与评论,2004,24(4):679-683.
[10]陈家鼐.环与模[M].北京:北京师范学院出版社,1989.
Some applications about semisimple rings in the characterization of rings
Li Yanwu1,Liu Gang2
(1.Wuhu Vocational College of Technology,Wuhu 241000,China; 2.College of mathematics and statistics in Suzhou institute,Suzhou 234100,China)
Firstly,a new characterization of semisimple rings was obtained in In the sense of regular rings. Secondly,we constructed a series of conditions which from semisimple rings to unit regular rings and on which two characterizations were obtained about unit regular rings in terms of semisiple rings.Finally,by constructing the conditions that from Artin rings to semisimple rings,a series of results about semisimple ring were pushed to Artin rings.
semisimple rings,regular rings,unit regular rings,Artin rings
O153.3
A
1008-5513(2014)02-0149-05
10.3969/j.issn.1008-5513.2014.02.005
2013-12-27.
安徽省2013年省级自然科学研究项目(KJ2013B348);2011年度安徽省教育科学规划项目(JG11372);芜湖职业技术学院2013年院级教学研究项目.
李艳午(1975-),硕士,副教授,研究方向:环论与同调代数.
2010 MSC:16G10,16E10

