一种基于声道的无线通信模型

刘建华, 张雁冰

(1.西安邮电大学 信息中心, 陕西 西安 710121; 2.西安邮电大学 计算机学院, 陕西 西安 710121)

一种基于声道的无线通信模型

刘建华1, 张雁冰2

(1.西安邮电大学 信息中心, 陕西 西安 710121; 2.西安邮电大学 计算机学院, 陕西 西安 710121)

针对目前物联网无线通信技术硬件成本高且协议栈复杂的问题，提出一种基于声道的无线通信模型。该模型利用多频频移键控在声道上进行调制，采用瞬态同步技术以及谐波纠错技术保证在低运算能力情况下的实时性解码需求。实验结果表明，与现有的物联网无线通信技术相比，新模型的软件复杂度和部署复杂度较低，成本低廉，性能良好。

声道通信；无线通信；瞬态同步；谐波纠错

在当前物联网应用中，传感器节点的无线通信模块成本普遍较高，不便于大规模部署应用[1],且由于传感器节点普遍缺乏输入/输出(Input/Output, I/O)交互支持，配置提前内置，不便于灵活部署应用。

对于基于声道的无线通信，国内外学者做出了大量的研究。文[2]采用复杂重叠变换对信息进行调制，并通过声音进行传输。文[3-4]采用手机的扬声器和麦克风，在16 000～20 000 Hz的频段上进行了低速率通信的研究，并对音频信道进行了划分，满足了多个设备的通信需求。文[5]在声道噪声和环境噪声的干扰下进行了声道通信的研究。

目前学者们的研究主要集中在声道上信息的编码算法以及调制算法上，对于实际的应用场景考虑不足。采用扬声器和麦克风设备进行声道通信时，由于设备的品质不同，通信过程中信号会产生不同程度的瞬态失真、谐波失真、衰退和反射，影响通信情况。

本文拟提出一种基于声道的无线通信模型，针对实际应用场景中的信号失真、衰退和反射等问题，结合通信信道和设备运算能力的特点，采用瞬态同步以及谐波纠错等技术，以求满足在低运算能力情况下的实时性解码需求，并降低误码率。

1 声道通信模型

一个典型的声道通信模型如图1所示。原始声音数据通过数模(Digital/Analog, D/A)放大器后，通过扬声器进行发送。在声道的传输后，经过麦克风接收，最后通过低通滤波器后转变为接收声音数据。

图1 声道通信模型

1.1 通信协议

对于基于声道的通信，目前没有统一的通信标准。此处采用改进后的高级数据链路控制协议(High-speed Digital Subscriber Line, HDLC)[6]作为通信协议(图2)，它由帧头、设备地址、控制、信息、帧校验以及帧尾组成。帧头字段和帧尾字段由特定频率的声音组成；设备地址字段用于一对多，多对多之间的通信需求；控制字段用于多个频段之间的调度与控制，以及信息的标识；信息字段包含了三个通信信道，各由8位组成；帧校验字段采用16位循环冗余校验码(Cyclical Redundancy Check, CRC)[7]，对整个数据帧进行校验。

图2 声道通信协议

常见扬声器工作频率为20～20 000 Hz，麦克风的最大采样频率一般为44 100 Hz，根据采样定理，能被还原的最大声音信号的频率为22 050 Hz,但由于部分麦克风对高音部分进行了滤波降噪，收到的超过11 000 Hz的信号能量会非常低。此外，声道中最大的噪音源来自于人声，人声频率为60～1 200 Hz[8]， 因此，采用1 200～10 400 Hz作为通信频段。其中1 200～1 990 Hz作为控制字段，2 000～4 760 Hz为低通信频段，4 800～7 560 Hz为中通信频段，7 600～10 360 Hz为高通信频段。

1.2 调制与解调

对信息进行调制，主要是在三个通信信道上根据频码映射表进行多频频移键控(Multi-Frequency Shift Keying, MFSK)[9]。通过软件将特定频率的正弦波信号进行脉冲编码调制(Pulse Code Modulation, PCM)[10]后，通过扬声器发出。当麦克风收到声音后，将采样后的信号通过快速傅里叶变换(Fast Fourier Transformation, FFT)[11]得到信号分量，通过频码映射表进行解调。

一个三通道的MFSK信号可以表示为

x(t)=A[sin(2πf1t)+sin(2πf2t)+sin(2πf3t)],

(1)

其中A为信号的振幅,fi(i=1,2,3)分别为3个信号的频率。一个完整帧时域信号图如图3所示。

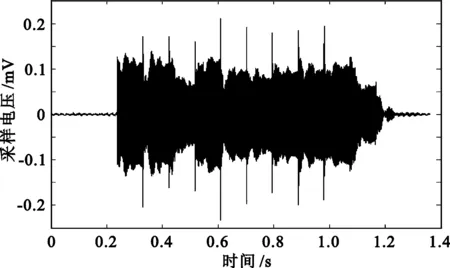
图3 完整帧时域信号

解调过程将由扬声器采集到的数字信号，选取FFT计算结果中最大的频谱分量，通过频码映射表还原得到原始信息。为了方便计算，通常采取2n个点进行计算。FFT的分辨率为

(2)

其中fs为信道最大频率，n为点数。取n=2 048，由式(2)得r=10.77Hz。频码映射表中相邻码元间的频率差为10.77Hz。因各码元由8位组成，故每个通信频段的宽度为2 756.25Hz。

1.3 传输速率

基于声道的数据传输速率为

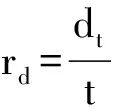
(3)

其中t为时间，dt为在时间t下传输的总比特数,且

(4)

其中N为信道总数，nb为单个码元的比特数,因此

此传输速率较低，适合于系统配置、人机I/O交互、以及低速数据的传输。

2 信息传输流程

对信息的传输主要分为编码部分和解码部分，如图4和图5所示。

图4 信息编码过程

图5 信息解码过程

编码过程中，对原始数据加入帧头、帧尾、校验码、设备地址、控制帧进行数据帧封装，根据频码表进行映射后，加入瞬态同步信号，通过脉冲编码调制，最后由扬声器产生声音信号。解码过程与之相反，由麦克风采集到声音信号后，对帧头进行检测，并通过瞬态同步技术进行帧的定位与同步，对信号进行滤波去噪后，采用快速傅里叶变换进行信号分析，并采用谐波纠错技术进行码元纠错，然后根据频码表进行映射。同时检测帧尾，获取整帧信号后，采用CRC进行校验，最后得到原始数据。

2.1 瞬态同步技术

电声换能器是将电信号利用机械震动转换为声能的器件，如扬声器。由于机械震动相对于电信号的延迟，不可避免的会产生瞬态失真(TransientIntermodulationDistortion,TIM)[12]。尤其是在调制的过程中，相邻码元间会产生较大的瞬态失真。

在信息解码过程中，需要对码元进行定位和分段。虽然可以在频域对信号进行分段，但这需要较高的计算开销。为了降低计算成本，在此给出一种时域的瞬态同步技术。

扬声器在时间段t中的机械位移为[13]

(5)

其中A0为相对于扬声器振膜平衡位置的最大振幅，r为总电阻值，s为振膜的柔韧度，m为系统总质量，θ为相位。为了获得最大程度的位移d，即瞬态失真，需要在短时间内发生较大的振幅差。瞬态失真信号可构造为

x(t)=AminΔt1+AmaxΔt2+AminΔt3。

(6)

其中Amin和Amax分别为信号的最低和最高振幅，Δti(i=1,2,3)为最高、最低振幅间的时间间隔。普通帧信号与加入了瞬态失真的帧信号如图6所示。

(a) 普通帧信号

(b) 瞬态失真帧信号

解码过程，当在Δt的时间内，信号的采样幅值同时超过上下阈值δ，即可对码元进行定位与同步。

2.2 谐波纠错技术

由于电声转换器中的放大器不够理想，放大曲线中存在非线性部分，导致谐波失真(TotalHarmonicDistortion,THD)[14]，尤其是二次谐波和三次谐波。谐波对FFT的分析带来很大的干扰。设理想放大曲线为y=x，y(x)为失真后的放大曲线，则放大电路的失真面积S可表示为

(7)

对y(x)进行傅里叶展开可得

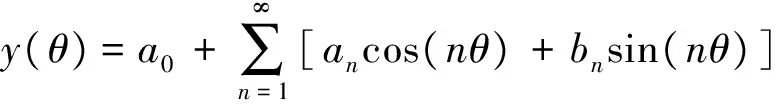
(8)

其中

θ=ωt,

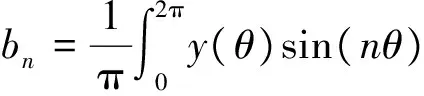
(9)

不妨设

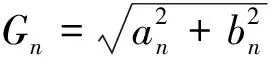
则n次HDn谐波可表示为

(10)

将调制信号表示为

(11)

并将式(8)(9)(11)代入式(7)可得

(12)

考虑上式中第三部分积分为0，an只有当n=2k时不为0，因此式(12)可改写为

(13)

将式(10)代入上式,得到

(14)

上式反映了偶次谐波失真与放大曲线失真面积之间的关系。

另设

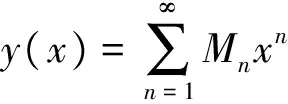
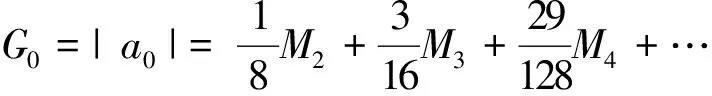
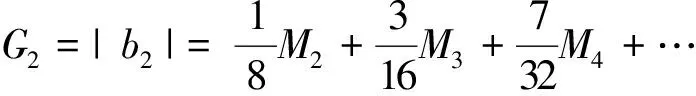
(15)

代入式(10)可得

HD0≈HD2，

再次代入式(14),可得

此即二次谐波失真与放大曲线失真面积之间的关系。

构造

Yr(x)=Y(X)-Y(-X),

其中Y(X)为失真后的信号。因推导过程类似，这里不再赘述，仅给出奇次谐波失真与放大曲线失真面积之间的关系式

(16)

三次谐波失真与放大曲线失真面积之间的关系为

S≈HD3。

图7为1 200 Hz码元信号经过传输后的频谱分析图，图中2 400 Hz和3 600 Hz分别为该码元的二次谐波以及三次谐波分量。

图7 信号频谱分析

对于给定的扬声器，其二次谐波和三次谐波可以根据其放大曲线推出,因此可以作为原始码的纠错码使用。

3 信道噪声分析

与高频无线通信相比，基于声道的无线通信模型受到自然噪声的干扰较大，且噪声的主要成分为大气噪声，其次是人为噪声[15]。

3.1 大气噪声

大气噪声的来源主要是大气层中的雷电活动。据统计，在大气层中，每秒会发生约2 000次放电现象。在低频频段中，雷电的衰减很小，且传播距离很远。大气噪声主要为脉冲型非高斯噪声。

根据Class A模型[16],大气中脉冲型非高斯噪声的概率密度函数可表示为

(17)

其中

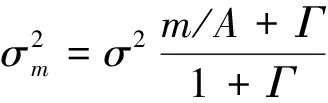
(18)

而A为脉冲的幅值，Γ为高斯噪声和脉冲噪声的功率比，σ2为噪声总功率。

由文[17]的数据得，在一个比较好的大气噪声模型中，有

A=0.25，Γ=2，

此时，Class A分布的概率密度函数如图8所示。

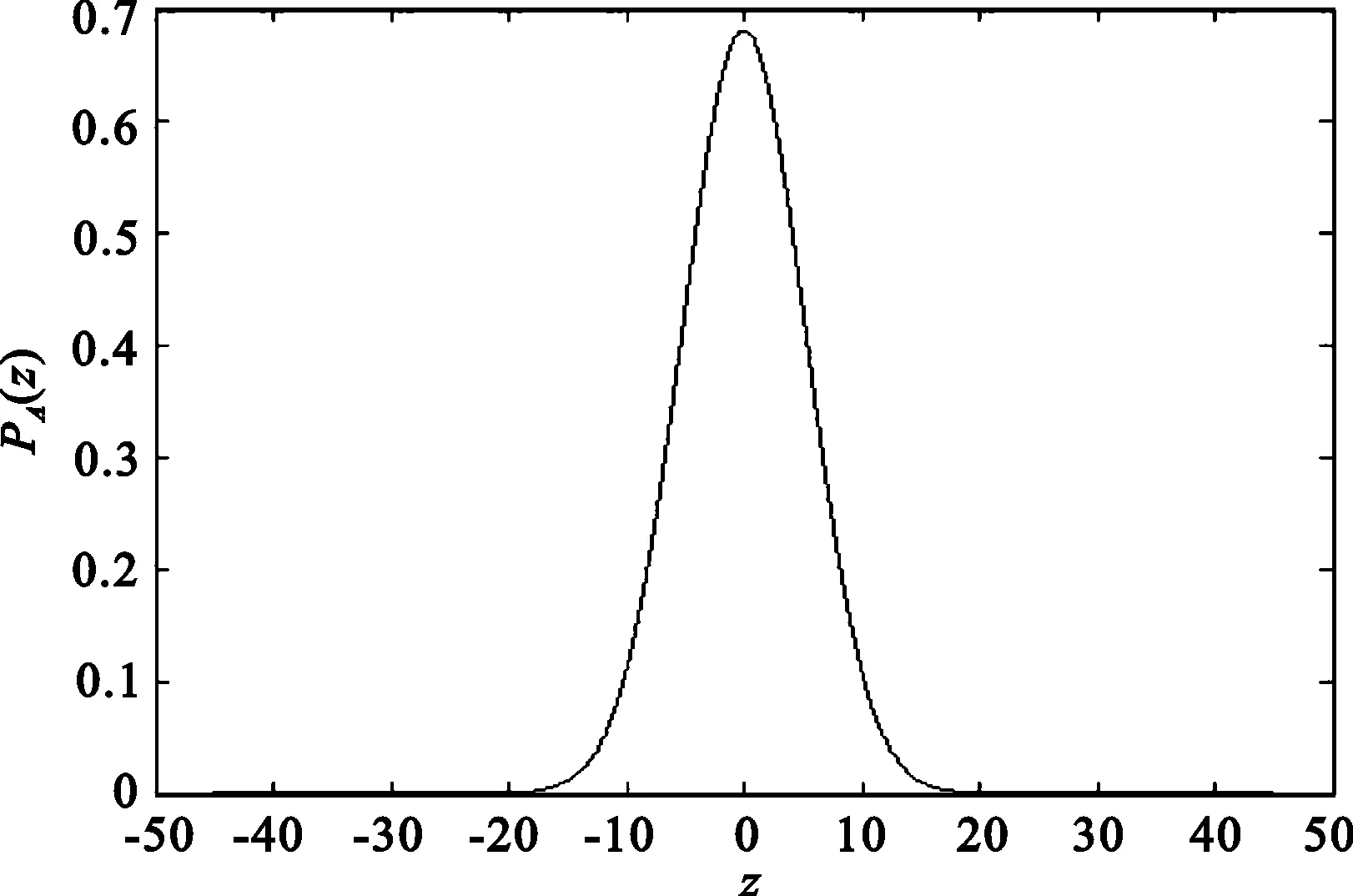
图8 Class A模型概率密度函数

3.2 人为噪声

人为噪声与环境的关系很大。从地点来看，人为噪声在安静区、商业区和工业区有很大差别；从时间来看，不同时间段的人为噪声是不一样的。因此对于人为噪声而言，其变化是随机的。ITU-R的报告表明[18]，人为噪声强度在地点上近似于对数正态分布。

对于对数正态分布，其概率密度函数可表示为

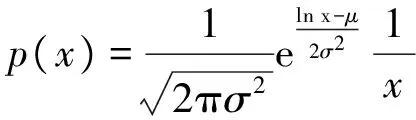
(19)

根据ITU-R的建议，取

μ=0.886,σ=0.463,

此时，对数正态分布的概率密度函数如图9所示。

图9 对数正态分布概率密度函数

4 实验结果

4.1 通信实验

实验采用Lenovo手机的麦克风模块和电脑在近距离，侧面，远距离，固态传播介质以及遮挡情况下进行了通信。实验环境如图10所示。

图10 通信实验环境

4.1.1 近距离通信

近距离通信(反射测试)的时域信号与单个码元信号频谱分析如图11所示。由于声波部分被反射，因此信号能量比侧面通信低,但不影响通信质量。

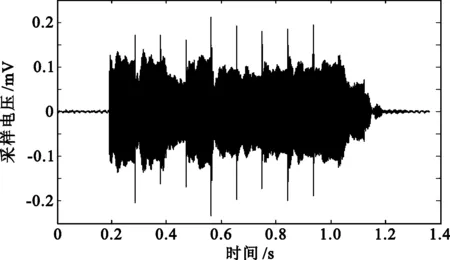
(a) 通信时域

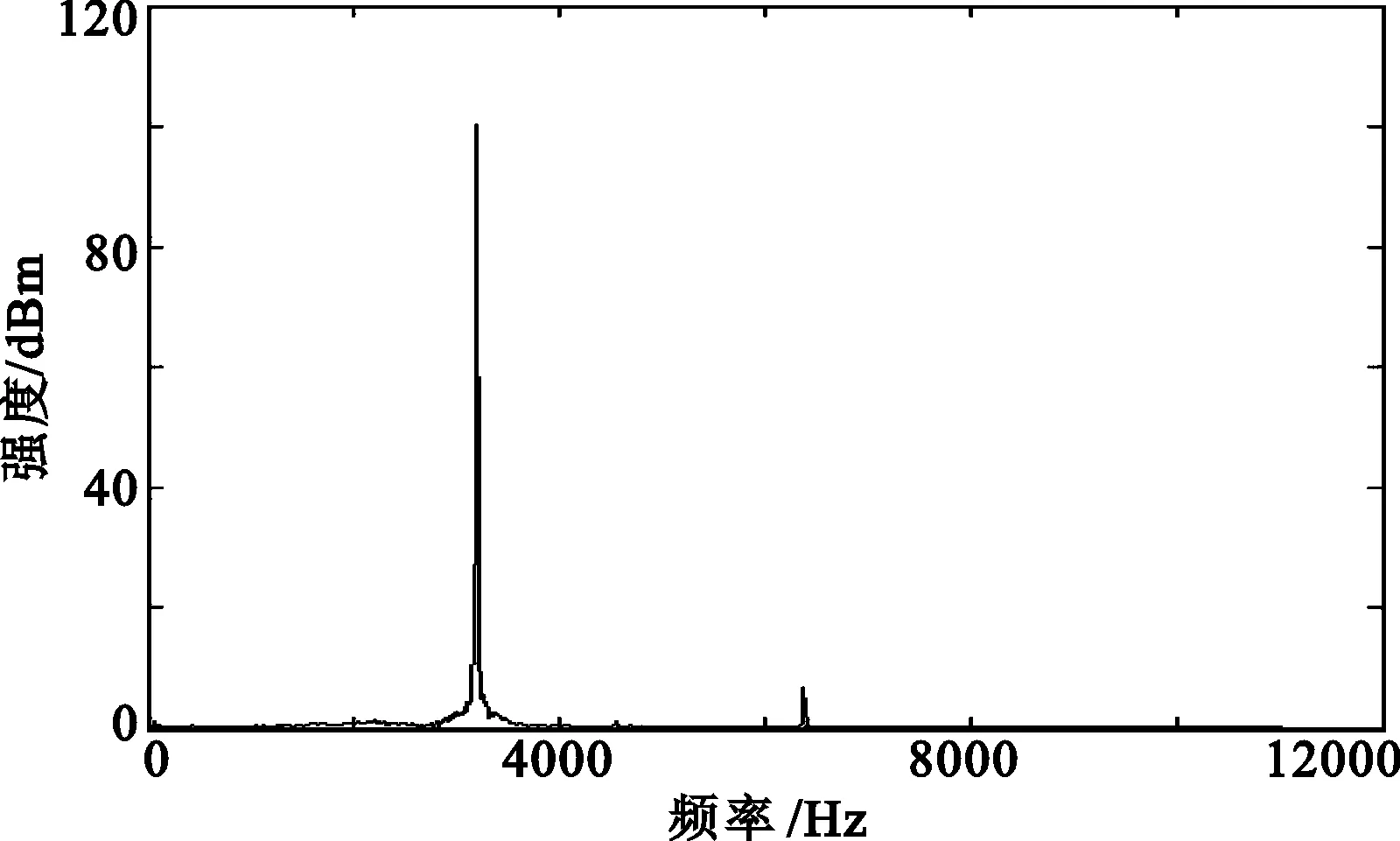
(b) 信号频谱分析

4.1.2 侧面通信

侧面通信的时域信号与单个码元信号频谱分析如图12所示。当通信设备之间无干扰且距离较近时，通信质量非常好。

(a) 通信时域

(b) 信号频谱分析

4.1.3 远距离通信

远距离(1～10 m)通信的时域信号与单个码元信号频谱分析如图13所示。由于距离较远，信号能量出现衰减，通信质量一般。

(a) 通信时域

(b) 信号频谱分析

4.1.4 固态介质通信

固态介质通信的时域信号与单个码元信号频谱分析如图14所示。由于固体也能传播声音，且受干扰少，因此当通信设备采用固态介质作为传输媒介时，通信效果较好，干扰少。

(a) 通信时域

(b) 信号频谱分析

4.1.5 遮挡下的通信

遮挡情况下通信的时域信号与单个码元信号频谱分析如图15所示。当发生遮挡时，信号能量急剧衰减，通信质量较差。

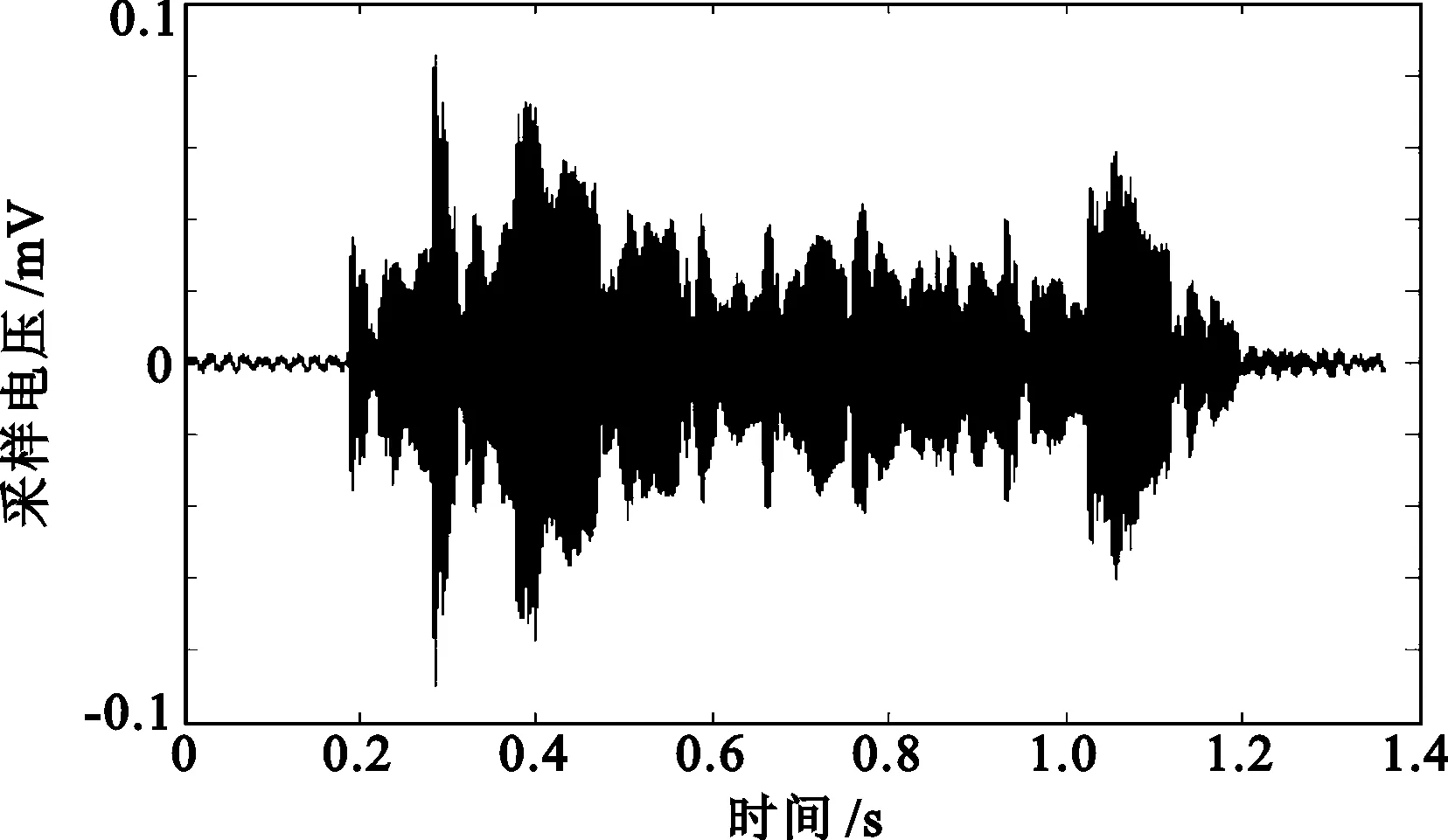
(a) 通信时域

(b) 信号频谱分析

4.1.6 统计结果

在实验环境下，进行20次通信后，所得平均信号振幅、初次识别率以及纠错后的准确率如表1所示。

表1 实验结果

实验表明，新提出的无线通信模型较为可靠，经纠错后信号准确率提高。当通信设备之间距离较近且无遮挡时，通信效果最好。在信道干扰较大的情况下，可将设备贴近墙壁，采取固态介质传播方式进行通信。

4.2 噪声干扰实验

实验采用Class A模型模拟大气噪声的干扰，以及对数正态分布模型来模拟人为噪声的干扰。

4.2.1 大气噪声干扰

对于Class A模型，采用文[17]给出的大气噪声模型进行模拟。此时时域信号与单个码元信号频谱分析如图16所示。实验表明，大气噪声的干扰对通信的影响不大。

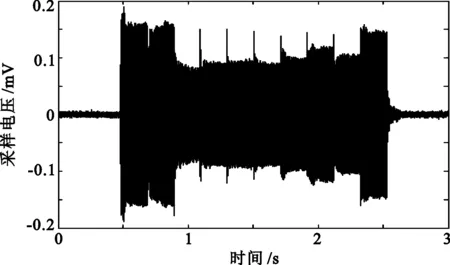
(a) 通信时域

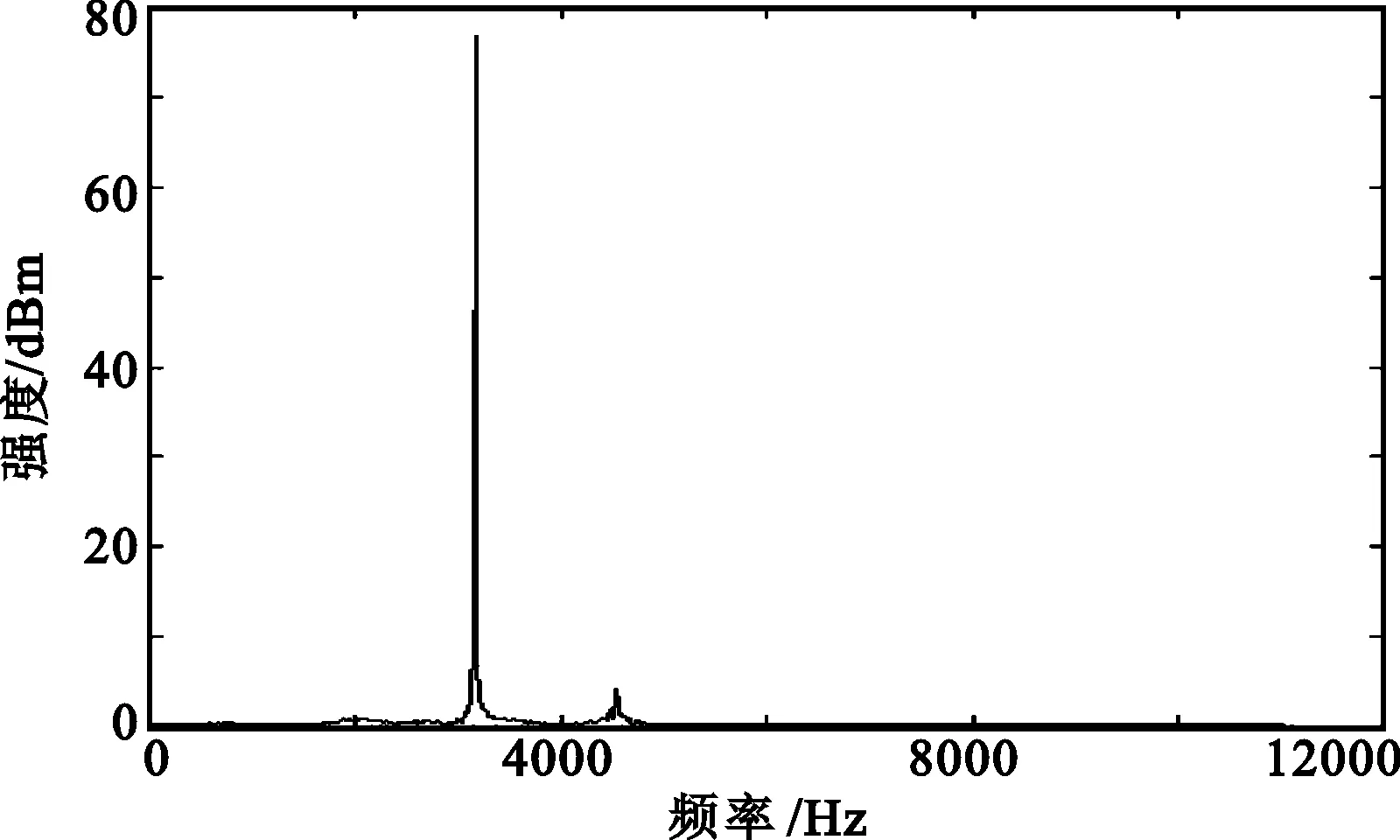
(b) 信号频谱分析

4.2.2 人为噪声干扰

因人为噪声在安静区、商业区和工业区有很大差别，因此实验采用不同强度的噪声进行干扰，如在安静区取噪声20 dB，在商业区取噪声60 dB，在工业区取噪声80 dB时的时域信号与单个码元信号频谱分析如图17所示。

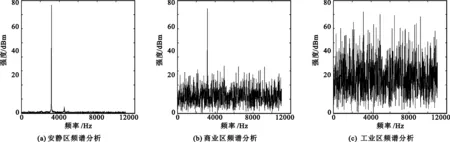
图17 人为噪声干扰

实验表明，在20dB的安静区环境下，通信传输良好。在60dB的商业区环境下，由于噪声的干扰，时域定位信息丢失，频域谐波信息丢失，但此时仍可以进行通信。在80dB的工业区环境下，时域和频域信息完全丢失，无法进行通信。

4.3 技术比较

实验采用两个Arduino作为主控制器，利用两个Bluetooth 4.0(CC2540)模块，两个WiFi模块，两个Zigbee(CC2530)模块进行对比实验。实验环境图18所示。

采用新提出的通信方法，与传统的WiFi, Bluetooth, Zigbee, RFID技术在硬件成本，通信速率，通信距离，软件复杂度上以及部署复杂度的比较结果参见表2。

(a) 实验设备

(b) 设备连接

方法硬件成本通信速率通信距离软件复杂度部署复杂度新方法1～10元258．4bps<10m直接处理数据低WiFi60～220元11Mbps<100m需了解WiFi协议栈需键入SSID以及密码Bluetooth20～100元1Mbps<10m需了解蓝牙协议栈需配对Zigbee30～200元250kbps100～1000m需了解Zigbee协议栈需配对RFID20～80元不可通信0．02～0．2m需了解标签、读写器等开发低

由表2可知，新提出的方法可以改善硬件成本高以及协议栈复杂的问题，便于在缺乏I/O交互的传感器节点上进行灵活部署。但由于通信速率以及通信距离较低，新方法不适合大量以及远距离传输。

5 结 语

利用声道进行无线通信，可改善目前物联网无线通信中高昂的硬件成本以及复杂的协议栈等问题。利用瞬态同步技术能够减少信号同步的时间和算法开销，而谐波纠错技术则可提高通信的准确率。所提出的通信模型可用于设备低速通信、设备配置、I/O交互中。

[1] 刘建华, 田岁苗, 赵勇. 基于Android的智能家居系统设计[J]. 西安邮电大学学报, 2013, 18(4):71-74.

[2] Yun Hwan Sik, Cho Kiho, Kim Nam Soo. Acoustic data transmission based on modulated complex lapped transform[J]. IEEE Signal Processing Letters, 2010, 17(1): 67-70.

[3] Sinha R, Balamuralidhar P, Bhujade R. An Upper Audio Band based Low Data Rate Communication Modem[C]//6th International Conference on Signal Processing and Communication Systems. Australia Gold Coast: IEEE, 2012: 1-8.

[4] Sinha R, Balamuralidhar P, Bhujade R. A reconfigurable upper audio band modem for data communication between mobile devices[J]. Analog Integrated Circuits and Signal Processing, 2014,78(3):669-682.

[5] Cho Namhyun, Shin Donghoon, Lee Donghyun. Performance Analysis of Noise Robust Audio Hashing in Music Identification for Entertainment Robot[J]. Information Technology Convergence Lecture Notes in Electrical Engineering, 2013, 253: 977-983.

[6] 应三丛, 张行. 基于FPGA的HDLC协议控制器[J]. 四川大学学报, 2008, 40(3): 116-120.

[7] 邬春学, 华乐. 基于 CRC 机制的信号回流检测方法与误码分析[J]. 微型机与应用, 2011, 30(21): 20-25.

[8] 林娟. 噪声环境下的说话人识别技术研究[D]. 兰州: 兰州理工大学, 2010: 1-4.

[9] 黄国庆, 靳朝, 元洪波. 基于累积量和盒维数的MFSK信号调制识别算法[J]. 郑州大学学报, 2010, 31(6): 47-50.

[10] 田宝泉, 吕鹏涛, 贺敬. 基于以太网和 PCM 的分布式机载测试系统时间延迟分析[J]. 科学技术与工程, 2013, 13(7): 2011-2014.

[11] 花小磊, 李学斌. FFT扇形衰落改善算法研究[J]. 计算机工程与设计, 2012, 33(12): 4762-4768.

[12] OguzEr Ali, Chen Jie, Tang Jau, et al. Transient lattice distortion induced by ultrashort heat pulse propagation through thin film metal/metal interface[J]. AIP Journals & Magazines, 2013, 102(5):051915.

[13] Larson R, Adducci A. Transient Distortion in Loudspeakers[J]. IRE Transactions on Audio,1961, AU-9(3):79-85.

[14] Chang Chun, Pawar S J, Weng Soar, et al. Effect of Nonlinear Stiffness on the Total Harmonic Distortion and Sound Pressure Level of a Circular Miniature Loudspeaker-Experiments and Simulations [J]. IEEE Transaction on Consumer Electronics, 2012, 58(2):212-220.

[15] 吴彦文. 移动通信技术及应用[M]. 武汉: 华中师范大学出版社, 2006: 84-89.

[16] Middleton D. Canonical and quasi-canonical probability models of Class A interference[J]. IEEE Transaction on Electromagnetic Compatibility, 1983, EMC-25(2):76-106.

[17] 蒋宇中. 超低频信道噪声统计特性及应用[D]. 武汉: 华中科技大学, 2008: 43-55.

[18] ITU. Probability distributions relevant to radiowave propagation modelling[EB/OL]. (2013-11-27)[2013-11-30]. http://www.itu.int/rec/R-REC-P.1057-3-201309-I/en.

[责任编辑:王辉]

A wireless communication model based on acoustics channel

LIU Jianhua1, ZHANG Yanbing2

(1. Information Center, Xi’an University of Posts and Telecommunications, Xi’an 710121, China;2. School of Computer Science and Technology, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

In view of the high cost of hardware and complicated protocol stack problems in Internet wireless communication in the Internet of Thing (IOT) area, a wireless communication model based on acoustics channel is proposed. In this model, Multi-Frequency Shift Keying (MFSK) is used for transmitting data on the acoustics channel. Transient Distortion Synchronization (TDS) and Harmonic Distortion Correction (HDC) are used to meet the requirements of real-time decoding with the low performance in computation. The experimental results show that compared with the existing Internet of wireless communication technology, this model is low cost at software development with deployment and good performance.

acoustics communication, wireless communication, transient distortion synchronization, harmonic distortion correction

2013-12-03

工业和信息化部软科学研究基金资助项目(2012-R-57)

刘建华(1963-)，男，正高级工程师，从事信息安全研究。E-mail:lpyljh@126.com 张雁冰(1989-)，男，硕士研究生，研究方向为计算机应用技术。E-mail:artanis@126.com

10.13682/j.issn.2095-6533.2014.02.005

TN912.11

A

2095-6533(2014)02-0030-09