基于特征结构的频谱感知算法

卢光跃， 弥 寅， 包志强， 冯景瑜

(西安邮电大学 无线网络安全技术国家工程实验室， 陕西 西安 710121)

基于特征结构的频谱感知算法

卢光跃， 弥 寅， 包志强， 冯景瑜

(西安邮电大学 无线网络安全技术国家工程实验室， 陕西 西安 710121)

为了全面认识当前的认知无线电频谱感知技术，深入研究基于特征结构的多节点合作频谱感知算法,将近年来发展的随机矩阵理论(RMT)引入到频谱感知领域，使得频谱感知性能得到提高，有可能在实际应用中实现频谱感知。通过阐述基于采样协方差矩阵及特征值类的合作频谱感知方法的基本原理，归纳其主要特点，推导出检测门限的确定方法。通过基于Matlab的仿真实验，对比和验证算法的感知性能。最后展望该方向下一步的研究趋势。

认知无线电；频谱感知；随机矩阵理论；采样协方差矩阵；特征值

随着4G时代的到来，无线设备(如：智能手机、平板电脑等)的大量普及，无线频谱资源日渐紧张，呈现出利用率不高，公共频谱拥堵，授权频谱空闲率高等特点，如何改善频谱拥堵现状，提高频谱资源利用率，从而进一步提高系统容量和通信服务质量是下一代无线通信急需解决的问题。目前的频谱资源管理方式采用固定频谱分配，它由政府机构提供授权、且只有授权用户才允许占用频带[1-2]。随着各种无线技术的快速发展，固定频谱分配不能从根本上解决频谱拥堵的问题，美国联邦通信委员会(Federal Communications Commission, FCC)研究指出，许多认知用户(Cognitive User, CU)都工作在工业、科学与医疗(Industry,Scientific,Medical,ISM)等非授权频段，而大部分授权频段却经常空闲，授权频段的频谱平均利用率仅为15%～85%。

认知无线电(Cognitive Radio, CR)[2]作为一种频谱再用技术，其基本出发点是在不对授权用户造成有害干扰的情况下，使具有认知功能的无线通信设备能够检测到、且合理地利用空闲授权频段，从而有效缓解频谱拥堵问题。FCC对于CR的定义为：认知无线电是一种能够感知其运行电磁环境的无线电或系统，能够动态、自主地调节其运行参数来改善系统的运行情况，例如最大化吞吐量、缓解干扰、促进互操作性、访问认知用户[1]。因此，CR主要的一个方面就是自主检测到空闲的频谱、并将其作为新的链路进行通信。为了实现频谱的动态“伺机”的接入，CU必须能够及时检测到授权用户(Primary User, PU)未使用的频谱(即频谱空洞)，然后调整它们的频率和其他物理层参数以有效利用这些空闲频段。

根据定义建立CR的基本认知环模型[3]。认知环模型主要包括三部分：无线资源分析(包括无线环境预测和无线频谱探测)、信道确认(包括信道状态估计和预测)、传输功率控制和动态频谱管理。其中无线资源分析实现空闲频谱的检测，是认知系统正常工作的最核心环节。然而，由于无线环境时刻变化，CR必须时刻分析频谱的空洞情况，并能够跟踪其变化，且做出相应参数调整以使系统最优。

采用动态频谱接入的CR技术现已被作为一种提高频谱利用率的解决方案[3]。当然，在发现PU要使用某空闲频段时，CU需要合理调整自身参数继续使用该频段或者转移至其他未使用的频段进行避让，以免对PU产生干扰。

事实上，在欧洲和美国的一些特定频段，监管机构正在研究CR的使用以提高频谱利用率。美国于2002年由FCC建立的频谱政策任务小组，最近颁布了关于在UHF TV波段未授权宽带无线设备的使用意见[4]。而欧洲通信委员会(European Communications Commission, ECC)正在评估470～790 MHz频带CR系统的频谱空洞使用情况[5]，从而为CR系统实施服务识别可能的候选频带。

频谱感知是实现CR的前提条件和首要任务。CU通过频谱感知，以无监督的方式来发现在特定时间、特定地理位置未被充分利用(部分或全部)的频谱子带(即频谱空洞[6])，其目的一方面为CU检测到可用的频谱资源，另一方面也限制CU对PU造成潜在干扰。因此CU采用的频谱感知方法的检测性能将直接影响整个CR网络的性能。

1 频谱感知算法简述

目前，众多的频谱感知算法按不同的分类标准，可以得到不同的分类结果。根据认知用户所处的感知位置，可分为主用户发射机检测和主用户接收机检测；根据参与感知的节点数的不同，可分为单节点感知[7-9]和多节点合作感知[10-13]；根据是否需要先验信息，可分为非盲感知和盲感知；根据是否需要汇聚节点，可分为中心式感知[14]和分布式感知[15]；根据数据融合方式，可分为硬合并[16-18]、软合并[19-20]和双门限[21-23]。本文正是根据这些分类标准对频谱感知技术的研究现状进行了归纳总结，对备受关注的基于特征值[24-31]和协方差矩阵[32-36]的检测算法进行了较为详细的阐述。算法分类如图1所示。

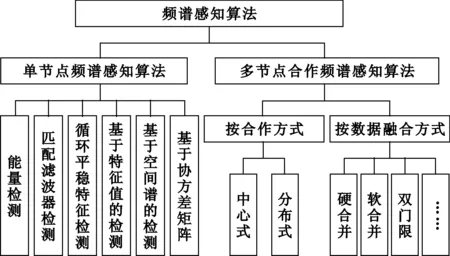
图1 频谱感知算法分类

在单节点检测方面，经典的频谱感知算法[7]有匹配滤波器检测、能量检测(Energy Detection, ED)、循环平稳特征检测等。其中匹配滤波器检测[8,37-38]在加性高斯白噪声环境下性能最优，但其同步要求较高，且必须预知PU发射机信号的先验知识(如信号波形、调制方式等)，限制了算法的应用范围；最常用的能量检测[9,39]不需要知道PU发射机信号的任何先验知识，实现简单，但受噪声不确定度,即信噪比(Signal to Noise Ratio, SNR)门限影响大，门限设置困难[40]；循环平稳特征检测算法[41-43]利用通信信号本身具有的循环周期特性来检测授权用户的存在性，不需要预知授权用户信号的先验知识，检测性能较好，缺点是计算较复杂，需要更长的检测时间，降低了系统的灵敏度。

针对以上的单节点频谱感知算法存在的问题，学者们对接收信号的采样协方差矩阵的分布特性做了大量深入的研究。在不同的检测算法中，有不同的检测门限确定方法。文献[44-47]对Wishart矩阵的特征根进行了分析，根据大维RMT理论，研究者提出了LSC算法[24]，它将最大最小特征值之比作为检验统计量，采用渐近理论，门限直接采用特征值的渐近值获得，但其感知性能在采样数较小时不够理想。因此，MME算法[25-26]被提出来，它同样采用最大最小特征值之比做为检测统计量，研究并分析了最大特征值的极限分布，结合最小特征值的渐近值，从而推导出给定虚警概率条件下的判决门限，它充分考虑了实际中采样数较小的问题，这属于半渐近的理论。

DMM算法[27]是西安邮电大学通信信号处理研究团队较早提出的一种盲感知方法，该方法利用最大最小特征值之差作为检验统计量，使用最大特征值的极限分布，通过估计噪声对判决门限实时更新，其检测性能明显优于ED算法，并能有效克服噪声不确定度的影响，是一种稳健的盲感知算法。为了提高检测性能，在DMM算法的基础上，根据最新的RMT理论，我们后续又提出了NDMM合作感知算法[28]，检验统计量不变，对门限的确定方法进行了改进。

可以看出，基于特征值的频谱感知方法有很好的感知效果，但也有两个严重的缺点。第一：RMT被用于近似实际的累积分布函数，这样得到的判决门限并不准确，而是渐近的，因此在采样快拍数较少时，真实与理论的判决门限误差较大。第二：这类算法都需要进行特征值分解，计算复杂度较高，不利于实时信号处理。为了解决这些问题，学者提出了基于协方差绝对值的频谱感知方法(CAV)[33]，它不需要对协方差矩阵进行特征值分解，大大减少了计算复杂度，但和其他基于特征值的感知算法一样，在求判决门限时都需要做渐近假设。为了解决判决门限非渐近假设的问题，Yang提出了基于协方差矩阵的Clolesky分解感知方法(CDC)[34]，但是需要对样本协方差矩阵做Clolesky分解，运算量仍然较大。

为此，西安邮电大学通信信号处理研究团队又研究了小样本环境下的快速盲频谱感知方法，即基于最大相关系数(MCC)[35]和基于多重相关系数(CMC)[36]的盲频谱感知方法，这两种方法的判决门限是非渐进的，计算复杂度较小，在小样本环境下的感知性能较好。

2 检测算法模型及理论

基于采样协方差矩阵特征结构的频谱感知算法的主要思想是充分利用PU信号与白噪声不同的相关性进行的。PU信号经过多径衰落、多天线接收或过采样后通常都具有相关性，而这种相关性可用来判定PU信号存在与否。

通常，频谱感知可以表述为一个二元假设检验问题[48]，即存在两种假设：H0表示主用户不存在，频段空闲，认知用户可接入该频段；H1表示主用户存在，频段被占用，认知用户不可接入该频段。因此，频谱感知的数学模型为

其中xi(n)表示第i个CU在第n个时刻采样到的信号向量；s(n)表示PU发射机信号经过路径损失和多径衰落后被第i个CU接收到的信号向量；ηi(n)表示均值为0、方差为σ2的独立同分布加性高斯白噪声向量。

通常情况下，频谱感知方法检测性能常用以下评价指标。

(1)虚警概率(Pfa) :没有授权用户但检测结果为存在授权用户信号的概率。虚警的发生会将空闲频谱资源误判为被占用的频谱资源，因此将降低系统整体的频谱效率。

(2)检测概率(Pd):授权用户信号存在并正确检测到此信号的概率。

(3)漏警概率(Pm):与检测概率相对应，定义为

Pm= 1 -Pd。

漏警的发生会将占用的频谱资源误判为空闲频谱资源，因此一旦CR使用该段频谱，就会造成对主用户的干扰。

一般情况下，频谱感知算法性能的衡量是通过在给定系统要求的Pfa约束条件下，分析感知算法所能达到的检测概率Pd的大小。Pfa一定时，Pd越大，算法的性能越好。

然而，考虑感知算法在实际系统中应用，还需要考虑算法的实用性(如实时性、硬件实现的复杂程度等)。同时，感知算法检测性能很大程度上还会受到信道条件(如路径损失、多径、衰落、本地干扰和噪声不确定度等)的影响。

M个认知用户对PU发射机信号采样得到的信号构成一个向量

X=[x1,x2, …,xM]T，

同理可得

S=[s,s, …,s]T，

η=[η1,η2, …,ηM]T,

其中xi(i=1,2,…,M)表示第i个认知用户采样N次得到的信号向量。因此，X可以用一个M×N维的矩阵表示为

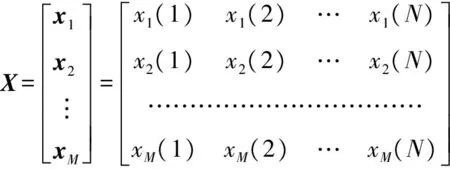
假设S与η相互独立，H1成立时，考虑M个认知用户接收信号的采样协方差矩阵

Rx=E[XXH]，

经过信道后的PU信号的统计协方差矩阵

Rs=E[SSH]，

那么

Rx=Rs+σ2IM。

实际情况中，由于无法准确计算Rx，所以只能采用有限采样来估计协方差矩阵[45]，即

(1)

其中H表示共轭转置变换。

假设H0成立时，s(n)不存在，即Rs=0，则

Rx=σ2IM；

当H1成立时，Rs≠0。令Rx的最大最小特征值分别为λmax和λmin，Rs的最大最小特征值分别为ρmax和ρmin，容易得出

λmax=ρmax+σ2，λmin=ρmin+σ2，

显然，当H0成立时, 有

λmax=λmin=σ2，

当H1成立时,有

λmax>σ2=λmin。

也就是说，H0和H1两种情形时，Rx特征值分布的差异为频谱感知提供了一条解决思路。

近年来，最新的RMT理论不断被应用到频谱感知领域[21-22,24-28,30-31,49]。当H0成立时，Rx(N)为特殊的Wishart随机矩阵[50]。文献[44]对Wishart 随机矩阵的特征根进行了研究。文献[45-46]分析了噪声为实信号和复信号的情形下，Wishart随机矩阵最大特征值服从Tracy-Widom分布F1(t)。当N足够大时，两种情形下最大特征值的均值和方差几乎一样，但其极限分布不同。在文献[47]中，Penna等人发现在当M、N→∞时，其最小特征值也服从Tracy-Widom分布。

定理1(M-P律)[44]设M×N随机矩阵W中的元素满足零均值独立同分布(实数或复数)，方差为σ2/N，则当M、N→∞且α=M/N时，WWH的经验分布几乎一定收敛到一个非随机极限分布，即M-P律[45]，它的概率密度函数为

(2)

其中

分别为最小特征值和最大特征值的渐近值，即λ∈[a,b]，而σ2为方差，δ(x)为单位冲击函数，(a)+为a和0中取大者。

定理2[45-46]当噪声为实信号时，令

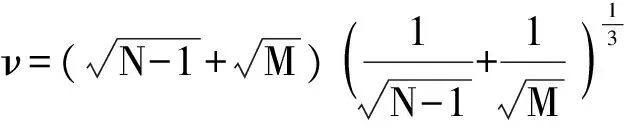
并假设

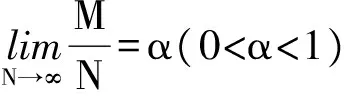
定理3[47]当噪声为实信号时，令

并假设

。

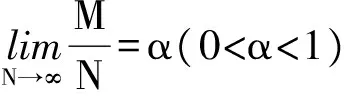
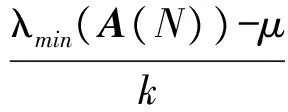
3 特征值类的检测算法

特征值类算法均按以下步骤进行。

步骤1 进行数据采样，并根据式(1)估计接收信号采样协方差矩阵Rx(N)。

步骤2 对Rx(N)进行特征值分解，求得λmax和λmin，进而得出检验统计量T。

步骤3 根据系统要求的虚警概率，利用定理1、定理2和定理3，计算判决门限γ。

步骤4 按规则判决，即当T≤γ时，选取假设H0,否则，选取假设H1。

不同的算法区别主要在于其检验统计量的构造方式不同，以及其判决门限确定方法的不同。

3.1LSC算法

因为采样协方差矩阵的最大特征值和最小特征值包含了信号和噪声的信息，它们的比值则反应了信号和噪声强度之比，而PU信号存在与否将会影响最大最小特征值的分布。因此，利用这一特性，根据在两种假设检验情况下λmax/λmin的不同，利用λmax/λmin作为检验统计量来判决PU信号是否存在。

LSC算法是一种基于RMT的渐进算法。在频谱感知中，假设噪声为零均值独立同分布，信号与噪声不相关。当N较大时，采样协方差矩阵近似等于统计协方差矩阵，而统计协方差矩阵可视为是大维随机矩阵

在H0时，采样协方差矩阵为特殊的Wishart随机矩阵，依据定理1(M-P律)，可以得出最大的渐近值b和最小特征值的渐近值a。在H1时，信号服从spiked population models，此时根据其大维随机矩阵最大特征根分布原理，主用户的存在使其最大特征根的渐近值b′大于b。

根据H0和H1时采样协方差矩阵最大特征值渐近值的不同，可以区分PU用户存在与否。因此，LSC算法即是采用采样协方差矩阵特征值的渐近值之比作为检测统计量，其判决门限为

(3)

LSC算法相较于ED算法，有了很大改进，不需要预知PU发射机信号，同时能很好的克服实际环境中的噪声不确定影响，但在实际应用小采样的情形下性能不够理想。

3.2 MME/DMM算法

3.2.1 MME算法

MME(Maximum-minimum Eigenvalue Detection)算法主要依据的是H0和H1时最大最小特征值的差别。事实上，理想情况下，当H0成立时,有

λmax=λmin=σ2，

而当H1成立时,有

λmax>σ2=λmin,

因此MME算法的检验统计量为最大最小特征值之比，即

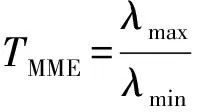
理想情况下MME算法的判决门限为1，但由于λmax与λmin只有借助于Rx(N)才能得到，而Rx(N)只是Rx的估计，因此TMME的实际门限与理想门限会有偏差。为此推导其检测门限。

检测门限的确定通过分析H0时Wishart随机矩阵Rx(N)的最小特征值极限值及最大特征值的极限分布得到。由M-P律可得到最小特征值的极限值，即当M、N→∞，有

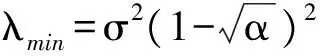
可由定理3知协方差矩阵最大特征值的极限分布。

为此，建立H0时判决门限γMME与虚警概率Pfa之间的关系

Pfa=P{λmax>γMMEλmin|H0}=

P{λmax[A(N)]>γMMEa}。

(4)

当噪声为实信号时，推导得MME算法的判决门限

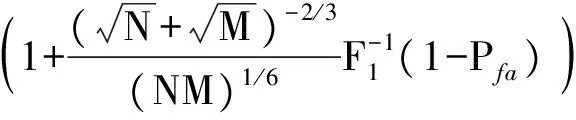
(5)

假设PU发送信号为QPSK调制信号，设

Pfa=0.1，

每次仿真基于10 000次的蒙特卡洛计算，认知用户数为10，采样次数为3 200，噪声的方差为1，以“ED-xdB”表示有噪声不确定度的ED算法。估计的噪声方差为

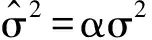
设噪声不确定度为

B=max{10 lgα}，

其中α(dB)在[-B,B]上服从均匀分布。ED算法噪声不确定度为0 dB、1 dB和2 dB，MME算法噪声不确定度为1 dB。图2给出LSC、MME与ED算法的检测概率Pd性能曲线比较。

由图2可见，当信噪比RSN=-20 dB时，ED-1dB和ED-2dB检测概率分别仅为5%和4%，而LSC的检测概率可达28%，MME算法甚至达到65%。LSC算法虽然相比ED算法已经有了很大改进，但小采样时性能还不够理想，MME更加适合小采样的实际情况；同时，LSC和MME算法均不受噪声不确定度影响，检测性能更加稳健和优越。

图2 LSC、MME与ED算法检测性能对比

3.2.2DMM算法

MME算法主要依据的也是H0和H1时最大最小特征值的差别。事实上，理想情况下，在H0时，所有特征根相同，最大最小特征值之差为0；而H1时，最大最小特征值将大于0(大于零的程度取决于其信噪比的大小)。因此，DMM(DifferencebetweentheMaximumEigenvalueandtheMinimumEigenvalue)算法设计的检验统计量为最大最小特征值之差，即

TDMM=λmax-λmin。

可见，理想情况下DMM算法的判决门限为0，但由于λmax与λmin只有借助于Rx(N)才能得到，而Rx(N)只是Rx的估计，因此TDMM的实际门限与理想门限会有偏差。为此推导其判决门限。

基于定理1(M-P律)及定理2，若信号为实信号，Pfa可以表示为

Pfa=P{λmax-λmin>γDMM|H0}=

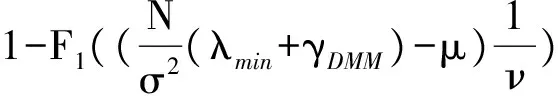
(6)

化简得DMM检测算法的判决门限

(7)

推导式(7)时λmin采用的是M、N→∞的极限值,然而,实际感知时N是有限的，因此会造成门限的偏差。为尽量降低利用λmin估计噪声能量时带来的误差，估计噪声方差为

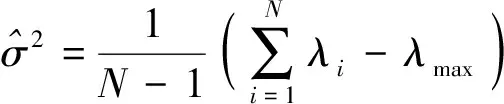
(8)

假设PU发送信号为QPSK调制信号，每次仿真基于10 000次的蒙特卡洛计算，认知用户数为4或8，采样次数为320，噪声方差为1或10，噪声不确定度为0 dB或1 dB。图3给出的是DMM与ED算法的检测性能曲线。

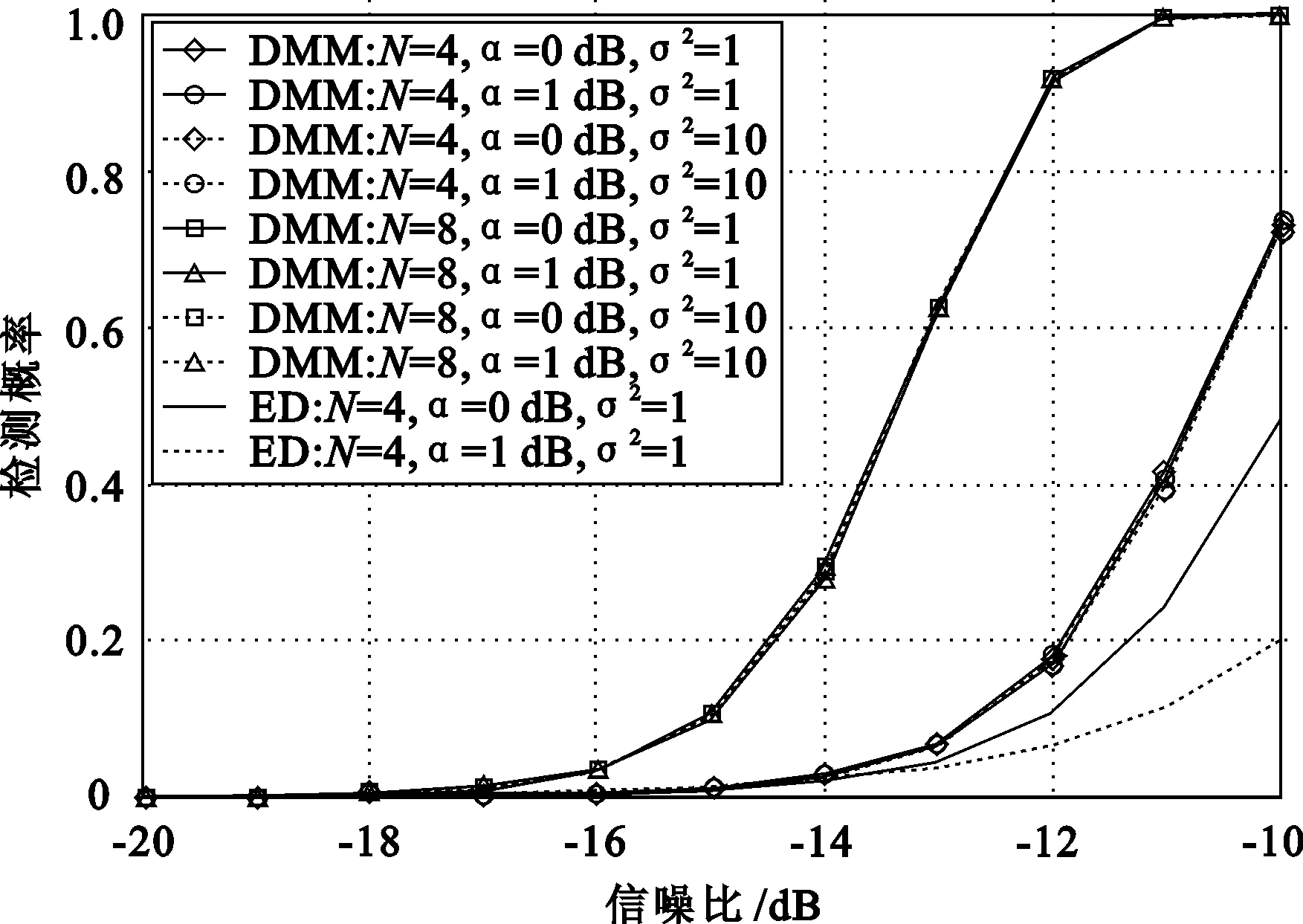
图3 DMM与ED算法检测性能对比

可见，ED算法受噪声不确定度影响大，而DMM算法通过估计噪声方差，实时更新门限，不受噪声方差和噪声不确定度的影响。随着认知用户数的增加，算法的检测性能得到提高，当信噪比RSN=-12dB时，DMM算法的检测概率从18%提高到90%，性能明显优于ED检测算法。

3.3NDMM算法

随着RMT的发展，人们发现当M、N→∞时，Wishart随机矩阵的最小特征值也服从Tracy-Widom分布[44]，即定理3。而且采用最小特征值的极限分布进行门限确定时，比目前所采用的最大特征值的极限分布函数更精确[31,47]，因此在确定判决门限时，使用λmax的极限值近似代替λmax，从而得出新的门限判决方法。

NDMM算法的判决统计量同DMM算法一致，应用定理1和定理3，采用最小特征值的极限分布，利用最大特征值的极限值。假设噪声为实信号，则虚警概率Pfa可表示为

Pfa=P{λmax-λmin>γNDMM|H0}=

(9)

化简得

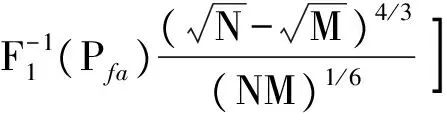
(10)

对于复信号，阈值中的不同仅在于用函数F2代替F1。

假设PU发送信号为QPSK调制信号，且

Pfa=0.1，

每次仿真基于10 000次的蒙特卡洛计算，认知用户数为5，采样次数为6 400或9 600，ED算法噪声不确定度为0 dB、0.5 dB和1 dB，DMM、NDMM算法噪声不确定度为1 dB。图4给出的是DMM、NDMM与ED算法的检测性能曲线比较。

图4 DMM、NDMM与ED算法检测性能对比

由图4可知，当N=6 400，RSN=-18dB时，DMM算法的检测概率为60%，而NDMM算法能达到98%，通过估计噪声克服了噪声方差的影响，在给定虚警概率的条件下，相比于DMM算法有着更高的检测概率，性能也更为稳健。

4 基于协方差矩阵的检测算法

基于特征值类的算法需要对采样协方差矩阵进行特征值分解，其计算量大，因此，研究者也考虑直接采用采样协方差矩阵进行频谱感知[32-36]。事实上，根据前文模型分析可知，如果s(n)不存在，Rs=0，则Rx的非对角元素都为0；如果PU信号存在且信号采样相关，Rs就不是一个对角矩阵，则Rx有部分的非对角元素是非零的。相应地，协方差矩阵类算法的步骤可描述如下。

步骤1 进行数据采样，并根据式(1)估计接收信号采样协方差矩阵Rx(N)。

步骤2 直接对Rx(N)矩阵内元素进行操作，进而得出检验统计量T。

步骤3 根据系统预设的虚警概率Pfa，计算判决门限 γ。

步骤4 按规则判决，即当T≤γ时，选取假设H0,否则，选取假设H1。

不同的协方差矩阵类算法区别主要在于其检验统计量的构造方式不同，以及其判决门限确定方法的不同。

4.1CAV算法

基于采样协方差矩阵绝对值算法(CovarianceAbosuteValue,CAV)正是利用PU信号有无时其协方差矩阵的差异来检测PU信号是否存在。

不妨令

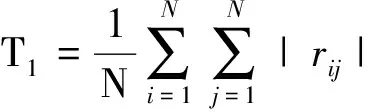
其中rij是Rx(N)的第i行、第j列的元素，可见，T1为Rx(N)所有元素绝对值之和除以N，而T2为Rx(N)对角线元素绝对值的平均值。CAV算法的检验统计量设计为

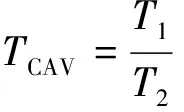
令判决门限为γCAV，如果TCAV>γCAV，则PU信号存在；否则，PU信号不存在。

由文献[32]知

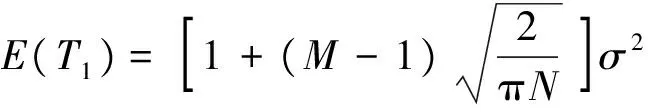
根据中心极限定理，T2近似服从高斯分布。在H0下，建立判决门限与虚警概率之间的关系

(11)

其中

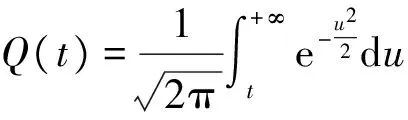
故判决门限为

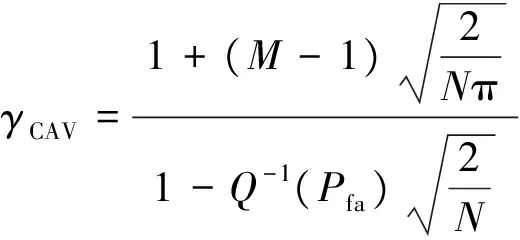
(12)

CAV算法在求取检验统计量时，直接利用接收信号采样协方差矩阵的数据元素，不需要进行特征值分解，因此相较于特征值类算法而言，CAV算法大大降低了算法复杂度，更利于硬件方面的实现，其性能与MME算法相似，而且同样无需知道授权信号、无线信道及噪声方差的先验知识，克服噪声不确定度的影响。

4.2 CDC算法

CDC检测算法的检测统计量可以定义为

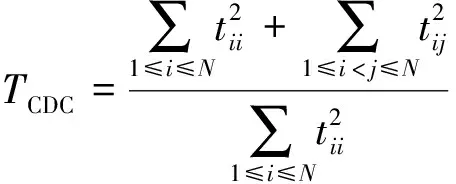
(13)

其中tij是对Rx(N)进行Cholsky分解

Rx(N) =LLH

后得到的上三角阵L的第i行、第j列的元素。应用已知结论

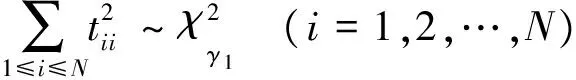
(14)

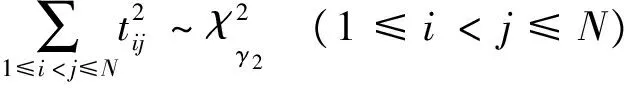
(15)

其中

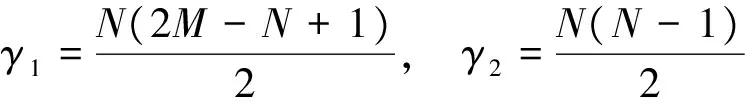
式(14)和式(15)是统计独立的两个和，结合贝塔分布的定义

可定义TCDC的累积分布函数为

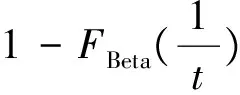
(16)

在虚警概率Pfa给定的情况下，有

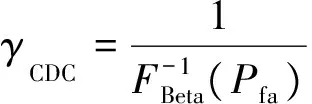
(17)

4.3 MCC算法

接收端M个阵元在N次采样中接收到的信号是相互统计独立的。依据中心极限定理，有

X(n)～N(μ,Σ)。

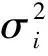
(18)

ρij的极大似然估计是

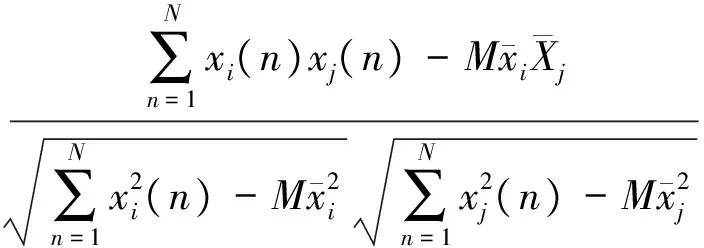
(19)

其中xi(n)是X(n)的第i个分量且

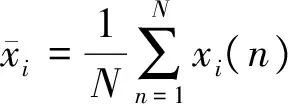
如果所观测的频段内没有主用户信号，即xi(n)和xj(n)的总体相关系数为0，我们需要知道此时ρij的分布。如果ρij=0，则ρij的概率密度是

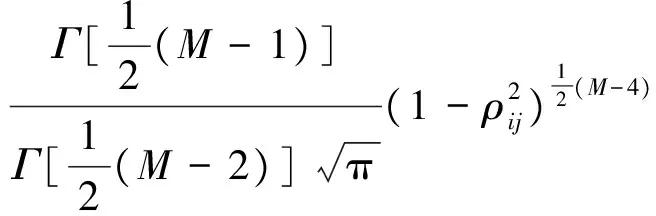
(20)

构造检验统计量

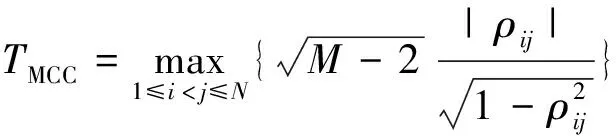
(21)

则检验统计量的概率密度函数为

(22)

在频段空闲，仅有噪声的情况下，总体相关系数ρij=0，所以检验统计量TMCC接近于0。在有信号的情况下，TMCC≠0。由于

Pfa=1-FTMCC(γMCC)=1-Fn(γMCC),

(23)

经过整理，给定虚警概率可得判决门限

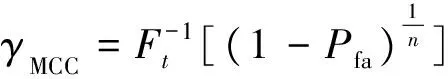
(24)

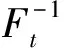
图5所示为MCC、CAV、MME、MET、CDC检测性能随信噪比变化曲线比较，所给的虚警概率为Pfa=0.1，采样数分别为40。

图5 检测性能随信噪比变化曲线对比

从图5中可以清楚的看到，所提的MCC算法曲线比MET、MME、CAV、CDC的检测效果均要好。MCC在采样数较小的情况下，表现出了比CDC算法明显良好的检测性能。而且CDC算法还要计算协方差矩阵以及进行Cholesky分解，但MCC算法计算复杂度要小很多。

图6是 ROC性能曲线比较，可以看出，在低采样数的情况下，MCC算法表现出了比CAV、MME、MET、CDC更加良好的ROC性能。

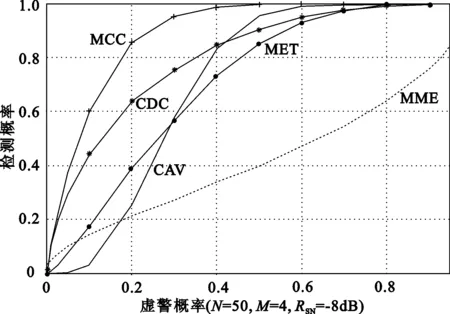
图6 ROC性能曲线对比

4.4 CMC算法

给定样本X(1),X(2),…,X(N)，并设

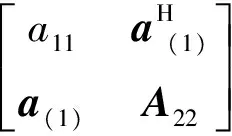
则样本多重相关系数定义为

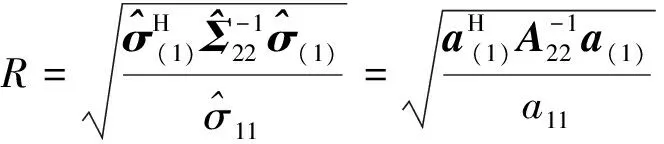
(25)

如果没有主用户信号，则

又因为R≥0，则备择假设是R>0。所以我们的问题可以归纳为二元假设检验

H0：R=0，H1：R>0，

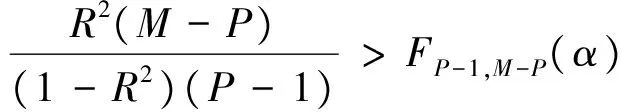
(26)

其中FP-1,M-P(α)是相应于显著性水平α的(上)分位数。

图7所示为CMC、CAV、MME、MET、CDC检测性能随信噪比变化曲线比较，所给的虚警概率为Pfa=0.1，采样数分别为40。

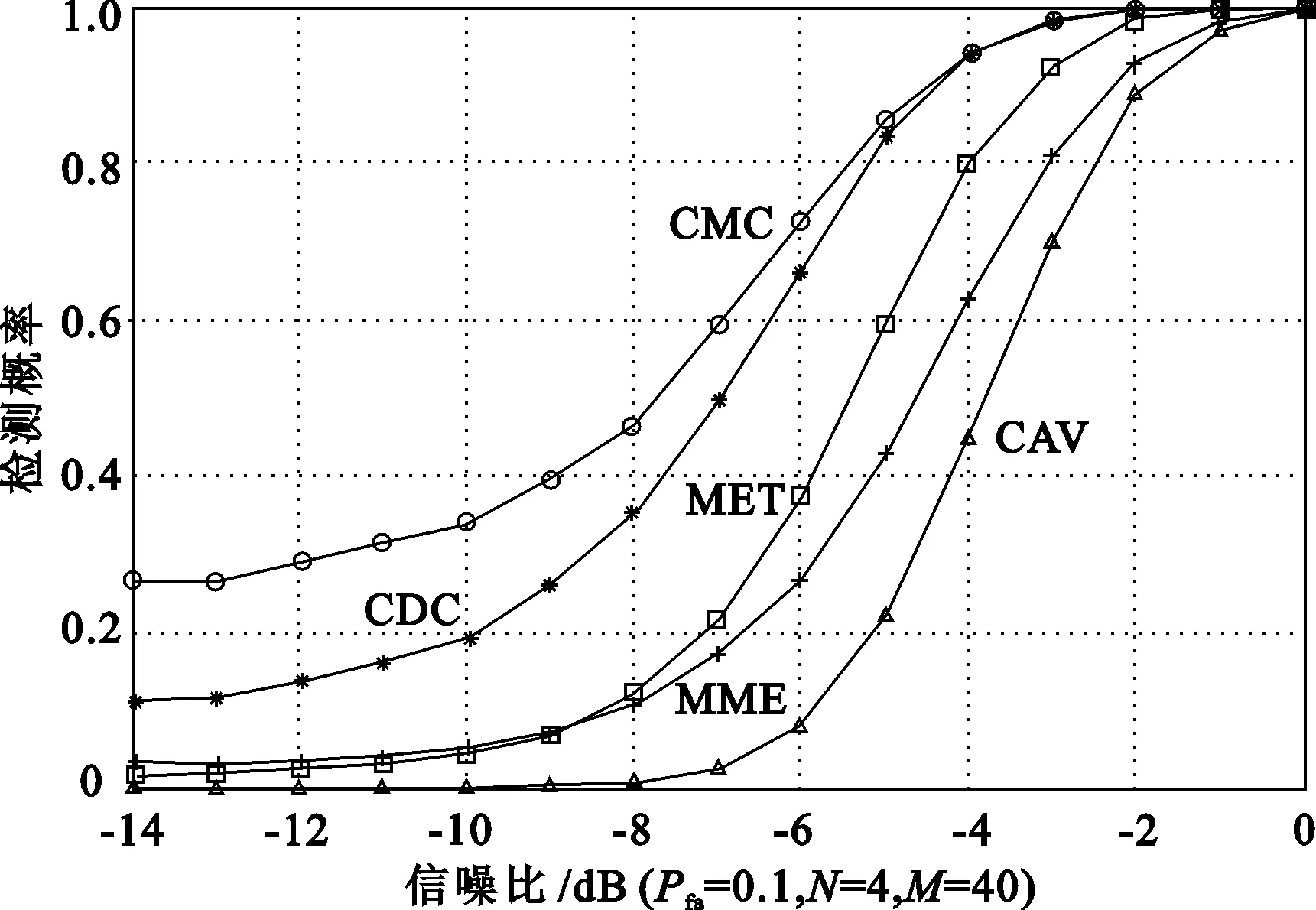
图7 检测性能随信噪比变化曲线比较

从图7中可以清楚的看到，所提的CMC算法曲线比MET、MME、CAV、CDC的检测效果均要好。由图8给出不同算法的ROC性能曲线比较，可见，在低的采样数的情况下，CMC算法表现出了比CAV、MME、MET和CDC更加良好的ROC性能。

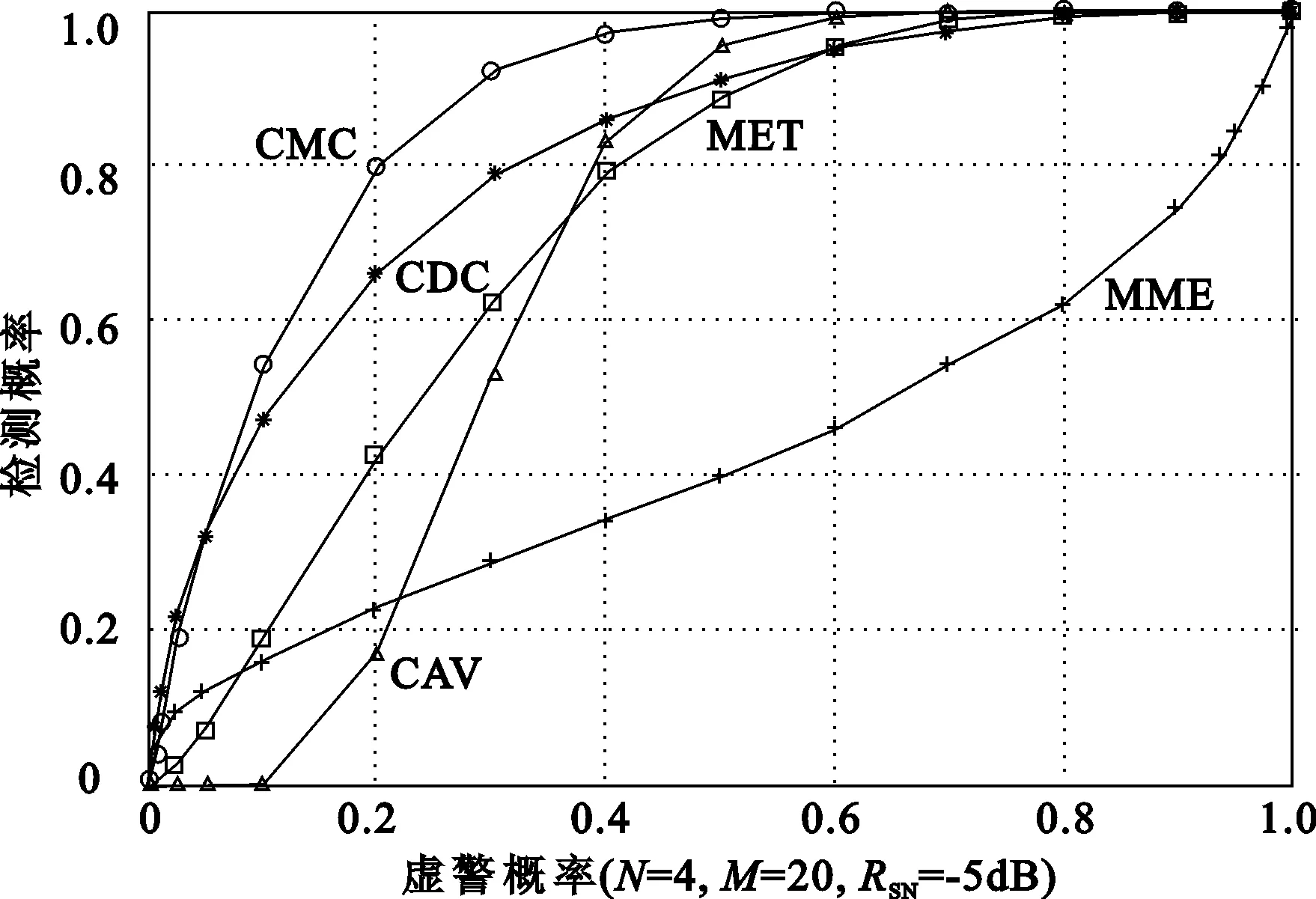
图8 ROC性能曲线比较

5 结论和展望

随着RMT理论的发展，渐近与半渐近理论的应用使得频谱感知性能得到提升。基于特征结构的多节点合作频谱感知提高了检测概率，减少了对感知设备的灵敏度要求。通过对协方差矩阵的特征根研究发现，不仅可以采用最大特征值的极限分布确定门限，如经典的MME、DMM算法，而且最小特征值也可以用来确定判决门限，其分布函数更为精确，新提出的算法性能更优越。而且，RMT的非渐近理论适合更加实际的情况，有望在以后的工作中进一步展开研究。基于特征值算法的感知性能通过增加复杂度而获得性能的提升，而基于协方差矩阵特征矢量的算法能极大地降低算法复杂度，且在采样快拍数较少时，其性能优于基于特征值的感知方法。

考虑到多个认知用户协作进行频谱感知时，会存在恶意用户，从而造成检测性能下降，因此对频谱感知中存在恶意节点的探测将有待进一步研究。再者，集中式算法对融合中心节点的依赖过高，分布式算法可以弥补这一缺点，从而提高网络的稳健性。因此，围绕非信任环境及分布式环境下基于特征值结构的频谱感知算法也是将来研究的关键点。此外，本文上述方法是基于特征值进行的，实际上从特征矢量上也可以清晰有效地区分信号和噪声，这也是目前进行频谱感知研究的另一个重点。

[1] 宋志群,刘玉涛,王荆宁.认知无线电技术及其应用[M].北京:国防工业出版社,2012:1-10.

[2] Akyildiz I F, Lee W Y, Chowdhury K R. CRAHNs: Cognitive Radio Ad Hoc Networks[J]. Ad Hoc Networks, 2009, 7(5):810-836.

[3] De Vito L. A Review of Wideband Spectrum Sensing Methods for Cognitive Radios[C]//Instrumentation and Measurement Technology Conference.Austria Graz: IEEE International,2012:2257-2262.

[4] Federal Communications Commission. In the Matter of Unlicensed Operation in the TV Broadcast Bands: Second Memorandum Opinion and Order: Report of Federal Communications Commission[R]. Washington:FCC, 2010.

[5] Electronic Communications Committee. Technical and Operational Requirements for the Possible Operation of Cognitive Radio Systems in the White Spaces of the Frequency Band 470-790MHz: Report of Electronic Communications Committee[R]. Copenhagen:ECC, 2011.

[6] Haykin S, Thomson D J, Reed J H. Spectrum Sensing for Cognitive Radio[J]. Proceedings of the IEEE,2009, 97(5):849-877.

[7] Yucek T, Arslan H. A Survey of Spectrum Sensing Algorithms for Cognitive Radio Applications[J]. IEEE Communications Surveys and Tutorials,2009,11(1): 116-130.

[8] Cabric D, Mishra S M, Brodersen R W. Implementation Issues in Spectrum Sensing for Cognitive Radios[C]//Conference Record of the 38th Asilomar Conference on Signals, System, and Computers, CA Monterey: IEEE, 2004: 772-776.

[9] Digham F F,Alouini M S.On the Energy Detection of Unknown Signals Over Fading Channels[J].IEEE Transactions on Communications,2007,55(1):21-24.

[10] Cabric D, Tkachenko A, Brodersen R W. Experimental Study of Spectrum Sensing Based on Energy Detection and Network Cooperation[C]//Proceedings of The First International Workshop on Technology and Policy for Accessing Spectrum,NewYork,USA:ACM, 2006.

[11] Ghasemi A, Sousa E S. Collaborative Spectrum Sensing for Opportunistic Access in Fading Environments[C]//2005 First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks. USA VA Mclean：IEEE DySPAN, 2005:131-136.

[12] Mishra S M, Sahai A, Brodersen R W. Cooperative Sensing Among Cognitive Radios[C]//IEEE International Conference on Communications.Turkey Istanbul：IEEE, 2006:1658-1663.

[13] Visotsky E, Kuffner S, Peterson R. On Collaborative Detection of TV Transmissions in Support of Dynamic Spectrum Sharing[C]//2005 First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks. USA VA Mclean：IEEE DySPAN, 2005:338-345.

[14] Pratas N, Marchetti N, Prasad N R. Centralized Cooperative Spectrum Sensing for Ad-hoc Disaster Relief Network Clusters[C]//2010 IEEE 71st Vehicular Technology Conference. Taibei:IEEE,2010:1-5.

[15] Pratas N, Marchetti N, Prasad N R. Decentralized Cooperative Spectrum Sensing for Ad-hoc Disaster Relief Network Clusters[C]//2010 IEEE 71st Vehicular Technology Conference. Taibei: IEEE, 2010:1-5.

[16] Pratas N, Marchetti N, Prasad N R, et al. Adaptive Counting Rule for Cooperative Spectrum Sensing Under Correlated Environments[J]. Wireless Personal Communications,2012,64(1):93-106.

[17] Edward Chu Yeow Peh , Liang Ying-Chang, Guan Yongliang, et al. Optimization of Cooperative Sensing in Cognitive Radio Networks:A Sensing-Throughput Tradeoff View[J]. IEEE Transactions on Vehicular Technology, 2009,58(9): 5294-5299.

[18] Wang Xiaofan, Chen Guangrong. Complex Networks:Small-World,Scale-Free and Beyond[J]. IEEE Circuits and Systems Magazine,2003,3(1):6-20.

[19] Ma Jun, Zhao Guodong, Li Ye. Soft Combination and Detection for Cooperative Spectrum Sensing in Cognitive Radio Networks[J]. IEEE Transactions on Wireless Communications,2008,7(11):4502-4507.

[20] Quan Zhi, Cui Shuguang, Sayed A H. Optimal Linear Cooperation for Spectrum Sensing in Cognitive Radio Networks[J]. IEEE Journal of Selected Topics in Signal Processing,2008,2(1):28-40.

[21] 邹卫霞, 丁奇, 周正. 基于特征值极限分布的双门限频谱感知算法[J].系统工程与电子技术,2012,34(3):588-591.

[22] 曹开田, 杨震. 基于随机矩阵理论的DET合作频谱感知算法[J]. 电子与信息学报,2010,32(1):129-134.

[23] 张亮, 冯景瑜, 卢光跃. 协作频谱感知中的可信双门限硬判决融合算法[J].信号处理,2014,30(2): 181-188.

[24] Cardoso L S, Debbah M, Bianchi P, et al. Cooperative Spectrum Sensing Using Random Matrix Theory[C]//3rd International Symposium on Wireless Pervasive Computing. Luxembourg:IEEE,2008:334-338.

[25] Zeng Yonghong, Liang Yingchang. Maximum-minimum Eigenvalue Detection for Cognitive Radio[C]//The 18th Annual IEEE International Symposium on Personal,Indoor and Mobile Radio Communications. Athens:IEEE,2007:1-5.

[26] 杨晓妮,卢光跃.基于特征概比分布的协作频谱感知算法研究[J].西安邮电学院学报, 2010,15(5):5-8.

[27] 王颖喜, 卢光跃. 基于最大最小特征值之差的频谱感知技术研究[J].电子与信息学报,2010,32(11):2572-2574.

[28] 卢光跃, 弥寅, 包志强. 特征值极限分布的改进合作频谱感知[J]. 信号处理, 2014,30(3):261-267.

[29] Letaief K, Zhang Wei. Cooperative Communications for Cognitive Radio Networks[J]. Proceedings of the IEEE,2009,97(5):878-893.

[30] Zeng Yonghong, Koh C L, Liang Yingchang. Maximum Eigenvalue Detection:Theory and Application[C]//IEEE International Conference on Communications, Beijing:IEEE,2008:4160-4164.

[31] 曹开田, 杨震. 基于最小特征值的合作频谱感知新算法[J]. 仪器仪表学报,2011,32(4):736-741.

[32] Zeng Yonghong, Liang Yingchang. Spectrum-Sensing Algorithms for Cognitive Radio Based on Statistical Covariances[J]. IEEE Transactions on Vehicular Technology, 2009, 58(4):1804-1815.

[33] 宋云飞, 卢光跃. 基于采样协方差矩阵的频谱感知算法仿真分析[J].西安邮电学院学报,2011,16(5):12-16.

[34] Yang Xi, Lei Kejun, Peng Shengliang, et al. Blind Detection for Primary User Based on the Sample Covariance Matrix in Cognitive Radio[J]. IEEE Communications Letters, 2011,15 (1):40-42.

[35] 赵佩, 包志强, 卢光跃. 基于最大相关系数的盲频谱感知算法[C]//2012年全国无线电应用与管理学术会议(CRAM’12).北京:电子工业出版社,2012:151-156.

[36] Bao Zhiqiang, Zhao Pei, Lu Guangyue. Blind Spectrum Sensing Method Based on the Maximum Correlation Coefficient And Use There of: United States Application or PCT International Application Number:13/973344[P], 2013-08-22.

[37] Cabric D, Tkachenko A, Brodersen R W. Spectrum Sensing Measurements of Pilot,Energy,and Collaborative Detection[C]//Military Communications Conference. USA Washington: IEEE, 2006:1-7.

[38] Budiarjo I, Lakshmanan M K, Nikookar H. Cognitive Radio Dynamic Access Techniques[J]. Wireless Personal Communications,2008,45(3):293-324.

[39] Urkowitz H. Energy Detection of Unknown Deterministic Signals[J]. Proceedings of the IEEE,1967,55(4):523-531.

[40] Tandra R, Sahai A. SNR Walls for Signal Detection[J]. IEEE Journal of Selected Topics in Signal Processing, 2008,2(1):4-17.

[41] Gardner W A. Signal Interception:A Unifying Theoretical Framework for Feature Detection[J]. IEEE Transactions on Communications,1988,36(8):897- 906.

[42] Fehske A, Gaeddert J, Reed J. A New Approach to Signal Classification Using Spectral Correlation and Neural Networks[C]//2005 First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks. USA VA Mclean: IEEE DySPAN, 2005:144-150.

[43] Lunden J, Koivunen V, Huttunen A, et al. Collaborative Cyclostationary Spectrum Sensing for Cognitive Radio Systems[J]. IEEE Transactions on Signal Processing,2009,57(11):4182-4195.

[44] Bai Zhidong. A Review: Methodologies in Spectral Analysis of Large Dimensional Random Matrice[J].Statistica Sinica,1999,9(3):611-677.

[45] Baik J, Ben Arous G, Peche S. Phase Transition of the Largest Eigenvalue for Nonnull Complex Sample Covariance Matrices[J]. Annals of Probability, 2005,33(5):1643-1697.

[46] Dikmese S, Renfors M. Performance Analysis of Eigenvalue Based Spectrum Sensing under Frequency Selective Channels[C]//2012 7th International ICST Conference on Cognitive Radio Oriented Wireless Networks and Communications. Sweden Stockholm:IEEE, 2012:356-361.

[47] Penna F, GarelloR, Spirito M A. Cooperative Spectrum Sensing Based on the Limiting Eigenvalue Ratio Distribution in Wishart Matrices[J]. IEEE Communications Letters, 2009,13(7):507-509.

[48] Liu Shulei, Shen J, Zhang R, et al. Information Theoretic Criterion-based Spectrum Sensing for Cognitive Radio[J]. IET Communication, 2008,2(6):753-762.

[49] 王磊, 郑宝玉, 崔景伍. 基于随机矩阵理论的频谱感知技术研究综述[J].信号处理,2011,27(12):1889-1897.

[50] Tulino A M, Verdu S. Random Matrix Theory and Wireless Communications[M]. USA Hanover: Now Publisher Inc,2004:3-73.

[51] Johnstone I M. On the distribution of the largest eigenvalue in principle components analysis[J]. Annals of statistics, 2001,29(2):295-327.

[责任编辑:王辉]

Cooperative spectrum sensing algorithms based oneigenvalue structure of the

signal

LU Guangyue, MI Yin, BAO Zhiqiang, FENG Jingyu

(National Engineering Laboratory for Wireless Security, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

In order to fully understand the current spectrum sensing(SS) technology in cognitive radio(CR), and thorough research muti-node cooperative SS algorithms based on eigenvalue structure, the recent development of random matrix theory(RMT) has been introduced into the field of SS, thereby the performance of SS is greatly improved, SS may be realized in the practical applications. Through elaborating the basic principle of the cooperative SS schemes based on the sample covariance matrix and eigenvalues, the main characteristics of the SS scheme are generalized and the methods for the threshold decision are deduced. By simulation experiments with Matlab, the performance of algorithms is compared and verified. The future research trends are given in the end.

cognitive radio, spectrum sensing, random matrix theory, sample covariance matrix, eigenvalue

2014-01-01

国家科技重大专项基金资助项目(2012ZX03001025-004)；国家自然科学基金资助项目(61271276, 61301091)；工业和信息化部通信软科学基金资助项目(2013R36-2,2014R33)；陕西省自然科学基金资助项目(2012JQ8011)；陕西省教育厅自然科学基金资助项目(11JK0925)

卢光跃(1971-)，男，博士，教授，从事信号处理研究。E-mail:tonylugy@163.com 弥寅(1986-)，男，硕士研究生，研究方向为认知无线电。E-mail:miyin0404@163.com

10.13682/j.issn.2095-6533.2014.02.001

TN92

A

2095-6533(2014)02-0001-12