基于区域划分的刀轨生成算法的研究
李 骏, 樊留群,赵建华,陈 阁,胡立文
(1.同济大学 中德学院,上海 200092; 2.沈阳机床设计研究院有限公司上海分公司,上海 201804)
基于区域划分的刀轨生成算法的研究
李 骏1, 樊留群1,赵建华2,陈 阁2,胡立文1
(1.同济大学 中德学院,上海 200092; 2.沈阳机床设计研究院有限公司上海分公司,上海 201804)
针对行切法加工带有岛屿的复杂型腔时,如何产生最短且无跳刀的刀具轨迹,提出了一种基于区域划分的刀具轨迹生成算法。首先通过区域划分理论将内外边界均为凸轮廓的复杂型腔的加工区域划分为若干单调子区域,然后在每个单调子区域中生成刀具轨迹,刀具加工完一个子区域,可以直接过渡到相邻子区域,不仅获得了无跳刀刀轨,加工中也不存在重复切削现象。最后将该方法与UG中的往复行切法进行了对比,验证了该算法的有效性。
刀具轨迹;复杂型腔;区域划分;无跳刀
0 引言
型腔加工被广泛应用于航空、汽车、模具制造业等领域,其中平面型腔加工又是型腔加工中应用最广泛的[1]。对于平面型腔加工,主要有行切法和环切法两种走刀方式。行切法又可以分为单向行切(Zig型)和往复行切(Zig-Zag型)。
与环切加工相比,行切加工由于其刀具轨迹主要由一系列与某一恒定方向(如水平方向)平行的长距离直线段组成,既有利于发挥机床的最大进给速度,同时其切削表面质量也好于环切加工[2]。因此,行切加工广泛应用于型腔类工件的粗加工中。但是,对于带有多个岛屿的复杂平面型腔采用行切加工时,常常会产生附加的抬刀动作。在实际加工中,如果在刀具轨迹中存在大量的附加抬刀动作,则会严重降低切削加工的效率与加工质量。因此,如何避免或减少在行切加工过程中产生的跳刀次数多年以来一直是数控加工领域研究的重点[3]。
Held[4-5]把整个切削区域按加工需要分成若干子区域,分别加工各子区域。这种不同的加工域选择,既减少了抬刀次数又不会使加工轨迹相对变长,同时可对新区域采用最合理的走刀方式,提高了加工效率。Tang K[6-7]在Held的基础上就如何减少抬刀次数的问题作了进一步的分析,提出并证明了四条定理,同时给出了一个满足最小跳刀次数的分区算法。盛沛颐和陈钢[8]针对平面型腔行切加工刀具轨迹生成中如何合理而最大程度地减少在加工刀具轨迹中产生的跳刀动作的次数,提出了一种基于单调链技术的行切刀具轨迹生成算法,从而最大程度地减少了平面型腔行切加工时跳刀动作的次数。
上述研究方法有效的减少了型腔行切加工中的跳刀次数,但是没能够实现零跳刀。本文针对内外轮廓均为凸轮廓的复杂型腔提出了一种基于区域划分的刀轨生成算法,通过对加工区域的单调子区域的划分,不仅获得了无跳刀的往复行切刀轨,加工中也不存在重复切削现象,尤其在处理型腔中含有多岛屿的复杂情况时,简化算法和提高运行效率的效果更加突出。
1 基于区域划分的刀轨生成算法的描述
1.1 算法的基本概念
概念1:单调区域
在平面区域A中,如果与直线l平行的每一条直线与区域A的边界(与l平行的边界线除外)的交点最多都只有两个,则区域A被称作直线l的单调区域。
概念2:内轮廓和外轮廓
本文中的外轮廓是指型腔中加工区域的外边界,内轮廓是指型腔中岛屿的外边界。
概念3:轮廓极点
过轮廓的顶点Pn(n=1,2,3…)做水平线使其穿过轮廓,若与Pn相邻的两个顶点Pn-1和Pn+1都在水平线的同一侧,则Pn为轮廓的极点。当Pn-1和Pn+1都在Pn上方时,Pn为极小点;当Pn-1和Pn+1在Pn下方时,Pn为极大点。如图1a所示,P1为轮廓的极大点,P4为轮廓的极小点,P2,P3,P5,P6不是轮廓的极点。若轮廓中含有圆弧,则取圆弧的两个端点及与水平线相切的点作为该段圆弧的顶点。
对于含有水平线段的轮廓(如图1b),可取水平线段的中点作为该线段的唯一顶点。图2b中线段P1P7的中点PM为轮廓的极大点,线段P4P5的中点PN为轮廓的极小点,而线段P2P3上没有极点。

图1 轮廓极点
类似地,过轮廓的顶点Pn做垂直线穿过轮廓,若与Pn相邻的两个顶点Pn-1和Pn+1都在垂直线的右侧,则Pn为轮廓的极左点。当Pn-1和Pn+1都在Pn左侧时,Pn为极右点。
1.2 算法的基本思路
首先对型腔内外轮廓的极点进行判断,然后按一定的原则将轮廓的极点连接,从而将加工区域划分为若干单调子区域。刀具从一个子区域开始加工,当该区域加工完成时,刀具可以直接过渡到相邻的未加工区域,从而在不进行跳刀的情况下完成整个型腔的加工。
1.2.1 单调子区域划分
单调子区域划分步骤如下:
(1)确定复杂型腔内外轮廓的极点;
首先对型腔内外轮廓的极点进行判断,得到外轮廓的极大点Wmax和极小点Wmin,以及内轮廓的极大点Imax和极小点Imin。以外轮廓极小点为原点建立平面直角坐标系,内轮廓的极大点的纵坐标记为Omax,称作内轮廓的极大值;内轮廓的极小点的纵坐标记为Omin,称作内轮廓的极小值。
(2)对内轮廓进行编号;
按内轮廓极大值Omax的大小对内轮廓进行排序,并依次将内轮廓编号为I1,I2,I3,…,In,使其极大值满足条件Omax1≥Omax2≥Omax3≥…≥Omaxn。
(3)标记第一层轮廓;
将I1的极小值Omin1依次与其他内轮廓(从I2开始)的极大值Omax2,Omax3,Omax4等进行比较,找出极大值比Omin1大的最后一个内轮廓Ip,将I1,I2,…,Ip(1≤p≤n)标记为1,即第一层内轮廓。
(4)标记第二层轮廓,并与第一层轮廓生成连线;
在I2,I3,…,Ip中,若其中某个内轮廓Ia的极小值大于另一个轮廓Ib的极大值,则将Ib标记为2,即第二层外轮廓。找出极大值比Omin(p+1)大的最后一个内轮廓Iq,将Ip+1,Ip+2,…,Iq(p (5)标记第三层轮廓,并与第一层和第二层轮廓生成连线; 找出极大值比Omin(q+1)大的最后一个内轮廓It,将Iq+1,Iq+2,…,It(q (6)标记后续层内轮廓,并与前层内轮廓生成连线; 在后续层内轮廓中重复上述操作,直到最终所有内轮廓都标记完毕。 (7)内外轮廓极点间生成连线; 最后将未连线的内轮廓的极小点与外轮廓的极小点相连,标记为1的内轮廓的极大点与外轮廓的极大点相连,型腔的单调子区域划分完毕。 图2 连线与其他内轮廓发生干涉 图3a所示的含多岛屿复杂型腔的加工区域可按以上步骤划分为Ⅰ、Ⅱ、Ⅲ和Ⅳ4个单调子区域(图3b)。 图3 复杂型腔单调子区域划分 1.2.2 刀具轨迹的生成 如果标记为1的内轮廓数目为n,则型腔的加工区域被划分为了n+1个单调子区域。外轮廓的极大点和极小点即为每个子区域的最高点和最低点,这样当刀具加工完一个子区域时,无需跳刀,直接从距外轮廓极点垂直距离为D/2的单调子区域边界处过渡到下一个子区域,直到所有区域加工完毕。 刀具从最左边的子区域Z1开始,生成双向行切线。第一条行切线距离外轮廓的极大点的垂直距离为D/2,方向为水平从左到右。行距的确定采用改进的恒定步距法[9],由于对于每个单调子区域,刀具进入和离开的方向是相反的,因此必须保证行切线的数量为奇数。设刀具直径为D,外轮廓极大点与极小点间的垂直距离为H,切削余量为C0。则当H-D-2C0与D的比值的整数部分,即[(H-D-2C0)/D]为奇数时,行距DL=H/{[(H-D-2C0)/D]+1};当其为偶数时,行距DL=H/{[(H-D-2C0)/D]+2}。 1.3 算法的流程 基于区域划分的刀轨生成算法的流程图如图4所示。 图4 刀具轨迹生成流程图 设有如图5所示的一个具有平面型腔的工件(130mm×130mm×20mm),该工件中包含7个内轮廓 (岛屿)。在UG8.0中分别采用往复行切走刀加工方法和本论文所提出的轨迹生成方法进行仿真铣削粗加工,仿真加工过程中两种加工方法均采用相同的加工参数(如表1)。 图5 复杂平面型腔零件 表1 加工参数 主轴转速(r·min-1)进给速率(mm·min-1)刀具直径(mm)走刀行距(mm)300015006恒定步距法[9] 采用往复行切走刀加工方式生成的刀具轨迹如图6a,采用本论文所介绍的刀具路径规划方法生成的刀具轨迹如图6b(图中实线代表刀具切削轨迹,虚线代表跳刀轨迹)。 表2是在UG8.0仿真加工中所得到的实验数据,对比表2中的数据可以得出:本文算法生成的刀轨由于在加工过程中没有跳刀,刀轨总长度显著缩短,因而大大减少了加工时间(大约10%),提高了加工效率,该方法要明显优于传统往复行切走刀方式。 图6 刀具加工轨迹对比 表2 加工数据对比 参数走刀方式UG中的往复走刀走刀方式切削路径长度(mm)1889.81980.6跳刀路径长度(mm)517.30总路径长度(mm)2407.11980.6跳刀次数80总加工时间(s)98.9388.99 基于区域划分的刀具轨迹生成算法依照区域划分理论将含有多岛屿的复杂型腔的加工区域划分为几个单调的子区域,实现了在复杂型腔加工过程中零跳刀,且无重复加工。轨迹连续性好,加工时间短,大大地提高了复杂型腔铣削粗加工时的加工效率。但目前只适用于型腔的内外轮廓均为凸轮廓的情况,对于内外轮廓中含有凹点的型腔,目前还没有简单有效的单调子 区域划分方法,这将是以后的研究方向。 [1] 陈英俊,陈小童.MasterCAM在复杂曲面数控铣削加工中的应用研究[J].组合机床与自动化加工技术,2013(4):96-98. [2] 童伟,申戈琍.数控铣削加工走刀方式的研究.中国电子学会电子机械工程分会2007年机械电子学学术会议论文集,2007. [3] 董光雷,戴宁,杨峰,等.环切刀轨无跳刀过渡连接算法[J].中国机械工程,2012,23(8):1896-1902. [4] Held M, Arkin, E. M.: Letter to Editor: An Algorithm for Reducing Tool Retractions in Zigzag Pocket Machining. Computer-Aided Design 2000,32(10):917-919. [5] Held M. geometry-based investigation of the tool path generation for zigzag pocket machining. Visual Computer, 7(5/6)1991,296-308. [6] Tang K. Geometric Optimization Algorithms in Manufacturing. Computer Aided Design and Applications, 2005,2(6):747-758. [7] Tang K, Chou S Y, Chen L L. An algorithm for reducing tool retractions in zigzag pocket machining. Computer-Aided Design,1998,30:123-129. [8] 盛沛颐,陈钢,张新访.基于单调链的平面型腔行切加工轨迹生成算法[J].华中科技大学学报(自然科学版),2002(4):10-12. [9] 王卫兵.UG NX6数控编程实用教程(第2版)[M].北京:清华大学出版社,2010. [10]田春霞.数控铣削刀具路径的规划[J].组合机床与自动化加工技术,2008(11):72-75. (编辑 李秀敏) Research about Generation Algorithm of Tool Path based on Area Dividing LI Jun1,FAN Liu-qun1,ZHAO Jian-hua2,CHEN Ge2, HU Li-wen1 (1.Sino-German College, Tongji-University, Shanghai 200092, China; 2. SMTCL Research Institute, Shanghai 201804, China) An algorithm for tool path generation based on area dividing method, in order to generate the shortest path without tool retraction in a zigzag pocket machining of complex cavity with many convex islands, is given in this paper. Firstly, processing area of complex cavity whose inside and outside boundaries are both convex contour is divided into several monotony sub-regions through area dividing method. Then tool paths are generated in all monotony sub-regions. After the processing of a sub-region is finished, tool can directly transit into the next adjacent region. In this way, not only a tool path without tool retraction can be acquired, but also during the processing it doesn’t exist repeat cutting. Finally, it is compared with the zigzag cutting method in UG to illustrate the effectiveness of this algorithm. tool path; complex cavity; area dividing; without tool retraction 1001-2265(2014)05-0123-04 10.13462/j.cnki.mmtamt.2014.05.032 2013-08-21; 2013-09-21 李骏(1990—),男,河北邢台人,同济大学硕士研究生,主要研究方向为数控加工技术,(E-mail) lijun_china@126.com。 TH166;TG65 A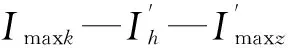



2 实例验证

3 结束语

