TX1600G镗铣加工中心龙门铣削系统动态特性分析*

刘傲翔，王 军，，康俊贤，舒启林

(1.沈阳建筑大学 交通与机械工程学院，沈阳 110168；2.沈阳理工大学 机械工程学院，沈阳 110159)

TX1600G镗铣加工中心龙门铣削系统动态特性分析*

刘傲翔1，王 军1，2，康俊贤1，舒启林2

(1.沈阳建筑大学 交通与机械工程学院，沈阳 110168；2.沈阳理工大学 机械工程学院，沈阳 110159)

以TX1600G镗铣加工中心铣削系统为研究对象，利用Solidworks建立了铣削系统的三维实体模型。同时利用有限元分析软件ANSYS Workbench 对机床铣削系统进行模态分析，获得其前六阶固有频率及振型。并在模态分析的基础上对铣削系统进行谐响应分析，得到了系统沿三个主运动方向的幅频曲线，进一步探讨铣削系统在外力激力下的抗振性能，并验证了有限元模型的有效性。通过模态、谐响应分析，验证了模型简化方案的可行性，在选择具体的材料方面，提供了良好的依据。同时，为以后镗铣加工中心铣削系统机电联合仿真参数优化设计奠定了夯实的基础。

镗铣加工中心；铣削系统；模态分析；谐响应；机电联合仿真

0 引言

随着精密加工技术的不断发展，对零件的加工质量要求越来越高。机床在高转速工作时，切削力的实时变化及外界环境等因素的作用会使机床产生振动，严重降低了工件的加工精度及表面质量；同时，振动还会降低加工效率，加快刀具的磨损，进而影响整机切削运动的稳定性。因此，掌握加工中心动态特性是改进加工中心性能，提高加工精度一个关键因素[1-2]。

机床结构的动态特性分析包括机床的模态分析和谐响应分析。模态分析是分析机械结构的固有振动特性,如每一阶模态的固有频率、阻尼比和振型等，其目的是分析系统的振动及刚度特点，使系统避开共振现象[3-6]。谐响应分析是用于确定线性结构在承受随时间按正弦规律变化的载荷时的稳态响应，其目的在于验证机床能否克服共振和疲劳等不利因素[7-8]。

本文在ANSYS Workbench环境下,针对TX1600G镗铣加工中心铣削系统进行动态特性分析，得到结构的前六阶固有频率、振型以及谐响应规律，明确机械系统整体的动态特性,验证有限元模型的准确性，并为今后整机的机电联合仿真参数优化设计奠定基础。

1 TX1600G镗铣加工中心介绍

图1为TX1600G镗铣加工中心结构示意图，其主要部件分别为床身、铣立柱、横梁、铣滑台，主轴箱、镗立柱、镗滑台、滑枕、工作台。该镗铣加工中心结合了镗床和铣床的结构特征，具有镗削、铣削2个主轴，针对于大型复杂箱体类零件，在一次装夹的情况下，可以实现其多个表面的镗、铣、钻等工序的复合加工问题，避免多次装夹造成的精度降低和搬运不便。

铣削系统是镗铣加工中心的关键系统，其动态性能会直接影响到整个加工中心的加工精度、运动稳定性、抗振性能以及使用寿命。因此,在结构设计时,铣削系统的动态特性是关注的焦点。

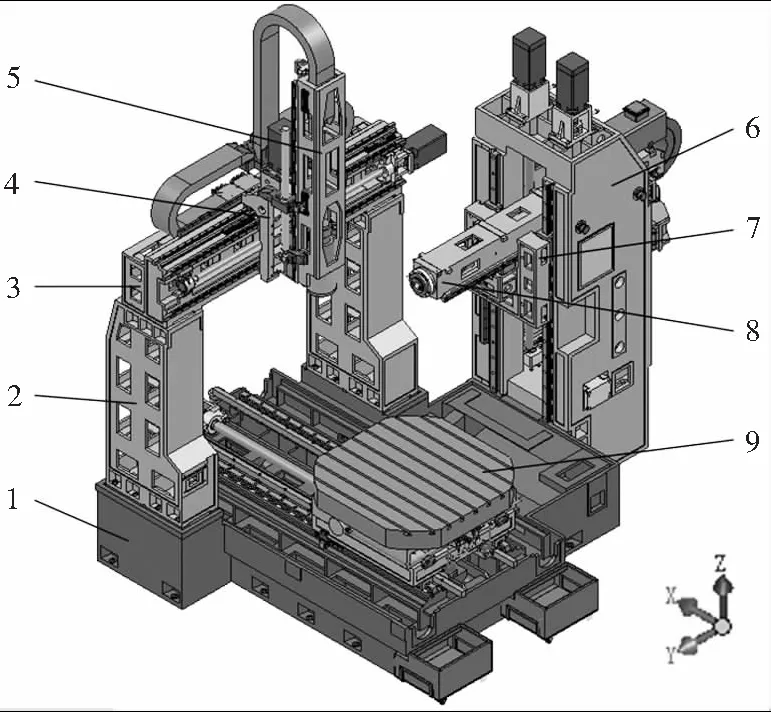
1.床身 2.铣立柱 3.横梁 4.铣滑台 5.主轴箱 6.镗立柱 7.镗滑台 8.滑枕 9.工作台图1 TX1600G镗铣加工中心模型

2 高速高加速度下机械系统动态性能

TX1600G镗铣加工中心在加工过程中，机械系统的位置和速度是不断变化的，铣削主轴的转速最高达到了24000r/min，此外，启动和停止的换向过程中，由于速度变化带来的惯性力变化，都会对机械系统的动态特性产生重要的影响，即由于空间位置的不同，不同速度下不同的阻尼特性，不同加速度下由于动结合部非线性的作用导致的刚度不同，系统的动力学微分方程(式(1))中的系数矩阵均不是恒定的，是随着进给运动参数而发生变化，其所引起的弹性变形和振动特性变化,将会直接影响系统的传动精度和稳定性[9]。

(1)

式(1)中:[M]、[C]、[K]分别为机构的质量、阻尼以及刚度矩阵;

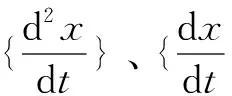
机械系统所受到的切削力、伺服驱动力以及外界干扰在高速高加速度的工况下，都将会变得更加复杂，其动态特性的变化对机电耦合作用的最终结果有着重要的影响[9]。

3 模态分析

3.1 模态分析基本原理

当在无阻尼、无激振力的情况下，系统振动微分方程为：

(2)

当分析铣削系统固有频率需将时域信号转换为频域信号，对方程(2)进行拉普拉斯变换，拉氏算子为s=jω，令其初始条件为零，则:

([K]-ω2[M]){X(ω)}=0

(3)

式(3)中:ω2为系统特征值,即:系统固有频率;{x}为系统特征向量,即:系统振型。由方程(3)可知,系统的固有振动特性仅与其本身的质量分布和刚度有关。

3.2 模态分析过程

利用Solidworks软件建立了组合体的实体模型，利用软件之间数据接口将实体模型导入ANSYS Workbench软件中，并且建立铣削系统的有限元模型如图2，由于铣削系统结构比较复杂，在建模过程中必须对模型进行合理简化，例如删除倒角、小孔、小凸台及非承载系统等，通过简化，既提高了工作效率，又能确保分析结果的准确性。

定义材料属性：在铣削系统中，横梁、立柱、滑台、主轴箱的材料HT300,设定其弹性模量157GPa，泊松比0.23，密度7.352×103kg/m3，导轨的材料40Cr，设定其弹性模量206GP，泊松比0.25，密度7.82×103kg/m3。

定义接触方式：利用workbench内置的非线性接触的模态分析求解器NLMA对含有运动副的机床模型进行模态求解，但需注意，处于固定状态的机床，驱动电机都是锁死状态，需要将其对应的P副定义为绑定Fixed，其余系统则根据实际情况定义成移动副。

划分网格：运用ANSYS workbench的自由网格划分功能进行网格划分时，该铣削系统共生成3569917个节点，1662766个单元。

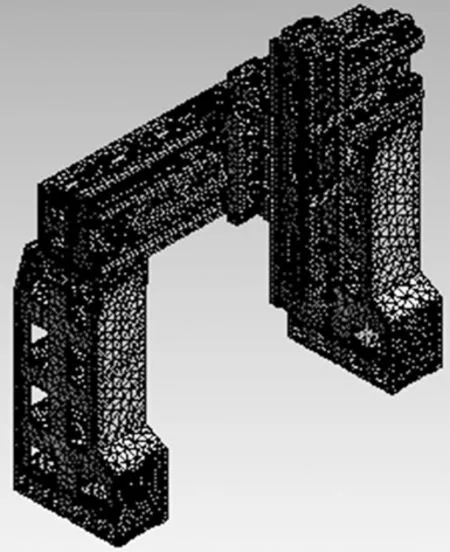
图2 铣削系统的有限元模型

施加约束：双立柱的底面采用固定约束方式。其余各系统接触面均为刚性连接。

求解固有频率和振型：由于机床的振动特征可以表示为各阶固有振型的叠加，其中低阶振型对整个机构的动态特性影响较大。所以，分析过程中使用空间迭代法提取前六阶模态，固有频率如表1所示，各阶振型如图3所示。

表1 固有频率及振型图

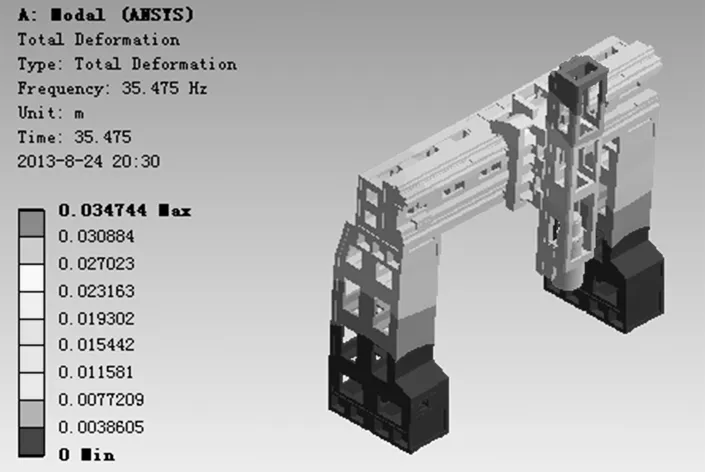
(a)一阶振型图

(b)二阶振型图

(c)三阶振型图

(d)四阶振型图

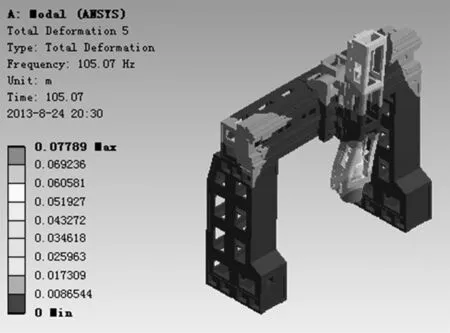
(e)五阶振型图

(f)六阶振型图图3 铣削系统前六阶阵型图

由模态分析结果可知，一阶固有频率为35.475Hz，振型图反映了重力或Y向作用的外力对机床变形的影响，变形最敏感方向沿Y向。沿Y向切削力的频率，若采用六齿面铣刀，主轴转速10000r/min时，则切削力的频率为1000Hz，远大于其固有频率值，切削力引起的机床振动很小。龙门铣削系统的一阶和二阶模态振型表示着主轴箱分别沿Y、X方向的摆动，二者固有频率接近，说明机床沿两方向摆动的刚度相差不大，以上结果的产生是由铣削系统结构上的对称性决定的。三阶和四阶模态振型代表着主轴箱绕X轴、Y轴的转动，其固有频率大于第一、二阶的固有频率，说明机床相对两轴扭曲的刚度大于移动的刚度。

从振型图可知五阶模态的位移最大，发生在铣头处，对铣削系统的影响最大，直接影响工件的加工精度和表面质量。因此，在结构设计的过程中，有必要加强主轴箱、铣头的刚度，来减小系统误差。

4 谐响应分析

由于整机在工作过程中所受切削力是动态变化的，所以铣削系统所受的力也是不稳定的，因此有必要对铣削系统进行谐响应分析，获得铣削系统在随时间正弦规律变化时载荷的稳态响应。通过求得的位移频率响应曲线，分析了铣削系统在动态加载时的抗振特性以及铣削机构能否克服共振等引起的不良影响。查阅金属切削手册[10]端铣平面时主铣削力计算公式为：

(4)

在(4)式中：Fc为主铣削力(铣削力在铣刀主运动方向上的分力)，N；Pc为铣削功率，kW；vc为铣削速度，m/min。

在该铣削加工中，铣削功率Pc=22.356kW，铣削速度vc=1507.97m/min，由公式(4)求得：Fc=889.51N。

由文献[10]可知：

纵向铣削分力Ff=0.35Fc=311.33N，

垂直铣削分力FfN=0.9Fc=800.56N

横向铣削分力Fe=0.525Fc=466.99N

这三个方向的力作用在铣刀上，沿全局坐标系的X、Y、Z轴方向分别作用于铣削系统，由于低频的振动对铣削系统的动态性能影响较大，而且由于系统阻尼作用,响应中的高阶系统衰减很快,故选取前六阶固有频率为研究对象，由模态分析可知，铣削系统第1阶固有频率为35.475Hz，六阶为123.29Hz，所以设置激振频率范围为0～140Hz。载荷的子步数为70，则在该频段可得到70个谐响应解。铣削系统沿全局坐标系的X、Y、Z方向的幅频曲线，如图4所示。

(a)X方向的幅频曲线

(b)Y方向的幅频曲线

(c)Z方向的幅频曲线图4 铣削系统位移频率响应曲线

由图4得到的幅频曲线可知：铣削系统沿X、Y和Z向的各阶频率处都产生较大响应，这与模态分析的结果是匹配的，其结果进一步了有限元模型的有效性。由位移频率图可以看出，激振力频率在37Hz时，机床的频响应最大。说明机床对37Hz频率的外力最为敏感。主要表现为主轴箱绕Y轴的摆动，空间频响应为0.584mm。因此，减轻主轴箱的质量及提高相应结合系统刚度,均可改善机床结构的动态性能。另外，机构沿X向和沿Z向响应接近，这是由于铣削系统结构的对称性决定的，使得在该方向抵消一系统振幅。同时，

Z向的振幅几乎是X向、Y向的2倍，这主要是由于铣削系统的Z向刚度小于X向和Y向刚度所造成的。从位移频率响应曲线的数值可以看出，在不发生共振时，并联机床在工作的三个方向的响应数值一般在0.01mm级。如果需要使铣削系统达到更高的精度标准，可以从提高三个方向的动刚度入手。

5 总结

(1)基于Solidworks和ANSYS Workbench软件,建立了TX1600G镗铣加工中心铣削系统有限元模型，通过模态分析，获得了其前六阶固有频率及振形变化形式，确定了影响整机动态性能的关键系统及结构中的薄弱环节,并提出了改善途径。结果表明铣头部分的刚度较弱，铣削系统刚度和固有频率呈现正相关的变化趋势，因此，有必要加强机构系统的刚度，提高系统稳定性。

(2)在此基础上进行谐响应分析，获得了铣削系统的幅频曲线，分析了铣削系统的谐响应规律，结果表明铣削系统沿X、Y和Z方向的前六阶频率处，都产生较大响应。此外，机床对37Hz频率的外力最为敏感，机床的频响应最大。如果需要使机床达到更高的精度标准，需提高其动刚度。

(3)铣削系统动态特性分析是对其机电耦合作用进行分析最有效的基础之一，为以后镗铣加工中心铣削系统机电联合仿真参数优化设计以及整机向更高精度发展提供了的支持。

[1] Bossoni S. Geometric and dynamic evaluation and optimization of machining centers[D]. Diss., Eidgenössische Technische Hochschule ETH Zürich, Nr. 18382, 2009,2009.

[2] 叶佩青, 王仁彻, 赵彤, 等. 机床整机动态特性研究进展[J]. 清华大学学报: 自然科学版, 2012, 52(12): 1758-1763.

[3] Einziger P, Ben-shmuel E, Bilchinsky A, et al. MODAL ANALYSIS: U.S. Patent 20,130,048,881[P]. 2013-2-28.

[4] 李初晔, 王海涛, 冯长征, 等. 高速数控龙门铣床有限元分析[J]. 制造技术与机床, 2013 (2):75-79.

[5] 史安娜, 孙伟. BW60HS 卧式加工中心整机模态测试[J]. 组合机床与自动化加工技术, 2011 (2): 46-49.

[6] Aenlle M L, Brincker R. Modal scaling in operational modal analysis using a finite element model[J]. International Journal of Mechanical Sciences, 2013,76:86-101.

[7] 董旭, 李蕊, 杨墨. 三自由度并联机床动态有限元分析[J]. 组合机床与自动化加工技术, 2012 (6): 49-52.

[8] Wu Z, Xu C, Zhang J, et al.Modal and Harmonic Reponse Analysis and Evaluation of Machine Tools[C]//Digital Manufacturing and Automation (ICDMA), 2010 International Conference on.IEEE,2010,1:929-933.

[9] 卢秉恒, 赵万华, 张俊, 等. 高速高加速度下的进给系统机电耦合[J]. 机械工程学报, 2013, 49(6):2-11.

[10]上海金属切削技术协会，金属切削手册[M]，上海：上海科学技术出版社，2004.

(编辑 李秀敏)

Dynamic Performance Analysis of TX1600G Boring and Milling Machining Center Milling Systems

LIU Ao-xiang1,WANG Jun1,2,KANG Jun-xian1,SHU Qi-lin2

(1.Traffic and Mechanical Engineering school，Shenyang Jianzhu University，Shenyang 110168，China ;2. Mechanical Engineering school，Shenyang Ligong University，Shenyang 110159 ,China)

TX1600G boring and milling machining center milling parts as the object of the study. The Three -dimensional solid model of was established based on Solidworks. Simultaneously, modal analysis was carried out by ANSYS Workbench software, The first six natural frequencies and corresponding modes were acquired. based on the modal analysis, the harmonic response analysis of milling parts was conducted，and the response curves of the three main motion orientation are obtained respectively，further the milling parts vibration performance under forces is explored，and verifies the validity of the finite element model. The feasibility of the model to simplify the program is verified by modal and harmonic response analysis. The study provides a good basis in terms of selecting a specific material. Meanwhile, the study will lay a solid foundation of the Optimization Design on electromechanical co-simulation of the boring and milling machining center milling parts.

boring-milling machine center; milling system; modal analysis; harmonic response；electromechanical co-simulation

1001-2265(2014)05-0050-04

10.13462/j.cnki.mmtamt.2014.05.013

2013-12-30；

2014-01-09

国家863计划重大项目(2012AA041303);辽宁省科技计划项目(2013220017)

刘傲翔(1989—)，男，辽宁盘锦人，沈阳建筑大学硕士研究生，主要研究方向为镗铣加工中心机电一体化技术，(E-mail)liuaoxiang1989@126.com；王军(1956—)，男，沈阳人，沈阳建筑大学、沈阳理工大学教授，博士生导师，主要研究方向为数字化设计制造技术与应用,(E-mail)wangjun@sjzu.edu.cn。

TH113;TG65

A