震后恢复期物资配送中的多周期选址—联运问题

郑斌，马祖军

（1.西南交通大学峨眉校区,四川峨眉山614202； 2.西南交通大学经济管理学院物流与应急管理研究所,成都610031）

震后恢复期物资配送中的多周期选址—联运问题

郑斌*1，马祖军2

（1.西南交通大学峨眉校区,四川峨眉山614202； 2.西南交通大学经济管理学院物流与应急管理研究所,成都610031）

震后恢复期的物资配送是一项复杂的系统工程，针对震后恢复期两级救援物资配送系统中的多品种物资、多运输方式、多周期决策等特征，提出了一个以系统总费用最小为目标的混合整数线性规划模型，用以解决震后恢复期救援物流系统中的选址—联运问题.针对该模型的特点，设计了一种结合启发式规则的分周期、分阶段解码的混合遗传算法.以“5.12”汶川大地震恢复期救援物资保障过程构建算例，对该模型和算法进行了实例验证.结果表明，该算法具有较好的性能，可以有效解决震后恢复期物资配送中的多周期选址—联运问题.

系统工程；震后恢复；救援物资；选址—联运问题；混合遗传算法

1 引言

近年来，全球地震灾害频发，给人类造成了巨大危害和损失.而应急物资保障作为震后救援工作的关键，需要在有限时间、空间和资源约束下快速满足应急物资需求，以实现灾害损失最小化.其核心是如何科学合理地布局应急物资配送中心、安排多种运输方式进行应急物资联运.

近年来，国内外学者对震后应急物流系统优化问题进行了不少研究，主要包括震后应急选址问题[1，2]和震后应急物资运输问题[3-5].实际上，震后应急设施选址与物资运输是相互联系、相互制约的，有必要进行集成优化管理，但目前对应急集成选址—运输问题研究相对较少.文献[6]针对自然灾害下的应急物资配送及伤员运送建立了协调优化模型，综合了选址、物资分配及车辆路径安排等问题.文献[7]针对美国联邦应急管理局的应急供应链结构，综合考虑应对自然灾害过程中的临时物流设施选址、应急物资配送安排、车辆调度和路径决策，基于混合整数规划建立了一种多周期集成供应链优化模型.文献[8]建立了以总成本最小为目标的应急物流系统LRP模型.文献[9]和文献[10]分别针对震后应急物资配送过程中的模糊动态定位路径问题及两级设施定位路线安排问题进行建模，并设计算法进行求解.文献[11]考虑灾后两级应急物资配送系统优化问题，建立了一个应急物资中转设施LRP多目标优化模型.

震后应急救援活动是个动态演化的过程，一些学者从不同角度对其进行了阶段划分.例如，文献[12]将人类应对地震灾害的过程概括为五个阶段：灾害发生期、灾民安置期、重建恢复期、灾后建设期、现代发展期.文献[13]以汶川大地震为例将应急管理分为应急准备、应急响应、应急恢复三个阶段.为此，依据震后应急物资需求的紧迫程度，将震后救援物资配送大致分为应急救援阶段和震后恢复阶段，且各自具有显著的特征.

目前有关震后应急物流系统优化问题的研究基本上都针对应急救援阶段，然而震后恢复期的救援物资配送也非常重要.震后恢复期通信设备已完全恢复，路网基本恢复畅通，灾情完全得到掌握和控制.此时灾区对救援物资的需求主要为灾民日常生活类物资，以及灾后重建所需的工程类物资.经过一段时间有计划的采购或生产，所需物资基本能够满足.震后应急阶段所开启的物资配送中心将在震后恢复期逐渐关闭.由于震后恢复期规划期长，每隔一段时间救灾管理中心通过采购、生产、捐赠等获得的物资都会有所变化，灾区根据已经接收的物资量，已消耗的物资量等对各自的需求进行定期更新，因此震后恢复期决策宜采取多周期决策.为此，结合震后恢复期救援物资配送的特点，建立了一个以系统总费用最小为目标的多周期选址—联运模型，并设计一个基于分周期、分阶段解码的混合遗传算法.最后以汶川大地震救援物资配送为背景构造算例进行验证.

2 模型建立

2.1 问题描述

震后恢复期会根据救灾实际逐步关闭应急救援阶段所开启的物资配送中心，并选择合适的运输方式有计划地将多品种物资从灾区外围物资集散点运至灾区附近的物资配送中心，再配至各个受灾点，使得运输费用及物资配送中心运营费用之和最小，如图1所示.其中集散点到配送中心的物资配送为上级物资配送，存在多种运输方式（铁路，公路，航空，水运等），配送中心到受灾点的物资配送为下级物资配送，一般采取灵活性较强的公路运输，从而构成了“集散点—物资配送中心—受灾点”的两级物资配送网络系统.从实际救援工作效率，以及可操作性角度出发，震后救援通常将灾区按照一定的规则（如行政隶属关系）进行区域划分，便于救援工作高效、有序地开展.

震后恢复期救援物资配送系统具有一些明显的特征，具体如下：震后恢复期规划时程长，物资供应、需求情况定期更新，需要多周期动态决策；考虑经济成本因素，逐渐关闭震后应急阶段已经开启的物资配送中心；物资供应点、需求点多，物资需求逐渐减少；物资需求种类多，日常生活用品之外，还有用于灾后恢复的工程设备类物资；从物资集散点到物资配送中心可以选择多种运输方式运输，从物资配送中心到受灾点一般选择较灵活的公路运输.

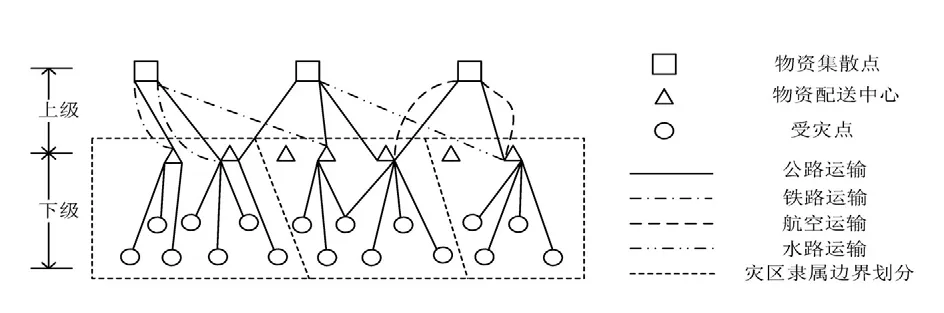
图1 物资配送中的选址－联运问题Fig.1 Framework of Joint Location-Transportation Problem in Relief Distribution

2.2 符号说明

T——物资配送周期集合，t=1,2,…,||T；

SN——物资集散点集合，i∈SN；

R——受灾区域集合，r∈R；

ENr——受灾区域r内已开启的物资配送中心集合，令EN=∪r∈RENr；

DNr——受灾区域r内的受灾点集合，令DN=∪r∈R

DNr；C——物资种类集合，c∈C；

wc——单位物资c的重量，c∈C；

M——物资集散点到物资配送中心的所有运输方式集；

Am——物资集散点到物资配送中心之间存在运输方式m的弧集，m∈M；

A'——受灾区域r内物资配送中心与受灾点

r间存在公路运输的弧集，r∈R；

FCjt——周期t物资配送中心j的运营费用，j∈EN，t∈T；

Thjt：——周期t物资配送中心j的吞吐量限制，j∈EN，t∈T；

sict——周期t物资集散点i对物资c的供应量，i∈SN，c∈C，t∈T；

dkct——周期t受灾点k对物资c的需求量，t∈T，k∈DN，c∈C；

disijm——从物资集散点i到物资配送中心j使用运输方式m运输时的距离，当(i,j)∈Am时，disijm≥0，当(i,j)∉Am时，disijm=+∞，i∈N，j∈N，m∈M；

TCijm——从物资集散点i到物资配送中心j单位距离单位重量物资使用运输方式m运输的平均费用，当(i,j)∈Am时，TCijm≥0，当(i,j)∉Am时，TCijm=+∞，m∈M；

dis′jk——受灾区域r内从物资配送中心j到受灾点k采用公路运输的运输距离，当(j,k)∈A′r时，dis′jk≥0，当(j,k)∉A′r时，dis′jk=+∞，j∈ENr，k∈DNr，r∈R；

TC′jk——受灾区域r内从物资配送中心j到受灾点k单位距离单位重量物资使用公路运输的运输费用，当(j,k)∈A′r时，TC′jk≥0，当(j,k)∉A′r时，TC′jk=+∞，j∈ENr，k∈DNr，r∈R；

B——一个大数；

pijmct——周期t物资c经运输方式m从物资集散点i运至物资配送中心j的量，i∈SN，j∈EN，m∈M，c∈C，t∈T；

i∈SN，j∈EN，m∈M，c∈C，t∈T；

qjkct——周期t物资c从物资配送中心j运至受灾点k的量，j∈ENr，k∈DNr，r∈R，c∈C，t∈T；

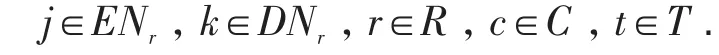
2.3 数学模型

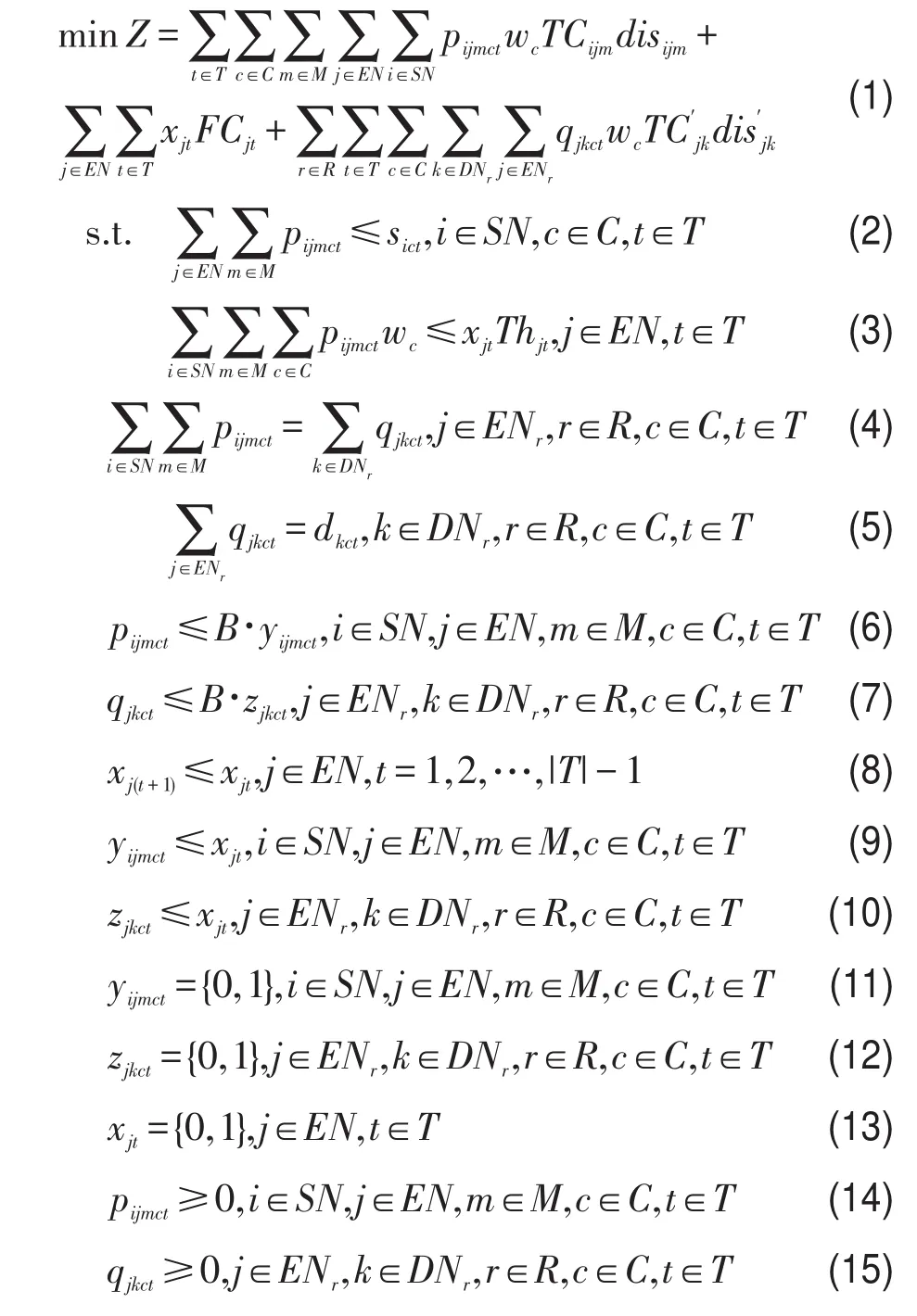
目标函数式(1)使系统总费用最小，式中第一项为上级运输成本，第二项为下级运输成本，第三项为物资配送中心运营成本.约束式(2)表示从物资集散点发出的物资不能超过该点的供应量.约束式(3)表示物资配送中心的吞吐量限制.约束式(4)表示物资配送中心接收的物资量等于其发出量.约束式(5)表示受灾点的接收量等于其需求量.约束式(6)表示某种运输方式只有从某物资集散点出发为某物资配送中心提供某物资时，才能有该物资由该物资集散点发出通过该运输方式运往该物资配送中心.约束式(7)表示下级公路运输只有从某物资配送中心出发为某受灾点提供物资时，才能有该物资从该物资配送中心发出通过公路运输运往该受灾点.约束式(8)表示物资配送中心将逐渐被关闭，已关闭的物资配送中心将不会被重新开启.约束式(9)表示只有当物资配送中心开启时，才能有物资运往该物资配送中心.约束式(10)表示只有当物资配送中心开启时才能有物资从该物资配送中心运往受灾点.约束式(11)-式(13)为0-1变量约束.约束式(14)、式(15)为非负约束.

3 模型求解

上述模型是一个混合整数线性规划模型，包含大量的变量，不仅包括多物资集散点、多受灾点、多物资配送中心、多品种物资、多运输方式，而且涉及多周期决策，计算复杂度随每个变量数量的增加成倍增长，为此设计一个基于分周期、分阶段解码的混合遗传算法来求解该模型.

3.1 参数初始化

设遗传算法的种群规模为popsize，最大迭代次数为maxgen，交叉率Pc，变异率Pm.

3.2 染色体编码和种群初始化

每条染色体由3|T|个子串构成，其中子串3(t-1)+1、3(t-1)+2、3(t-1)+3表示周期t（t=1,2,…,|T|）的选址运输编码.子串3(t-1)+1为自然数编码，为1到|DN|·|C|间的自然数的一组随机排列，长度为|DN|·|C|（|DN|为需求点的数目，|C|为物资种类数目）；子串3(t-1)+2为0-1编码，长度为|EN|（|EN|为物资配送中心数目），基因位取0或1；子串3(t-1)+3为自然数编码，取值为1到|EN|·|C|的自然数的一组随机排列，因此染色体总长度为(|EN|+|DN|)·|C|·|T|+|EN|·|T|.

例如，现有3个物资集散点，2种物资，2个受灾区域受到地震灾害的影响，其中受灾区域1有4个物资配送中心，5个物资需求点，受灾区域2有3个物资配送中心，4个物资需求点，则周期t（t=1,2,…,|T|）的染色体编码的三个子串如图2所示.

图2 混合遗传算法编码示意图Fig.2 Chromosome encoding scheme

根据染色体编码规则随机生成种群规模为popsize的初始种群.

3.3 染色体解码和适应度函数

染色体解码分周期分子串进行解码，由于子串3(t-1)+2为随机0-1编码，可能会出现周期t开启的物资配送中心处理能力不足的情况，即违反了约束式(3)，此时令目标函数值Z=B；否则，按如下步骤进行解码：

Step1对周期t进行解码，令t=1.

Step2令sub1=substring 3(t-1)+1，sbu3= substring3(t-1)+3,如果t=1,sub2=substring3(t-1)+ 2,否则,sub2(l)=τΠ≤tsubstring{3(t-1)+2}(l),l=1,2,…,|EN|.初始化qjkct=0,xjt=0,令THjt=Thjt,∀j∈EN,∀k∈DN，∀c∈C，∀t∈T.

Step3令λ∗=argmax{sub1(l)|l=1,2,…,|DN|· |C|}选择配送的物资种类接收物资的受灾点受灾点所属的受灾区域为受灾点提供物资的物资配送中心运送的物资量

Step4更新物资配送中心的容量受灾点需求量

Step5若dk∗c∗t=0，则更新编码sub1(λ∗)=0，计算若是则转到Step6，否则返回Step3.

Step6用d′jct记录物资配送中心j的物资流量

Step7若d′jct=0，则令sub3((c-1)|EN|+j)=0,∀j∈EN，∀c∈C.初始化pijmct=0，∀i∈SN，∀j∈EN，∀m∈M，∀c∈C，∀t∈T.

Step8令μ∗=argmax{sub3(l)|l=1,2,…,|EN|·选择配送的物资种类接收物资的物资配送中心为物资配送中心提供物资的物资集散点和运输方式的组合配送的物资量

Step9更新物资集散点供应量更新物资配送中心物资流量

Step10若则计算是否为0，若是执行Step11，否则返回Step8.

Step11如果t＜|T|，则令t=t+1，返回Step2，否则执行Step12.

Step12如果pijmct＞0，则yijmct=1，否则yijmct=0；如果qjkct＞0，则zjkct=1，否则zjkct=0，∀i∈SN，∀j∈EN，∀k∈DN，∀c∈C，∀m∈M，∀t∈T.计算如果则否则计算目标函数值Z.

由于模型目标函数是求总成本最小，可采取基于线性排序的适应度计算方法求解适应度函数.设Pos为个体的目标函数值在种群中按从大到小排列的序位，即Pos=1,2,…,num；SP为选择压力，且则适应度函数为

3.4 遗传操作

采用轮盘赌和精英保留相结合的选择策略.对染色体的每个周期的三个子串分别进行交叉变异.其中，子串3(t-1)+1、3(t-1)+3为自然数编码，采取部分匹配交叉和逆转变异.子串3(t-1)+2为0-1编码，可直接采取两点交叉和离散变异.

3.5 终止条件

设最大迭代次数为maxgen，遗传算法迭代maxgen次后结束.

4 算例分析

4.1 算例

结合“5.12”汶川大地震的震后恢复期救援物资保障过程，选取3个物资集散点——省红十字会、双流机场、火车北站，2种救援物资——水泥（单位：袋）和电力设备（单位：台）.3个受灾区域：

灾区一内的物资配送中心为都江堰、茂县、理县、彭州市、汶川、九寨沟、崇州、大邑；受灾点为都江堰、灌口镇、青城山、紫平铺、虹口乡、茂县、富顺、飞虹、黑虎、太平、理县、朴头乡、木卡乡、通化乡、汶川、映秀镇、水磨镇、卧龙镇、雁门、红岩、小金、黑水、松潘、彭州、小鱼洞、通济、三江.

灾区二内的物资配送中心为安县、什邡、绵竹、北川、平武、江油、德阳、绵阳、广汉；受灾点为安县、秀水、宝林、高川、什邡、洛水镇、双盛镇、蓥华镇.

灾区三内的物资配送中心为广元、青川、旺苍、剑阁；受灾点为广元、青川、瓦砾乡、板桥乡、骑马乡、营盘乡、利州区、朝天区、苍溪、剑阁、元坝区.

实际路网中，上级物资集散点到物资配送中心有三种运输方式——飞机、铁路、公路.上级各种运输方式下物资集散点到物资配送中心的距离为实际运输距离，下级物资配送中心到受灾点的距离为实际运输距离.每个周期时长为1个月，供应点的供应量和需求点的需求量如表1、表2所示.

表1 物资集散点的物资供应量Table 1 Supply distribution

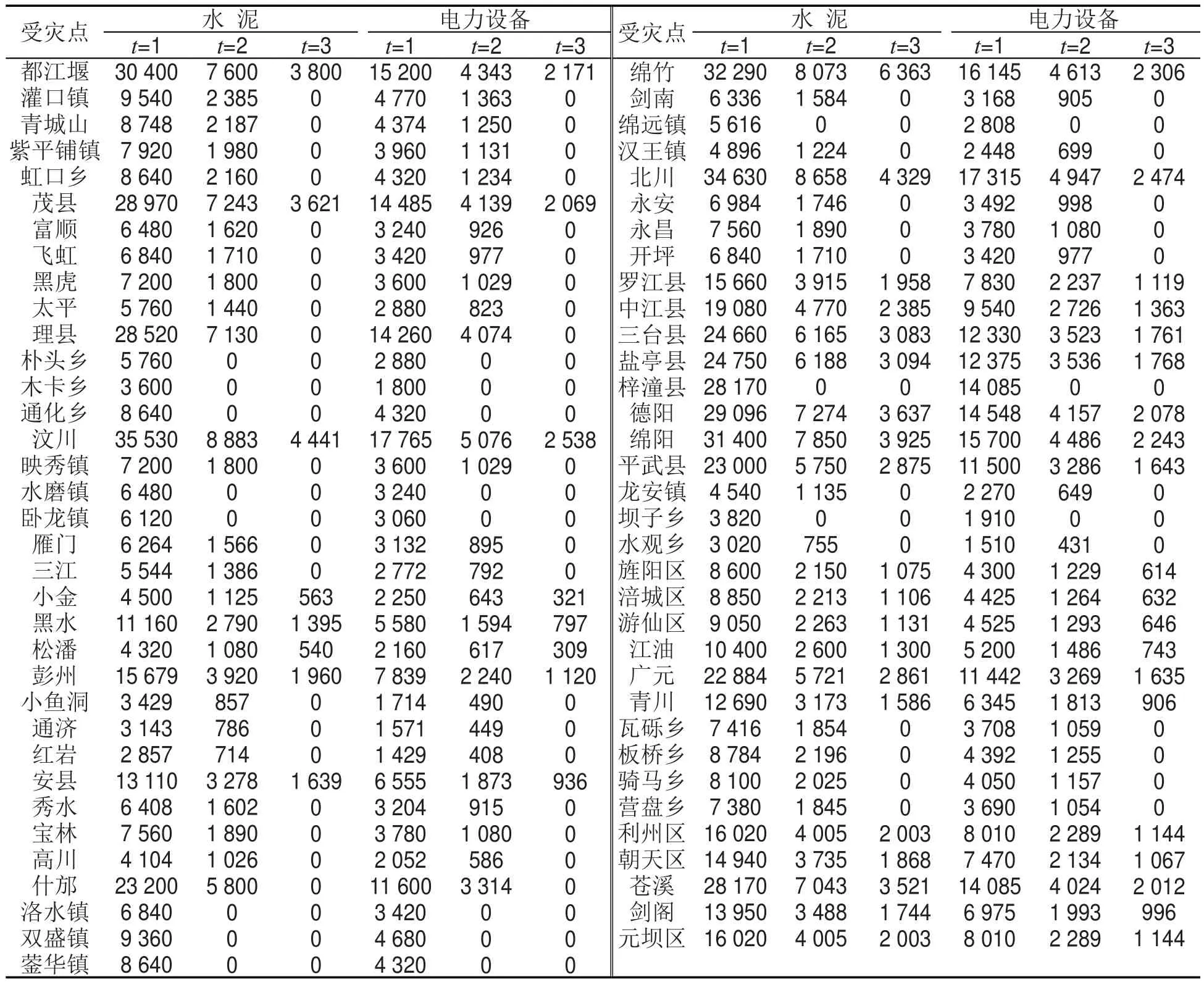
表2 受灾点的物资需求量Table 2 Demand distribution

4.2 计算结果

算法参数设置如下：popsize=100,maxgen= 400,pc=0.95,pm=0.01.采用MATLAB R2010a编程，在Inter(R)Core(TM)2 Duo 2.4GHz CPU和1.96G内存的计算机上运行实现，运行时间为829.3 s，目标函数值为Z=10 075 888.7.表3为各周期物资配送中心的选址情况；图3—图5为三个周期的物资配送结果示意图；图6为震后恢复期算法收敛图计算结果表明，算法收敛效果良好.

表3 物资配送中心选址情况Table 3 The strategies of location

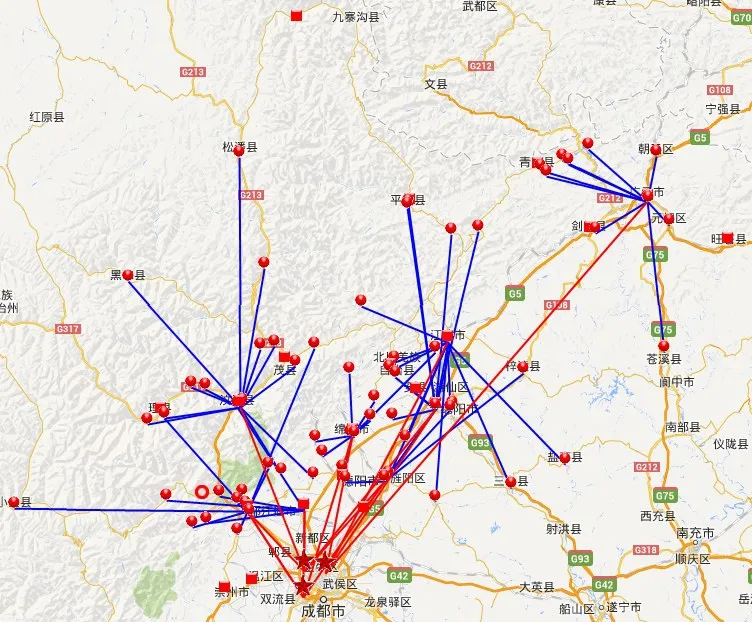
图3 t=1时物资配送结果示意图Fig.3 The result of distribution in the 1stperiod

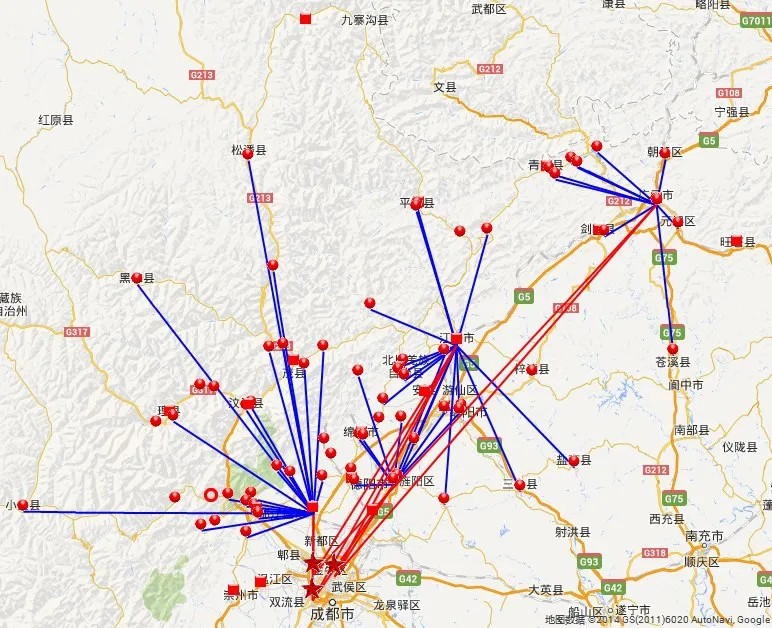
图4 t=2时物资配送结果示意图Fig.4 The result of distribution in the 2ndperiod

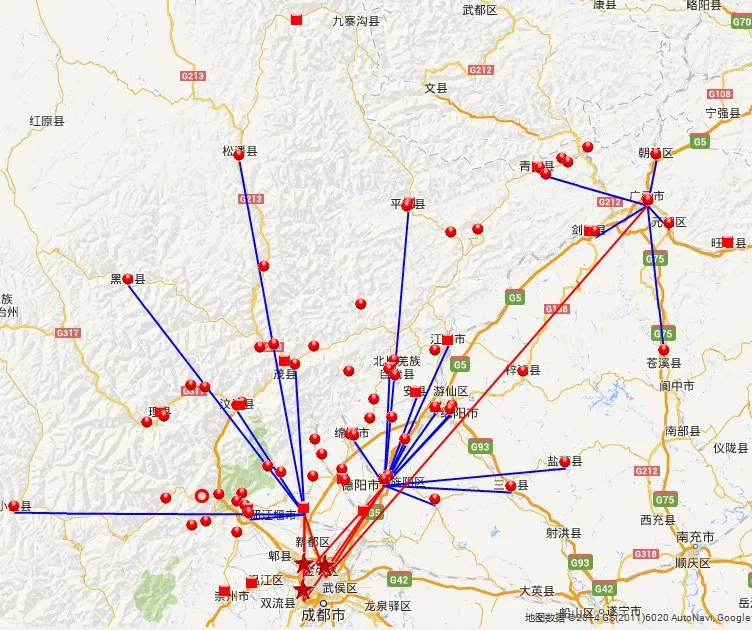
图5 t=3时物资配送结果示意图Fig.5 The result of distribution in the 3rdperiod

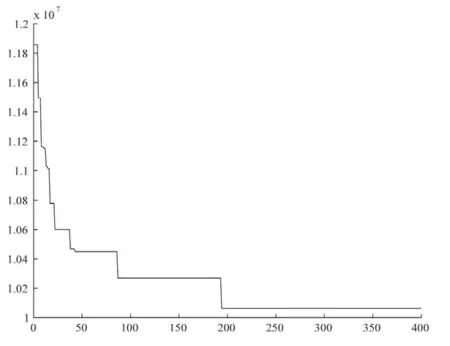
图6 算法收敛图Fig.6 The convergence of the proposed algorithm

从表3可以看出，随着配送任务的减少，逐渐关闭物资配送中心.受篇幅限制，每种运输方式的各种物资的运输量未一一列出.铁路运输平均费用相对较低，与物资集散点——火车站存在铁路运输的物资配送中心有关，如江油、德阳、绵阳、广元都在不同周期选择开启，且在不同周期都能使用铁路运输.

表4给出了种群规模为100，迭代次数为400时，各参数变化时的算法运行时间.计算结果显示，当问题规模小时，用CPLEX求解时间较短，当问题规模较大时，CPLEX计算时间增大明显，混合遗传算法在确保相对差异在5%以内的同时，对大规模问题的求解效率明显高于CPLEX.

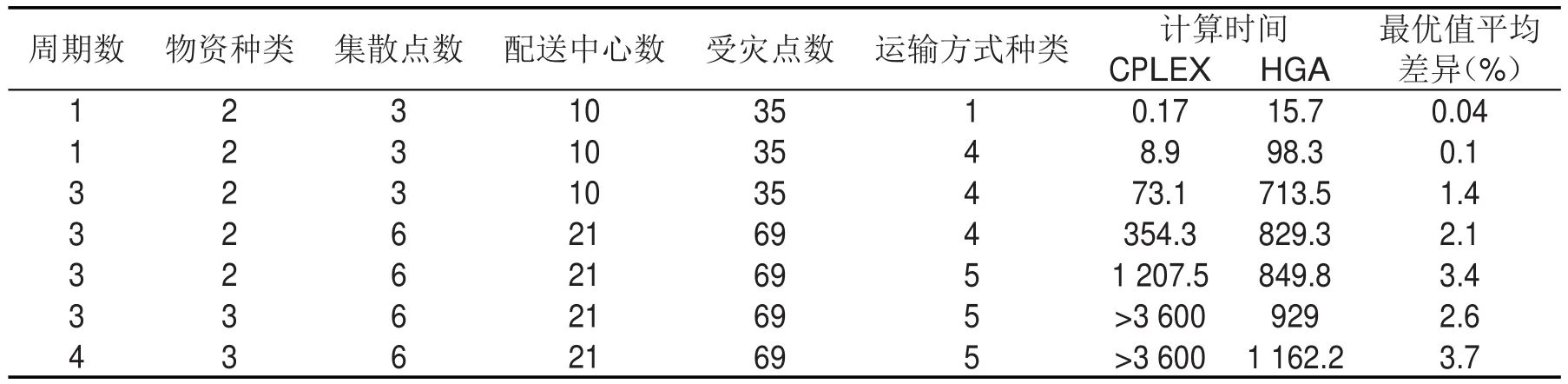
表4 不同参数条件下的算法运行时间及结果对比Table 4 CPU time and result of different size problems

5 研究结论

针对震后恢复期救援物资配送中的选址—联运问题，结合震后恢复期救援物资需求多样化、多运输方式，以及震后恢复期规划时程长，需要进行多周期动态决策等特点，建立了一个以总费用最小为目标的混合整数线性规划模型.并设计了一个基于启发式规则的分周期、分阶段解码的混合遗传算法.最后，以汶川大地震恢复期为背景构造算例，对模型和算法进行验证.结果表明，该混合遗传算法具有较高的计算效率和性能.

[1]Dessouky M,Ordóñez F,Jia H，et al.Rapid distribution of medical supplies[J].Patient Flow:Reducing Delay in Healthcare Delivery,2006:309-338.

[2]Jia H,Ordóñez F,Dessouky M.A modeling framework for facility location of medical services for large-scale emergencies[J].IIE Transactions,2007,39(1):41-55.

[3]Tzeng G H,Cheng H J.Multi-objective optimal plan⁃ning for designing relief delivery systems[J].Transporta⁃tion Research Part E,2007,43(6):673-686.

[4]Widener M J,Horner M W.A hierarchical approach to modeling hurricane disaster relief goods distribution[J]. Journal of Transport Geography,2011,19(4):821-828.

[5]Shen Z,Dessouky M,Ordóñez F.A two-stage vehicle routing model for large-scale bioterrorism emergencies [J].Networks 2009,54:255-269.

[6]Yi W,Özdamar L.A dynamic logistics coordination mod⁃el for evacuation and support in disaster response activi⁃ties[J].European Journal of Operational Research, 2007,179(3):1177-1193.

[7]Afshar A M,Haghani A.Modeling integrated supply chain logistics in real-time large-scale disaster relief operations[J].Socio-EconomicPlanningSciences, 2012,46(4):327-338.

[8]曾敏刚,崔增收,余高辉.基于应急物流的减灾系统LRP研究[J].中国管理科学.2010,18(2):75-80. [ZENG M G,CUI Z S,YU G H.Research on locationrouting problem of relief system based on emergency lo⁃gistics[J].Chinese Journal of Management Science. 2010,18(2):75-80.]

[9]代颖,马祖军,朱道立,等.震后应急物资配送的模糊动态定位一路径问题[J].管理科学学报,2012,15(7): 60-70.[DAI Y,MA Z J,ZHU D L et al.Fuzzy dynamic location-routing problem in post-earthquake delivery of relief materials[J].Journal of Management Sciences in China,2012,15(7):60-70.]

[10]王绍仁,马祖军.震后紧急响应阶段应急物流系统中的LRP[J].系统工程理论与实践.2011,31(8):1497-1507.[WANG S R,MA Z J.Location-routing problem in emergency logistics system for post-earthquake emer⁃gency relief response[J].Systems Engineering-Theory &Practice,2011,31(8):1497-1507.]

[11]Rath S,Gutjahr W J.A math-heuristic for the warehouse location-routing problem in disaster relief[J].Comput⁃ers&Operations Research,2014,42(1):25-39.

[12]胡鞍钢.特大地震灾害的应对周期[J].清华大学学报, 2009,23(4):5-14.[HU A G.The period to combat ex⁃traordinarily earthquake calamities[J].Journal of Tsing⁃hua University,2009,23(4):5-14.]

[13]葛洪磊.基于灾情信息特征的应急物资分配决策模型研究[D].杭州:浙江大学,2012.[GE H L.Study on re⁃lief supplies allocation models based on characteristics of disaster situation information[D].Hangzhou:Zhejiang University,2012.]

Multi-period Joint Location-Transportation during Postearthquake Restoration

ZHENG Bin1,MAZu-jun2
(1.Emei Campus,Southwest Jiaotong University,Emeishan 614202,Sichuan,China;2.Institute for Logistics and Emergency Management,School of Economics and Management,Southwest Jiaotong University,Chengdu 610031,China)

ract:The relief distribution during post-earthquake restoration period is a complex system engineering problem.A mixed integer linear programming model which minimizes the total cost is proposed to describe the joint transfer facility location and transportation problem in a two-echelon relief distribution system.It considers the features of relief distribution during post-earthquake restoration stage,such as various relief materials,various modes of transportation,multi-period decision.etc.Then,a hybrid genetic algorithm with multi-period and multi-phase decoded operation is proposed to solve the model.Finally,the validity of the model and algorithm is demonstrated by a numerical example based on Wenchuan earthquake relief distribution during post-earthquake restoration period.The results show that the proposed genetic algorithm has good performance and is suitable for the joint location-transportation problem in relief distribution.

rds:system engineering;post-earthquake restoration;relief materials;joint location-transportation problem;hybrid genetic algorithm

1009-6744（2014）04-0230-09

F252;U116

A

2013-10-10

2014-02-15录用日期：2014-03-10

国家自然科学基金项目(70771094,90924012)；教育部新世纪优秀人才支持计划资助项目(NCET-10-0706)；四川省哲学社会科学研究规划项目(SC11B049)；中央高校基本科研业务费专项资金资助项目(2682014CX009EM，SWJTU11CX 152,2682013CX073).

郑斌(1983-),女,河北深州市人,讲师.*通讯作者:binzheng@swjtu.cn