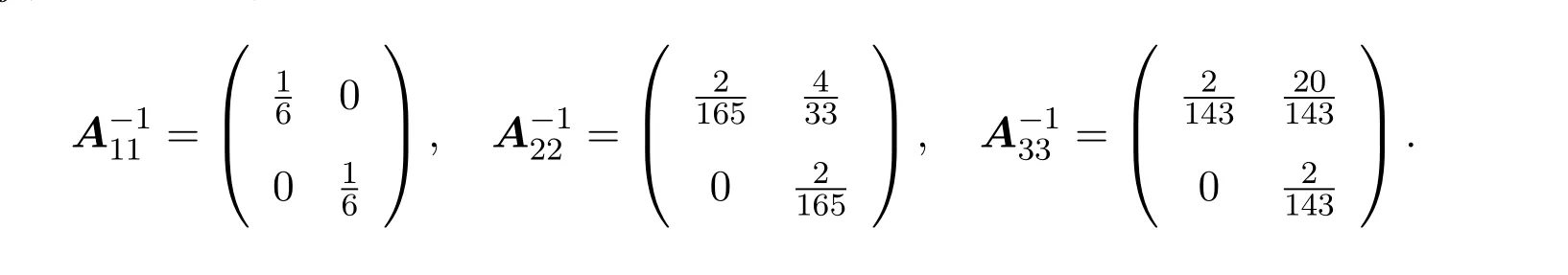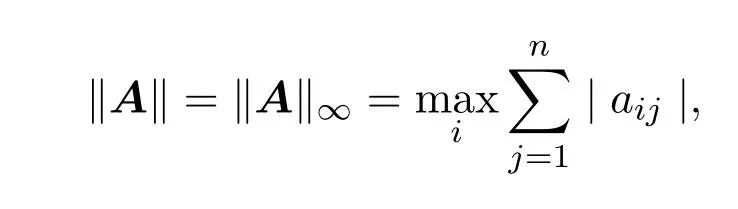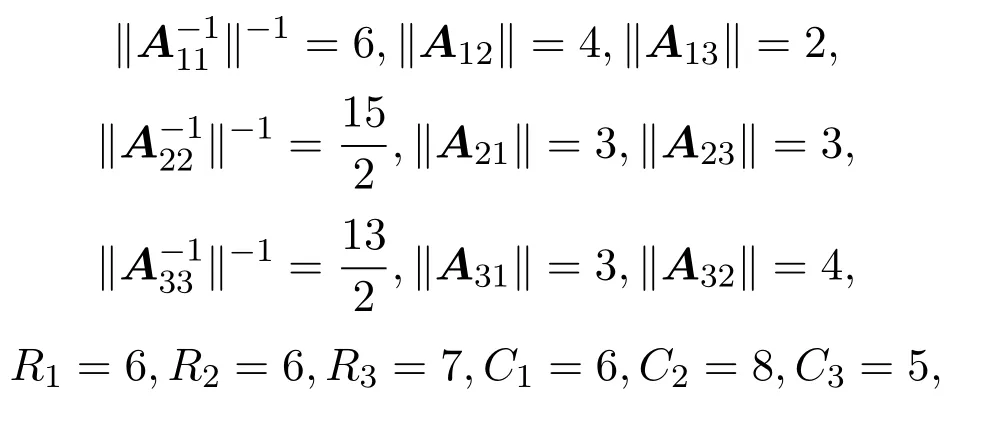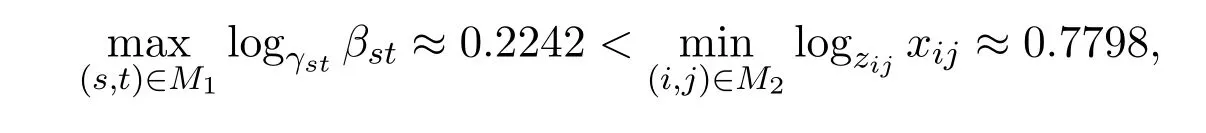块α-对角占优矩阵的讨论
高会双,韩贵春,肖丽霞
(内蒙古民族大学数学学院,内蒙古通辽028043)
块α-对角占优矩阵的讨论
高会双,韩贵春,肖丽霞
(内蒙古民族大学数学学院,内蒙古通辽028043)
应用矩阵块对角占优理论,讨论了块α-对角占优矩阵之间的蕴含关系,并得到了条件最弱的块严格α1-双对角占优的两个等价表征,并作为应用给出了块H矩阵新的判定准则,最后用数值例子说明结果的有效性.
块对角占优;块α-对角占优矩阵;块H矩阵
1 引言
为了适应大规模矩阵计算的需要,矩阵分块技术的应用越来越广泛.因此,众多学者对块对角占优问题进行了研究,获得了一系列重要结果[1-3].本文将块对角占优矩阵概念加以推广,引入块α-对角占优矩阵的定义,给出块严格α1-双对角占优的等价表征,并得到块H矩阵新的判定准则,最后用数值例子说明结果的有效性.
设A=(aij)∈Cn×n为n阶复方阵,分块如下:
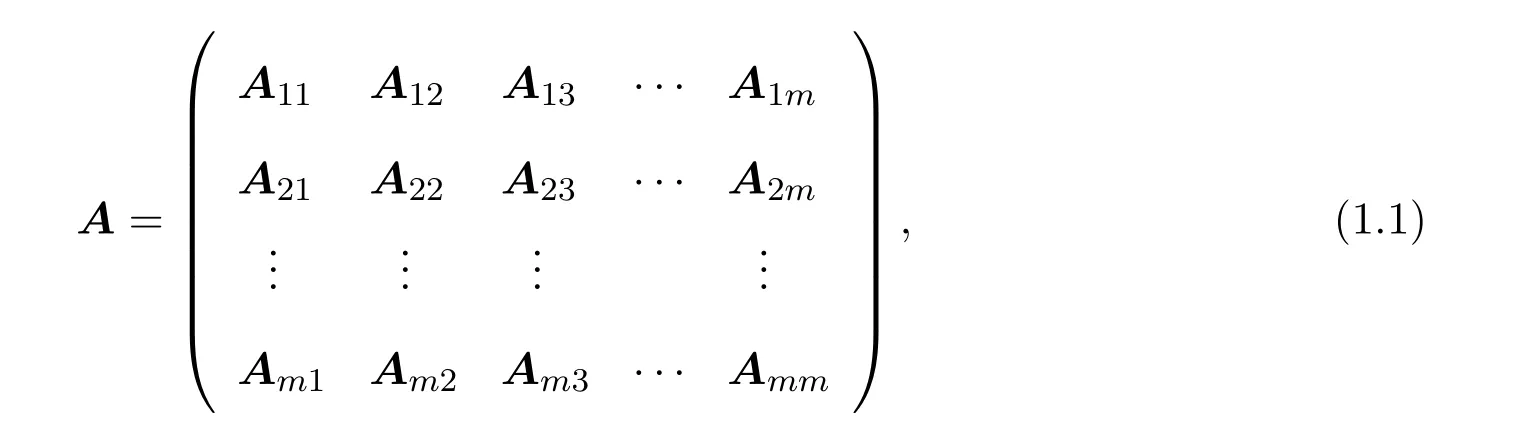
其中Aii为ni阶复方阵,设
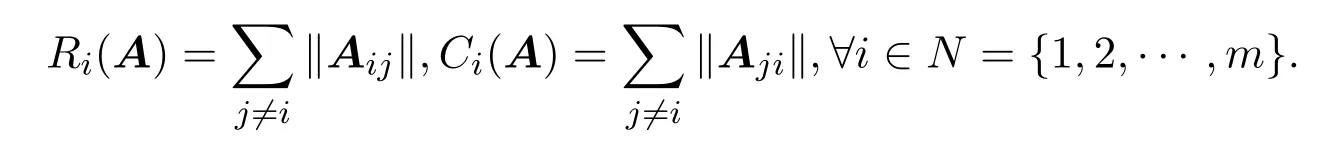
这里矩阵的范数∥·∥为诱导范数.Ri(A),Ci(A)分别简记为Ri,Ci.

由上述知M=M1∪M2∪M3∪M4∪M5∪M6.再记
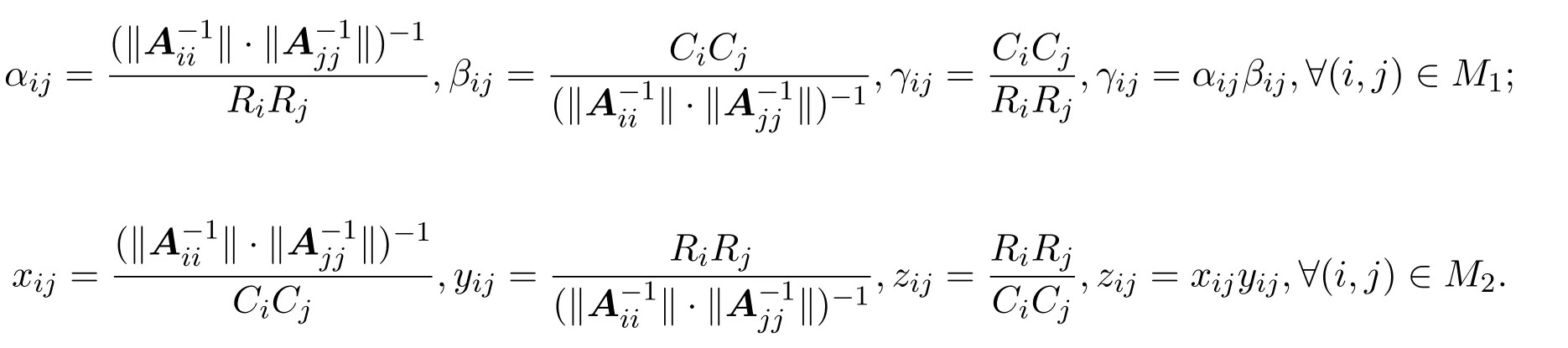
为了行文方便,在下面的定义中给出五种块α-对角占优矩阵的记号.
定义1.1?分块如式(1.1).若存在α∈[0,1],使得
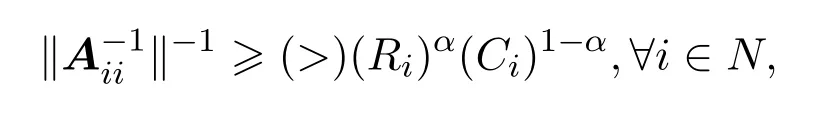
则称矩阵A为块(严格)α1-对角占优矩阵,记为BD1(α0)(BD1(α)).
定义1.2设A=(aij)∈Cn×n分块如式(1.1).若存在α∈[0,1],使得
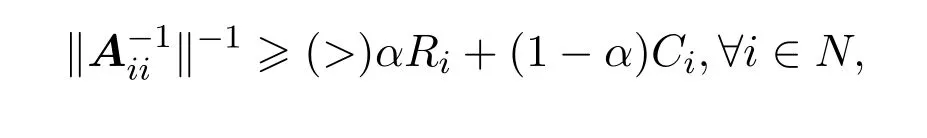
则称矩阵A为块(严格)α2-对角占优矩阵,记为BD2(α0)(BD2(α)).
定义1.3设A=(aij)∈Cn×n分块如式(1.1).若存在α∈[0,1],使得
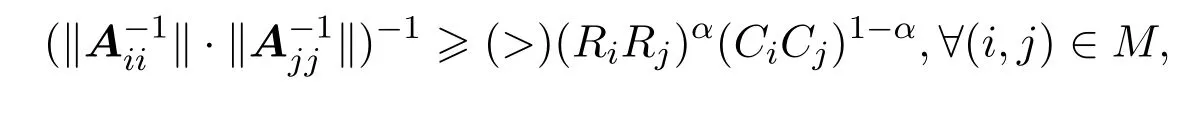
则称矩阵A为块(严格)α1-双对角占优矩阵,记为BDD1(α0)(BDD1(α)).
定义1.4设A=(aij)∈Cn×n分块如式(1.1).若存在α∈[0,1],使得
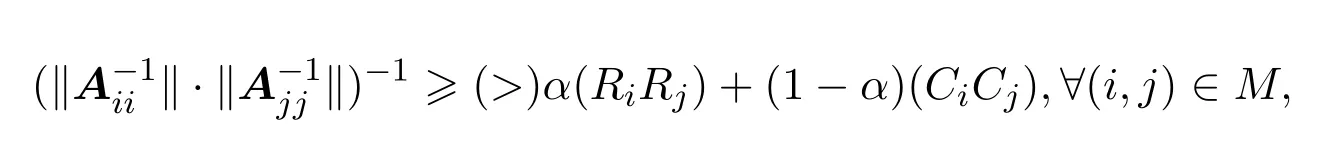
则称矩阵A为块(严格)α2-双对角占优矩阵,记为BDD2(α0)(BDD2(α)).
定义1.5设A=(aij)∈Cn×n分块如式(1.1).若存在α∈[0,1],使得
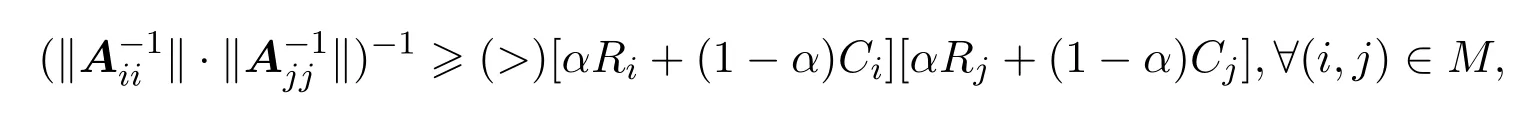
则称矩阵A为块(严格)α3-双对角占优矩阵,记为BDD3(α0)(BDD3(α)).
2 块α-对角占优矩阵定义之间的关系
定理2.1设A=(aij)∈Cn×n分块如式(1.1),则下列结论成立:
1)若A∈BD1(α),则A∈BDD1(α);
2)若A∈BD2(α),则A∈BD1(α),A∈BDD1(α),A∈BDD2(α);
3)若A∈BDD2(α),则A∈BDD1(α);
4)若A∈BDD3(α),则A∈BDD1(α).
定理2.2设A=(aij)∈Cn×n分块如式(1.1),则
1)若A∈BD1(α)时,不蕴含A∈BD2(α),A∈BDD2(α),BDD3(α);
2)若A∈BD2(α)时,不蕴含A∈BDD3(α);
3)若A∈BDD1(α)时,不蕴含A∈BD1(α),A∈BD2(α),A∈BDD2(α),A∈BDD3(α);
4)若A∈BDD2(α)时,不蕴含A∈BD1(α),A∈BD2(α),A∈BDD3(α);
5)若A∈BDD3(α)时,不蕴含A∈BD1(α),A∈BD2(α),A∈BDD2(α).
证明根据定义易知定理2.1和定理2.2的结论是成立的,在此不做详细的证明.
注1定理2.1和定理2.2的结论说明,在所有的块严格α-对角占优矩阵定义中,块严格α1-双对角占优矩阵的条件是最弱的.为此,下面给出块严格α1-双对角占优矩阵的两个等价表征.
3 块严格α1-双对角占优矩阵的等价表征及应用
引理3.1[4]设σ,τ是任意两个非负实数,0≤α≤1,则ατ+(1−α)σ≥τασ1−α.
引理3.2若矩阵A=(aij)∈Cn×n分块如式(1.1),满足下列条件之一:
1)A∈BD1(α);2)A∈BD2(α);3)A∈BDD1(α);
4)A∈BDD2(α);5)A∈BDD3(α).
则A为非奇异的块H矩阵.
证明由文献[5-6]知,在1),3)条件下,结论成立.由引理3.1可知,
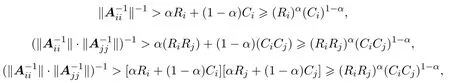
因此,在2),4),5)条件下,结论也成立.
引理3.3设A=(aij)∈Cn×n分块如式(1.1)且M6=∅,如果M1,M2至少有一个空集,则A∈BDD1(α).
证明分三种情况:
情况1
情况2
情况3
因此三种情况下总可得:
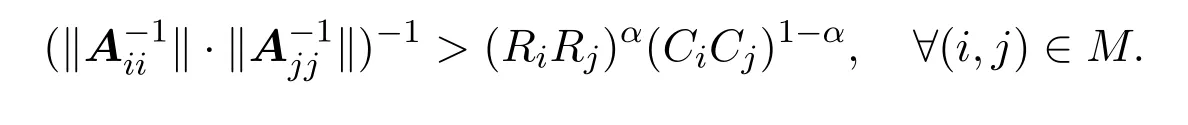
从而根据定义3.1知A∈BDD1(α).
推论3.1设A=(aij)∈Cn×n分块如式(1.1),如果M6=∅,则当M1,M2至少有一个空集时有A为非奇异的块H矩阵.
证明由引理3.2和引理3.3知结论成立.
定理3.1设矩阵A=(aij)∈Cn×n分块形如式(1.1),则A∈BDD1(α)充分必要条件是M6=∅且
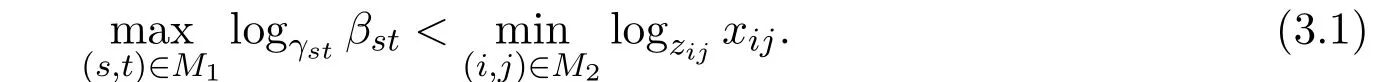
证明充分性由(3.1)式及指标集M1,M2的取法可知,必存在常数α,满足
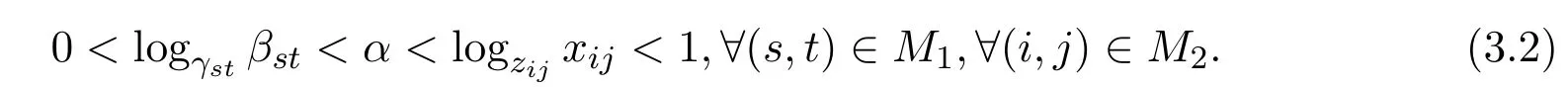
由(3.2)式的第二个不等式,并注意到对任意的(s,t)得
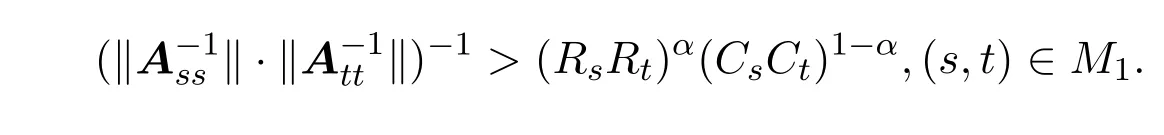
由(3.2) 式的第三个不等式, 注意到对任意的(i; j) ∈ M2; zij = xijyij > 1; 得
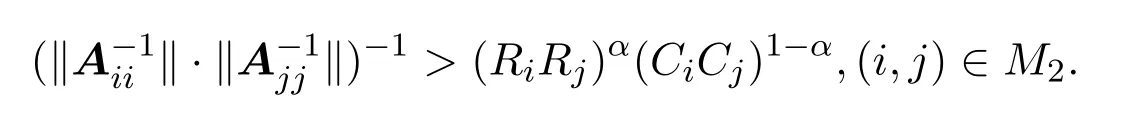
又因为对任意的(i,j)∈∪M4∪M5,α∈(0,1),显然有
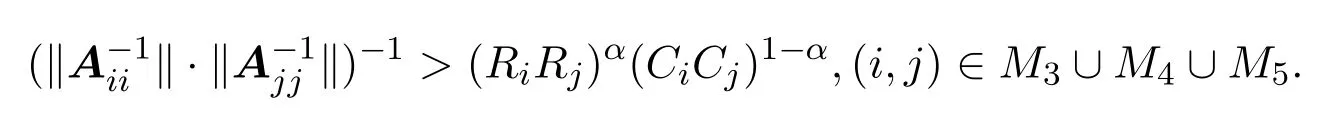
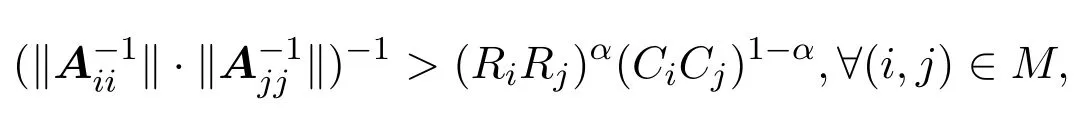
则对任意的(s,t)∈M1,有
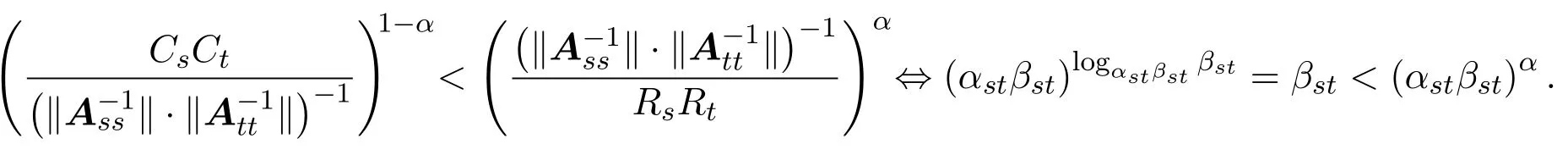
定理3.2设矩阵A=(aij)∈Cn×n分块形如式(1.1),M6=∅,如果矩阵A满足不等式
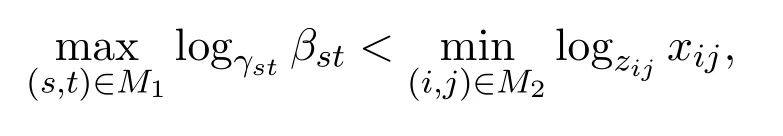
则A为非奇异的块H矩阵.
证明由定理3.1知A∈BDD1(α),再根据引理3.2知,A为非奇异的块H矩阵.
定理3.3设矩阵A=(aij)∈Cn×n分块形如式(1.1),则A∈BDD1(α)充分必要条件是M6=∅且
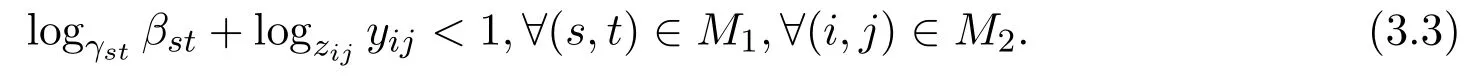
证明充分性由(3.3)式可知,对任意的(s,t)∈M1,(i,j)∈M2有logzijyij<1−logγstβst.由γij>βij>1,得0 令α=logγstβst+ε,得到0<α<1和logγstβst<α,即 在(3.4)式两边同时乘以β−αst,可得 因此对任意的(s,t)∈M1,有 又因为对任意的(l,m)∈M3∪M4∪M5,α∈(0,1),显然有 综上根据定义3.1知A∈BDD1(α). 必要性由定义可知,显然有M6=∅,且存在α∈(0,1),使得 综合可知logγstβst+logzijyij<1,∀(s,t)∈M1,∀(i,j)∈M2.即(3.3)式成立. 定理3.4设矩阵A=(aij)∈Cn×n分块形如式(1.1),M6=∅,如果矩阵A满足不等式: logγstβst+logzijyij<1,∀(s,t)∈M1,∀(i,j)∈M2, 则A为非奇异的块H矩阵. 证明由定理3.3知A∈BDD1(α),再根据引理3.2知,A为非奇异的块H矩阵. 例4.1设矩阵 其中Aij(i,j=1,2,3)均为2×2矩阵.经计算,有 取矩阵范数 经计算,得 即满足定理3.2的条件,所以矩阵A为非奇异的块H矩阵. [1]Huang Tingzhu,Li Wen.Block H-matrices and Spectrum of Block Matrices[J].Applied Mathematics and Mechanics,2002,23(2):236-240. [2]杨鹏,冉瑞生,黄廷祝.非奇块H矩阵的充分条件[J].电子科技大学学报,2004,33(2):204-207. [3]刘建州,徐映红,廖安平.广义块对角占优矩阵的判定[J].高等学校计算数学学报,2005,27(3):250-257. [4]徐成贤,徐宗本.矩阵分析[M].西安:西北工业大学出版社,1991. [5]李庆春,刘磊.矩阵对角占优性的推广[J].吉林师范学院学报,1996,17(5):4-7. [6]高中喜,黄廷祝,刘福体.块H矩阵的简捷判定[J].工程数学学报,2004,21(3):340-344. Discussion for block α-diagonally dominant matrices Gao Huishuang,Han Guichun,Xiao Lixia (School of Mathematics,Inner Mongolia University for the Nationalities,Tongliao028043,China) Applying the theorem of block diagonally dominant matrices,we discuss the relations between block α-diagonally dominant matrices.We give two equivalence representations for strictly double block α1-diagonally dominant matrices.As its application,we obtain some criteria for block H-matrices.In the end,the efficiency of the proposed criteria is showed by a numerical example. block diagonal dominance,block α-diagonally dominant matrices,block H-matrices O151.21 A 1008-5513(2014)01-0053-07 10.3969/j.issn.1008-5513.2014.01.009 2013-11-21. 内蒙古民族大学科学研究基金(NMD1226). 高会双(1980-),硕士,讲师,研究方向:数值代数和算子代数. 2010 MSC:15A57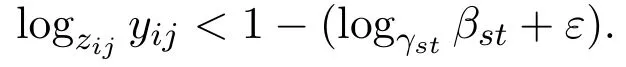


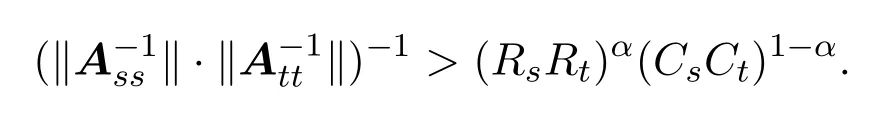
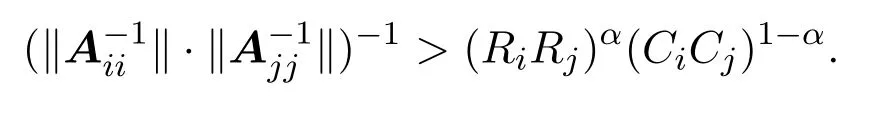
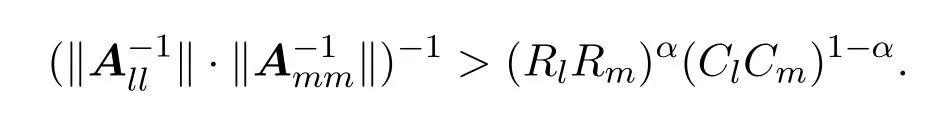
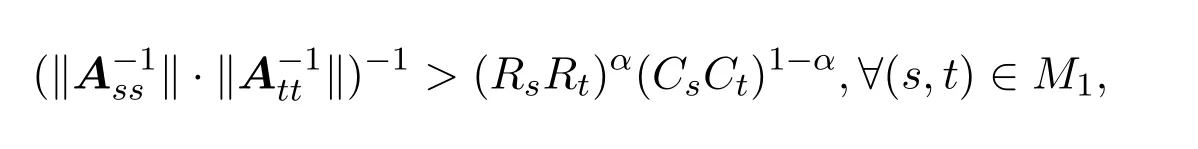
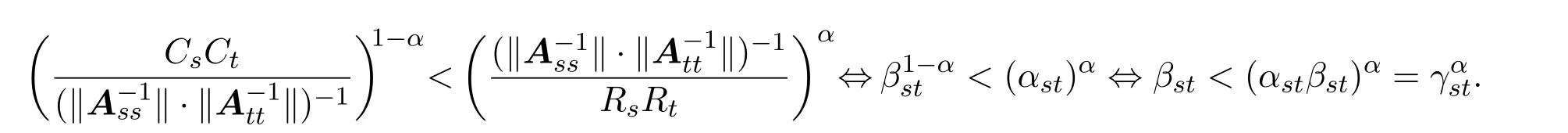
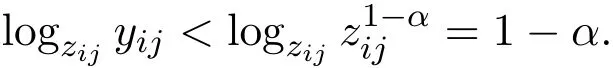
4 数值例子