基于完备序列集的扩频码构造方法

吴成茂, 张晓蓉, 王 辉, 方鹏飞, 魏兵阳

(1. 西安邮电大学 电子工程学院, 陕西 西安 710121；2. 西安邮电大学 自动化学院, 陕西 西安 710121;3. 西部机场集团有限公司， 陕西 西安 710075)

基于完备序列集的扩频码构造方法

吴成茂1, 张晓蓉1, 王 辉2, 方鹏飞3, 魏兵阳1

(1. 西安邮电大学 电子工程学院, 陕西 西安 710121；2. 西安邮电大学 自动化学院, 陕西 西安 710121;3. 西部机场集团有限公司， 陕西 西安 710075)

为了改善传统扩频序列周期短、复杂度低的问题，提出一种基于完备序列集的扩频码构造方法。利用移位算法将二进制理想的二元自相关序列转换为长周期、高复杂度的完备序列集，随机地按行或列抽取完备序列集中的子序列，以其作为扩频码并用于扩频通信。利用传统伪随机序列和Logistic混沌序列分析该方法的有效性，并与现有方法相比得知，新方法可改善序列相关性，提高序列复杂度。仿真测试结果显示，完备序列具有较强的抗噪声干扰能力，并能获得较低的扩频误码率。

二元理想自相关序列；完备序列集；伪随机序列；Logistic混沌序列；误码率

在当今电磁环境越来越恶劣的情况下，扩频通信技术可以大大提高通信系统的抗干扰性能。扩频技术不仅在军事通信中发挥着不可取代的优势，而且已广泛渗透到了通信的各个方面，如移动通信、卫星通信、微波通信、无线定位系统、无线局域网和全球个人通信等[1]。

产生高质量的扩频码序列是扩频通信系统最关键的问题之一。传统m序列是应用最广泛的一种扩频码，但因采用线性移位寄存器，故具有周期短、互相关性差、码组数目有限以及序列复杂度低等缺陷[2]，采用累积检测法易于侦破且难以满足多址通信中地址码的要求。Gold码序列是基于m序列的一种改进拟正交码序列，虽有良好周期自相关性和互相关性，但码数量依然有限,且周期短易被复制和侦查，故其扩频通信保密性仍然较差[3]。为克服经典扩频码的上述不足，类Gold序列、Walsh序列、双重BCH序列、Kasami序列、Bent序列、Baker序列、Williad序列和Neuman-Hofman序列等被引入扩频通信[4]。为了改善序列复杂度，一些具有低相关性的序列集被提出，如Gold序列集[5]、Bent序列集[6]和广义Kasami序列集[7]，但是它们的线性复杂度依然很低。完备序列集的提出[8-9]，最早是由几乎完备序列集通过改进后产生的，但是这种序列集具有较低的自相关程度和互相关程度以及周期短等缺陷。

针对以上情形，本文将引用移位算法获得周期较长、复杂度较高的完备序列集，然后根据抽样原理对该序列集进行抽样，产生性能优良的扩频码序列，并将新序列与现有扩频码序列的性能进行分析比较。

1 新的扩频码构造方法

以二元理想自相关序列[10]为基础构造周期较长、复杂度较高的完备序列集，然后引用抽样原理，对完备序列集进行随机按行或列抽样，将所得高性能序列作为扩频码，应用于扩频通信系统中。

具体算法如下。

步骤1 构造以

N=2n-1(n∈),

为周期的二元理想自相关序列[9]

s=“s0，s1，…，sN-1，…”。

步骤2 记取

N={k:k∈,0≤k≤N-1},

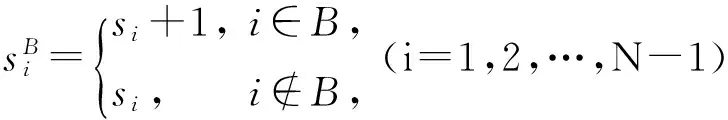
步骤3 选取r<(N-1)/4,以使B中元素的个数不超过r，得到完备序列集

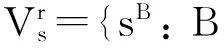
其中sB为以N为周期的二元序列，即

步骤4 引用抽样原理，将步骤3产生的完备序列集按行(列)随机抽样得到的随机序列作为扩频码应用于扩频通信系统中。

如取N=31,r=1,二元理想自相关序列

s=“1,1,1,1,1,0,0,1,1,0,1,0,0,1,0,0,

0,0,1,0,1,0,1,1,1,0,1,1,0,0,0,…”，

则可得完备序列集

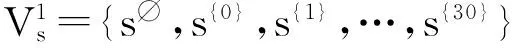
其中

s∅=“1,1,1,1,1,0,0,1,1,0,1,0,0,1,0,0,

0,0,1,0,1,0,1,1,1,0,1,1,0,0,0,…”,

s{0}=“0,1,1,1,1,0,0,1,1,0,1,0,0,1,0,0,

0,0,1,0,1,0,1,1,1,0,1,1,0,0,0,…”,

s{1}=“1,0,1,1,1,0,0,1,1,0,1,0,0,1,0,0,

0,0,1,0,1,0,1,1,1,0,1,1,0,0,0,…”

………………,

s{30}=“0,1,1,1,1,0,0,1,1,0,1,0,0,1,0,0,

0,0,1,0,1,0,1,1,1,0,1,1,0,0,1,…”，

2 扩频码的特性分析

主要分析扩频码序列的相关性和复杂性。

2.1 相关性分析

在扩频通信中，相关性是衡量扩频序列特性的一个重要技术指标，即扩频码序列相关性的好坏与扩频通信系统的抗多径干扰能力有着直接影响。设二值随机序列的周期为N,则该二值序列s的自相关系数定义为[10]

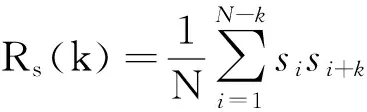
序列s和t的互相关系数定义为

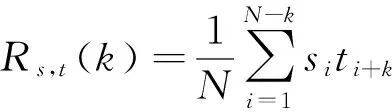
其中k为步长参数。相关系数的值与步长k有关，当步长增加时，如果相关系数减小，说明对应二値随机序列的随机性越好。

各种随机序列的相关性测试结果如图1至图4所示，可见新扩频码序列的相关性相对于传统伪随机序列和混沌随机序列的相关性较好，其自相关峰非常尖锐,且旁瓣很小，几乎为0，说明其自相关性很强。互相关值在零附近扰动。由此可说明新构造的扩频码序列有良好的相关性能。

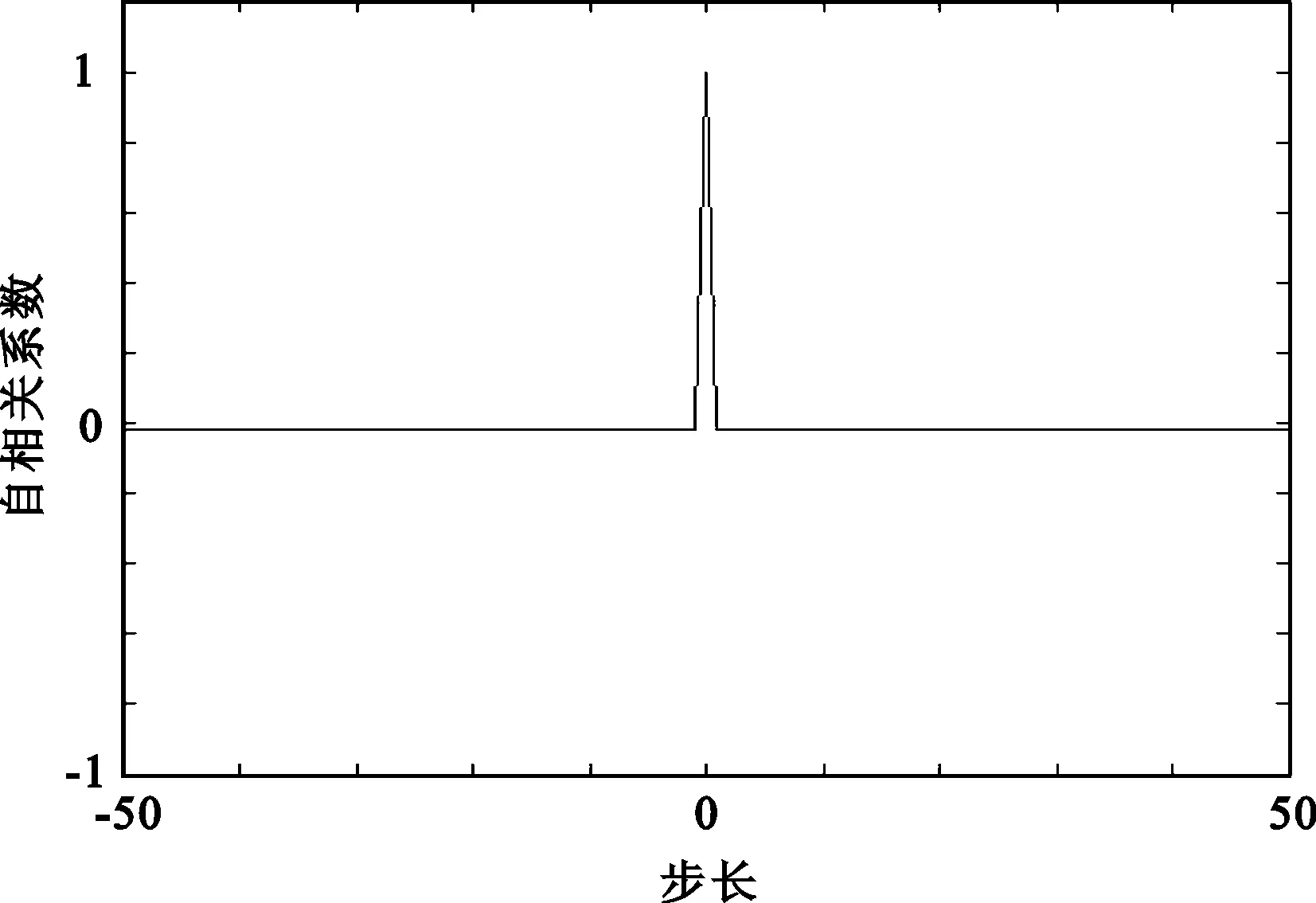
(a) 自相关性

(b) 互相关性

(a) 自相关性

(b) 互相关性

(a) 自相关性

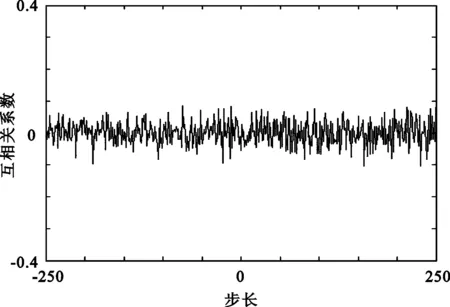
(b) 互相关性

为了进一步了解各种随机序列的自相关和互相关特性，取序列长度为1 000的随机序列，求其自相关和互相关的最大值、最小值，其详细情况如表1所示，其中自相关的最大值是除去1之外的最大值。

表1 不同扩频码序列的自相关和互相关值

从表1所示的自相关和互相关的最大值和最小值来看，新的扩频码序列相关特性较为稳定，且波动更小，能满足扩频通信和图像加密等众多领域应用需要。

2.2 复杂度分析

复杂度对提高扩频通信系统安全性具有重要意义，也是判断扩频序列安全性的重要指标之一。由于信号经常会受到突发干扰而出现异常数据，而近似熵具有较好的鲁棒性，对实测信号的分析很有利,所以可考虑用来分析不同随机序列的复杂度。定义近似熵

H=Φw(e)-Φw+1(e)=

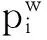
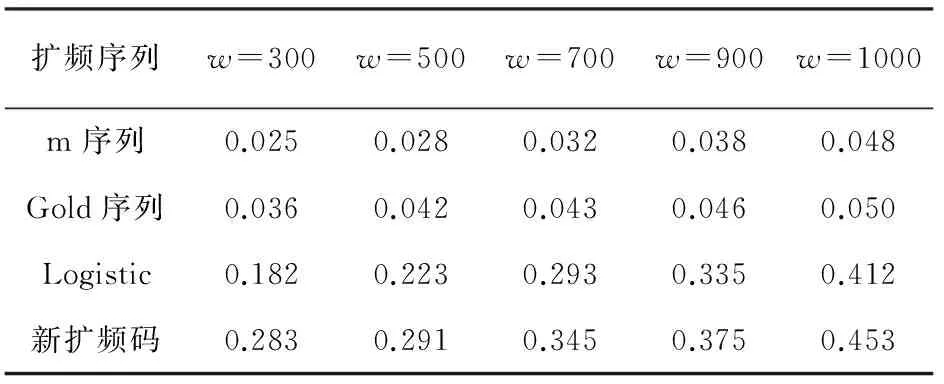
表2 不同随机序列的近似熵比较

从表2中可知，传统m序列和Gold的复杂度值很小，说明它们的复杂度很低，而新构造的扩频码序列的近似熵值相对较大，说明其复杂度较高。亦说明了该扩频码序列应用于扩频通信信息传输是可行的，其高复杂性满足通信系统抗干扰、抗侦破的要求，能够保证信息高安全保密传输。

3 扩频通信仿真分析

为了进一步验证通过移位算法和抽样算法得到的新随机序列作为扩频码所具有的良好特性，通过蒙特卡罗仿真模型，分别将传统伪随机序列、Logistic混沌序列和新随机序列作为扩频码，应用于扩频通信系统，进行仿真分析。

在不同信噪比条件下进行误码率性能分析，通过仿真计算并将其误码率同现有的扩频码序列的通信误码率进行比较，结果证明新产生的扩频码序列的扩频通信误码率性能在某些方面要优于现有扩频通信误码率性能。

在仿真过程中，采用的信道干扰是高斯白噪声(σ2=N/2)和正弦干扰i(n)=Asin (n)(A<31)的叠加。每次仿真中，在不同的信噪比下，发射端都产生1 000 bit的信息数据,由发射端序列扩频，经过有高斯白噪声和正弦干扰的信道，其正弦干扰信号可以分别给定为不同幅值。

图5至图8分别是对不同扩频码序列进行误码率性能仿真的结果。图中4条曲线由上而下分别代表正弦干扰幅值A为12，7，3，0。

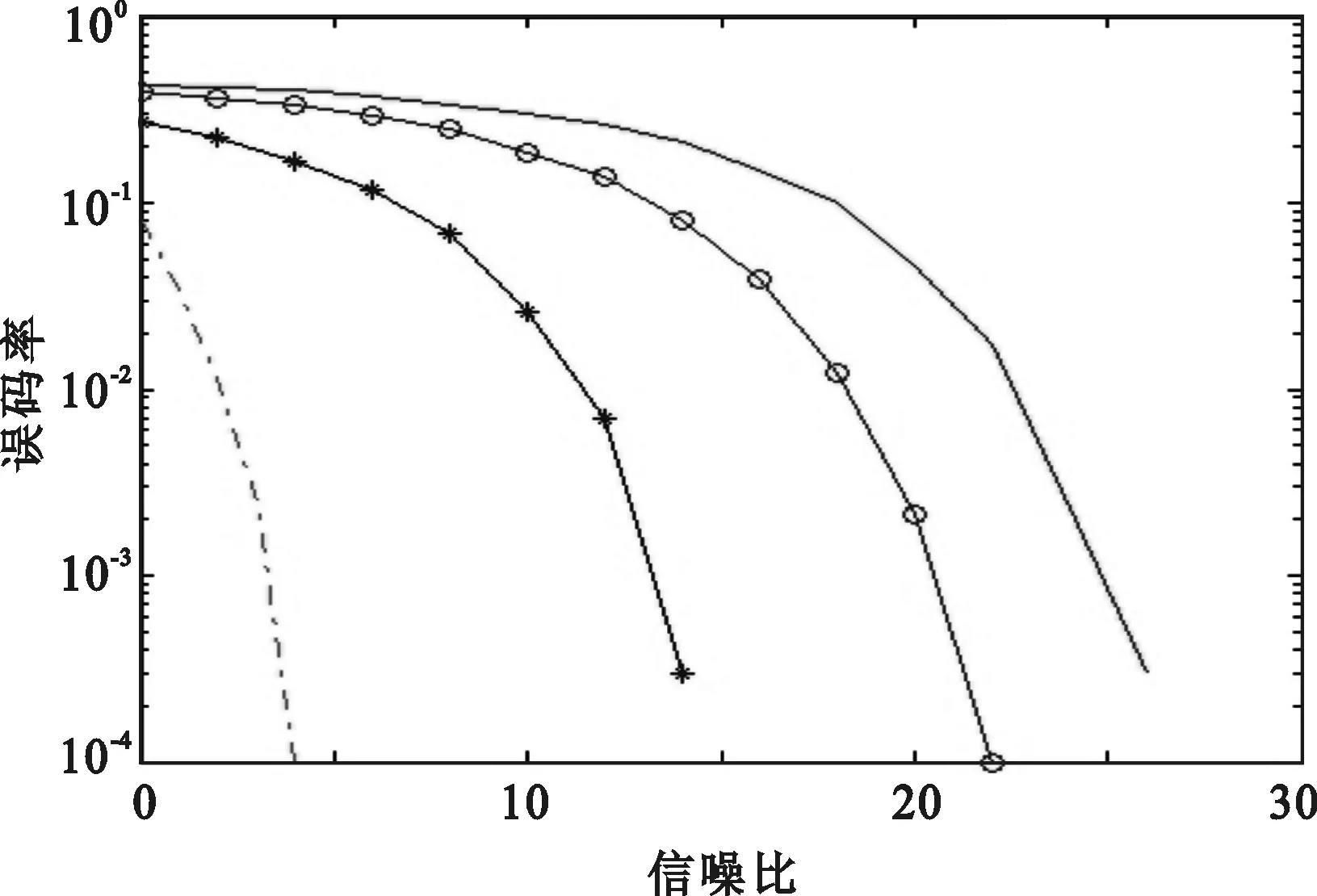
图5 m扩频序列在不同幅度下的误码率

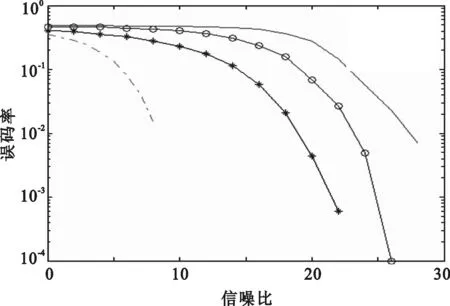
图6 Gold扩频序列在不同幅度下的误码率

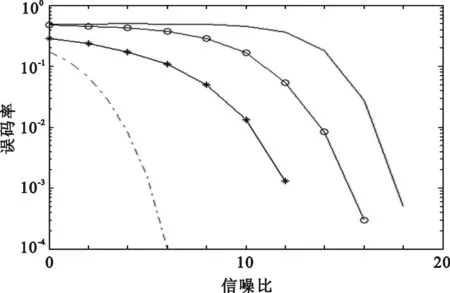
图7 Logistic扩频序列在不同幅度下的误码率

图8 复合扩频序列在不同幅度下的误码率

从随机序列误码率曲线可知，新扩频序列的误码率曲线较m序列、Gold以及Logistic混沌序列作为扩频序列的误码率曲线稍微平滑一些，在正弦干扰幅度值A=0的情况下，m序列、Gold序列和Logistic混沌序列的误码率相比新扩频码序列的误码率较低，而其它三者的误码率大致相当；这说明了其他三种扩频序列的抗噪声干扰能力较差。当正弦干扰幅值加大时，新随机序列作为扩频码的通信误码率曲线下降的更快一点，这说明新扩频码序列在大幅值干扰下具有较好的抗噪声干扰能力。

将不同随机序列作为扩频码应用到单用户扩频系统，其误码率测试结果如表3至6所示。

表3 m序列扩频通信系统误码率

表4 Gold序列扩频通信系统误码率

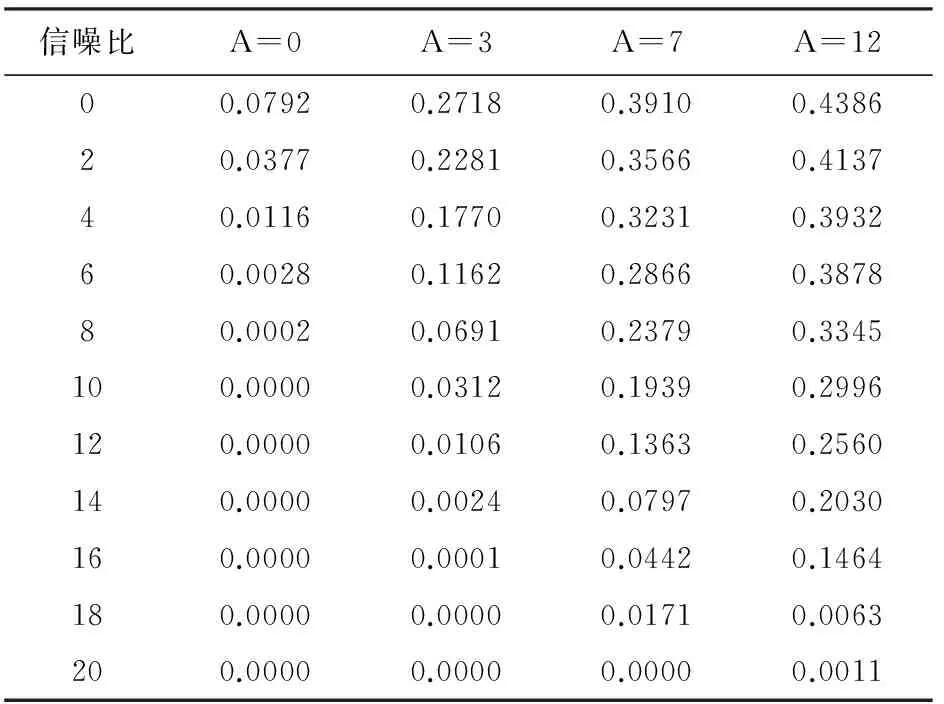
表5 Logistic混沌序列扩频通信系统误码率

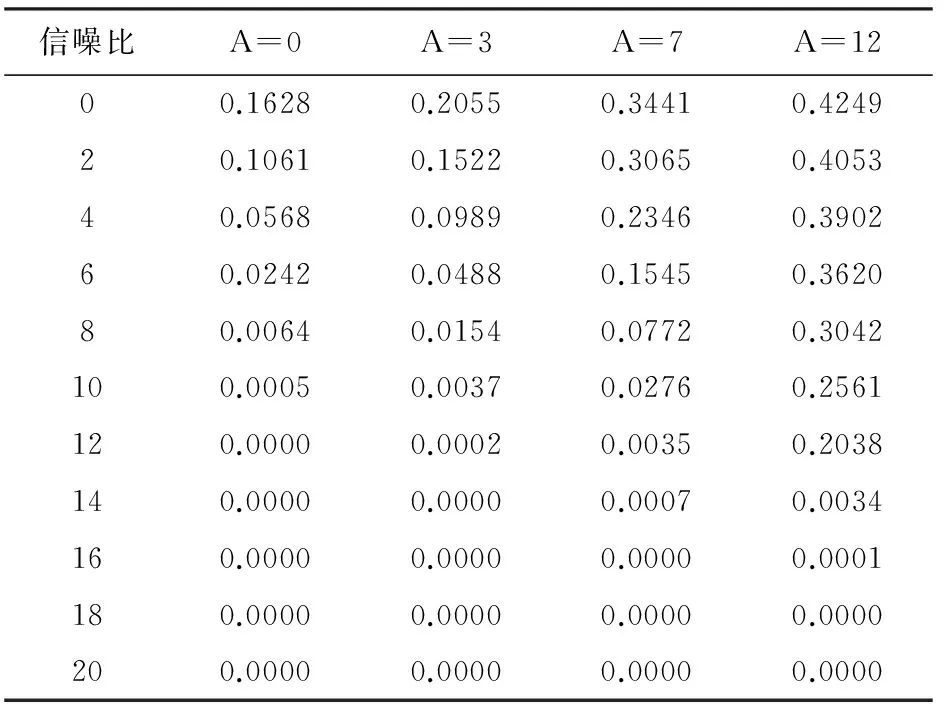
表6 新扩频码序列扩频通信系统误码率

对比分析不同随机序列作为扩频码的误码率，可以发现，基于完备序列集所产生的新随机序列作为扩频码能获得较低的误码率。

(1) 信道信噪比对系统误码率的影响

当幅度一定的情况下，信噪比取值在0～20 dB变化时,新随机序列在扩频通信系统的误码率明显低于m序列、Gold序列和Logistic扩频序列的误码率。在幅度不变时，随着信噪比的增大，其误码率逐渐降低，特别是新扩频码序列对应误码率降低更显著，能够适应码分多址扩频通信的需要。

(2) 干扰幅度对系统误码率的影响

测试中干扰幅度值分别取0、3、7、12，当信噪比一定时,随着幅度的增加,其误码率增大，但从整体上来看，新随机序列扩频码的通信误码率相对其它扩频序列的误码率较低。当幅度A=0时，新扩频码序列的误码率较其它三种扩频序列的误码率高，但是随着幅度值的增大新扩频序列的误码率较其它三种扩频序列的误码率低，说明新构造的扩频码应用扩频通信系统的抗噪声干扰能力强于其它扩频序列，并且其性能更优越，具有良好的抗噪能力和抗多址干扰能力，能获得较低误码率。

4 结论

通过移位算法和抽样算法得到的新扩频码序列的相关性好，周期长，复杂度高，既可增加预测难度，又能提高保密性。仿真测试表明，采用新构造的新扩频码序列的抗噪声干扰能力较好，相比传统方法更为优越，并且可以很好地解决扩频通信系统中的信道干扰问题，保证信号传输的准确率，提高了扩频通信系统的可靠性和安全性。

[1] 黄乘顺,李星亮.基于混沌的扩频通信系统及性能分析[J].通信技术,2008,41(12):37-39.

[2] Hill P C J, Ridley M E. Blind estimation of direct-sequence spread spectrum m-sequence chip codes[C]//2000 IEEE Sixth International Symposium on Spread Sprectrum Techniques and Applications. NJ Parsippany:IEEE, 2000:305-309.

[3] Pursley M B, Sarwate D V. Performance evaluatio n for phased-coded spread-spectrum multiple access communication: Part11:Code sequence analysis[J].IEEE Transactions on Communications,1977,25 (8):800-803.

[4] Jack K H. Spread Spectrums for GNSS and Wireless communications[M].BeiJing: Publishing House of Electronics Indurstry, 2013:15-40.

[5] Gold R. Maximal recursive sequences with 3-valued recursive cross-correlation functions[J]. IEEE Transactions on Information Theory,1968,14(1):154-156.

[6] Olseb J D, Scholtz R A, Welch L R. Bent function sequences[J]. IEEE Transactions on Information Theory, 1982,28(6):858-864.

[7] Zeng Xiangyong, Hu Lei, Liu J Q, et al. On the linear span of a binary sequence family with optimal correlation properties[J]. IEICE Transactions on Fundamentals, 2008, 91(2):664-672.

[8] Cai Kai, Weng Guobiao, Cheng Xueqi. Binary almost perfect sequence sets[J]. IEEE Transactions on Information Theory,2010,56(7):3594-3604.

[9] Xiong Hai,Qu Longjiang, Li Chao. New construction of perfect sequence set and low correlation zone sequence set[J]. Science China: Information Sciences,2013,56(11):1-8.

[10] 吴成茂,李杜娟,王保平.混沌扩频通信及其误码率[J].西安邮电大学学报,2013,18(3):10-13.

[责任编辑:瑞金]

Constructing spread-spectrum code based on perfect sequence set

WU Chengmao1, ZHANG Xiaorong1, WANG Hui2, FANG Pengfei3, WEI Bingyang1

(1.School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China；2. School of Automation, Xi’an University of Posts and Telecommunications, Xi’an 710121, China;3. China West Airport Group, Xi’an 710075, China)

In order to solve the problem of short period and low-complexity in traditional spread spectrum sequence, a method of constructing spread-sprectrum code based on perfect sequence set is proposed in this paper. In this method firstly a perfect sequence set of long period and high complexity is obtained by using binary ideal autocorrelation sequence through the algorithm of shift. A spread spectrum code is then set by random sampling row or column sub-sequence of perfect sequence and used for spread spectrum communication. The effectiveness of this method is analysed based on traditional pseudo-random sequence and Logistic chaos sequence. Compared with the conventional method, this method can improve correlation of sequence and increase complexity of sequence. Simulation test show that the perfect sequence has strong noise immunity, and can also obtain a lower spread bit error rate.

two-level ideal autocorrelation sequence, perfect sequence set, pseudo-random sequence, Logistic chaotic sequence, bit error rate

10.13682/j.issn.2095-6533.2014.06.007

2014-05-20

国家自然科学基金重点资助项目(90607008)；国家自然科学基金资助项目(61073106)；陕西省自然科学基金资助项目(2014JM8331,2014JQ5183,2014JM8307);陕西省教育厅科学研究计划资助项目(2013JK1129)

吴成茂(1968-)，男，高级工程师，从事数字图像处理研究。E-mail:wuchengmao123@sohu.com 张晓蓉(1989-)，女，硕士研究生，研究方向为扩频通信。E-mail:971401590@qq.com

TN914.42

A

2095-6533(2014)06-0032-06