一类混沌系统的输入状态稳定控制器设计

范永青, 刘 瑾

(西安邮电大学 自动化学院, 陕西 西安 710121)

一类混沌系统的输入状态稳定控制器设计

范永青, 刘 瑾

(西安邮电大学 自动化学院, 陕西 西安 710121)

针对一类混沌系统中平衡点不稳定的问题，提出一种新型自适应控制器的设计方法。该方法基于输入到状态稳定性理论及小增益定理，采用线性反馈控制与非线性自适应控制相结合的设计思想，在所设计线性反馈增益满足一定取值条件，且非线性控制器部分中的参数满足所设计的自适应律时，使得一类混沌系统的所有平衡点快速实现全局渐进稳定。算例数值仿真验证了该设计方法的有效性。

混沌系统；自适应控制；输入状态稳定；全局渐进稳定

混沌现象广泛存在于许多实际工程系统中[1]。近年来，如何控制或利用混沌现象已经成为非线性系统研究的一个热点[2]。由于混沌系统对系统的初始值具有较强的敏感性[3]，因此，如何控制混沌系统平衡点的稳定性是一个值得研究的问题。混沌系统可看作是非线性系统的一种特例，对混沌系统控制亦可借鉴非线性系统的控制方法去研究。当考虑非线性系统的全局性质时，系统的输入-输出稳定优于系统的Lyapunov稳定，所以系统的有界输入-有界输出和系统的输入-状态稳定(Input-to-state stability，ISS)十分相似[4-5]。有关非线性系统输入-状态稳定的研究受到了众多学者的青睐，并涌现出大量的科研成果[6-11]。这些成果为具有混沌现象的非线性系统稳定性研究提供了新的思路与方法。

由于ISS系统本身具有一个特征，即当不考虑系统的初始状态时，只要输入量小，那么系统的状态最终必定是小的[4]。根据这一特征，得出ISS系统是全局渐进稳定的结论。如果采用ISS系统的控制器设计思想，对混沌系统的平衡点设计使其稳定的控制器，则混沌系统的平衡点镇定问题就不会因为初始值的敏感而影响控制器的设计。

鉴于以上分析ISS系统的优点，本文采用ISS控制器设计方法，对一类混沌系统的平衡点全局稳定性问题，基于输入到状态稳定和小增益定理，提出一种简单的反馈自适应控制器设计方法。

1 问题概述

设非线性动力系统

(1)

其中x∈n为系统的状态变量，u∈m为控制输入，且u:[0,∞)→m为分段连续有界函数，其范数为

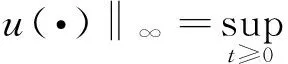
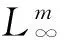
‖x(t)‖≤

max{β(‖x0‖,t),γ(‖u(·)‖∞)},

(2)

则式(1)是输入状态稳定的，函数γ(·)称为增益函数。

(3)

‖x‖≥χ(‖u‖)⟹

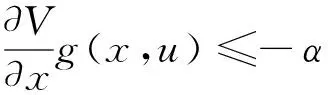
(4)

成立，则称V(·)为式(1)的一个ISS-Lyapunov函数。

‖x(·)‖∞≤

max{γ0(‖x0‖),γ(‖u(·)‖∞)},

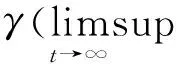
(5)

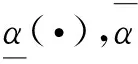
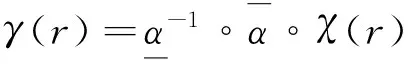
(6)

定理2(小增益定理)[12]如果γ1(γ2(r))0都成立，则把x=(x1,x2)看作状态变量，把u看作输入变量时，式(1)是ISS稳定的。

考虑混沌系统为

(7)

其中a>0,b>0,c>0为控制参数，式(7)有5个平衡点，分别为

E0=(0,0,0),

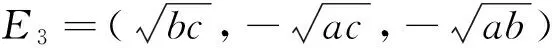
(8)

对式(7)实施控制作用，经过坐标变换后为

(9)

由此设计的自适应控制器u=(u1,u2,u3)T,可使式(7)在平衡点是全局渐进稳定。

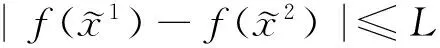
2 ISS控制器设计

设计控制器

(10)

其中

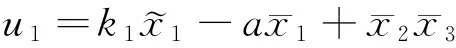
参数k1,k2为待设计的参数。参数调节律为

(11)

其中λ>0，且

(12)

参数θ,λ,δ,ε为设计的正实数。

针对式(7)的平衡点不稳定问题，给出主要结论及证明。

定理3 在控制器式(10)和自适应律式(11)、式(12)的控制作用下，当假设1成立且控制增益参数满足

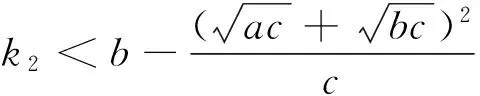
存在足够小的正数σ满足条件

c1=c-2σ,

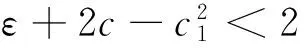
则式(9)在原点是全局渐进稳定的。

证明 针对控制任务，分两种情形。

‖。

容易验证此情形满足s>0。考虑关于s的正定函数

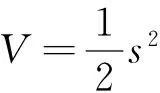
采用开环控制，则V沿式(9)的轨道导数为

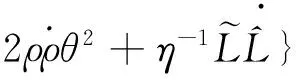
(13)

由定理3，则成立不等式

(14)

式(14)意味着式(9)的状态能够在有限时间内到达曲面s=0[13]。

(15)

(16)

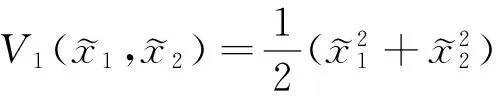
(17)

V1沿式(16)的导数为

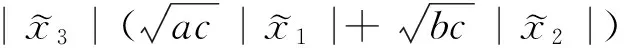
(18)

则有不等式

(19)

由式(18)和式(19)可知

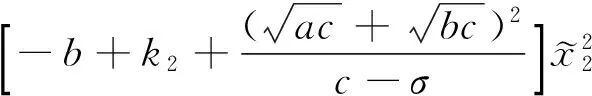
(20)

若控制增益参数满足

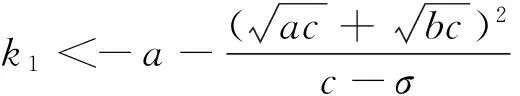
则可以找到足够小的正数σ，对于某一正数μ，满足不等式

(21)

由式(20)和式(21)可知，成立不等式

(22)

K∞函数取为

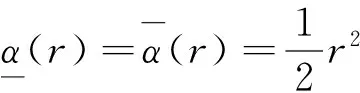
α(r)=μr2,

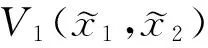
考虑第二个子系统

(23)

(24)

式(24)沿式(23)的导数为

(25)

由自适应律式(11)和式(12)可知，成立不等式

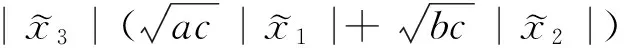
(26)

因为有不等式

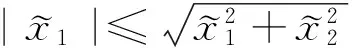
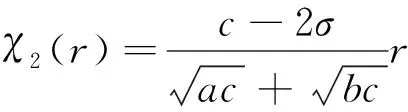
成立时，则有不等式

(27)

(28)

由不等式式(26)，式(28)可得

(29)

记c1=c-2σ，因为

(30)

由式(29)和式(30)，可得

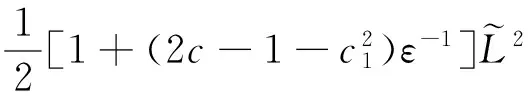
(31)

在式(31)中，由定理3中的条件

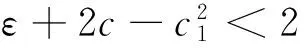
则有

(32)

取K∞函数为

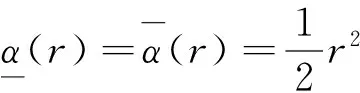
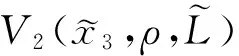
由式(6)可知，增益函数的复合函数为

(33)

从式(33)中可以看出，增益函数的复合函数是一个压缩映射，因此式(15)是ISS稳定的, 其原点是全局渐进稳定的。

3 仿真算例

对受控系统式(9)，由定理3中的控制增益k1，k2参数需要满足的取值条件，取参数

k1=-40,k2=-25,

系统的初始状态为

自适应参数初始值取为

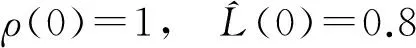
自适应律式(11)，式(12)中的参数为

θ=20,λ=200,

δ=0.05,ε=0.001。

根据系统的参数取两组值分别讨论其平衡点的稳定性。

实验1 令式(9)中的参数取值为

a=4.5, b=12, c=5。

系统的5个平衡点分别为

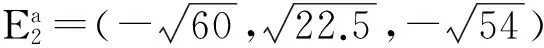
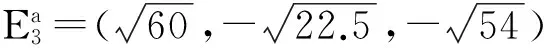
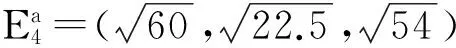
对平衡点实施控制时，系统状态的变化情况分别如图1至图5所示。

实验2 令式(9)中的参数取值为

a=0.4, b=12, c=5。

系统的5个平衡点分别为

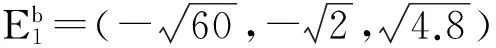
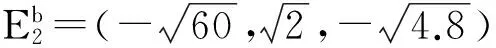
对平衡点实施控制时，系统状态的变化情况分别如图6至图10所示。

从参数取两组情形的仿真结果可以看出，系统的所有平衡点可以在自适应控制器式(10)、式(11)和式 (12)的控制作用下，很好地到达稳定状态，且控制器中自适应参数是一致有界的。

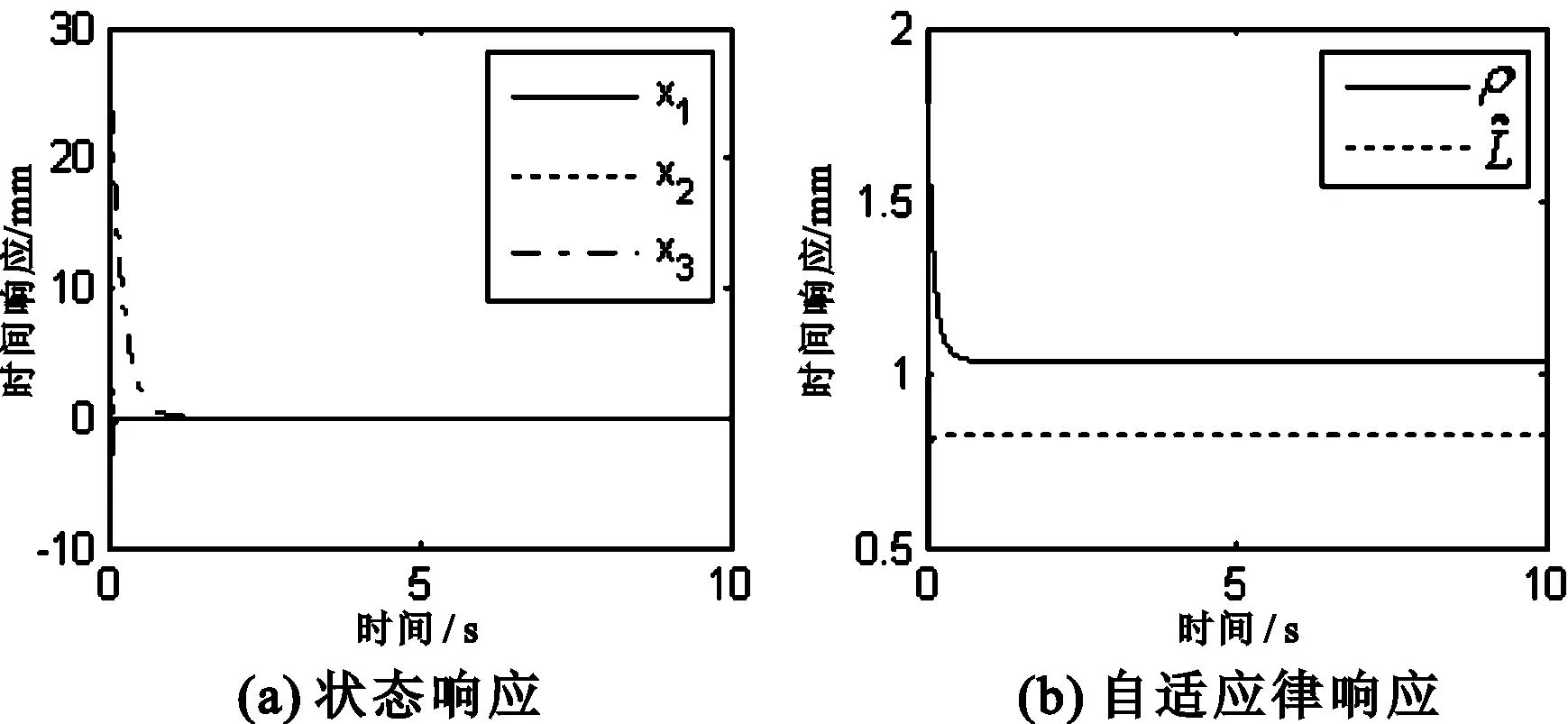
图1 平衡点的状态响应与自适应律的时间响应

图2 平衡点的状态响应与自适应律的时间响应

图3 平衡点的状态响应与自适应律的时间响应

图4 平衡点的状态响应与自适应律的时间响应

图5 平衡点的状态响应与自适应律的时间响应

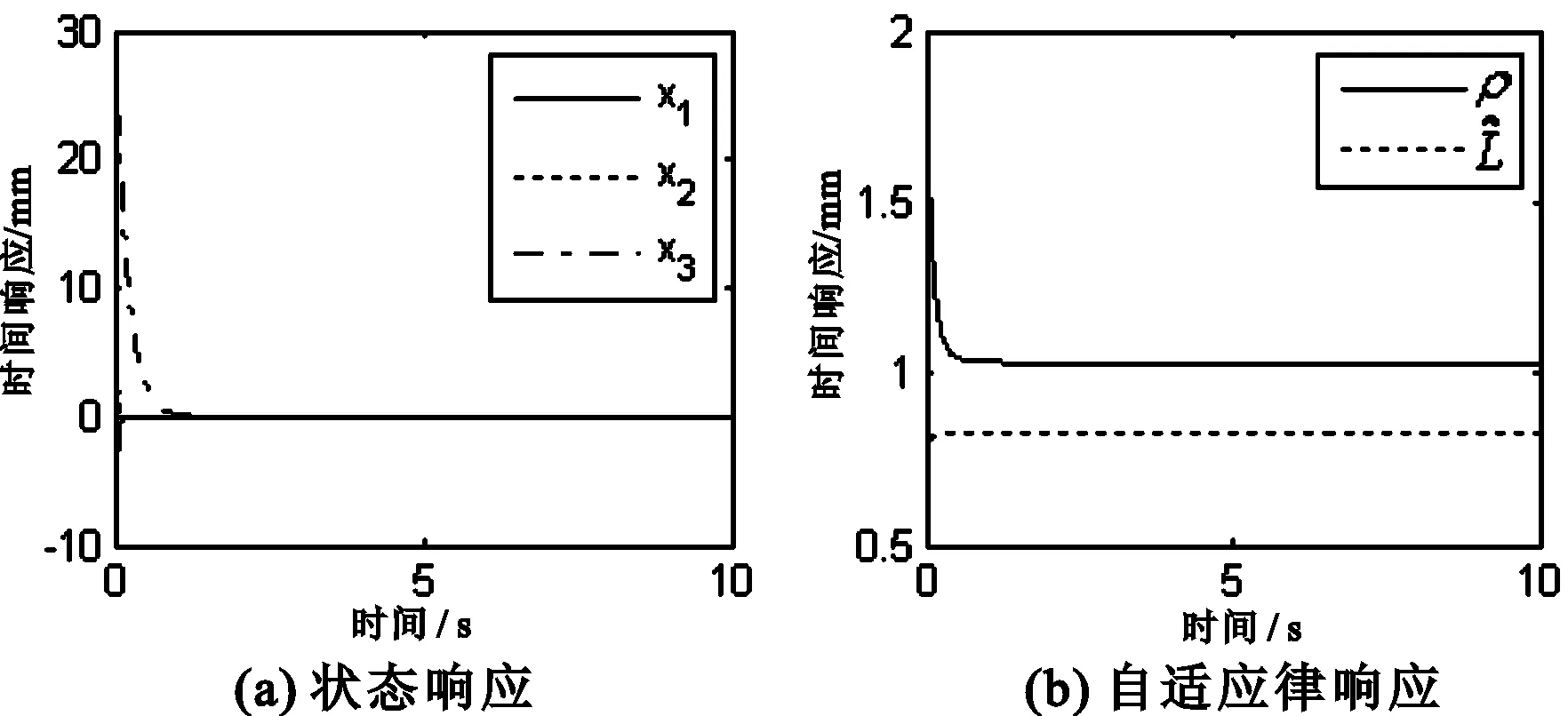
图6 平衡点的状态响应与自适应律的时间响应

图7 平衡点的状态响应与自适应律的时间响应

图8 平衡点的状态响应与自适应律的时间响应

图9 平衡点的状态响应与自适应律的时间响应

图10 平衡点的状态响应与自适应律的时间响应

4 结论

研究了一类混沌系统的平衡点镇定问题，利用ISS系统和小增益定理，提出一种状态反馈自适应控制器设计方案，该设计方法避免了其它控制器设计中由于初值的敏感性所导致的控制器设计困难的问题。通过理论分析，证明了闭环系统中的所有信号都是全局稳定的。

[1]PikovskyA,RoseblumM,KurthsJ.Synchronization:AUniversalConceptinNonlinearSciences[M].NewYork:CambridgeUniversityPress, 2003： 1-24.

[2]HüblerA,LüscherE.Resonantstimulationandcontrolofnonlinearoscillators[J].Naturwissenschaften, 1989, 76(2): 67-69.

[3]FarmerJD,Sensitivedependenceonparametersinnonlineardynamics[J].PhysicsReviewLetter, 1985, 55(4): 351-354.

[4] 范子彦, 韩正之. 非线性控制系统的输入:状态稳定性及有关问题[J]. 控制理论与应用, 2001, 18(4): 473-477.

[5]SontagED.Smoothstabilizationimpliescoprimefactorization[J].IEEETrans.onAutomaticControl, 1989, 34(4): 435-443.

[6]TsiniasJ.Stochasticinput-to-statestabilityandapplicationstoglobalfeedbackstabilization[J].InternationalJournalofControl, 1998, 7(5): 907-930.

[7]YangYansheng,ZhouChangjun.Adaptivefuzzystabilizationforstrict-feedbackcanonicalnonlinearsystemsviabacksteppingandsmall-gainapproach[J].IEEETrans.onFuzzySystems, 2005, 13(1): 104-114.

[8]ArcakM,TeelA.Input-to-statestabilityforaclassofLuriesystems[J].Automatica, 2002, 38(11): 1945-1949.

[9]FridmanE,DambrineM,YeganegarN.Oninput-to-statestabilityofsystemswithtime-delay:Amatrixinequalitiesapproach[J].Automatica, 2008, 44(9): 2364-2369.

[10] 段纳, 王璐, 赵从然. 一类具有积分输入到状态稳定未建模动态的高阶非线性系统的状态反馈调节[J]. 控制理论与应用, 2011, 28(5): 639-644.

[11]ChenWuhua,ZhengWeixing.Input-to-statestabilityfornetworkedcontrolsystemsviaanimprovedimpulsivesystemapproach[J].Automatica, 2011, 47(4): 789-796.

[12]IsidoriA.Nonlinearcontrolsystems[M].London:Springer-Verlag，1999：143-146.

[13]SlotineJJE,LiW.应用非线性控制[M]. 程代展,译.北京：机械工业出版社,2006：186-191.

[责任编辑:祝剑]

Stabilization control design of input-to-state stability for a class of chaotic systems

FAN Yongqing, LIU Jin

(School of Automation, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

A new adaptive controller method is proposed for unstable equilibria of a class of chaotic systems. The method is designed by using linear feedback control combining with nonlinear adaptive control, and based on input-to-state stability and small-gain theorem. When the linear feedback control gain is satisfied at certain condition, and some parameters in the nonlinear control are satisfied with adaptive laws, the all equilibria are globally asymptotically stable by employing the proposed controller. The design and analysis are validated by numerical simulation.

chaotic system, adaptive control, ISS(Input-to-state stability), globally asymptotically stability

10.13682/j.issn.2095-6533.2014.06.017

2014-05-13

国家自然科学基金资助项目(61305098);陕西省教育厅科学研究计划资助项目(2013JK0197,14JK1671);西安邮电大学青年教师科研基金资助项目(ZL2013-32)

范永青(1978-)，女，博士，讲师，从事非线性系统控制研究。E-mail: fanyonqqing@xupt.edu.cn 刘瑾(1978-),女，硕士，讲师，从事教育管理研究。E-mail:Liuj@xupt.edu.cn

TP273

A

2095-6533(2014)06-0086-06