基于遗传算法的铣削参数优化*

吴 玲,左健民,王保升,汪木兰

(1.常州大学 机械工程学院,江苏 常州 213016; 2.江苏理工学院,江苏 常州 213001; 3.南京工程学院 先进数控技术江苏省高校重点建设实验室,南京 211167)

基于遗传算法的铣削参数优化*

吴 玲1,左健民2,王保升3,汪木兰3

(1.常州大学 机械工程学院,江苏 常州 213016; 2.江苏理工学院,江苏 常州 213001; 3.南京工程学院 先进数控技术江苏省高校重点建设实验室,南京 211167)

为了科学选取铣削用量,提高生产效率、降低生产成本。利用试验数据建立参数的回归方程,采用线性回归方法推导出经验公式。建立了以铣削加工参数为设计变量,以铣削力、机床有效功率、零件表面粗糙度等为约束条件,以加工时间和成本为目标的优化函数。在传统遗传算法的基础上,改进了编码方式和适应度函数,对铣削参数进行优选。试验表明,该方法具有较好的实用性和有效性。

铣削;参数优化;遗传算法

0 引言

铣削参数的选取直接关系着工件的加工效率和成本,影响着工件的加工质量,不合理的铣削参数甚至会造成工件报废、铣削加工无法进行等。传统数控加工工艺通常是工作人员根据个人经验或查阅资料来选取加工速度、进给量等铣削参数。这种方法很难给出最优的参数,尤其是加工复杂零件时难以给出合理的参数,需要多次试切,降低了加工效率,增大了加工成本。国内外众多学者对此进行了大量的研究。

切削参数优化问题通常是多约束、非线性的。传统的优化算法如梯度下降法、梯度映射法、线性规划法等在求解过程中容易陷入局部最优解,很难得到理想的铣削参数。目前,针对铣削参数优化的一系列方法得到越来越多的关注。周辉、邓奕等[1]以刀具磨损寿命及材料去除率为评价因素,运用模糊正交优化法对铣削参数进行优化。邓清伟等[2]针对表面粗糙度与尺寸精度的实验数据,采用BP神经网络建立数控加工铣削参数优化模型。时政博等[3]利用铣齿功率建模预测铣齿功率大小和在线监控机床振动稳定性进行切削参数的优化,达到保护机床、刀具和提高加工效率的目的。张青等[4]提出半可行域概念,以最短加工时间和最大材料体积切除率为目标函数,以切削力、机床功率及切削扭矩等作为约束条件,利用粒子群算法实现了铣削参数优化。汪辉等[5]以加工时间和加工成本为目标函数,以主铣削力、机床功率、表面粗糙度等为约束条件,利用遗传算法对铣削速度、铣削深度及每齿进给量进行优化。耿金萍等[6]以最大生产效率为目标函数,以切削进进给力、零件表面粗糙度等作为约束条件,对铣削进给和每齿进给量进行优化。刘金栋[7]对优化变量进行了调整,利用遗传算法实现了铣削速度、铣削深度及进给量的优化。刘晓志等[8]建立了以材料去除率为目标的单目标优化函数,通过改进遗传算法中交叉概率和变异概率达到优化铣削参数的目的。Librantz等[9]以纯利润为优化目标,采用基于遗传算法的工具箱对铣削参数进行优化。Elisa Vazquez等[10]利用经验模型和粒子群算法,对铣削速度、进给量、径向切深及轴向切深进行优化,达到改善加工精度、零件表面粗糙度、加工成本等目的。

本文采用线性回归方法,推导出铣削力和零件表面粗糙度的经验公式。并以标准遗传算法(GA)为基础,改进了编码方式和适应度函数,建立了以铣削加工参数为设计变量,以铣削力、机床有效功率、零件表面粗糙度等为非线性约束条件,以加工时间和生产成本为目标的优化函数,并通过实验对算法进行了验证。

1 铣削工艺参数优化模型的建立

1.1 优化变量

铣削加工过程中,当机床、刀具和工件的参数都确定后,铣削速度、进给量、轴向切深、径向切深的选择将直接影响着工件的生产效率、加工成本及加工质量等。例如,当铣削速度较高,而进给量较小时,会出现工件表面质量下降,产生振动等现象;当进给量一定,切削深度较大时,则切削面积增大,变形力、摩擦力和铣削力都随之增大,切削深度较小时则容易产生振动现象,一定情况下都影响着刀具寿命和加工质量等。因此,本文设置模型的决策变量为铣削速度、进给量、切削深度和切削宽度。

1.2 多目标优化函数的建立

目标函数的建立应该较准确的反映客观问题。针对铣削加工,铣削参数优化的目标函数通常包括最大生产效率和最低生产成本。

(1)最大生产效率

加工一个工件所需的时间为:

(1)

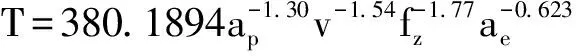
加工时间tm模型为:

(2)

式中,D为刀具铣削直径,L为铣削长度,H为待加工零件厚度,v为铣削速度,fz为每齿进给量,ap为轴向切深,Z为刀具齿数。

立铣刀使用寿命经验公式为:

(3)式中,KT、CT、q、m、x、y、u、w是常系数,ae为径向切深。

(2)最低生产成本

(4)

式中,Cl为单位劳动时间成本,Ct为每次换刀时的刀具成本。

(3)多目标优化函数

(5)式中,w1、w2为权重系数,分别反映了加工时间和加工成本对多目标优化问题的重要程度,满足w1+w2=1。tw0、CP0分别为优化前零件的加工时间和加工成本。

1.3 约束条件

(1)铣削力约束

在铣削过程中,加工所产生的各个方向上的铣削力都不能超过机床、刀具及夹具的允许值,否则会导致工艺系统的破坏。同时不易过大,否则会降低刀具寿命和工件质量等。

(6)

式中,i=x,y,z,Fi分别为x、y、z三个方向上铣削力的最大值,Fi(max)为各个方向上允许的最大铣削力,CF、b1、b2、b3、b4为常系数。

(2)机床有效功率约束

(7)

式中,F为铣削力合力,η为机床传动效率,Pmax为机床最大功率。

由于Z轴方向的铣削力较小,此处不将其记入铣削力合力中,得:

(8)

式中,Fx、Fy分别为x,y方向的铣削力。

(3)零件表面粗糙度约束

(9)

式中,Ra(max)为表面粗糙度最大允许值,CRa、d1、d2、d3、d4是常系数。

(4)铣削参数约束

(10)

1.4 铣削力和粗糙度与铣削参数的关系

在铣削实验中,所测铣削力分别为x方向分力Fx、y方向分力Fy和z方向分力Fz。由于加工中存在轴向的偏移和振动,使得Fz容易无规律的变化,且Fz远小于Fx和Fy。因此,本文主要针对Fx、Fy进行研究,实验参数及铣削力、零件表面粗糙度测量结果如表1所示。

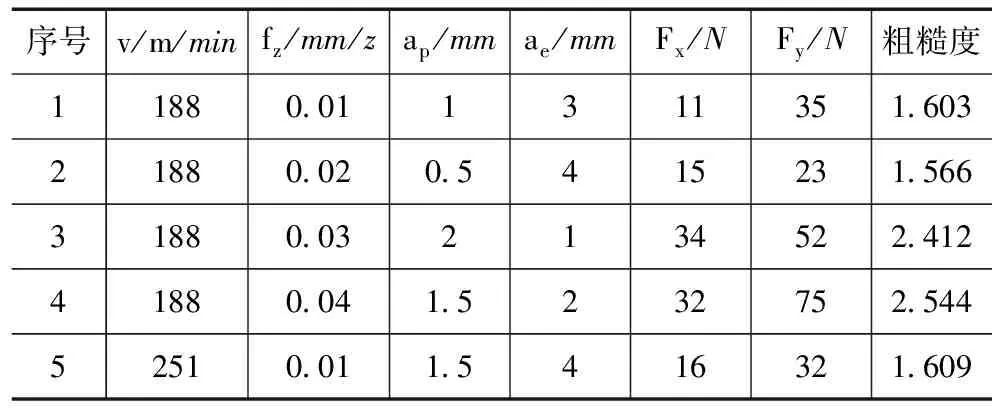
表1 铣削参数及相应的铣削力和粗糙度

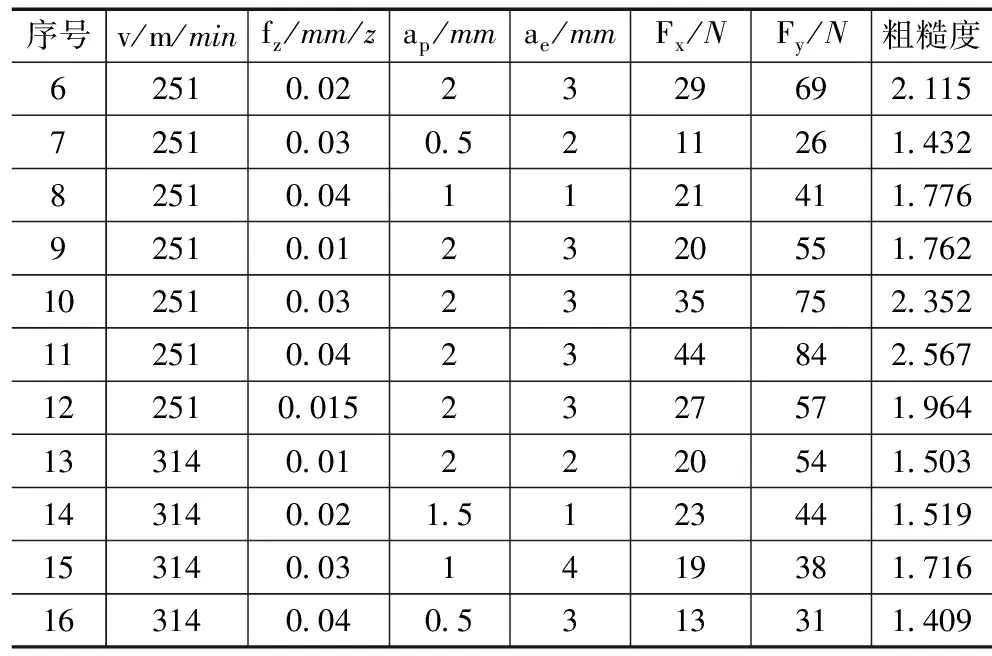
(续表)

令p=logF,c0=logCF,c1=logap,c2=logv,c3=logfz,c4=logae。则铣削力指数方程转换为线性方程,具体如下:

p=c0+c1b1+c2b2+c3b3+c4b4

(11)

式中,c0、b1、b2、b3、b4是需要求解的参数, p、c1、c2、c3、c4通过铣削力试验获得。

利用MATLAB对试验数据进行回归分析,得:

(12)

(13)

采取同样方法,得零件表面粗糙度数学模型如下:

(14)

2 遗传算法

2.1 编码方法

经典遗传算法采用二进制编码,但对较长编码串操作时容易出现误差,且计算量过大,降低了效率。针对本文参数优化中决策变量数目较多,采用格雷码编码方式。

2.2 适应度函数

适应度函数表明个体的优劣性,个体的适应度较高遗传到下一代的概率就较大;反之,遗传到下一代的概率就较小一些。由于目标函数的函数值分布上相差较大,因此本文采用均匀性适应度函数。

2.3 控制参数设置

群体规模通常取20-200。求解问题的非线性越大,群体规模就应该越大。因此本文选择群体规模为200。交叉概率始终控制着交叉算子,控制着交叉操作被使用的频度。交叉概率较大时,可使各代充分交叉,但容易使搜索随机化;交叉概率较小时,得到全局最优解的概率增大,但影响了运行速度。变异运算对交叉过程中可能丢失的遗传基因进行修复和补充,防止局部收敛。变异概率较大时,增加了群体的多样性,但可能导致搜索无效;变异概率较小时,稳定性好,但容易陷入局部最优解。本文选择交叉概率Pc=0.95,变异概率Pm=0.06。

3 优化实例

3.1 试验条件

(1) 机床、刀具及工件参数

机床型号为DMC70Vhi-dyn;刀具直径为10mm, 齿数为4,螺旋角为30°,材料为硬质合金;待加工工件尺寸为90mm×90mm×20mm,材料为钛合金。

(2) 测量装置

测力系统由Kistler9257B动态测力仪、DAQP-CHARGE-B电荷放大器、DEWE-50-USB-8数据采集系统及DEWESOFT-6-SE分析软件组成表面粗糙度测量仪采用TR100。

(3) 铣削方式

铣削方式为顺铣、干切削。

3.2 优化结果及分析

取辅助时间为10s,换刀时间为3s,单位劳动时间成本为1.5元,每次换刀时的刀具成本为2.5元。vmin与vmax分别取150m/min和320m/min,fz(min)与fz(max)分别取每齿0.01mm和0.05mm,ap(min)与ap(max)分别取0.5mm和2.5mm,ae(min)与ae(max)分别取1mm和5mm,Fx(max)与Fy(max)分别取100N与150N。

针对一组铣削参数经验值,利用MATLAB编写优化程序,实现基于标准遗传算法和改进遗传算法的参数优化,并依据铣削参数经验值和优化得到的两组铣削参数进行铣削实验,测得每组铣削参数下的加工时间、生产成本、x与y方向最大铣削力及零件表面粗糙度的试验值,优化结果与试验结果如表2所示。

表2 铣削参数优化结果及试验结果

由表2可知,用标准遗传算法和改进遗传算法对铣削参数进行优化后,加工时间分别缩短1.25%和1.85%,生产成本分别降低9.48%和11.82%,x方向铣削力分别降低4.14%和6.50%,y方向铣削力分别降低7.52%和10.70%,零件表面粗糙度分别降低8.64%和13.58%。根据此结果可判断,基于遗传算法的优化算法可达到提高生产效率、降低生产成本的目的,同时,改进遗传算法比标准遗传算法更精确,优化效果更明显。

4 结论

本文通过线性回归方法计算出铣削力和零件表面粗糙度的数学模型。以遗传算法为基础,改进了编码方式和适应度函数,建立铣削参数优化模型。以最大生产效率(即加工时间最少)和最低加工成本为目标,同时为了简化优化过程,采用权重系数变换法,转化多目标函数为单目标函数。以铣削力、零件表面粗糙度等为约束条件,达到实现铣削参数ap、v、fz、ae优选的目的。最后,通过一组实例进行分析比较,结果表明,改进遗传算法具有收敛速度快,能够迅速获得全局最优解的特性,采用优化后的参数进行铣削,能够提高生产效率、降低生产成本,为铣削过程中参数的选择提供了理论依据。

[1] 周辉,邓奕,程栋梁,等. 数控铣削参数模糊正交优化及实验研究[J]. 机床与液压,2011,39(3):66-68.

[2] 邓清伟,唐竞,王文力,等. 数控铣削参数优化的研究与开发[J]. 数字化制造,2010(22):56-58.

[3] 时政博,黄筱调,丁文政,等. 基于自适应控制技术的铣削参数优化[J]. 组合机床与自动化加工技术,2012(4):105-107.

[4] 张青,陈志同,张平,等. 基于粒子群算法的切削参数优化及其约束处理[J]. 航空精密制造技术,2010,46(1):32-36.

[5] 汪辉,刘美红,秦颖,等. 基于遗传算法的铣削参数优化研究[J]. 新技术新工艺,2010(5):41-43.

[6] 耿金萍,高顶,郭亚彬. 数控铣削参数优化的研究[J]. 制造业自动化,2011,33(10):55-56.

[7] 刘金栋. 数控铣削参数的回归分析及优化处理[J]. 装备制造技术,2011(6):1-6.

[8] 刘晓志,陶华,李茂伟. 基于改进遗传算法的钛合金TC18铣削参数优化[J]. 设计与研究,2010(5):41-43.

[9]AndreF.H.L,NivaldoL.C,ElesandroA.B,SidneiA.A,AparecidaF.C.R.GeneticAlgorithmAppliedtoInvestigateCuttingProcessParametersInfluenceonWorkpiecePriceFormation[J].MaterialsandManufacturingProcesses, 2011,26:550-557.

[10] Elisa V, Joaquim C, Ciro A.R, Thanongsak T, Tugrul O. Swarm Intrlligent Selection and Optimization of Machining System Parameters for Microchannel Fabrication in Medical Devices[J]. Materials and Manufacturing Processes, 2011, 26:403-414.

[11] 牟涛. 高速铣削钛合金Ti6AI4V的刀具磨损研究 [D]. 济南:山东大学,2009.

(编辑 赵蓉)

Optimization of Process Parameters for Milling Operations Using Genetic Algorithm

WU Ling1, ZUO Jian-min2, WANG Bao-sheng3, WANG Mu-lan3

(1.School of Mechanical engineering, Changzhou University, Changzhou Jiangsu 213016, China; 2.Jiangsu Teachers University of Technology, Changzhou Jiangsu 213001, China)

To improve productivity and reduce costs, it is very important to choose milling parameters scientifically. The regression equation of the parameters was established with the test data, and the empirical formula was deduced by means of linear regression analysis. Taking the establishment of the milling processing parameters as the design variables, optimization functions were constructed with the milling force, machine effective power and surface roughness as the nonlinear constrained conditions. The goal of the function is to get the minimum processing time and production cost. The traditional genetic algorithm was improved in the aspect of the coding method and fitness function to optimize the milling parameters. The experiment proved that the method has well practicability and effectiveness.

milling; parameter optimization; genetic algorithm

1001-2265(2014)04-0108-04

10.13462/j.cnki.mmtamt.2014.04.029

2013-01-28;

2013-03-04

江苏省自然科学基金(BK2012476);江苏省高校自然科学研究重大项目(12KJA460002);南京工程学院科研基金(ZKJ201201)

吴玲(1987—),女,江苏泰兴人,常州大学机械工程学院硕士研究生,研究方向为机电一体化,(E-mail)wuling919@163.com。

TH166;TG501

A