一种对称式直线加减速方法*

黄昭县，王志成

(1.中国科学院大学，北京 100049；2.中国科学院 沈阳计算技术研究所， 沈阳 110168;3.沈阳高精数控技术有限公司，沈阳 110168)

一种对称式直线加减速方法*

黄昭县1,2，王志成2,3

(1.中国科学院大学，北京 100049；2.中国科学院 沈阳计算技术研究所， 沈阳 110168;3.沈阳高精数控技术有限公司，沈阳 110168)

在高速高精加工中，定位时间和定位精度是衡量数控系统性能的两项重要指标。论文分析了传统直线加减速中定位时间较长的原因，在此基础上提出了采用对称思想使减速段与加速段严格对称的改进方法，并进行了仿真和实验。结果表明在保证精度的前提下，采用该方法可以缩短定位时间，能够提高定位效率。

直线加减速；高速；高精；伺服定位

0 引言

在数控加工过程中，为了使机床快速、准确地运行到给定位置，需要对电机的启停、轨迹转接等进行速度控制，对运动路径进行轨迹规划，使电机的转动平稳[1]。常见的加减速控制方法有：直线加减速、指数加减速、S形加减速、三角函数加减速等，其中直线加减速因在给定位置、速度、加速度的条件下定位时间最优而得到广泛应用[2]。

理想直线加减速控制过程可分为加速段、匀速段和减速段三个阶段。实际应用中，为了避免被控对象到达目标位置后仍有较大速度产生冲击，而使减速点提前。为了使被控对象能够到达目标位置，引入低速定位阶段。在高速运动中，低速定位阶段运行时间可能比较长，这样就造成了定位时间长的问题。文献[3-4]中采用减速段误差补偿的技术使低速定位缩短甚至消除，但它的前提是加速段向匀速段过渡时，速度刚好达到最大速度。然而实际控制中，由于加速度的不连续性，速度往往在达到最大速度的转折点处产生超调，仍然会出现低速定位阶段。为了解决这一问题，本文采用对称的思想，利用加速段轨迹规划比较理想这一特点，使减速段与加速段严格对称，以消除低速定位段，减少定位时间并保证定位精度。

1 直线加减速简介

1.1 直线加减速的原理

直线加减速控制算法标准运动过程中有三个阶段：加速段、匀速段、减速段，如图1所示，形状似梯形，所以又叫梯形加减速控制算法。第一阶段—加速段，由初始速度以恒定的加速度向最大速度递增；第二阶段—匀速段，以恒定的速度运动；第三阶段—减速段，以恒定的加速度减速到初始速度，被控对象刚好到达目标位置。

图1 标准直线加减速

1.2 直线加减速的实现思想

加减速控制的实现方法与位置伺服系统采用的何种插补算法有关，常用的插补算法有脉冲增量插补和数据采样插补[8]。本文采用的是基于数据采样插补的加减速控制，它将整个运动过程分割成时间相等的时间间隔即插补周期。插补周期不变，插补步长随着进给速度的变化而变化。速度越大，插补步长越大；速度越小，插补步长越小。

在伺服驱动器位置环控制模式下，给定目标位置、加速度和最大速度后，加减速控制算法在插补周期中断到来之前计算出当前周期的位置增量，然后加上前一个周期的位置给定得到当前周期的位置给定，底层位置环周期的刷新位置指令来驱动电机运动[3]。每个插补周期内插补步长即位置增量体现了速度的大小，插补步长越大，速度越大；插补步长越小，速度越小。

通过这种递推的方式，位置指令向目标位置递增或递减，最终到达目标位置。定位完成时，位置增量为零，速度理论上也应为零。

易知整个加减速控制实现的关键点在于位置增量即插补步长的准确计算。位置增量的计算有多种方法，经常采用的是简单直观的面积计算法[3]。在直线加减速控制算法中，加速度是恒定的，即Vk=Vk-1+Vacc；位置增量等于平均速度与插补周期之积，即ΔS= (Vk+Vk-1)/2*Δt，位置增量的计算问题转变成了速度Vk的刷新问题，已知插补周期两端的速度即可求得插补步长。

2 减速点的确定及问题分析

2.1 直线加减速中减速点的确定

直线加减速控制的三个阶段中，Vk相对Vk-1的变化规律是不同的。欲正确计算每个插补周期的位置增量，首先要判断当前运动处于哪个阶段，那么须预知各个阶段切换点的信息。伺服系统由匀速段进入减速段或由加速段直接进入减速段的位置称为减速点。减速段对伺服定位精度有重要影响，在轨迹规划插补算法中，必须要预测减速点的位置，以确定何时进入减速段。

通常确定减速点的方法有两种，一种利用进给速度、减速时间和减速时加速度等运动参数计算减速点[4]。设伺服系统的最大速度为Vmax，加速度为Vacc，减速段长度为Sd，则由直线加减速规律可计算减速区长度

(1)

v(t)=vmax-vacct

(2)

解方程(1)，(2)得

(3)

另一种方法根据在启动和停止时的加减速规律相同，利用对称性来确定减速点。设整个运动长度为S，加速段所走长度为Sc，得

Sd=S-Sc

(4)

由于实时性的要求，加减速控制算法运算时间不宜太长，故而在本文中采用后一种方法，降低直线加减速的时间复杂度。

2.2 减速点确定中存在的问题

由于采样插补控制过程实质上是将预加工轨迹按时间间隔(插补周期)离散为一系列控制点作为控制过程中的目标点[4，7]。对于这样的离散控制方式，由采样周期带来的量化误差是不可避免的。在直线加减速中，影响减速点确定的因素主要有两方面：

一方面，在匀速段中，以最大速度Vmax进给，不能保证经过整数个插补周期恰好到达理论减速点。

图2 实际减速点与理论减速点不重合

如图2所示，当被控对象运动到位置A时，当前位置加上匀速段插补步长将会超过理论减速点位置，使实际减速点滞后。这样减速段所走的位置小于加速段所走的位置，按预期减速规律将会导致被控对象定位终止时，仍有较大速度，如曲线1所示。若强行停止势必造成冲击，影响定位精度和平稳性。

为了避免这种情况，通常使实际减速点提前到位置A，如曲线2所示。这样将导致速度降为零时电机还未到达目标位置。为了使电机准确定位，必须有一个低速定位阶段，这将导致定位时间延长。

另一方面，在加速段中，速度以恒定加速度Vacc递增，不能保证经过整数个插补周期速度恰好达到最大速度Vmax。

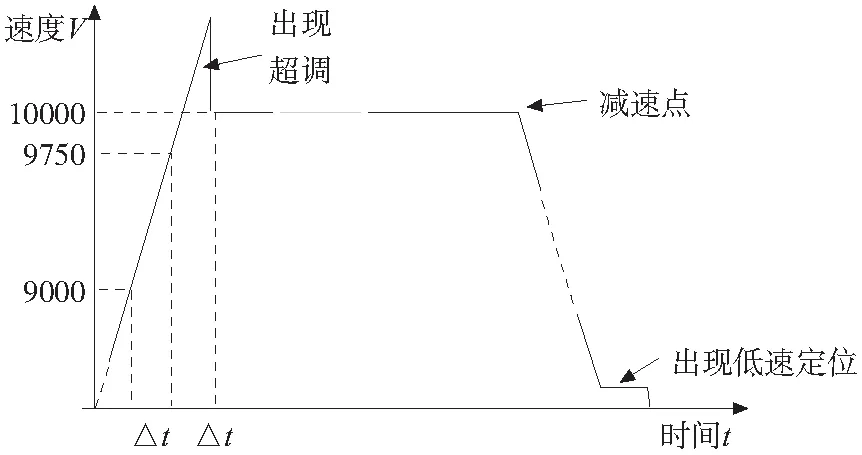
图3 加速段速度超调导致低速定位

如图3所示，加速度Vacc= 750，最大速度Vmax= 10000。当Vk= 9750时，Vk+Vacc=10500，出现速度超调。由位置增量计算公式可知，加速段最后一个插补周期的插补步长要大于理想情况下的插补步长，导致加速段位置量比理想情况下稍大。由公式(4)可知，这种情况将导致减速点位置判断提前，速度减为零时，被控对象仍然没有达到目标位置，会有一个低速定位过程。在加速度较大时，这种现象尤为明显，低速定位过程有可能比较长，使整个定位时间延长。

3 对称式直线加减速方法

由上述分析可知，减速点判断的准确与否直接影响定位精度和定位时间。为了保证定位精度，引入的低速定位段又延长了定位时间，很难使精度与时间相协调。本文采用对称的思想，使减速段与加速段严格对称，即减速段每个插补周期的插补步长与加速段一一对应，这样保证了定位终止时速度刚好为初始值的理想状态。

为了实现这种对称式的直线加减速控制方法，对传统的直线加减速做了两方面的改进：

一方面，提高判断减速点的位置的准确性。针对理论减速点与实际减速点不重合的情况(见图2)，我们增加一个预减速点，如图4所示：当到达预减速点后，如果当前位置加上匀速段插补步长超过理论减速点位置，就调整插补步长使被控对象刚好到达理论减速点。

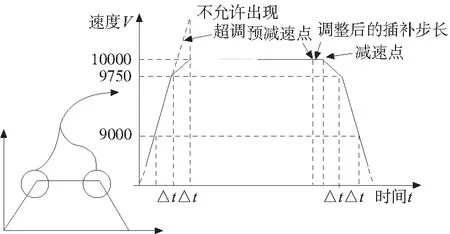
图4 减速段与加速段严格对称示意图

4 实验与结果分析

为了检验对称式直线加减速方法控制效果，使之与传统方法进行实验仿真对比。所采用的运动参数如表1，默认插补周期设定为1ms，初速度为1000 pulse/s，起始位置坐标为0。

表1 运动参数

针对匀速段中不能准确判断减速点导致定位误差，采用第一组运动参数，运行结果如图5所示。传统的直线加减速控制中，使实际减速点比理论减速点提前，在减速段后有一段较长的低速定位阶段。改进后的算法对到达预减速点后的插补步长作出调整，消除了低速定位，缩短了定位时间由原来的100个插补周期缩短为80个插补周期。

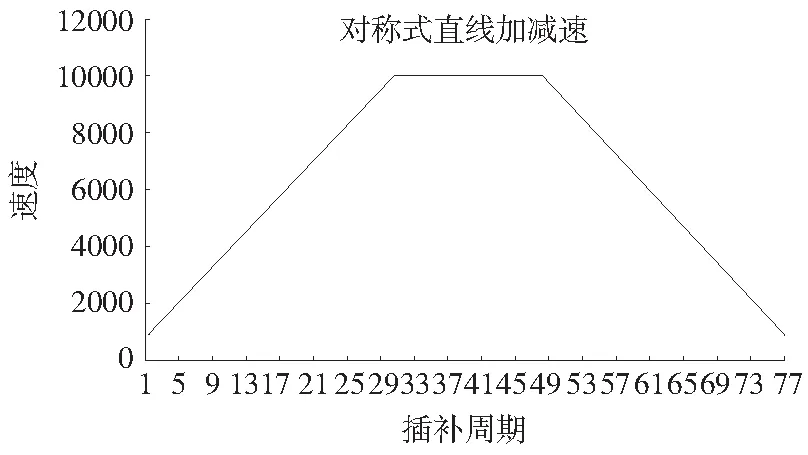
图5 减速点判断误差对比图

针对加速段中在速度向最大速度过渡时存在超调的可能，采用第二组运动参数，运行结果如图6所示。传统的直线加减速控制出现了较长的低速定位阶段，整个运动过程用了70个插补周期。采用改进后的算法，避免了速度超调，使减速段与加速段严格对称，消除了低速定位阶段，缩短了定位时间，由原来的70个插补周期缩短到了60个插补周期，提高了定位效率。

图6 加速段速度超调对比图

5 结论

(1)研究的对称式直线加减速方法消除了低速定位段，缩短了定位时间，提高了定位效率。

(2)S形加减速在理想情况下，减速段与加速段也完全对称，所以上述改进方法同样适用于S形加减速。

(3) 研究中提到的对称思想为变速变加速运动模式的加减速控制中减速点的判断提供了解决思路。

[1]黄兆斌,黄云龙,余世明.几种步进电机加减速方法的研究与应用[J].机电工程.2011,28(8):951-953,974.

[2]陈苏, 胡金高. 高性能伺服控制器算法的研究[J]. 伺服控制. 2010(8) :41-43.

[3]杨凯峰.单轴运动控制器的设计[D]. 武汉:华中科技大学，2008.

[4]郭新贵.采用线性加减速伺服系统的快速准确定位方法[J].机械工程学报.2003(7):74-79.

[5]陈友东.数控系统的直线和S形加减速离散算法[J].中国机械工程.2010(3):567-568.

[6]王晓明.电动机的DSP控制[M].北京:北京航空航天大学出版社,2009.

[7]林荣华.新型运动控制器及其核心算法设计与实现[D].广州:华南理工大学,2012.

[8]向乐萍.高速CNC变速变加速算法研究与实现[D].广州:华南理工大学,2012.

[9]于金刚.一种新型的Jerk连续加减速控制方法研究[J].组合机床与自动化加工技术.2009(8):61-64,67.

[10]卢勇.数控系统往复运动控制的研究.[D].广州:华南理工大学,2012.

(编辑 赵蓉)

A Symmetrical Linear Acceleration and Deceleration Control Method

HUANG Zhao-xian1,2,WANG Zhi-cheng2，3

(1.University of Chinese Academy of Sciences ,Beijing 100049,China; 2.Shenyang Institute of Computing Technology of Chinese Academy of Sciences, Shenyang 110168,China)

In high-speed and high-precision processing industry, the positioning time and positioning accuracy are the most important indicators in measured the performance of CNC machine tools .The reasons of positioning time longer in the traditional linear acceleration and deceleration control is analyzed.On this basis,it puts forward an improved linear acceleration and deceleration control methods whose deceleration and acceleration segments are strictly symmetrical and carries out simulation and experiment.The results show that this method can shorten the positioned time and improve the positioning efficiency under the premise of ensuring accuracy.

linear acceleration and deceleration; high-speed; high-precision; servo positioning

1001-2265(2014)04-0068-03

10.13462/j.cnki.mmtamt.2014.04.018

2013-08-10

"高档数控机床与基础制造装备"国家科技重大专项、高档数控系统在航空领域的示范应用(2013ZX04012-021)

黄昭县(1987—)，男，济南人，中国科学院大学、中科院沈阳计算技术研究所硕士研究生，研究方向为嵌入式与数控技术，(E-mail)huang9168@126.com。

TH166;TG65

A