基于K-means的最小生成树聚类算法*

欧阳浩,陈 波，黄镇谨，王 萌,王智文

(广西科技大学 计算机学院，广西 柳州 545006)

基于K-means的最小生成树聚类算法*

欧阳浩,陈 波，黄镇谨，王 萌,王智文

(广西科技大学 计算机学院，广西 柳州 545006)

传统的K-means算法只能识别出类似球形的数据集，传统的MST聚类算法虽然能识别任意形状的数据集，但对噪声和异常点十分敏感，由此提出了一种将K-means聚类与MST聚类相结合的聚类算法。此算法先使用K-means算法将数据分割成多个小的类似球形的数据集，然后对各个小的数据集的均值点采用MST聚类算法进行聚类分析。实验证明此算法具有较好的抗干扰性，并且可以识别出任意形状分布的数据集。为了评价聚类算法的性能，文中同时提出了一种新的聚类质量评价函数，实验证明此评价函数是有效的。

聚类分析;K-means;最小生成树;质量评价函数

0 引言

K-means算法[1]由于简单、快速的特点，在现实生活中得到广泛的应用[2-3]。但传统的K-means算法也存在一些缺陷[4-5]：①要求预先给定一个确定的k值；②对初始聚类中心敏感；③只能发现球形或圆形的簇；④算法对“噪声”和孤立点敏感。

MST[6-7]聚类算法是对所有的数据点建立最小生成树，再去掉最小树的若干个最大边，从而得到多个簇。此方法可以发现任意形状的簇[8]，但实际应用中容易受到“噪声”的影响[9]。

针对标准K-means算法和MST聚类算法不足，本文做了以下改进：将K-means算法与MST聚类算法结合，可以有效地减少“噪声”对聚类结果的影响，且能发现任意形状的簇。

1 K-means聚类算法和最小生成树聚类算法

1.1 K-means聚类算法

K-Means算法的核心思想是通过迭代把数据对象划分到不同的簇中，以求目标函数的最小化。其中，通常采用的目标函数形式为平均误差标准准则函数：

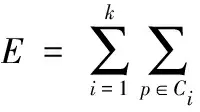
1.2 最小生成树聚类算法

最小生成树聚类算法建立在完全图的邻接矩阵基础上。首先需构建赋权完全图。在得到各点的距离的邻接矩阵后，便利用Kruskal或者Prim算法找最小生成树，再删除掉最小生成树中权值最大的K-1条边。这样将得到K个子树，这K个子树就是K个簇，如图1所示。

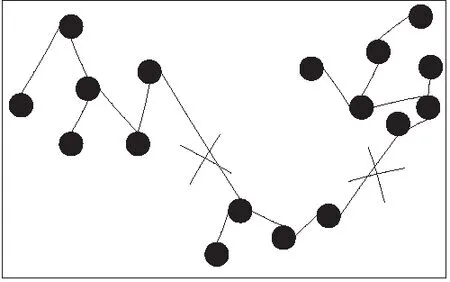
图1 MST聚类

2 基于K-means的最小生成树聚类算法

(KmMST算法)

2.1 基本思想

在传统的K-means算法中，先给定K的值，然后采用迭代的方式来完成聚类。K值一般情况下数值取得比较小，这样带了的问题是，使得聚类结果很容易受到噪声的干扰，而且只有当每个簇的大小近似，形状类似于球形时才能得到一个好的聚类结果。如果在聚类分析时，能将K取值比较大的时候，这样可以将数据对象分组成多个小的球形的簇。如图2。然后以这些小的簇的均值点建立最小生成树，删除掉C-1条最大的边，从而得到最终的分组。这样可以降低噪声或异常点对于聚类分析的影响。并且可以识别出任意形状分布的数据对象。

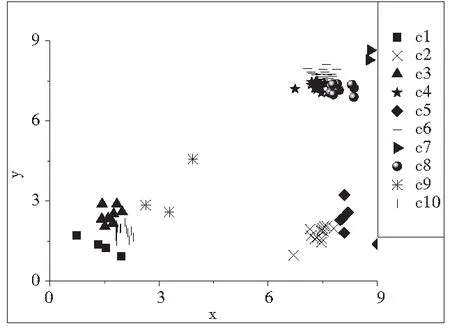
图2 KmMST中间结果(K=10)

2.2 K-means算法中K的获取

2.3 算法描述

KmMST算法描述如下：

输入：n个数据对象，调节系数r，C

输出：若干个簇

方法:

(1)计算K的值，K=|nr|(r∈[0,1])，r的常用系数为0.5;

(2)使用K-means聚类算法，得到K个子类;

(3)计算各个子类均值点之间的距离，对子类的距离进行递增排序;

(4)采用Kruskal算法，生成最小生成树;

(5)删除掉C-1条权值最大的边，从而生成C个连通分支，即C个类。

2.4 算法的复杂度分析

假定有n个数据对象，调节系数为r，算法第一步用K-means聚类的时间复杂度为O(Knt)=O(nrnt)=O(nr+1t)，其中r∈[0,1]，t为迭代次数。算法第二步生成最小生成树的时间复杂度为：O((nr(nr-1)/2)log(nr(nr-1)/2))。所以总的算法的时间复杂度为O(nr+1t+(nr(nr-1)/2)log(nr(nr-1)/2))。算法的空间复杂度为O(n+nr(nr-1)/2)。

3 一种新的聚类质量评价函数

在实际的聚类分析算法中，对于聚类结果的评价常用的评价函数是本文1.1节中的平均误差标准准则函数，此函数对于分布均匀，大小相近的数据集可以进行很好的评价，但对于任意动态变化或未知结构的数据集的评价较差[10-11]。本文根据聚类的特点，即簇内相似度尽可能高，而簇间相似度尽可能低，提出了一种新的质量评价函数,此评价函数可以对任意结构的数据按照聚类分析的定义做出相应的评价。

定义1:簇间相异度(inter-clusterdissimilarity，INTER_CD)。簇间相异度是描述聚类中，各个簇之间的相异度之和，其定义为：

其中C为簇的数目；dmin(Ti,Tj)表示簇Ti与簇Tj之间的最短距离，即：

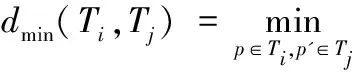
定义2:簇内相似度(intra-clustersimilarity，INTRA_CS)。簇内相似度是描述聚类中，各个簇内部数据点之间的相似度，其定义为：

其中wMST(Ti)表示簇Ti的最小生成树的权值；|Ti|表示簇Ti中数据点的个数。

定义3:簇内平均误差(intra-meandifference，INTRA_MD)。平均误差是描述数据点与它们所属簇的质心的误差的平均值，其定义为：

其中ci表示簇Ti的均值，即：

定义4：簇间平均误差(inter-meandifference，INTER_MD)。平均误差是描述数据点与其他非属簇的质心的误差的平均值，其定义为：

定义5：聚类熵(clusteringentropy，CE)。聚类熵是描述聚类中各个簇数据量的均匀分布情况，其定义为：

其中|p|为聚类中所有数据对象的个数。

定义6：聚类指数(clusteringindex，CI)。聚类指数是用于描述聚类质量的指数，其定义为：

其中α∈[0,1]。

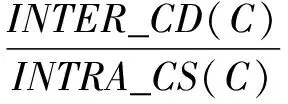
4 实验分析

实验中选择了3个不同分布特征的数据集进行计算实验，数据集通过计算机程序随机产生,数据分布见图3～图5。PC机的配置为：Intel(R)Core(Tm)2DuoCPUET500 @2.93GHz2.93GHz，2.0GB内存。软件环境是WindowXPSP3V6.2，VC6.0。

4.1 与K-means以及MST聚类算法的比较

实验1：正态分布数据集的实验。使用的数据集用D1表示，共有250个二维的数据点，如图3所示。由图3不难看出，D1明显包含2个类。图6是采用K-means聚类算法,K=2；图7是采用普通MST聚类算法，C=2。图8是采用KmMST聚类算法,其中K=|nr|=15,(n=250,r=0.5)。

实验2：大小不均匀数据集的实验。使用的数据集用D2表示，共有340个二维的数据点，如图4所示。由图4不难看出，D2明显包含2个类。图9是采用K-means聚类算法，K=2。图10是采用普通MST聚类算法。图11是采用KmMST聚类算法的分析结果，其中K=|nr|=18,(n=340,r=0.5)。

实验3：嵌套数据集的实验。使用的数据集用D3表示，共有320个二维的数据点，如图5所示。由图5不难看出，D3明显包含2个类。图12是采用K-means聚类算法，K=2。图13是采用普通MST聚类算法。图14是采用KmMST聚类算法最后的分析结果，其中K=|nr|=17,(n=320,r=0.5)

图3 实验1_原始数据 图4 实验2_原始数据

图5 实验3_原始数据 图6 实验1_K-means运算结果

图7 实验1_MST聚类运算结果 图8 实验1_KmMST运算结果

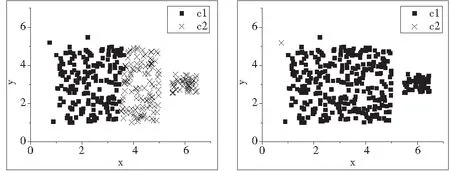
图9 实验2_K-means运算结果 图10 实验2_MST聚类运算结果

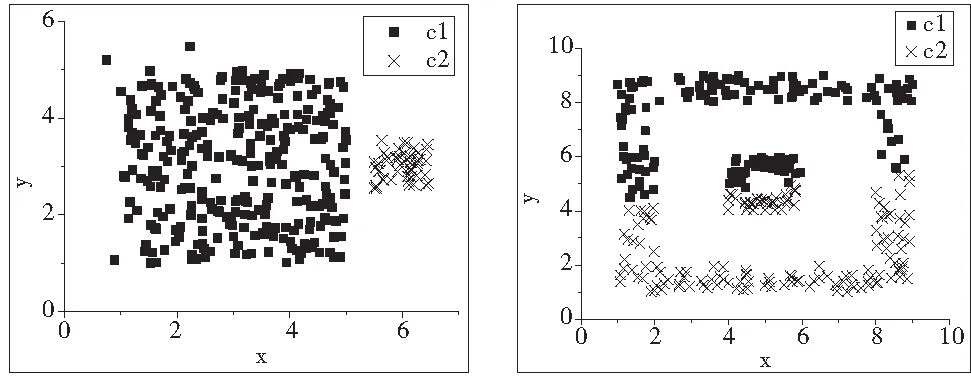
图11 实验2_KmMST运算结果 图12 实验3_K-means运算结果

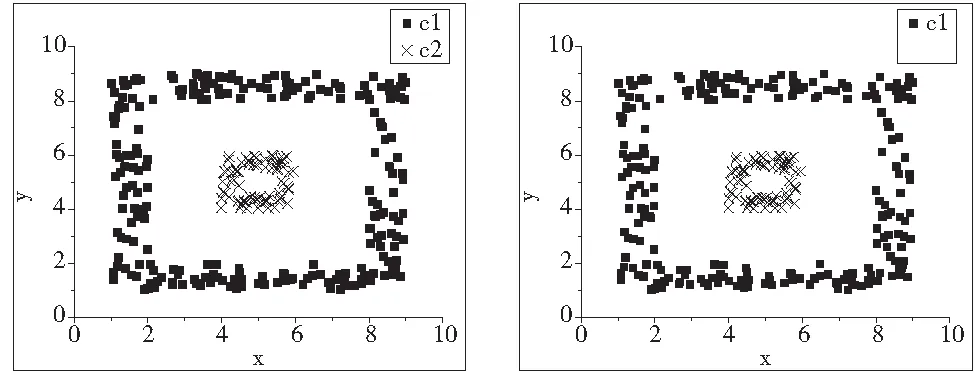
图13 实验3_MST聚类运算结果 图14 实验3_KmMST运算结

4.2 与DBSCAN算法的比较

实验4 ：DBSCAN算法中使用的人工测试数据的实验。实验中的数据集来自文献[10]当中的人工测试数据集D4、D5、D6。其中，D4有280个数据点，D5有355个数据点，D6有240个数据点。图15～图17，分别给出了使用KmMST聚类算法(r=0.5)对D4-D6的实验结果。可以看出KmMST同样能识别出这三个测试数据集。

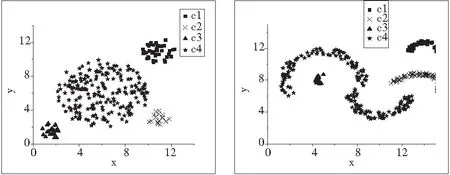
图15 KmMST对D4运算结果 图16 KmMST对D5运算结果

图17 KmMST对D6运算结果

实验5：DBSCAN算法中使用的真实数据的实验。实验采用的真实数据是SEQUOIA 2000基准数据库中的数据集，也是文献[2]中用来对DBSCAN算法进行测试的数据库。 图18给出了KmMST(r=0.5)以及DBSCAN(ε=20，MinPts=4)两个算法的性能比较结果。从图中可以看出KmMST相对DBSCAN器运行时间更少。

图18 KmMST与DBSCAN性能对比

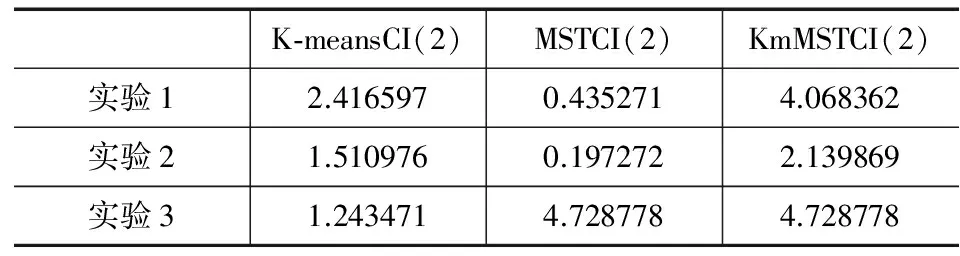
表1 聚类性能比较表

4.3 与其他改进K-means算法的比较

实验6:UCI数据集的实验。为了验证KmMST算法的有效性，本文将此算法与文献[9]中的基于密度的K-Means算法以及文献[12]中的基于遗传算法的K-Means算法进行比较，分析数据来自UCI机器学习数据库(http://ftp.ics.uci.edu/pub/machine-learning-database)，数据集为：iris，glass以及wine。表2对这几个数据集进行了描述。

表2 数据集描述

基于密度的K-Means算法中参数ε的设置在文献[13]中已验证ε=1.01时，正确率最高。基于遗传算法的K-Means算法所使用的参数设置，来自提供此算法的文献[12]：种群大小m=30，算法的最大迭代次数T=100，交叉概率pc1=0.9，pc2=0.6，变异概率pm1=0.1，pcm2=0.001，b=1000。表3给出了三种算法的性能比较。

表3 KmMST与其他改进K-Means的性能比较

5 结束语

本文提出了一种将K-means聚类与MST聚类相结合的KmMST聚类算法。此算法先将数据集分割成多个小类似球形的分组，然后对各个分组采用最小树聚类的方法来完成聚类分析。算法具有较好的抗干扰性，并且可以识别出任意形状分布的数据集，是一种有效地聚类方法。对于聚类质量性能的评价，本文提出了一个新的质量评价函数。

本文只对低维的情况进行了研究与实验，对于高维的情况仍缺少研究，而且此算法只适用于连续型的数据，不适于分组属性数据。因此对于这些问题，需要在今后的工作中作进一步的研究。

[1]MacQueenJ.Somemethodsforclassificationandanalysisofmultivariateobservations[C].Proceedingsof5thBerkeleySymposiumonMathematicalStatisticsandProbability.Berkeley:UniversityofCaliforniaPress, 1967: 281-297.

[2] 杨瑞龙,朱庆生,谢洪涛. 快速混合Web文档聚类[J]. 计算机工程与应用, 2010,46(22): 12-15.

[3] 向坚持，刘相滨，资武成，等.基于密度的K-Means算法及在客户细分中的应用研究[J]. 计算机工程与应用, 2008,44(35): 246-248.

[4]GuhaS,RastogiR,ShimK.CURE:anefficientclusteringalgorithmfordatabase.In:HaasLM,TiwaryA,eds.ProoftheACMSIGMODInternationalConferenceonManagementofData.Seattle:ACMPress, 1998: 73-84.

[5] Jiawei Han, Micheline Kamber. Data Mining:Concept and Techniques. Beijing Higher Education Press, 2001.

[6] Anil K Jain. Richard C Dubes. Algorithms for clustering data[M]. New Jersey: Prentice-Hall. Inc, 1996: 55.

[7] Charles T Zahn. Graph-theoretical methods for detecting and describing gestalt clusters[J]. IEEE Transactions on Computers, 1971, C-20(1): 68-86.

[8] 杨国慧,周春光,黄艳新，等. 最小生成树用于基因表示数据的聚类算法[J]. 计算机研究与发展, 2003, 40(10): 1431-1435.

[9] 汪闽,周成虎,裴韬，等. 一种带控制节点的最小生成树聚类方法[J]. 中国图像图形学报, 2002, 7(8): 766-770.

[10] 张惟皎,刘春煌,李芳玉.聚类质量的评价方法[J].计算机工程, 2005,31(20):10-12.

[11] 韩习武,赵铁军.一种聚类质量的评价方法及其应用[J].哈尔滨工业大学学报,2009,41(11):225-227.

[12] 赖玉霞,刘建平,杨国兴.基于遗传算法的K均值聚类分析[J].计算机工程,2008,34(20):200-202.

[13] 王莉,周献中,沈捷.一种改进的粗K均值聚类算法[J].控制与决策,2012,27(11):1711-1714,1719.

(编辑 赵蓉)

MST Clustering Algorithm Based on K-means

OUYANG Hao,CHEN Bo，HUANG Zhen-jin，WANG Meng，WANG Zhi-wen

(Computer School, Guangxi University of Science and Technology, Liuzhou Guangxi 545006, China)

Classical K-means only can distinguish similar sphere-cluster, classical MST clustering algorithm can distinguish arbitrary cluster, but it’s very sensitive to noisy and abnormal data, the paper combine K-means and MST clustering algorithm. Firstly, K-means algorithm divides data to many similar mini sphere-clusters, and then MST clustering algorithm deals with mean points of these mini sphere-clusters. Results show that the new algorithm has good anti-noisy ability, and can distinguish arbitrary cluster. In order to analyze the quality of clustering, the paper provides a new quality evaluation function. Results show the function is effective.

clustering analysis; K-means; MST; quality evaluation function

1001-2265(2014)04-0041-04

10.13462/j.cnki.mmtamt.2014.04.011

2013-08-12；

2013-09-17

广西自然科学基金项目(2013GXNSFAA019336);广西自然科学基金项目(2013GXNSFBA019280);广西壮族自治区教育厅项目(201203YB124);广西科技大学科学基金(校科自1261128)

欧阳浩(1979—)，男，湖南平江人，广西科技大学讲师，硕士，研究方向为数据挖掘和人工智能等，(E-mial)ouyanghao@tom.com。

TH122;TG65

A