基于Harris-SIFT的移动机器人视觉定位*

袁 亮

(新疆大学 机械工程学院，乌鲁木齐 830047)

基于Harris-SIFT的移动机器人视觉定位*

袁 亮

(新疆大学 机械工程学院，乌鲁木齐 830047)

目标识别和深度估计是移动机器人视觉定位的两个难点问题。针对这两个问题，文章提出了Harris-SIFT特征提取算法和基于尺度空间的深度估计算法。Harris-SIFT结合了SIFT(Scale Invariant Feature Transform)算法和Harris角点检测器，去除SIFT得到的不具有显著角点特征的特征点，以提高SIFT特征点集合的整体显著性，从而改善匹配和识别效果。此外，Harris-SIFT只需要为部分SIFT特征点生成特征描述，缩短了计算时间，适合实时应用场合。基于尺度空间的深度估计算法通过计算参考图和目标图的特征尺度比，得到图像中同一目标的近似尺寸比例，再结合参考图中目标的深度信息，便可恢复出目标图中目标的深度信息。实验表明，在移动机器人自主导航过程中，基于Harris-SIFT的目标识别体系可以准确而有效地识别目标，同时尺度空间深度估计算法也能较准确地定位目标。结合Harris-SIFT和尺度空间深度估计算法可以很好地完成移动机器人视觉定位。

Harris-SIFT；尺度空间；深度估计；视觉定位

0 引言

在导航过程中，移动机器人需要精确知道自己(或障碍物)的当前位置，以完成局部实时避障或是全局规划，这就是定位问题。自主移动机器人定位系统已有广泛研究，一般应用传感器感知的信息实现可靠的定位。近年来越来越多的定位系统使用了视觉传感器，这是因为视觉图像包含了目标的丰富信息，如颜色、纹理、形状。借助计算机视觉理论，视觉系统可以准确识别目标，估计自身位姿。因此视觉定位系统对于自主移动机器人有着重要的研究意义和应用价值。但是，视觉定位的难点是：当视角、光照发生变化或存在遮挡时，如何从图像中识别目标，提取有用信息；另外实时视频图像数据量很大，要求系统有较高的实时数据处理能力。

最近几年，不变特征在目标识别和图像匹配等应用领域上取得了巨大成功。Schmid和Mohr提出一种旋转不变性特征检测器用来解决一般的图像识别问题[1]。Mikolajczyk和Schmid扩展了该思想，提出了具有尺度不变性的Harris-Laplace检测器[2-3]。它先从固定尺度空间提取Harris角点，再使用Laplace尺度函数判断角点的尺度是否为邻域极大值。Harris-Laplace特征点具有比较好的尺度、仿射不变性，且实时性比较高，已成功应用于目标识别等领域。Jensfelt使用Harris-Laplace和SIFT描述特征进行目标识别，在室内环境下的vSLAM实验中取得了比较好的结果[4]。David Lowe提出的SIFT(尺度不变特征变换)是目前比较流行且很成功的局部特征提取算法[5-6]。SIFT从尺度空间检测特征点，再利用梯度块构建特征描述。算法可以分为四部分：①尺度空间极值检测；②特征点定位；③为特征点选择主方向；④建立特征描述。研究表明[7-8]，SIFT提取的特征点位置准确，具有良好的仿射、光照不变性，实时性较高，总体性能高于其它局部特征提取算子。目前SIFT已经成功应用于目标识别、图像视频检索、全景拼接。此后一些学者对SIFT进行了改进。Ke和Sukthankar提出了PCA-SIFT[9]：对梯度图像块进行PCA变换后，将产生36维的向量作为特征描述，代替原来的SIFT描述。实验表明，PCA-SIFT在特征匹配时速度比SIFT快，但特征不如SIFT显著，且PCA计算量比较大[7]。Andrew Stein将目标背景信息加入SIFT的特征描述，以提高匹配的精度[10]。Michael使用积分图像和积分直方图实现SIFT，以提高SIFT的实时性[11]。Mikolajczyk提出的GLOH是SIFT特征描述的一种变体，具有比较好的显著性，但计算量比较大。

本文提出一种SIFT的改进算法—Haris-SIFT。它使用Harris算子计算SIFT特征点的角点特征值，保留具有显著角点特征的特征点，以提高SIFT特征点集合的整体显著性，从而提高了匹配的准确性。实验表明，Harris-SIFT的匹配分数高于SIFT和Harris-Laplace。另一方面，SIFT特征的计算复杂度比较高，且与特征点数量成正比，因此去除”不显著”的特征点后，缩短了计算时间，提高了算法的实时性。

本文还提出了一种基于尺度空间的深度估计算法。它使用特征提取算子(如SIFT、Harris-Laplace等)从尺度空间提取特征点，每个特征点都赋予一个特征尺度，反映了目标的尺寸信息。通过匹配目标图与参考图，寻找匹配特征点对，计算相应的特征尺度比例，就可以得到目标的近似尺寸比例，从而估计出深度信息。与其它深度估计算法相比，如基于多视几何的三角测量法、基于图像结构的深度估计，本算法快速方便，具有较高的准确性，且只需要单目摄像头。实验表明，Harris-SIFT和尺度空间深度估计算法在室内机器人定位与导航实验中应用得很成功，识别准确，定位可靠。

本文结构安排如下：第2部分介绍Harris-SIFT和基于尺度空间距离的估计算法；第3部分分析基于运动和结构的三维重建方法在机器人定位中的应用；第4部分介绍机器人定位与导航系统框架；并给出实验结果和分析。最后，第5部分对本文提出的算法作出整体的评价和展望。

1 Harris-SIFT和尺度空间

1.1 Harris-SIFT

SIFT算法可以从图像中有效地提取很多尺度不变特征点。对于一幅320×240的图像，大约可以提取出400～1000个特征点。当图像存在部分遮挡时，这些局部特征点可以有效识别目标。但特征点越多，计算量越大，不适合实时应用。另外，图像发生较大的仿射形变时，匹配方法找到的特征点只是众多SIFT特征点中的一小部分，或者说很大一部分SIFT特征点在实际匹配过程中不起作用，这是因为这些特征点不具备足够的显著性。它们一方面增加了生成特征点的计算量，另一方面也增加了特征点数据库的容量和匹配复杂度，制约了算法的实时性。

上述问题与SIFT的寻找特征点的方法相关。SIFT从DoG中寻找特征点。Mikolajczyk的实验表明，DoG生成的特征尺度不如Laplacian准确[2]。另一方面，DoG抑制了边缘，适合提取blob结构，但边缘和角点也具有丰富的信息，可以加以利用。Harris-Laplace算子正是结合了Harris角点和Laplacian尺度函数，得到比较可靠的特征点。不过，SIFT特征点的位置比Harris-Laplace精确，因为SIFT特征点为尺度空间邻域内的极值点，且通过二次插值更为精确地修正了位置和特征尺寸。根据Lindeberg的尺度自动选择理论[12]:尺度空间的极值点为稳定的特征点。因此SIFT特征点定位比较准确。而Harris角点与尺度空间的极值点不一定吻合，所以Harris-Laplace特征点定位不够准确。Mikolajczyk提取一种迭代算法以改善Harris-Laplace的定位精确，但计算量会显著提高[7]。

基于上述分析，本文提出的Harris-SIFT结合了Harris角点特征和SIFT特征点的优点，其目的是为了寻找具有显著角点特征的SIFT特征点，以改善特征点集合的显著性，提高匹配效果和算法实时性。与SIFT相同，算法首先寻找DoG中的极值点作为候选特征点，然后使用尺度空间自适应Harris算子计算候选特征点邻域内各点的角点特征值(cornerness)[13]。公式如下：

(1)

cornerness=det(μ(x,σI,σD))-αtrace2(μ(x,σI,σD))

(2)

其中μ为尺度自适应的二阶矩矩阵，σI为积分尺度，σD差分尺度，Lα为梯度算子。

如果候选特征点邻域内最大角点特征值高于某个阈值，则认为该候选点具有显著角点特征，是显著的SIFT特征点，再为其生成SIFT特征描述，否则放弃该候选点。考查邻域的理由在于：SIFT从以候选点为中心的梯度块生成特征向量，充分包含了邻域信息。若邻域内存在显著的角点特征，那么这些角点信息也会被引入SIFT特征描述。另一方面，Harris角点与DoG极值点可能不重合，只计算候选特征点的角点特征值就会丢失邻域内的角点，从而丢失大量显著特征点。选择合适的邻域半径是个比较重要的问题，半径过大，特征点显著性降低，半径过小，可能会丢失显著特征点。实验结果表明，半径取2或3比较合适。

1.2 尺度空间深度估计

移动机器人视觉定位需要得到目标深度和位置信息，进而计算自身的位姿。传统的多视几何和极线几何理论估计深度算法比较复杂，且容易引入误差。本文提出的深度估计算法，在图像发生较大的仿射形变、光照变化，或存在部分遮挡时，仍能较准确地得到目标图像的深度信息，计算速度较快，且只需要单目摄像头。

该算法基于Lindeberg的尺度自动选择理论[12]。它的思想是为图像中的结构选择一个特征尺度，它由某个以尺度为自变量的函数确定，如LoG：

(3)

特征尺度与图像的分辨率无关，只与图像的结构相关，反映了结构在图像中的尺寸。因此不同图像中同一结构特征尺度的比例就近似反映了该结构图像尺寸的比例。结构尺寸比例由深度变化引起，代表了深度比例，由此可以通过特征尺度估计深度信息。

深度估计的准确性，取决于特征点提取算法和匹配算法的有效性和可靠性。可以选择Harris-SIFT(或SIFT)提取特征点，然后采用Lowe提出的匹配框架[5]：使用最近邻居距离比原则选择最佳匹配，再通过Hough变换检测几何一致性以去除误匹配。如果特征点比较多，还可以为特征点集合建立kd-tree，再搜索最近邻居，以加快匹配速度。

2 运动恢复结构和三维重建

利用多个视图间的对应关系可以恢复出场景结构以及摄像机的运动轨迹，这便是运动恢复结构的问题。通过运动和结构分析还可以进一步得到场景中各个三维点的真实坐标，即三维重建。

三维重建的算法框架如下：

①从图像中提取特征点；

②多幅图像特征匹配；

③估计基础矩阵；

④估计本征矩阵；

⑤三角测量法恢复3D坐标。

2.1 特征提取和匹配

特征提取和匹配是三维重建中的难点，一般提取角点再通过关联搜索寻找匹配点对，但是角点仍不显著，特别是不具有尺度不变性，Mikolajczyk提出的尺度自适应的角点算法可以提高角点的显著性；另外，关联搜索与窗口大小高度相关，且易受尺度变化、光照、仿射变换等因素的影响，从而产生误匹配，对后续的基础矩阵求解有很大的影响。本文使用Harris-SIFT算法提取特征点，再通过kd-tree和BBF算法快速搜索匹配点对，最后通过Hash Hough检测一致性，去除误匹配。实验结果表明，这个算法流程得到的误匹配点极少，误匹配率低于5%，从而可以显著提高基于RANSAC和MLE算法估计基础矩阵的精确性和实时性。

2.2 基础矩阵和本征矩阵

图1 极线几何：与Π中点p关联的Π′中的 点p′必定在极线l′上

基础矩阵将两幅图像的对应点联系起来，包含了摄像机在不同位置成像时的运动信息。如图1所示，p和p′通过极线l和l′关联，其中e和e′为极点，o和o′为光心，x′和x分别为p和p′的图像坐标。由此可以得极线约束方程(基础矩阵方程)：

x′TFx= 0

(4)

基础矩阵F为秩为2的3×3矩阵，可以通过匹配点对求解，一般至少需要7对匹配点。由于可能存在误匹配点对，匹配点对的坐标受噪声干扰也有误差，因此一般需要更多的匹配点对。借助鲁棒的算法，如MAPSAC(MLESAC),RANSAC等方法可以求解出比较准确的F，基础矩阵F与本征矩阵E的关系为：

F=C′-TEC-1

(5)

其中C,C′分别为摄像机内参数矩阵。若摄像机已标定，则C和C′已知，否则必须通过自标定估计C和C′，本文使用P.Sturm提出的算法进行自标定。

本征矩阵E可进一步分解为：

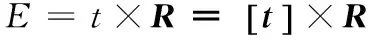
(6)

其中R为旋转矩阵，t为光心平移向量，因此通过本征矩阵可以得到摄像机的全部运动参数。

2.3 三角测量法

经过前面几步处理后，可以得到基础矩阵和本征矩阵，从而可以计算射影摄像机的成像矩阵，关系如下：

x=PXandx′=P′X

(7)

令

(8)

其中c为任意常数，b为任意向量。结合公式(4)(7)(8)便可以使用三角测量法计算点X的三维坐标。

令p1-3为P的三行，p′1-3为P′的三行，可以得到如下方程组：

xp3TX-p1X=0

yp3TX-p2X=0

xp2TX-yp1X=0

(9)

将(9)式整理成

AX=0

(10)

其中

(11)

式(10)可以通过SVD分解或数值迭代方法求解。

3 实验

本文提出的自主移动机器人视觉导航定位系统框架如图2所示。里程计为系统提供实时位姿信息，摄像头为系统提供实时图像。导航系统从目标识别和深度估计模块得到目标位置信息，进而规划机器人的运动。目标模型数据库是视觉导航系统的基础。数据库中的每个模型对应于一幅包含某个目标的图像，用Harris-SIFT特征点集合表示，同时它还包含了模型深度信息。数据库可以在系统运行之前创建，然后加载，也可以在导航过程中动态创建。基于Harris-SIFT的目标识别是整个导航系统的核心，本文采用了DavidLowe提出的识别体系[5-6]，如图3所示。首先Harris-SIFT为新得到的图像提取特征点集合，接着采用最近邻居搜索算法找到模型数据库中的匹配特征点，然后通过Hough变换检验特征点的几何一致性，去除误匹配，最后对保留下的匹配点对进行评估打分，判断是否满足识别要求，如果匹配成功，则返回数据库中的匹配模型。

3.1 实验平台与设计

图2 Frontier-II移动机器人

实验平台为Frontier-II移动机器人，如图2所示。Frontier-II使用了威盛的嵌入式主板，CPU主频1.5GHz，配有512M DDR2内存，使用Windows XP操作系统。Frontier-II采用双轮差速电机，安装了八个红外传感器，可以完成避障测距功能；外接的Logitech Quickcam USB摄像头可以以24帧/s采集320×240分辨率图像；通过Cisco的Linksys Wireless-G USB无线网卡可以很方便地与其它计算机进行通讯。实验在封闭环境中进行，过程如下：

①2.6m×4.3m的封闭室内场地中任意摆放路标和其它物品。本实验在场地四个角落和中心处各放一个路标，共5个；

②实验前手动采集路标，记录下采集时的距离信息，由Harris-SIFT提取特征点，保存为数据库。本实验中所用路标如图3所示；

图3 路标

③实验过程中，Frontier-II在场地中漫游，通过红外传感器自动避障。视觉系统通过Logitech Quickcam采集实时图像(320×240)，由目标识别模块识别目标。运动规划系统定时记录里程计数据和已识别目标的信息(估计深度和相对偏向角)；

④根据③中记录的里程计和被识别目标信息，绘制机器人运动轨迹图，描出目标位置。再与实际环境中目标的准确位置比较，分析实验结果，评价算法与导航系统的性能。

3.2 实验结果与分析

本文通过5组实验分析，验证了本文提出的算法的性能。

(1)实验1：重复率和匹配分数

图4 Graffiti图像集，视角依次为00, 200, 400, 600

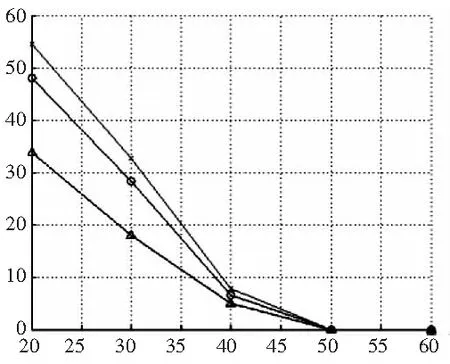
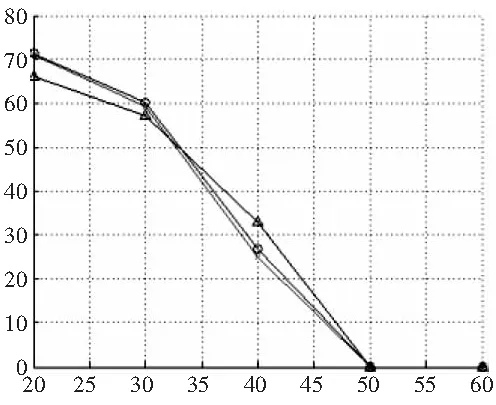
图5 Harris-Laplace、SIFT、Harris-SIFT特征点在 40% overlap error的重复率和匹配分数

实验1采用Mikolajczyk提出的评价体系[7-8]，比较了Harris-Laplace(使用SIFT特征描述)、SIFT、Harris-SIFT特征点的重复率和匹配分数。图4为实验所用测试图，拍摄视角从00每隔200变化到600。图5为Mikolajczyk评价体系得到的结果，其中SIFT和Harris-SIFT使用的是David Lowe的代码。结果表明:三种算法的重复率大致相同，SIFT的匹配分数明显高于Harris-Laplace，其中又以Harris-SIFT的分数为最高。这说明通过保留SIFT特征点集合中的显著部分，Harris-SIFT保持了SIFT定位准确的特点，同时提高了匹配分数，性能优于SIFT。图7的匹配分数图也反映Harris-Laplace特征位置不如SIFT准确，原因如前所述。

(2)实验2：算法复杂度

实验2对比了SIFT和Harris-SIFT提取和匹配特征点的时间，以反映算法复杂度差异。表1使用了Graffiti和Bark系列图像测试了Harris-SIFT和SIFT提取和匹配特征的算法复杂度。Harris-SIFT通过去掉原始SIFT得到的大部分不具有显著角点特征的特征点，缩短了生成特征描述和匹配的时间。对于Bark图像，Harris-SIFT提取特征点的时间是SIFT的一半，匹配时间仅为SIFT的1/13。

值得一提的是，Harris-SIFT对于角点比较敏感，室内环境一般比较复杂，角点比较多，Harris-SIFT可以找到足够多的匹配对以完成目标识别。因此Harris-SIFT对于室内环境下的目标识别具有较大意义，如机器人导航、地图创建和定位等。

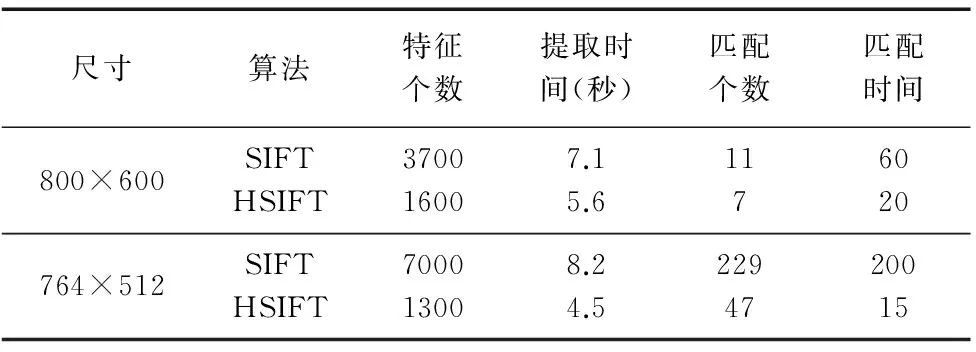
表1 SIFT、Harris-SIFT(HSIFT)提取特征和匹配的平均 时间(s)(使用的是未经优化的C++算法实现)

(3)实验3：三维重建

图6 特征匹配和极线几何

实验3给出了三维重建的部分结果。本文使用第三部分介绍的算法进行三维重建。图6所示为特征匹配后得到31对匹配点对，没有误匹配点对，再通过MLESAC算法计算F，得到的平方误差为1.11438，比较精确。

(4)实验4：深度估计

实验4利用包含同一目标的尺度变化图像组，测试了深度估计算法的性能。图7为深度估计算法的测试图。图8是通过Harris-SIFT和SIFT提取并匹配特征后得到的尺度比例。可以看到，估计结果与实际尺度基本吻合。由于SIFT特征点具有尺度、仿射、光照等不变性，在图像发生部分遮挡，或是视角发生变化时，也能可靠匹配，得到比较准确的尺度比例和深度信息。

图7 尺度随拍摄距离不同的cbook系列图。 (从左到右拍摄距离依次为100、50、75、150、200、300、400个图像单位。其中100图像单位为参考图，其余为对比测试图)

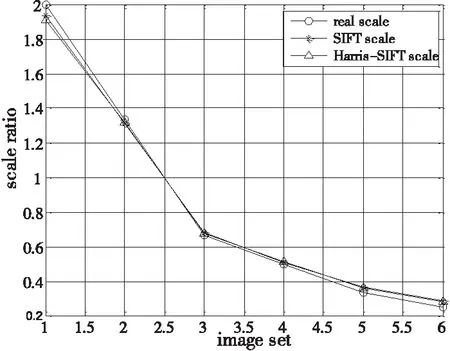
图8 实际尺度和估计尺度比例

(5)实验5：视觉导航定位

实验5在Frontier-II自主移动机器人上应用第四部分提到的导航定位系统，完成了机器人导航和定位。本文拟定以下指标来评价导航定位算法的性能：①实时性：目标识别时间；②识别率：误识别率和漏识别率；③识别能力：识别距离和角度范围；④定位精度：距离估计的可信度。

实时性：实验中目标识别模块使用的是未经优化的c++代码，在Frontier-II上运行时，识别一帧平均需3.4s，CPU占用率为100%。这主要与硬件有关，在Intel奔腾处理器上，识别一帧只需1.2s。另外，Harris-SIFT所用时间仅是SIFT的1/3～1/2。

识别率：图9描述了Frontier-II运动轨迹和目标定位情况。红色实心圆点代表识别出路标时机器人位置。在整个漫游过程中，共识别出目标43次，并且每次都识别出正确的目标，所以误识别率为0。因为每次识别时间都差不多(平均3.4s)，因此连续两次识别过程中机器人的运动距离比较接近。图中机器人的识别位置(圆点)大致等距分布，说明当目标在机器人视野中时，一般都能被正确识别出，即漏识别率比较低。

识别能力：本实验中路标相对机器人视角较小(最大不超过150)，相对距离较近(最远3m)。在这种情况下，机器人看到的路标没有发生显著的几何形变，因此识别成功率比较高。通过对目标识别模块的单独测试，我们发现：当视角发生300变化，距离路标3～5倍采集距离时，仍能准确识别目标。

定位精度：图9中同一目标的估计位置(“+”)分布得比较集中(水平和垂直方向上最大分布间距均不超过0.8m)，估计位置均分布在真实位置附近(同一目标的估计位置均落在以目标为中心、半径为0.5m的圆内，且大多数更是落在半径为0.2m的圆内)。这已经可以满足一些对精度要求不是特别高的应用场合。

需要指出的是：里程计误差会显著影响定位结果。本实验中，深度估计模块只能得到目标相对机器人的位置，需要叠加里程计信息才能得到目标在真实环境中的绝对位置。长时间运行过程中，里程计误差会逐渐累积增加，从而影响定位精度。图9中目标估计位置一般都沿逆时针方向偏离真实目标一定角度，该偏差便是由里程计的累积误差造成。实验结果表明，机器人沿场地运行两圈后，里程计角度误差达160。

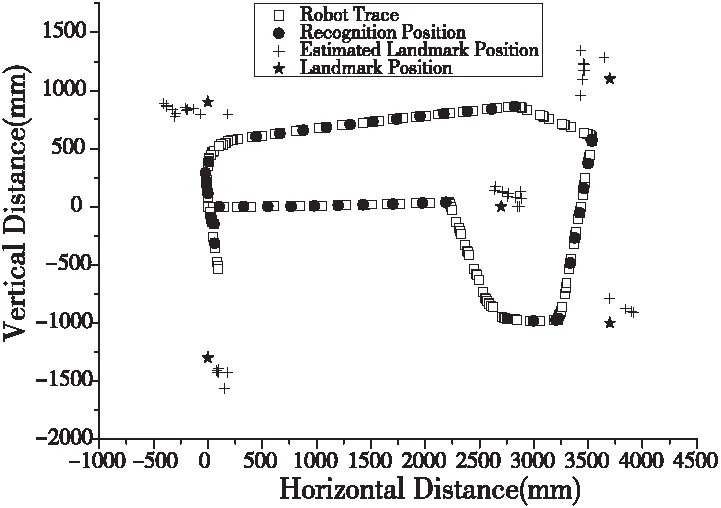
图9 Frontier-II运动轨迹及目标定位图

4 结论

本文提出的Harris-SIFT算法，结合了Harris 角点算子和SIFT的优点，提高了SIFT的匹配准确率，降低了SIFT算法复杂度，适合实时目标识别应用。本文提出的基于尺度空间的深度估计算法准确、方便、快速。移动机器人自主导航和定位实验表明，结合Harris-SIFT和尺度空间深度估计，可以准确识别目标，可靠定位。因此这两个算法对于移动机器人视觉定位具有较大的意义和较高的应用价值。

[1] Shmid.C. and R. Mohr.Local greyvalue invariants for image retrieval[J]. IEEE Trans. Pattern Anal. Mach. Intell,1997,19(5):530-534.

[2] K. Mikoljczyk and C. Schmid, Indexing based on scale-invariant features, in Proc. Int. Conf. Computer Vision, 2001:525-531.

[3] K. Mikolajczyk and C. Schmid. Scale & Affine Invariant Interest Point Detectors[J]. In International Journal on Computer Vision, 60(1):63-86, 2004.

[4] P. Jensfelt, D. Kragic, J. Folkesson and M. Bj¨orkman. A Framework for Vision Based Bearing Only 3D SLAM.ICRA,2006.

[5] D. G. Lowe. Object recognition from local scale-invariant features [C]. In Proc. of the International Conference on Computer Vision, 1999(9):1150-57.

[6] D. G. Lowe. Distinctive image features from scale-invariant keypoints [J]. International Journal on Computer Vision, 2004,60(2):91-110.

[7] K. Mikolajczyk and C. Schmid. A performance evaluation of local descriptors[J]. In IEEE Transactions on Pattern Analysis and Machine Intelligence, to appear, 2005.

[8] K. Mikolajzyk, Tinne Tuytelaars, Cordelia Schmid, et all. A comparison of affine region detectors and descriptors[J]. International journal on computer vision 2005.

[9] Ke, Y., Sukthankar, R. PCA-SIFT. A more distinctive representation for local image descriptors. In CVPR . 2004:506-513.

[10]Andrew Stein, Martial Hebert. Incorporating Background Invariance into Feature-Based Object Recognition [C]. WACV/MOTION 2005: 37-44.

[11]Michael Grabner, Helmut Grabner, Horst Bischof. Fast Approximated SIFT[C]. ACCV ,2006.

[12]Lindeberg, T. Feature detection with automatic scale selection[J]. International Journal of Computer Vision, 1998,30(2):79-116.

[13]K.Mikolajczyk, A. Zisserman, and C. Schmid. Shape recognition with edge-based features[J]. In BMVC, 2003,779-788.

(编辑 赵蓉)

Visual Localization for Mobile Robot with Harris-SIFT

YUAN Liang

(School of Mechanical Engineering, Xinjiang University, Urumqi 830047, China)

Object recognition and depth estimaiton are the two key problems in visual localization for mobile robot.To solve these prolbems, this paper presents a feature extraction algorithm called as Harris-SIFT and depth estimation algorithm using scale space. The Harris-SIFT algorithm is combined with the SIFT (Scale Invariant Feature Transform) algorithm and Harris corner dectector. It gets rid of some feature points with non-remarkable corner features in order to improve the whole significance in SIFT feature point collection and better the match and recognition performance. In addition, Harris-SIFT can be used in the real-time cases because it only take case of some of SIFT feature points and the computation time is decreased. The depth estimation algorithm based on scale space achieves the approximated dimensional scale by computing feature dimensional scale in a refernce image and objective image. Then the objective deption information in the objective images can be achieved by combining the objective depth information in the reference image. Experiments show that Harris-SIFT can accurately and quickly recognize the object in the navigation of the mobile robot. Meanwhile, the depth estimaiton algorithm in space scale also can localize the object accurately. Therefore, the visual localization for mobile robot can be improve by combining the Harris-SIFT and the depth estimaiton algorithm in the space scale.

Harris-SIFT; scale space; depth estimation; visual localization

1001-2265(2014)06-0019-06

10.13462/j.cnki.mmtamt.2014.06.006

2013-10-03；

2013-11-03

国家自然科学基金(61262059)；新疆优秀青年科技创新人才培养项目；新疆大学博士启动基金

袁亮(1972—)，男，山东郓城人，新疆大学副教授，博士，研究领域为机器人控制计算机视觉与图像处理，(E-mail)ylhap@163.com。

TH166;TG65

A