梨果实与叶片特征关联的分形研究

李凯旋，李新强，荆慧萍，沈陆明

(湖南农业大学理学院，湖南 长沙 410128)

梨的外观品质包括其大小和形状等，不同梨品种的品质不尽相同，即使同一梨品种在生长条件相同的情况下，每株产果的大小与果重差异也较明显。因此，预测挂果前梨果实的品质及整个果园的生长状态有着非常重要的意义。不少学者应用包括数学方法在内的多种方法描述果实的大小、形状等特征进行水果分级[1–3]；描述叶片的形状特征进行树种识别[4]；描述树杈结构及根系形态进行仿生设计[5–8]。笔者以湖南岳阳金秋梨为研究对象，揭示梨果实的大小、形状、果重与叶片的轮廓大小、形状特征间的分形关联，以期通过关联模型，预测果实的大小、形状与果重分布，为叶面积及形状的测量提供实际可行的方法；并整体反映同一种植园中果实与叶片的生长状态，为梨的种植及生产管理提供依据。

1 样本采集

于湖南省岳阳市云溪区兴隆科技示范园采集主栽品种金秋梨样品。采用总体抽样的方法，选择28株梨树，并从中复选出20个梨果实与20 片梨叶片为试验样本，8个梨果实与8 片叶片为检验样本。擦除样本表面灰尘，24 h 内置于背景为黑色的光箱中，采集图像机器视觉系统见文献[2]，并将果实称重。

2 图像处理

基于文献[2–3]的思想，对梨果实和叶片进行图像裁切和二值化。

2.1 图像裁切

一幅M×N 的RGB 图像可以用M×N×3 的矩阵描述，图像中的每一个像素点对应于红(R)、绿(G)、蓝(B)3个分量组成的3元组。在梨果实与叶片的RGB 图像中，目标区域为梨果实像素和叶片像素，定义裁切窗口为：

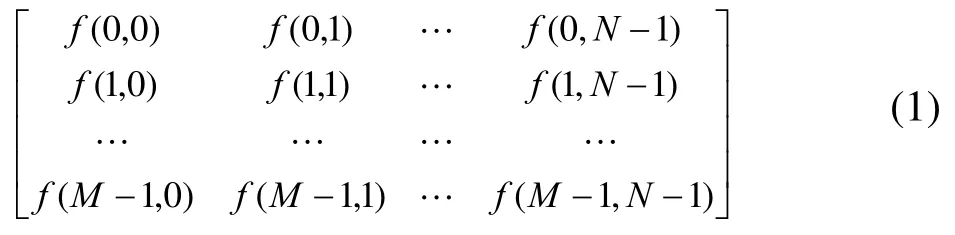
式中：点f(0,0)和f(m–1,n–1)分别由最大的果实与叶片[f(i,j)]M×N矩阵中目标区域上下及左右各增加20个像素点来确定。通过式(1)裁切果实和叶片图像去除窗口外像素，使后续的图像处理信息量少，使内存不致溢出，并提高处理速度。叶片裁切窗口为725×725×3，梨果实裁切窗口为1 024× 1 024×3。

2.2 图像二值化

作梨果实的亮度直方图(图1)和叶片的绿色G分量直方图(图2)。从图1、图2 中可看出，2个直方图均呈明显的2个区域分布，分别对应梨果实、叶片区域和背景。

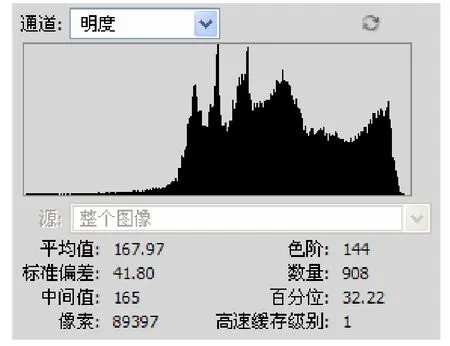
图1 梨果实的亮度L 直方图 Fig.1 L- Histogram of luminance of pear fruit

图2 梨叶片绿色G 分量直方图 Fig.2 Green G histogram of pear leaf

根据梨果实的亮度L 直方图和叶片的绿色G 分量直方图双峰分布的特点，对梨果实及叶片图像分别作如下变换：

式中：Tc和Tl分别为梨果实亮度与叶片绿色G分量阈值，通过(2)、(3)式的处理，不仅去除了果实与叶片图像背景，同时还转化成了黑白二值图像。

3 数据及处理

3.1 梨果实与叶片的周长和面积

通过细化后的二值化图像的边界像素数和区域内像素数，计算出梨果实与叶片的周长(边界像素数)和面积(区域像素数)的值(表1)。

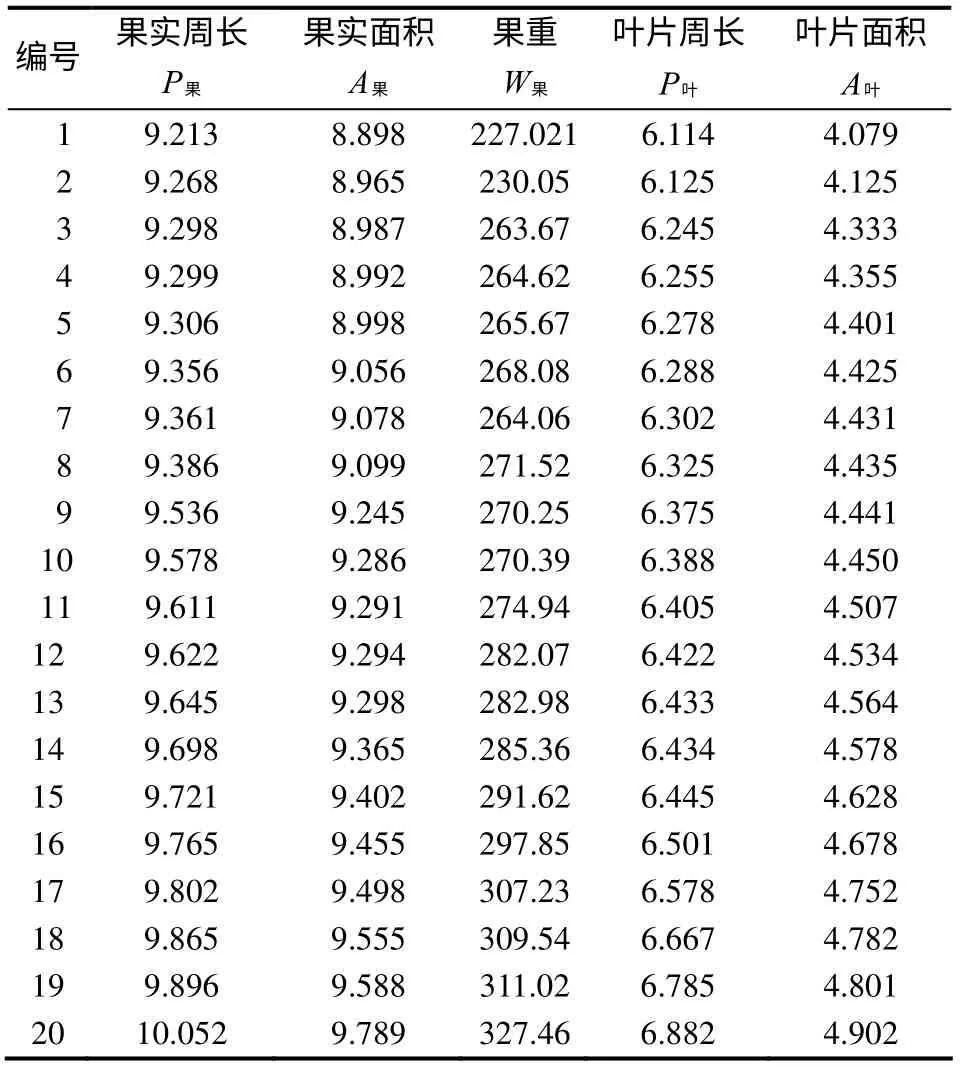
表1 梨果实与叶片的二值化周长和面积及梨果重 Table 1 Perimeters and areas of binary images of pear fruits and leaves and weight of pear fruit

3.2 分形维数的计算

根据文献[9–12]， 周长P 与面积A 之间的关系为：

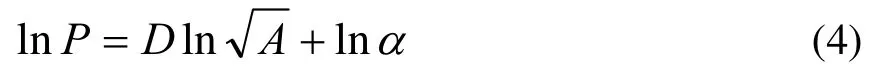
式中：α 为形状因子；D 为图形的分形维数。 对于k个图形，周长和面积分别为Pa(q=1,2,…,k)与Aa(q=1,2,…,k)，作qPln 和的线性拟合， 拟合直线的斜率为这多个图形的分形维数均值(D)，拟合直线的截距为这多个图形平均形状因子的对数( αln )。以平均形状因子为基准，由(4)式得各图 形的分形维数

他认为，学科是内涵的一部分，内涵是学科的基础。尤其是内涵建设中的质量与安全犹如1，其他建设相当于增加后面的0。如果没有1，其他做得再好也只是多加了一个0而已，毫无意义。而学科是把人、技术、有效的流程设计和管理有机整合为一体，代表医院的核心竞争力。

依据以上方法，对于经图像处理后的梨果实及叶片数字图像，以像素数计量周长与面积的梨果实

及叶片分形维数为：

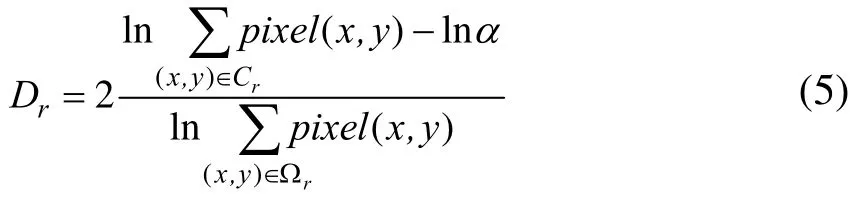
式中：rC 为梨果实及叶片边界，rΩ 为梨果实及叶片区域， αln 为点

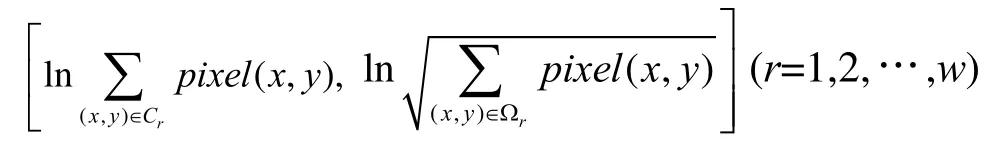
拟合直线的截距，w 为样本数。

分别作梨果实、叶片的周长–面积双对数坐标直线拟合，直线的斜率分别为梨果实、叶片的近似分形维数。根据(5)式，用各外形特征因子计算梨果实与叶片的分形维数，梨果实与叶片的分形维数的统计量列于表2。

表2 梨果实和叶片的分形维数 Table 2 Fractal dimensions of pear fruits and leaves

分别作梨果实及叶片的周长与面积的双对数坐标线性拟合，得到拟合函数：

其中x=lnP果，y=lnA果，分形维数D=1.034 2，波动范围为±0.000 6。

其中x=lnP叶，y=lnA叶，分形维数D=1.480 7，波动范围为±0.006。

3.3 梨果实与叶片的关联模型

其中x=lnP叶，y=lnP果。

分形维数D=0.795 5，波动范围±0.061，拟合精度0.910 5。

叶片面积与果实面积的双对数拟合模型为：

其中x=lnA叶，y=lnA果。

分形维数D=0.526 1，波动范围±0.081，拟合精度0.896。

叶片面积与果重的双对数拟合模型为：

其中x=lnA叶，y=lnW果。分形维数D=1.930，波动范围±0.91，拟合精度0.987 2。

4 结果与分析

植物的分形维数主要反映植物的外观形状和果皮光滑程度。梨果实形状有仿球形的特性，这与检测的果实分形维数接近于圆的分形维数1 的结果相符。但梨果实内凹的花萼和果萼无法用平面图像表示，即梨果实分形维数仅是一种近似，要精确测量其分形维数须用花萼至果萼的剖面图像。果皮光滑度是影响分形维数的另一参数，梨果实果皮光滑，叶片上有凸起的细毛，这也是梨果实的分形维数更接近于1 的原因。

8个检验样本的5个外形特征值列于表3。各模型的拟合精度值列于表4。

表3 检验样本的特征值 Table 3 The values for testing samples

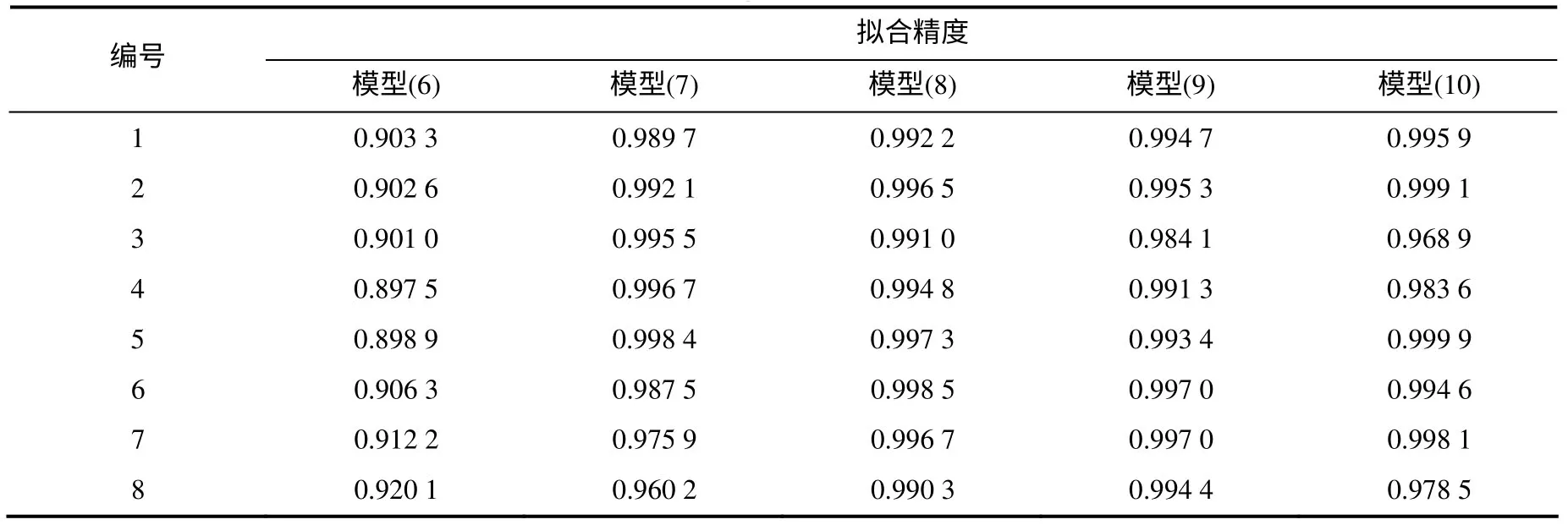
表4 各模型的拟合精度值 Table 4 Fitting precision of each models

由Origin 拟合分析可知，模型的拟合度为90%左右，说明拟合结果可信，但存在一定的误差。在检验试验中，由叶片面积和周长推测果重和果实大小与实际值相比较，精确度基本超过90%。

[1] 曹乐平．基于周长面积分形维数的柑橘品种机器识别[J]．农业工程学报，2010，26(2)：351–355．

[2] 曹乐平，温芝元，陈理渊．基于分形维数的柑橘形状与光滑度的机器视觉分级[J]．测试技术学报，2009，23(5)：407–411．

[3] 曹乐平，温芝元，沈陆明．基于色调分形维数的柑橘糖度和有效酸度检测[J]．农业机械学报，2010，41(3)：143–148．

[4] 常杰，陈刚，葛滢．植物结构的分形特征及模拟[M]．杭州：杭州大学出版社，2009．

[5] 左进波．分形理论及其在自然景物模拟中的应用[J]．科技信息，2011，25：540．

[6] 韩向峰，王婷．基于分形理论的不规则物体的造型方法研究[J]．山东师范大学学报：自然科学版，2011，26(3)：32–35．

[7] 曾兰玲，王琰．基于分形的三维梨树建模算法[J]．沈阳理工大学学报，2006，25(2)：27–29．

[8] 王安志，邵云．基于IFS 的真实感分形植物仿真与实现[J]．四川文理学院学报，2011，21(5)：87–90．

[9] Attila R Imre．Artificial fractal dimension obtained by using perimeter-area relationship on digitalized images[J]. Applied Mathematics and Computation，2006，173 (1)：443–449．

[10] Andreas Krein，Ellen Petticrew，Thomas Udelhoven．The use of fine sediment fractal dimensions and colour to determine sediment sources in a small watershed[J]. Catena，2003，53(6)：165–179．

[11] WANG Xiaoxia，ZHAO Fengqun．DAI fang，et al．Based on the fractal dimension of the entire variational image smoothing model[J]．Journal of Xi’an University of Technology，2012，28(1)：27–30．

[12] DING Baohua，LI Wenchao，WANG Fuming．Analysis of fractal image and design of fractal dimension calculation program[J]．Journal of University of Science and Technology Beijing，2009(3)：35–40．