一种最近邻像素值的极大概率滤波算法

梁立东，叶邦彦

（华南理工大学 机械与汽车工程学院，广东 广州 510640）

一种最近邻像素值的极大概率滤波算法

梁立东，叶邦彦

（华南理工大学 机械与汽车工程学院，广东 广州 510640）

图像增强是图像处理中重要的过程，其目的是消除噪声和凸显感兴趣特征。针对当前经典中值滤波算法不足，提出一种最近邻像素值的极大概率滤波算法（GPF），该算法将掩膜窗覆盖下的所有像素值视为一个像素值集，并定义评价各个元素对整个集合的影响度关系，同时提供计算这种影响度的方法，确定选值准则。最后在VC++6平台上实现该算法并与当前存在的中值滤波算法相比较。实验证明，关于最近邻像素值的极大概率滤波算法能够有效消除噪声和保留细节。

消除噪声；滤波算法；极大概率；影响度；中值滤波

图像增强是图像处理中十分重要的过程，是通过对图像优化从而达到消除噪声、凸显出图像中感兴趣的细节和特征。随着机器视觉技术的发展，图像处理技术逐渐的被应用于工业、交通、医药等行业。但在图像产生、采样、量化、编码、传输以及解码等等过程中，不可避免的会混入各种各样的噪声[1]，因此大多数情况下，在图像处理中往往需要进行图像增强，以更好的为后续处理服务。目前，常用的图像增强算法从大类上分为：1）空间域增强2）频率域增强。中值滤波算法[2-6]是空间域增强的一种典型非线性滤波算法，是将滤窗下的所有像素值由小到大排列然后选出中间的值，在保持边界及图像完整的同时能够较好消除椒盐噪声，其算法简单，针对性好。中值滤波原理的局限在于对图像增强并不十分充分，表现在：1）细的细节被当做噪声被滤掉；2）椒盐噪声密度达到一定程度后，中值滤波无法有效的完成滤波功能；3）边缘模糊。目前所采用的中值滤波算法一般是传统中值滤波算法、自适应中值滤波算法[7]以及加权中值滤波算法[8-9]。文献[7]提出了一种基于距离加权滤波算法，该算法根据滤窗下每个像素与其他像素的像素差及距离相关的权值加权总和，选出加权总和最小所对应的像素作为输出，该算法考虑不同距离的两像素间的相互影响关系，但当噪声密度大时，难以保证噪声点的加权总和一定极小而导致输出的结果仍为噪声。

正因如此，为了能够有效的消除图像中的噪声，本文提出了一种新的算法，该算法是根据掩膜窗下的所有像素值的分布规律作出的选值决策，从这些像素值中选出具有最大概率的像素值代替掩膜窗中心像素的像素值。该算法不仅对噪声具有很好的消除效果，同时对细的细节能够较好保存。

1 最近邻像素值分布分析

对于自然的原始图像，各像素点与周围的像素之间有较强的相关性，灰度值也相近。因此相对像素值本身而言，像素值分布最能表征该区域的特征。为了方便分析最近邻的像素值分布，采用一个3×3的掩膜窗去过滤图片，则被掩膜窗覆盖的九个像素点的像素值出现频数大致有以下分布情况，如图1所示。

图1 最近邻像素值分布Fig. 1 Distribution of the nearest-neighbor pixels’s gray

一般来说，带有噪声的图像，噪声点数相对整幅图像的像素数是比较少的，因而一般认为，在掩膜窗下的所有像素点，噪声点数比较少，而非噪声点则是图像本身，是连续的或者像素值出现的频数是占优的，如情况(b-d,f)，因此，在这9个像素值分布图中，总会存在多个像素值向某个像素值靠拢形成簇，而这个像素值则是这些像素值中具有最大影响。噪声点的像素值不是影响最大的，因为它们是孤立的，情况（c-f）能够说明这种情况；出现次数多的像素值也并不一定是影响最大的，因为不在像素值簇中，不能代表大多数的像素值，情况（c）正是如此。因此，为了消除噪声点，则首先需要估量掩膜窗下的每个像素值对所有像素值的影响度，选出具有最大影响度的像素值以代替掩膜窗中心的像素，达到消噪目的。

2 极大概率滤波算法的选值准则

为了计算某个像素值对掩膜窗下的所有像素值的影响度，首先作如下定义：

1）像素值集Φ，表示当前掩膜窗下的所有像素值集合，其中每一个像素的像素值均为集合中的一个元素。

2）N(xi,n)表示在像素集Φ中，与像素值xi相差为n的像素值出现的频数。其中0≤n＜256。

3）f(n)表示所讨论像素值xi对像素值集Φ中与xi相差为n的像素值xj（|xj-xi|=n）的影响系数（或概率密度），其中n＜256。随着n越大，像素值xi对像素值xi±n的影响越小，因此f(n)是一个关于n的递减函数,如图2所示 。选出合理的影响系数，对算法滤波效果十分有意义。

正态分布概率密度曲线是一个对中心附近的观测值增强而对远离中心的观测值削弱的密度函数，符合f(n)要求，因此可以采用正态分布概率密度来初始化权值f(n)，如图2所示：

由于像素值均为整数，因此f(x)的是离散的。用F表示权值序列：

图2 权值函数f(n)曲线Fig. 2 Curve of weight function f(n)

4）F(xi)表示像素值xi对像素值集Φ中的所有出现的像素值的综合影响值。集合Φ中所有像素值并不是完全相等的，每一个都与所讨论的像素值xi有偏差n，n=|xj-xi|，j=1,2…m×m。基于此，可以采用如下公式计算F(xi)：

5)最大影响值：Fmax=max{F(xi)}，则目标像素值为具有最大影响值的像素值，即：

在计算各个元素在集合中的综合影响值中，充分考虑目标元素（像素值）与集合Φ中各个元素（像素值）的关系，能够探测像素值簇位置，并且能够筛选出影响整个集合的像素值集的元素。由于噪声点在图像上是孤立存在的，因此对于掩膜窗下的像素值来说，它的影响度几乎是最小的；而对于非噪声点的像素值由于最近邻像素的灰度相近或者相同，因此它们的影响度一般都比较大，因而具有最大影响度的像素值最能代表掩膜中心的像素值。

3 算法流程

根据前述原理阐述，可以总结出极大概率滤波算法的大致流程：

步骤一：选择合适的σ，μ初始化权值序列；

步骤二：采用m×m掩膜窗扫描图像，并构造像素值集Φ；

步骤三：根据公式（3）或（4）计算各个像素值的最大影响值；

步骤四：找出最大影响值，并将所对应像素值赋给掩膜窗中心的像素。

4 实验验证

为了验证算法的可靠性与有效性，以CPU为AMD Athlon64，内存为2G的xp系统作为基础平台，采用VC++6作为编程工具实现极大概率滤波算法，并与现有的中值滤波算法做比较。

实验方法为采用采用本文所述极大概率滤波算法与中值滤波算法过滤带有不同程度噪声的目标图片。目标图片像素为300×300，掩膜窗均为3×3，权值序列为Ω={f(n)|f(n:[5,0])}。实验结果如图3所示。

其中，(I)～(V)的噪声点数分别为3 000,6 000,12 000,20 000,40 000，(a)为带椒盐噪声的源图像，(b)为采用极大概率滤波消噪后的效果图，(c)为采用传统中值滤波消噪后的效果图。

为了客观的估量消噪效果，一般采用PSNR与MSE值评价，PSNR越大，MSE越小，滤波效果越好。实验一的处理后图像与原图像的PSNR与MSE如图4所示。

图3 不同噪声程度的滤波效果比较Fig. 3 Comparision of Filtering Effect with Different Degree Noising Image

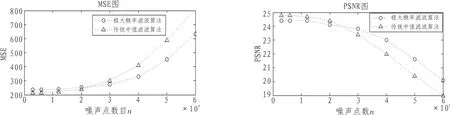
图4 两种滤波算法的MSE和PSNR图Fig. 4 Comparision of MSE and PSNR of Two Filtering Algorithm

从实验一中的图3的（I）至（V）可以看出，在噪声点数在12 000及以下时，极大概率滤波算法与中值滤波算法对椒盐噪声的过滤效果差别不大，但随着噪声点数增多，中值滤波算法的效果明显不如本文所述的极大滤波算法好，尤其在带有20 000点及以上椒盐噪声的图像，中值滤波算法过滤后的图像仍存在很多噪声点，并且噪声点存在于整幅图像；而本文所述极大概率滤波算法过滤后的图像存在少量噪声点，并且在连通域内几乎不存在残余噪声，而仅分布在连通域的边缘。极大概率滤波的这种效果十分有利于图像的后续处理。图4的MSE图与PSNR图也证明这一结果。

5 结 论

针对存在的中值滤波算法不足，提出一种关于最近邻像素值的极大概率滤波算法，该算法将掩膜窗覆盖下的所有像素值看成一个像素值集，并定义了评价各个元素对整个集合的影响度关系，同时提供了计算这种影响度的方法，确定选值准则。最后在VC++6平台上实现该算法并与当前存在的中值滤波算法相比较。实验证明，关于最近邻像素的极大概率滤波算法具有更大的PSNR值和更小的MSE值，不仅能够更有效的去除噪声，同时能够更好的保存图像中的细节。该算法对彩色图像同样适用。

[1]张旭明,徐滨士，董世运.用于图像处理的自适应中值滤波[J].计算机辅助设计与图形学学报,2005,17(2):295-299.

ZHANG Xu-ming,XU Bin-shi,DONG Shi-yun. Adaptive median filtering for image processing[J].Journal of Computer-Aided Design & Computer Graphics, 2005,17(2):295-299.

[2]倪臣敏，叶懋冬，陈孝春.一种改进的自适应中值滤波算法[J].中国图像图形学报,2006,11(5):672-678.

NI Chen-min,YE Mao-dong,CHEN Xiao-chun.An improved adaptive median filter algorithm[J].Journal of Image and Graphics,2006,11(5):672-678.

[3]张恒,雷志辉,丁晓华.一种改进的中值滤波算法[J].中国图像图形学报,2004.9(4):408-411.

ZHANG Heng,Lei Zhi-hui,DING Xiao-hua. An improved method of median filter[J].Journal of Image and Graphics,2004,9(4):408-411

[4]鲍华,樊瑜波,饶长辉,等.基于均值查找的快速中值滤波算法[J].四川大学学报,2011,43(2)76-79.

BAO Hua,FAN Yu-bo,RAO Chang-hui,et al.Fast median filtering algorithm based on mean searching[J].Journal of Sichuan University:Engineering Science Edition,2011,43(2):76-79.

[5]黄宝贵,卢振泰,马春梅.改进的自适应中值滤波算法[J].计算机应用,2011,31(7):1835-1837.

HUANG Bao-gui,LU Zhen-tai,MA Chun-mei.Improved adaptive median filtering algorithm[J].Journal of Computer Applications,2011,31(7):1835-1837.

[6]Toprak A,Guler I.Suppress of noise in medical images with the use of fuzzy adaptive median filter[J].Journal of Medical Systems,2006,30(6):465-471.

[7]金良海，李德华，姚行中.自适应距离加权的中值滤波算法[J].模式识别与人工智能,2007,20(4):577-581.

JIN Liang-hai,LI De-hua,YAO Ming-zhong. Adaptive distance-weighted median filtering algorithm [J].Pattern Recognition and Artificial Int elligence,2007,20(4):577-581.

[8]李迅波,蒋东升,王振林.梯度相似性的椒盐图像加权中值滤波算法[J].电子科技大学学报,2012,41(1):114-119.

LI Xun-bo,JIANG Dong-sheng,WANG Zhen-lin.Weighted median filtering of im based on grads similarity[J].Journal of University of Electronic Science and Technology of China,2012,41(1):114-119.

[9]邓秀勤,熊勇.用于图像处理的加权中值滤波算法[J].计算机技术与发展,2009,19(3):46-51.

DENG Xiu-qin,XIONG Yong.Weighted median filtering algorithm for image processing[J].Computer Technology and Development,2009,19(3):46-51

A great probability fi lter algorithm based nearest-neighbor pixels’ gray

LIANG Li-dong, YE Bang-yan
（School of Mechanical & Automotive Engineering,South China University of Technology,Guangzhou510640,China）

Image enhancing is an important process when image processing ,which aims at denoising and highlighting interesting parts in an image.Directing at the disadvantage of traditional median filter ,presents the Great Probability Filter Algorithm (GPF) based nearest-neighbor pixels’ gray value.The Algorithm treats the pixels’ value as a value set,and defines a Influence Degree between an element and the set,and determine the GPF Criterion.And finally realize the GPF algorithm in VC++6 and compare it with traditional median filter algorithm.Experiments show that the GPF algorithm can denoise image effectively and attain detail in image.

image denosing; filtering algorithm; great probability; influence degree; median filter

TN919.8

A

1674-6236(2014)07-0181-03

2014-01-18稿件编号201401137

国家自然科学基金资助项目(50875089)

梁立东(1988—)，男，广西来宾人，硕士。研究方向：机器视觉与智能控制。