高速车削TC11分形特征实验研究*

郑光明 赵 军 程 祥 赵国勇

(①山东理工大学机械工程学院，山东 淄博255049;②山东大学机械工程学院，山东 济南250061)

钛合金由于具有良好的力学性能、比强度高、高温及低温性能优良、抗腐蚀性能优异等突出特点，在航空航天、船舶、石油化工、汽车、生物医学等领域中广泛使用。随着钛合金应用的日益广泛，如何获得高的加工表面质量、提高刀具的使用寿命等成为丞待解决的问题。

高速切削加工过程是一个复杂、非线性的变化过程，而分形理论是非线性科学研究中十分活跃的一个分支，为解决复杂的非线性问题提供了一种行之有效的方法。分形理论对描述具有标度规律特征的自然现象有很好的适用性，因此分形理论的引入，为有效地分析切削力动态特性、刀具磨损、加工表面形貌等的复杂性带来了希望。

Mandelbrot教授在1975年第一次引入了分形的概念，经过30多年的发展，分形几何作为处理自然界复杂现象的数学工具，在摩擦学、刀具磨损、表面形貌等机械工程领域得到广泛的应用［1-4］:应用盒计数法对微细铣削加工表面形貌进行研究［5］，结果表明，微细铣削加工表面具有明显的分形特征;运用分形理论对磨合过程中表面形貌的变化规律进行表征研究［6］，建立了磨削参数与磨削表面分形参数之间关系的理论模型［7］，建立了分形参数和磨合过程的磨损深度之间的数学模型［8］;针对涂层刀具高速铣削高硬钢，用一个广义的公式建立了表面粗糙度和刀具磨损的分形维数之间的关系［9］。

本文针对难加工材料TC11，通过高速切削实验，对刀具寿命、切削力及加工表面粗糙度等进行研究，并借助分形几何理论，计算切削力的分形维数，研究高速切削过程的分形特征。

1 实验

工件:实验用的工件材料为TC11，是一种α+β双相钛合金材料，其名义成分为Ti-6.5Al-3.5Mo-1.5Zr-0.3Si。TC11材料的物理机械性能如表1所示，TC11具有良好的综合机械性能、高温强度、密度小、非磁性、热膨胀系数小、热导率低、容易烧结及对环境无污染等特点，弹性模量约是不锈钢及铝材的一半。它是目前我国航空发动机使用量最大、使用温度较高的钛合金之一，广泛用于制造转子、叶片、盘件等构件。

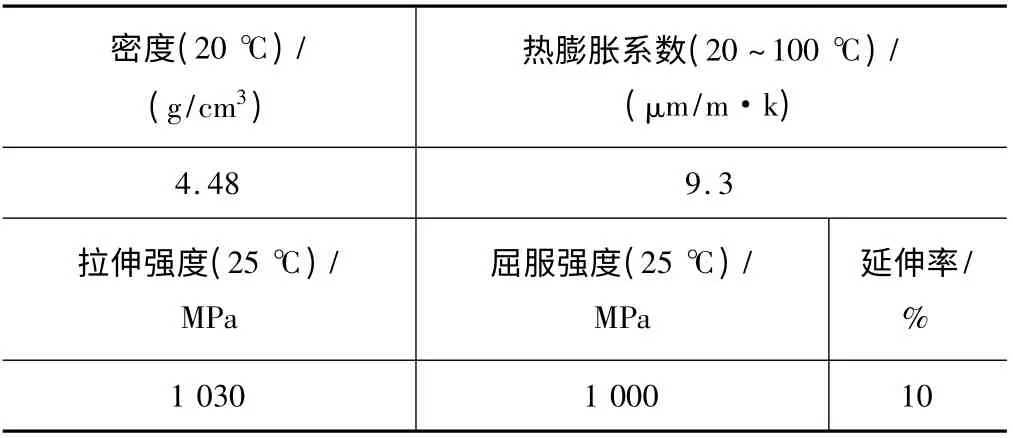
表1 TC11材料的物理机械性能［10－12］

刀具:采用美国Kennametal公司的非涂层硬质合金刀具K313和PVD涂层硬质合金刀具KC5510(型号为SNGG120408FS)。其中，KC5510材质结构为晶粒细化的硬质合金，配以先进的TiAlN涂层。选用PSSNR2020K12型号的刀杆。刀具几何角度为:前角γ0=4°，后角α0=8°，主偏角Kr=45°，刃倾角λs=0°。切削参数为:v=80-100 m/min，f=0.14-0.2 mm/r，ap=0.35-0.5 mm。

测试仪器及检测方法:采用重庆迪加科技公司的DC CSM19型车削测力仪对3个方向的测力仪进行采集，切削力测量装置连接示意图如图1所示，包括压电式测力仪，DJ-CL-1型三向力电荷高精度线性放大器和数据采集系统。对工件加工表面粗糙度的测量采用的是TR200型便携式表面粗糙度仪。每切削一段长度，除了采集切削力和测量加工表面粗糙度之外，还要利用万能工具显微镜观察刀片前后刀面的磨损情况。此实验在CA6140普通车床上进行，切削条件为干切削。

2 结果与分析

刀具后刀面磨损量随切削时间的变化曲线如图2所示，从图中可以看出，涂层刀具KC5510的抗磨损能力明显优于非涂层刀具K313。虽然在v=100 m/min切削时，刀具磨损速度明显加速，KC5510的磨损曲线仍然可以区分出刀具磨损的3个阶段:磨损初期、稳定磨损期和急剧磨损期。

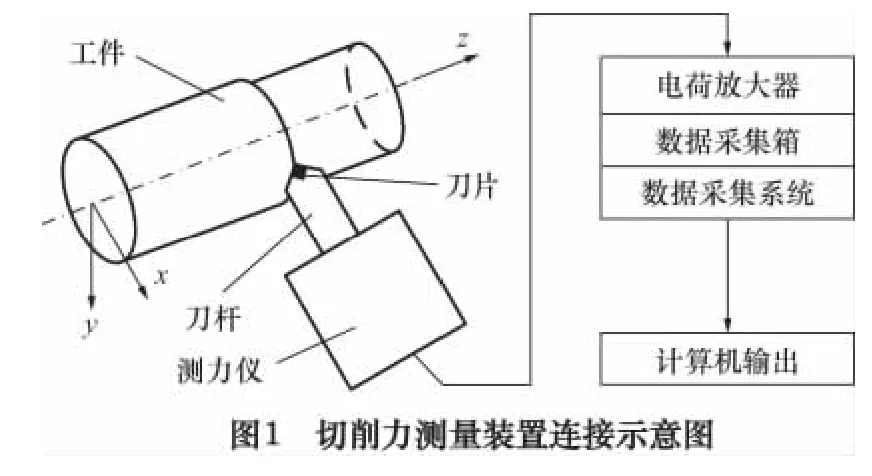
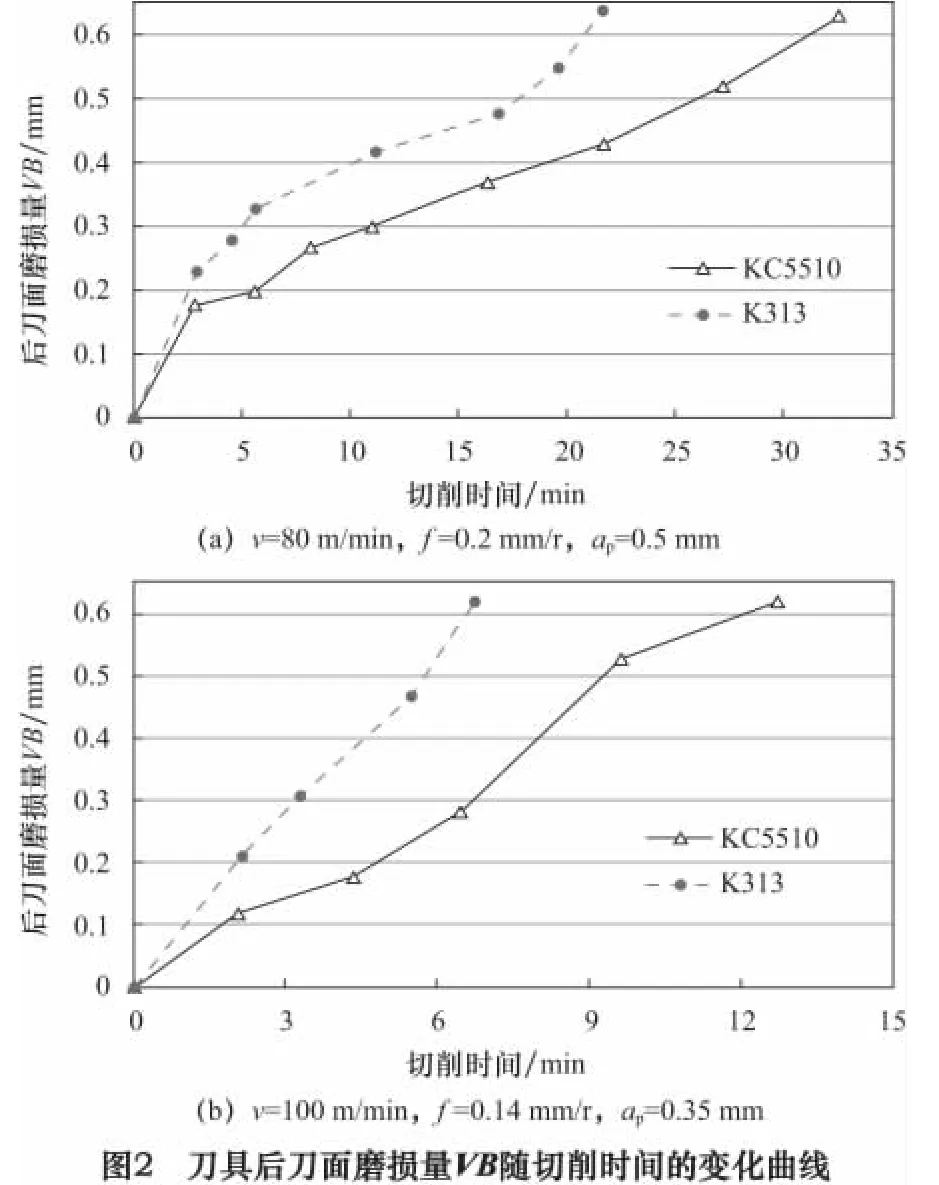
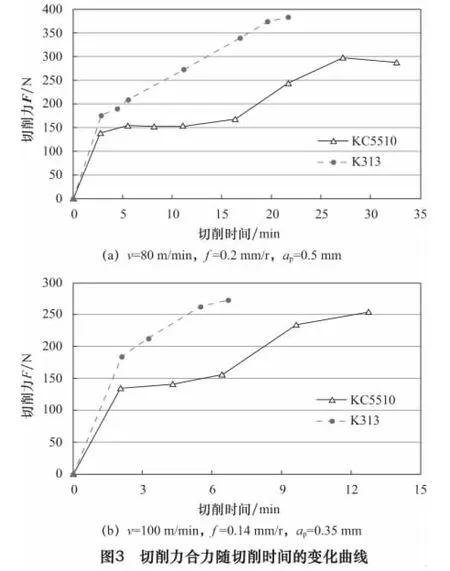
图3所示为切削力随切削时间的变化曲线，与图2对比可见，切削力的变化趋势与刀具磨损曲线的变化趋势相似。切削初期，新刀刃与工件间接触时存在一个磨合期，刀具后刀面会迅速磨损，切削力迅速增大;在稳定磨损期，切削过程相对稳定，刀具后刀面磨损变慢，切削力也相对平稳，增加缓慢;在急剧磨损期，由于切削过程中积聚的热力的综合作用，刀具后刀面随着切削的进行磨损急剧增加，切削力也迅速增大。

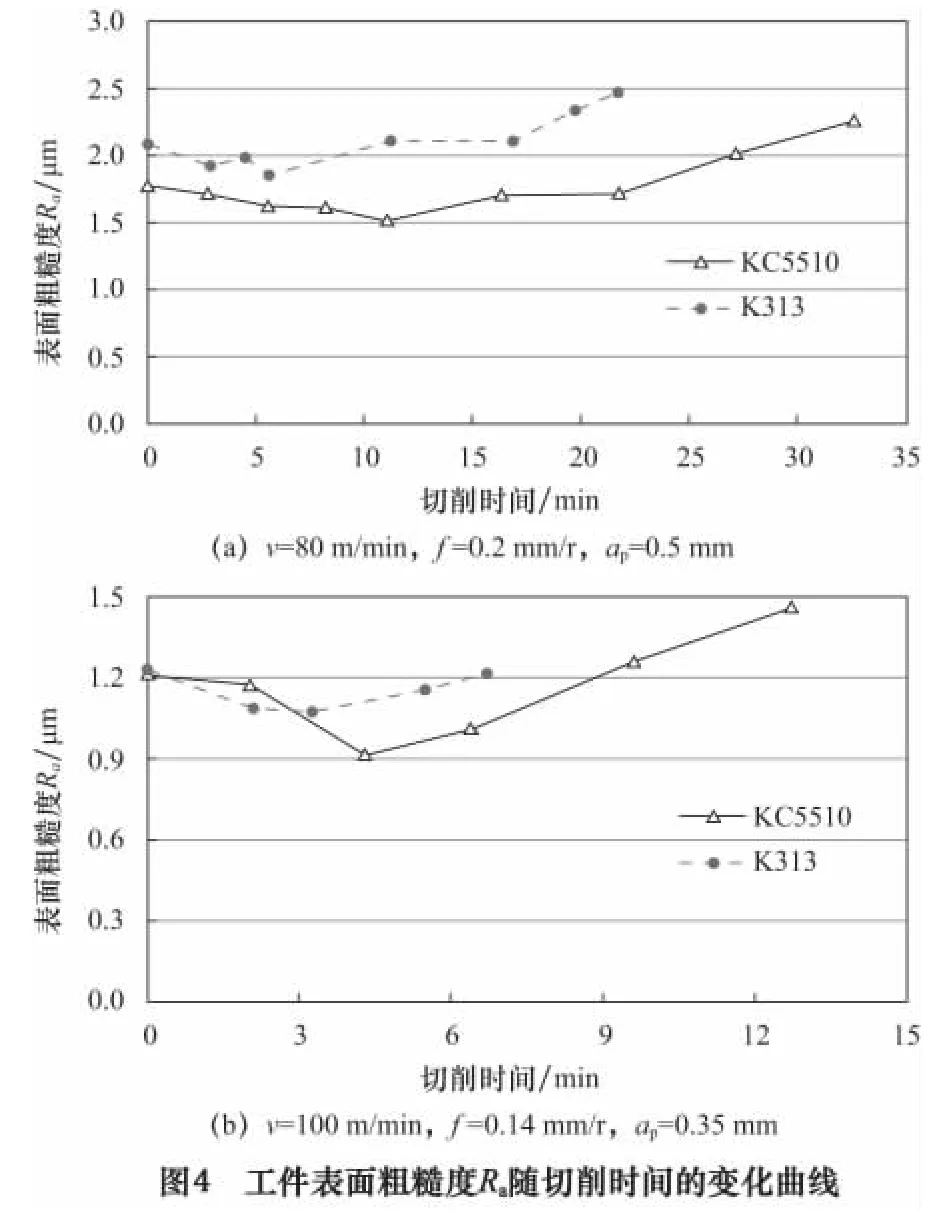
图4所示为工件加工表面粗糙度Ra随切削时间的变化曲线，从图中可以看出，表面粗糙度Ra值在刀具初期磨损期和急剧磨损期较大，在中间的稳定磨损期相对较小。这主要是因为，新切削刃上难免存在一些微小的缺陷(如微裂纹、微毛刺、微凸体等)，在切削初期，切削刃与工件接触，逐渐磨去切削刃上存在的这些微缺陷，致使此切削过程不稳定，导致切削初期加工表面粗糙度Ra值较大;随着切削的进行，刀具进入稳定磨损区，切削力也相对稳定，切削状态平稳，表面粗糙度Ra值较小，表面加工质量相对较好;但当进入急剧磨损期后，刀具磨损加剧，切削力迅速增大，容易引起机床振动，切削过程不稳定，使得表面粗糙度值增大，加工质量变差。

分形维数是描述分形特征的重要参数，其值的大小可以表征切削状态的平稳性和切削系统的复杂程度。本文选择了计算关联维数的Higuchi方法［13］，这种方法在计算离散数据时有很高的灵敏度。其计算的基本思路是［14-16］:从实验中按时间测得n个离散的数据点xi(i=1，2，…，n)，这些离散的数据点称为时间序列，根据时间序列组建k个m维的向量yk(m＜n)，使得y1=(x1，x2，…，xm)T，y2=(x2，x3，…，xm+1)T，…，yk=(xk，xk+1，…，xn)T。研究任意两个m维的向量yi与yj的关联程度，得到关联维数的表达式:

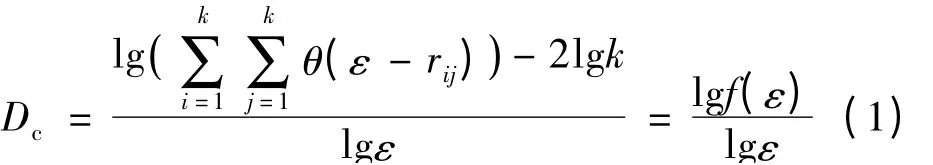
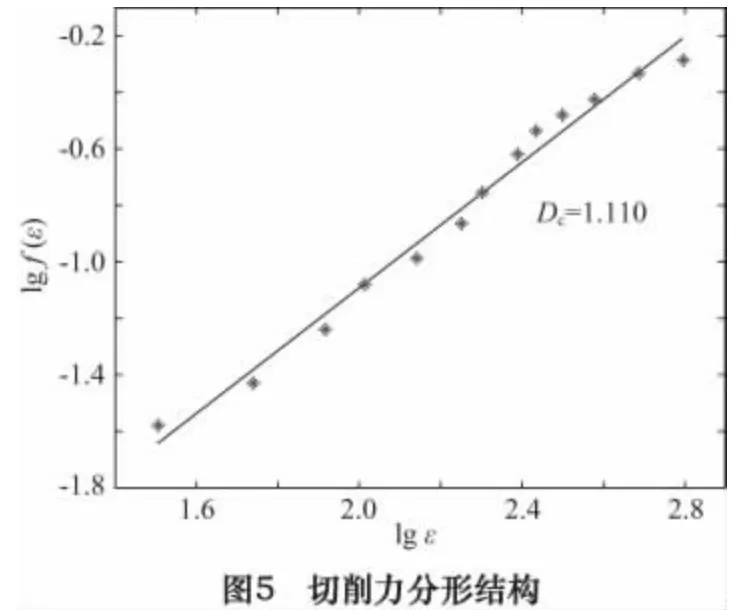
式(1)中:ε是一个小的正数，rij=|yi-yj|，θ(ε-rij)=1(当ε-rij＞0)或θ(ε-rij)=0(当ε-rij≤0)。如果rij＜ε，则yi与yj具有很强的相关性。这样选取不同的ε值，做出lg f(ε)与lgε的关系曲线，ε在一定范围内，曲线出现直线段部分，应用最小二乘法拟合这部分数据点对，所求得的拟合直线的斜率即为分形维数值Dc(如图5所示)。

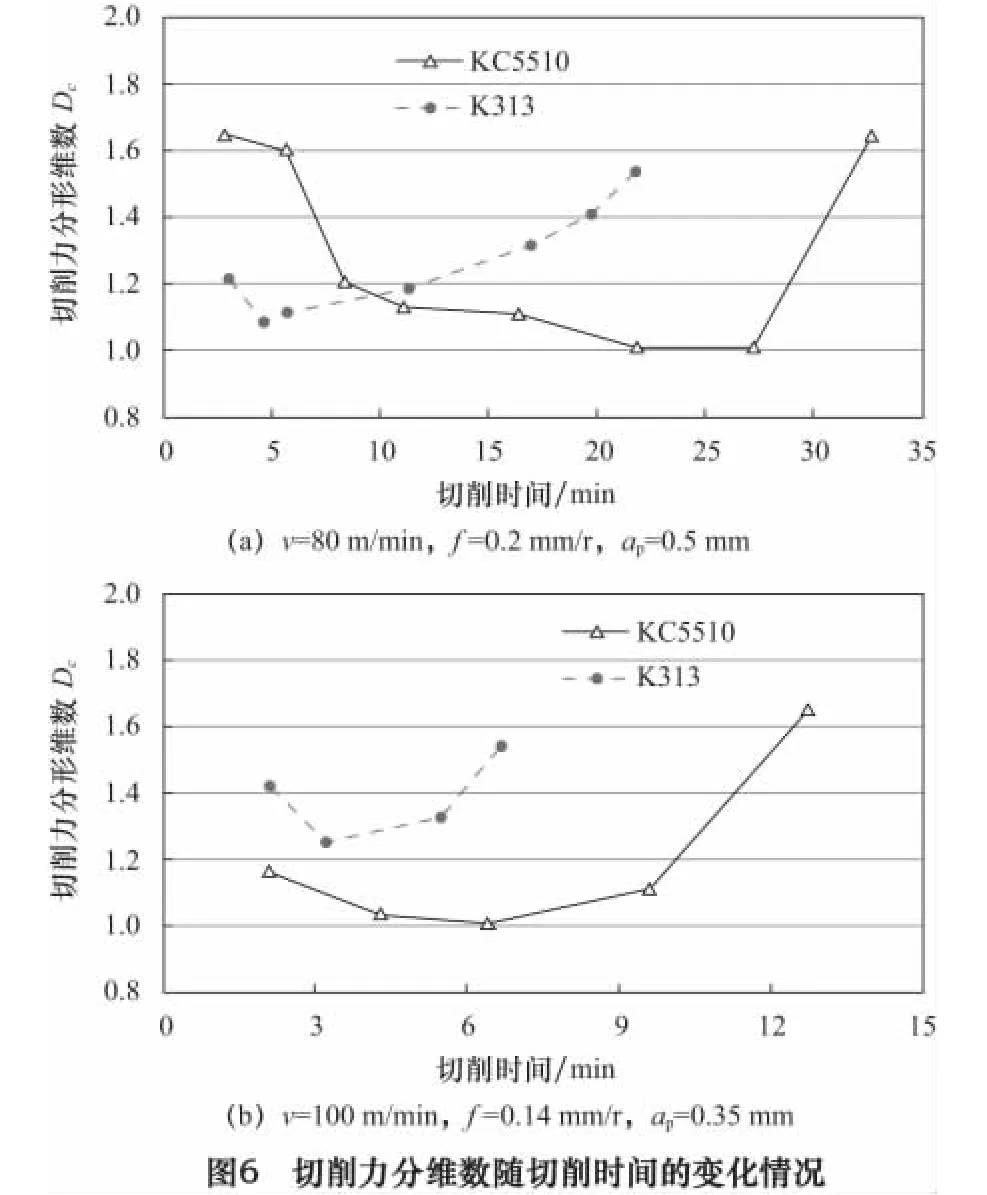
根据关联维数的计算方法，计算了切削过程中各阶段切削力的分形维数，图6所示为两种刀具切削TC11时切削力分形维数随切削时间的变化曲线。由图6可以看出，切削力分形维数随着切削的进行，呈现先减小后增大趋势。在切削初期和末期，分形维数值相对较大，而此切削阶段切削状态不稳定，表面粗糙度Ra的值较大。切削力分形维数值在稳定磨损期较小，说明在此阶段切削系统稳定，切削状态平稳，所以分形维数的变化趋势与表面粗糙度Ra的变化趋势相类似(图4)。对比刀具磨损曲线(图2)可见，分形维数随切削过程的变化规律与刀具磨损的3个阶段存在一定的对应关系:在磨损初期和急剧磨损期刀具的磨损速率较高，刀具在稳定磨损期磨损速率较小，而切削力分形维数值正是在稳定切削时较小。

根据切削力分形维数在刀具磨损3个阶段的变化特点，在切削过程中，可以通过在线观察分形维数值的变化，来判断刀具的磨损情况、加工表面粗糙度情况:分形维数值开始变小，说明切削状态平稳，加工表面粗糙度值小，刀具磨损速率也相对缓慢，此时刀刃可以用来继续切削;分形维数值变大时，说明此时的切削系统复杂，切削过程不稳定，加工出的工件表面粗糙度值变大，刀具磨损加剧，刀具接近失效，为保证加工质量，此时可以考虑停车更换新刀刃(或新刀片)。

3 结语

本文通过高速干切削航空航天领域常用的钛合金TC11实验，借鉴计算关联维数的方法，研究了切削力分形维数，研究了加工表面粗糙度、切削力及分形维数在刀具磨损的不同阶段的变化规律，得到以下结论:涂层刀具KC5510的抗磨损能力明显优于非涂层刀具K313;切削力的变化趋势与刀具磨损曲线的变化趋势相似，切削力分形维数的变化趋势与表面粗糙度Ra的变化趋势相同。切削力分形维数的大小可以反映切削过程的平稳性，当分形维数值较小时，加工表面粗糙度值小，刀具磨损速率缓慢，而当分形维数值较大时，加工表面粗糙度值大，刀具磨损迅速。通过本文的研究，可望在预测工件加工表面质量和刀具磨损状态等方面发挥积极的作用。

［1］葛世荣，朱华.摩擦学的分形［M］.北京:机械工业出版社，2005.

［2］朱华，姬翠翠.分形理论及其应用［M］.北京:科学出版社，2011.

［3］赵旭艳.刀具磨损的分形表征［D］.大连:大连轻工业学院，2007.

［4］葛世荣，索双富.表面轮廓分形维数计算方法的研究［J］.摩擦学学报，1997，17(4):354-362.

［5］季 旭，赵林，耿 雷，等.微细铣削加工表面形貌的分形特征［J］.黑龙江科技学院学报，2011，21(6):466-469.

［6］江炜，朱华，姬翠翠，等.磨合试验与表面形貌变化规律的分形表征［J］.山东科技大学学报(自然科学版)，2008，27(6):62-66.

［7］王海容，蒋庄德，尹燕玲.切削加工表面分形机理的研究［J］.机械科学与技术，2002，21(1):13-15.

［8］周俊杰，赵军.磨合过程摩擦表面分形参数研究［J］.汽车工程学报，2011，1(5):469-473.

［9］Kanga M.C.，Kima J.S.，Kim K.H..Fractal dimension analysis of machined surface depending on coated tool wear［J］.Surface＆Coatings Technology，2005，193:259-265.

［10］张喜燕，赵永庆，白晨光.钛合金及应用［M］.北京:化学工业出版社，2005.

［11］莱因斯C.，皮特尔斯M..钛与钛合金［M］.北京:化学工业出版社，2005.

［12］Ezugwa E.O.，Wang Z.M..Titanium alloys and their machinability—a review［J］.Journal of Materials Processing Technology，1997，68:262-274.

［13］Higuchi T.，Approach to an irregular time series on the basis of the fractal theory［J］.Physica D，1988，31:277-283.

［14］Simard P.，La Tavernier E.，Fractal approach for signal processing and application tothe diagnosis of cavitation［J］，Mechan.Syst.Signal Processing，2000，14:459-469.

［15］KupkováM.，Kupka M.，RudnayováE.，etal..On the use of fractal geometry methods for the wear process characterization［J］.Wear，2005，258:1462-1465.

［16］Zhu H.，Ge S.R.，Cao X.C.，etal..The changes of fractal dimensions of frictional signals in the running-in wear process［J］.Wear，2007，263:1502-1507.