一种关于目标与安全管道相对位置估算方法
孙艳英
(92941部队,辽宁葫芦岛125000)
一种关于目标与安全管道相对位置估算方法
孙艳英
(92941部队,辽宁葫芦岛125000)
针对靶场试验安全控制中目标与安全管道位置估算的实际需求,结合靶场实时数据处理要求,提出了利用滑动窗口技术,动态载入理论弹道数据,并采用折半查找和KNN查询相结合的思想实现了目标与理论弹道最近邻点查询,完成了飞行目标与理论规划航迹间的位置等参数偏差查询。利用区间估计原理,给出了目标与安全管道相对位置估算方法,解决了传统试验中无法对目标与管道边界的接近程度进行量化的问题。
靶场;安全管道;区间估计;k最近邻查询
安全控制是靶场测控系统的主要使命之一。靶场试验航区周围的重要保护目标逐年增多,为保障试验任务的安全顺利,要对飞行中的目标安全控制。安全管道是限制目标飞行的有效区域,在该区域内考核目标的飞行性能,若目标超出该管道区域必须及时对其控制,以保障航区设施的安全。在靶场进行的飞行试验中,安控指挥员根据目标与安全管道的位置关系、中心机提供的安全管道告警提示和目标遥测安控数判结果进行综合判断并完成对目标的安全控制。
在试验任务中,如果能实时计算目标与理论航迹间速度、位置等参数偏差大小,且当目标偏离理论航迹接近试验安全管道时,能对目标与安全管道的接近程度给出定量或定性的描述(如目标与管道之间的临界距离、临近时间等),不仅可以为安控指挥员提供直观准确的安控辅助判决依据,减少安控决策压力,增加决策时间,而且还可以对试验关键过程进行量化,为试验指挥员和首长试验决策提供详实的参考依据,提高靶场的安全控制能力。
为减少数据处理量,增加实时性,本文提出利用滑动窗口技术,实时载入目标的理论弹道数据和安全管道的边界数据,利用折半查找和连续k-最近邻查询算法相结合的办法,查询目标当前位置与理论弹道间的k最近邻域,在此基础上完成目标与理论弹道间的位置偏移、速度偏差估计;目标与安全管道间的临界距离及临近时间的区间估计等相关参数估算。
1 相关知识
1.1 KNN查询
数据流k最近邻(k-Nearest Neighbor,KNN)查询,是连续查找k个距离查询点最近的对象,并按从小到大的顺序排列,即为查询点的k个最近邻域[3-6]。
1.2 目标对象
目标对象可看作是欧式空间的一个点,其移动位置点可表示为:

式中:ti为目标飞行时间;(xi,yi,zi)为目标对象在ti时刻的空间直角坐标;(Li,Bi,Hi)为大地坐标;(vxi,vyi,vzi)为飞行速度;Ai为目标的飞行方向。
1.3 理论弹道
理论弹道是根据试验的要求事先计算好的,其计算步长为定长或变步长。在实时数据处理中,外场设备的数据帧频为d帧/s,为了在KNN查询中获得比较好的处理结果,将理论弹道加密为2d帧/s,其弹道点Di数据格式定义同格式Mi,存储在理论弹道数据文件中。
1.4 安全管道边界
安全管道边界是在综合考虑试验就位点和靶位点的误差、设备测量误差、数据处理误差,并充分考虑目标飞行性能和试验安全系数的基础上,将理论弹道按相应规则外扩,得到安全管道的左右边界,因而可按理论弹道文件数据帧频换算安全管道左、右边界数据文件。安全管道前端或末端为一条直线线段或2条折线线段,取直线或折线线段的端点数据分别存在管道上界和下界数据文件中。左、右管道边界数据格式
定义为
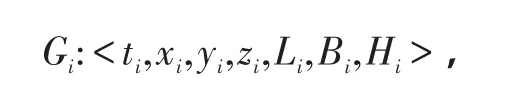
式中:(Li,Bi,Hi)为目标在ti时刻大地边界坐标;Hi=0;(xi,yi,zi)为该大地坐标转换后的空间直角边界坐标。
上、下管道边界数据格式定义为

地心空间直角坐标系(xi,yi,zi)和地心大地坐标系(Li,Bi,0)的关系为[2]:
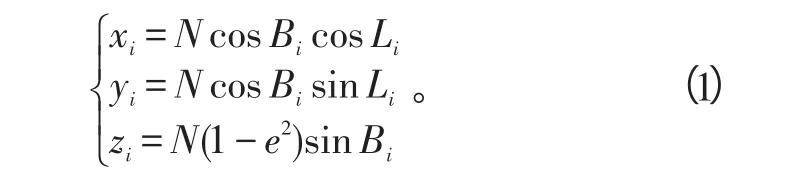
式(1)中:N为某点的卯酉圈曲率半径;e为椭球的第一扁心率。
1.5 目标空间距离
连续计算目标对象与查询数据对象间的空间距离,将计算的空间距离按从小到大的顺序排列。空间中的2个点mi和mj间的距离采用欧式距离计算公式:
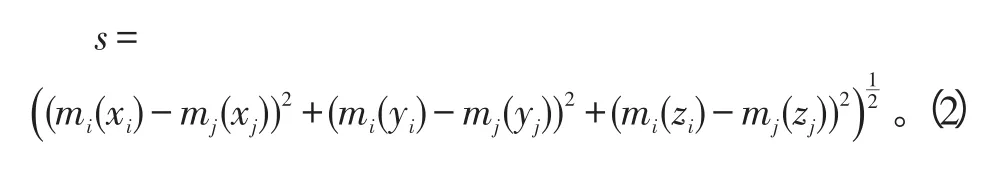
1.6 边界位置查询数据流
定义目标当前位置与管道边界保持最近的K个数据为

式(3)中:tk为目标飞行时间;sk为tk时刻目标距管道边界gk的距离;Tk为tk时刻目标与管道边界gk的临近时间;vk为tk时刻目标的飞行速度;Ak为tk时刻目标的飞行方向;Rk为目标与理论弹道的航偏距;gk为边界位置,gk=0为上边界,gk=1为左边界,gk=2为右边界,gk=3为下边界。
2 查询算法
2.1 算法流程
外场测控数据经过野点剔除、数据平滑、数据关联、数据定位等相关处理后,得到目标对象的空间位置和有关的运动参数[7-9]。
本文引用KNN查询思想,结合折半查找方法,在理论弹道上查询经测控数据解算的目标对象的最近邻点,将查询的最近邻点位置按目标与理论弹道位置判断方法和某种映射关系与管道边界相对应,再根据目标飞行速度和飞行方向计算目标当前位置与理论弹道间的参数偏差、目标与管道相应边界的接近程度等相关参数的估算。
算法流程如图1所示。
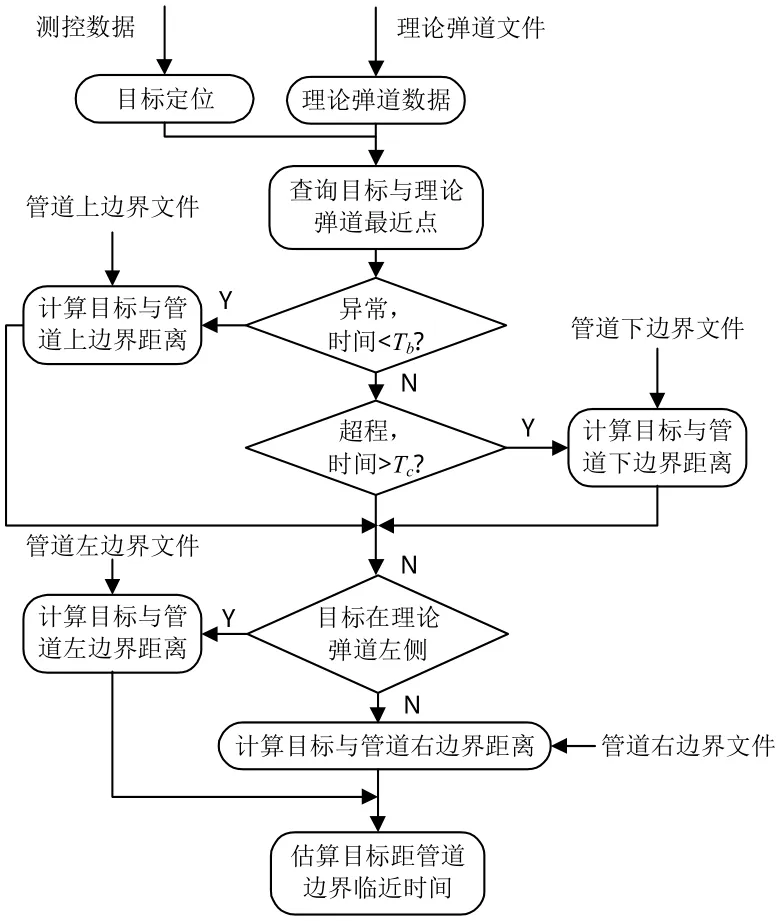
图1 算法流程图Fig.1 Flow chart of algorithm
2.2 目标与理论弹道最近邻点查询算法
因理论弹道数据的文件较大,采用1次读入1个数据窗口的方法读取理论弹道,数据窗口的长度设定为n。为保证数据处理的实时性,采用3个长度为n的数据窗口CP、CI、CN,分别为历史数据窗口,当前数据窗口和下一数据窗口,各窗口中数据相邻。采用折半查找和KNN算法查询目标与理论弹道最近邻点,算法步骤如下。
Step1:比较目标当前点M分别与3个窗口中心点的距离sCP、sCI、sCN,求最小距离smin=min{sCP,sCI,sCN};
Step2:计算距离为smin的窗口C的左右边缘点CL、CR与M点的距离sL、sR并与smin比较,重新计算最小距离smin=min{smin,sL,sR};
Step3:若smin=sL且窗口C=CP,此时历史数据窗口最左端数据位置距目标距离最近,则更新数据窗口CN=CI、CI=CP,从理论弹道文件中重新读入窗口CP左边缘点CPL起的前n组数据至窗口CP,转Step1;
Step4:若smin=sR且窗口C=CN,则更新数据窗口CP=CI、CI=CN,从理论弹道文件中继续读入窗口CN右边缘点CNR起的n组数据至窗口CN,转Step1;
Step5:n1=n/2;若([n1=n1/2]〉2k),以smin为中心点,循环计算其左右间距为n1的点与M点的距离sL和sR,最小距离smin=min{smin,sL,sR};
Step6:以smin为中心,计算其前后各k/2个点与M点的距离,并按从小到大的顺序排列。最小值点可近似看作理论弹道与目标当前位置的最近点Dm。
2.3 目标与理论弹道位置偏差查询
2.3.1 航向角计算
利用理论弹道上求出的最近点Dm(Lm,Bm)与其前一时刻的点D′(L′,B′)实时计算目标的航向角,判断目标的飞行方向。算法步骤如下。
Step1:若Lm〈L′时,目标当前理论航向角

Step2:若Lm〉L′时,目标当前理论航向角

Step3:若Lm=L′时,当B〉B′,航向角A=π;B〈B′,航向角A=0。
2.3.2 目标与理论弹道位置判断
由当前理论航向角A大小及目标M(LM,BM)与理论弹道位置关系,可判断目标与理论航迹的位置关系。目标位置与航向角关系如图2所示。

图2 目标位置与航向角示意图Fig.2 Schematic diagram of target position and course angle
对于图2中所示理论弹道D1,航向角A1位于第一象限和第二象限,由B=L和B=-L组成的夹角区域。目标在点M1(LM1,BM1)位置与理论弹道对应的最近邻点为D1(LD1,BD1),目标在点M2(LM2,BM2)位置与理论弹道对应的最近邻点为D2(LD2,BD2)。可以推出,当BM1≥BD1,目标位于理论弹道左侧;当BM2〈BD2,则目标位于理论弹道右侧。
对于图2中所示理论弹道D2,航向角A2位于第一象限和第四象限,由B=L和B=-L组成的夹角区域。目标在点M3(LM3,BM3)位置与理论弹道对应的最近邻点为D3(LD3,BD3),目标在点M4(LM4,BM4)位置与理论弹道对应的最近邻点为D4(LD4,BD4)。可以推出,当LM3≤LD3,目标位于理论弹道左侧;当LM4〉LD4,则目标位于理论弹道右侧。
同理可判断航向角为A3和A4的目标与理论弹道的位置关系。
2.3.3 侧向偏差
计算Dm点与M点在大地椭球面上的投影点,求出投影点间的距离RZ,近似看作M点与理论弹道的侧向偏差。
令Dm点与M点大地坐标高度为0,由式(1)计算Dm点和M点在大地椭球面上的投影的空间直角坐标,再由式(2),即可求出M点与理论弹道的侧向偏差RZ。
一般定义目标位于理论弹道左侧时航偏距为正,右侧时航偏距为负。
2.3.4 速度偏差
根据理论弹道各点的飞行速度,可实时计算目标的理论飞行速度均值,与解算的目标实际飞行速度均值相比较,可以判断目标飞行速度的快慢,量化目标实际飞行速度与理论航速之间的偏离程度。
航速均值计算公式为[1]

3 目标与管道边界位置估算
3.1 管道边界位置判断
利用Dm点的时间tm和目标与理论弹道位置关系,可判断目标与管道边界的位置关系。已知理论弹道初始位置时间Tb和超程位置时间Tc,算法步骤如下。
Step1:若tm〈Tb,目标反向飞行,如果目标位于理论弹道左侧,则计算目标与左边界和上边界距离,否则计算目标与右边界和上边界距离;
Step2:若tm〉Tc,如果目标位于理论弹道左侧,则计算目标与左边界和下边界距离,否则计算目标与右边界和下边界距离;
Step3:若Tb〈tm〈Tc,目标位于理论弹道左侧,则计算目标与左边界距离,否则计算目标与右边界距离。
3.2 目标与管道上下边界距离计算
以上(下)边界文件存储的相邻点间的连线所构成1条或2条线段,计算目标当前点到线段的距离即为目标到管道的边界上(下)边界距离[9]。若该边界目标位于理论弹道左侧,计算目标当前点与第1条线段间的距离;否则,计算目标当前点与第2条线段间的距离。
3.3 目标与管道左右边界距离计算
若目标位于理论弹道左(右)侧,根据理论弹道与管道左右边界数据的映射性,只须查询左(右)边界数据文件中时间为tm的点Gm,计算Gm点与目标M点间的距离,该值可作为目标与管道边界的最近临界距离DBM-1。由于目标并非沿与理论弹道垂直的方向飞行,所以目标与管道左右边界可用区间数形式表示[10-11]。无论目标趋向或远离边界方向,右区间距离DBM-2均采用下述步骤近似计算。
Step1:按2.3.1节方法计算目标实时运动方向AM;
Step2:计算与理论航向AL夹角
3.4 目标距管道边界临界时间估计
目标运动过程中,每一时刻的飞行速度并不相同,可采用区间估计的方法[12]先估计导弹的飞行速度区间;然后,在此基础上对临界时间进行估计。
对于每一时刻目标的飞行速度历史记录值vk,假设目标飞行速度样本服从正态分布,以当前时刻前一小段区间[tk1,tk2]为样本区间,求样本飞行速度均值v¯、样本方差

根据目标与管道的距离估计区间和速度估计区间,求取目标与管道的临界时间估计区间为
4 仿真实例
仿真生成1条理论弹道和异常数据。理论弹道数据间隔0.1 s,异常数据间隔1 s,将理论弹道数据左右任意外扩5km,生成安全管道左右边界,采用上述方法,用VC++编程实现。目标与管道位置计算结果如表1所示。

表1 目标与管道位置计算结果Tab.1 Calculate results for target and pipeline position
如果将理论弹道数据加密,其数据计算结果将更为准确。
5 结论
安全控制是靶场试验的一个重要环节。在试验中为指挥员提供丰富的辅助决策信息是提高靶场安全控制和试验指挥自动化能力的要求。本文给出了目标与安全管道位置估算方法,对试验目标与安全管道的接近程度进行了量化,实现了飞行目标与理论规划航迹偏差程度的查询,可为试验指挥员提供安控辅助决策依据。
[1] 吴翊,李永乐,胡庆军.应用数理统计[M].长沙:国防科技大学出版社,2005:20-25. WU YI,LI YONGLE,HU QINGJUN.Application of mathematical statistics[M].Changsha:National University of Defense Technology Press,2005:20-25.(in Chinese)
[2] 孔祥元,郭际明,刘宗泉.大地测量学基础[M].武汉:武汉大学出版社,2001:36-37. KONG XIANGYUAN,GUO JIMING,LIU ZONGQUAN.The fundamentals of geodesy[M].Wuhan:Wuhan University Press,2001:36-37.(in Chinese)
[3] 王考杰,郑雪峰,宋一丁,等.面向轨迹数据流的KNN近似查询[J].计算机工程,2011,37(16):17-20. WANG KAOJIE,ZHENG XUEFENG,SONG YIDING,et al.KNN approximate query for trajectory data stream[J].Computer Engineering,2011,37(16):17-20.(in Chinese)
[4] 刘大峰,戴宁,孙全平,等.基于测量步距的散乱点云k近邻搜索算法[J].中国机械工程,2008,19(4):414-418. LIU DAFENG,DAI NING,SUN QUANPING,et al.Algorithm based on scanning step for finding all k-nearest neighbors of scattered points[J].China Mechanical Engineering,2008,19(4):414-418.(in Chinese)
[5] 廖巍,吴秋云,陈宏盛,等.基于扩展时空距离度量的连续k近邻查询方法[J].国防科技大学学报,2007,29(1):81-85. LIAO WEI,WU QIUYUN,CHEN HONGSHENG,et al. Continuous k-nearest neighbor queries based on extended spatio-temporal distance metrics[J].Journal of National University of Defense Technology,2007,29(1):81-85.(in Chinese)
[6] 胡云,施琚,王崇骏,等.基于全局最近邻的离群点检测算法[J].计算机应用,2011,31(10):2778-2781. HU YUN,SHI JU,WANG CHONGJUN,et al.Outlier detection algorithm based on global nearest neighborhood [J].Journal of Computer Applications,2011,31(10):2778-2781.(in Chinese)
[7] 贺明科,王正明,朱炬波.多传感器目标跟踪的实时剔野方法[J].宇航学报,2002,23(6):34-37. HE MINGKE,WANG ZHENGMING,ZHU JUBO.Reahime outliers detection in multi-sensor target traching[J]. Journal of Astronautics,2002,23(6):34-37.(in Chinese)
[8] 刘利生.外弹道测量数据处理[M].北京:国防工业出版社,2002:270-302. LIU LISHENG.Data processing of exterior trajectory measurement[M].Beijing:National Defense Industry Press,2002:270-302.(in Chinese)
[9] 杨得国,王明海,王立安.巡航导弹航迹与威胁区相对位置判定方法[J].四川兵工学报,2011,32(8):10-13. YANG DEGUO,WANG MINGHAI,WANG LIAN.A study of estimation on relative position between path and threat for cruise missil[J].Journal of Sichuan Ordnance,2011,32(8):10-13.(in Chinese)
[10] 万树平.目标威胁评估的区间数方法[J].计算机工程与应用,2009,45(6):32-34. WAN SHUPING.Interval number method for object threat assessment[J].Computer Engineering and Applications,2009,45(6):32-34.(in Chinese)
[11] 徐泽水.基于可能度和误差分析的区间数互补矩阵排序法[J].解放军理工大学学报,2003,4(2):96-98. XU ZESHUI.Priority method based on possibility and error analysis for interval number complementary judgment matrix[J].Journal of PLA University of Science and Technology,2003,4(2):96-98.(in Chinese)
[12] 张大巧,刘刚,鲜勇,等.多航迹交叉的时空判断方法研究[J].计算机仿真,2010,27(1):76-79. ZHANG DAQIAO,LIU GANG,XIAN YONG,et al.Research on time-space judgment method of multi-route intersection[J].Computer Simulation,2010,27(1):76-79.(in Chinese)
An Evaluating Method of Relative Position between Target and Safety Pipeline
SUN Yan-ying
(The 92941stUnit of PLA,Huludao Liaoning 125000,China)
Aiming to the actual demand of position evaluating between target and safety pipeline on safety control in range test,combining with the real-time data processing,it put forward that using of the sliding window technique,dynamica loading theoretical trajectory data and using technique of binary search and KNN query to realize KNN query between target and theoretical trajectory.Position deviation query between target and theoretical trajectory was finished.Evaluating method of relative position between target and safety pipeline was given based on the principle of interval estimation.The problem of close degree between target and safety pipeline that could not be quantitative analysis in the traditional interval test was resolved.
range;safety pipeline;interval estimation;k Nearest Neighbor(KNN)query
V 557.1;TP311
A
1673-1522(2014)04-0306-05
10.7682/j.issn.1673-1522.2014.04.002
2014-03-12;
2014-05-12
孙艳英(1971-),女,高工,硕士。

