一种基于DFT的高精度载波频偏估计算法
朱乾坤,许阳,刘东鑫,于德海
(1.海军航空工程学院训练部,山东烟台264001;2.91372部队,上海200436)
一种基于DFT的高精度载波频偏估计算法
朱乾坤1,许阳2,刘东鑫1,于德海1
(1.海军航空工程学院训练部,山东烟台264001;2.91372部队,上海200436)
针对无线数字通信中的载波频率同步问题,提出一种新的载波频偏估计算法。利用离散傅里叶变换(DFT)内插技术,在较大频偏范围内估计出载波频偏,并且在估计精度上相对于DFT法有了很大的提高。这种算法不需要增加DFT数据长度,适合突发通信方式。进行了Monte Carlo仿真实验,仿真结果表明新算法不仅具有宽的估计范围,还具有高的估计精度。
载波同步;频偏估计;突发同步;DFT算法
由于突发通信的分组数据是在瞬间突然发送出数据,在很短的时间,频率变化快,具有隐蔽性和难以拦截的特点,被广泛使用在短波无线电通信,突发通信成为现代通信的一个热点问题。而在无线通信中,由于不可避免地受到多普勒频移和本地载波误差的影响,接受端的本地载波频率会发生偏移,致使接收信号的载波和发送端的载波存在一定的误差,如果不消除这种误差,将会严重影响通信系统的相干解调,使得通信系统的性能退化,所以接收机必须对频偏进行补偿达到载波同步[1-4]。
文献[5]给出了在高斯白噪声中对正弦波信号频率进行最大似然估计(MLE)算法,估计误差的方差达到了克拉美-罗界,因而是最优估计。由于MLE算法计算量大,难以实时进行处理,于是学者们提出了很多基于最大似然估计的简化算法。Kay在1989年提出了经典的kay算法[6]。相对于最大似然估计(MLE)算法,kay算法的计算复杂度有了很大简化,但是存在较高的信噪比门限(6 dB),当接收端信噪比小于该门限时,性能急剧恶化,没有达到工程应用的要求。而针对kay算法高信噪比门限的缺点,文献[7]提出了L&R算法。L&R算法也是基于最大似然算法的简化算法,具有很低信噪比门限(-10 dB),完全能满足工程应用要求,但频偏估计范围过窄,也不适合运用于工程上。文献[8]提出了M&M算法。M&M算法既具有低的低信噪比门限,又能估计很大的频偏,但是复杂度太高,同步过慢,不利于实时处理。
基于最大似然估计的算法共有的一个缺陷就是计算复杂,同步速度慢。而基于离散傅里叶变换(DFT)的谱估计方法,由于在实际中可通过快速傅里叶(FFT)实现,运算量小,得到广泛应用。但由于DFT算法存在栅栏效应和能量泄漏,在样本长度较小时估计误差较大,为了提高准确性,必须需要长的样本数量N,这就局限了DFT算法的应用。针对DFT算法估计误差较大的缺陷,文献[9]提出了Rife算法。该算法先对接收信号进行FFT变换,然后利用最大谱线和次大谱线来确定真实的频率位置。Rife算法相对于DFT算法性能得到了改善,且复杂度不高,易于硬件实现。但是对小频偏不敏感,精度不高,存在短的数据长度N精度不高,长的数据长度N复杂度太高的问题,在实际工程中并不适用。对此,文献[10-13]提出了许多有效的改进方法,但是复杂度都偏高。本文提出了一种基于离散傅里叶变换的新算法,利用最大幅值2侧的点进行估计,避免了单纯用DFT估计所出现的栅栏效应和能量泄漏,并且通过比较频谱搬移后的最大幅值|B′k|和搬移前的最大幅值|Bk|,来判断δ正负号是否取反。本文算法克服了RIFE算法FFT量化频率附近时误差较大的缺点,使得新算法在估计性能上相对于RIFE算法和FFT算法有了明显改善。这种算法不需要增加DFT数据长度,适合突发工作方式。
1 信号模型
本算法采用MPSK调制方式,在高斯白噪声信道下进行传输,高斯白噪声的双边谱密度为N0/2,采样时满足Nyquist准则,已经完成信道均衡,消除了码间干扰。并假定接受端进行载波同步之前已经进行精确的定时同步,不存在定时偏差。假设接受端的载波频率相对于发送端的载波频率的频率偏差为fe,则接收端基带信号
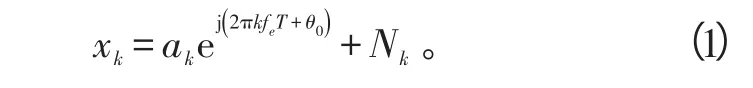
式(1)中:ak是所要接受的信号,对于MPSK信号,可以表示为

T是符号周期;θ0是载波相位;θ0在观测数据长度N内是确定的未知量;fe是需要估计的载波频偏;Nk是加性高斯白噪声,其均值为0且方差为σ2[14]。实际上由于表示ak的复数共轭),于是可以定义,即得到:

2 算法分析
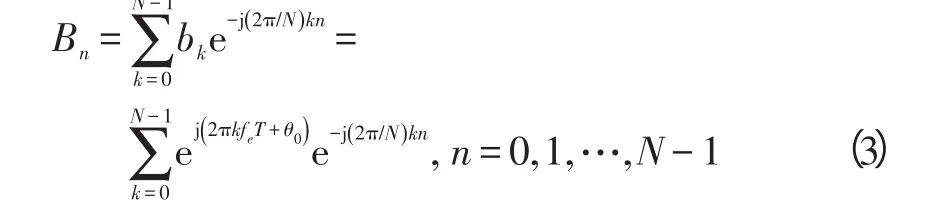
通过对式(3)的进行公式变换得到[15]:

得到Bn的幅度为:

当0≤n≤N/2时,如果0≤feT≤0.5,那么-π/2≤(πn-πfeTN)/N≤π/2。在(πn-πfeTN)/N趋于0时,故式(5)近似等于:

即|Bn|近似为sinc函数。当πn-πfeTN为0时,|Bn|为 N。由于n为整数,πn-πfeTN不一定能取到0。而根据sinc函数性质,πn-πfeTN越接近于0,|Bn|就越大,假设n=k时,|Bn|为最大,则πk-πfeTN必然接近于或等于0,且此时k〈N/2。令δ=πk-πfeTN,则|δ|满足|δ|〈π/2,如能估计δ,则fe=(πk-δ)/(TNπ)。
当N/2≤n≤N时,如果-0.5≤feT≤0,那么-π/2≤(π(n-N)-πfeTN)/N≤π/2。
在(π(n-N)-πfeTN)/N趋于0时,得到故式(5)近似等于|Bn|≈N sin c(π(n-N)-πfeTN)。同理存在n=k使得|Bn|为最大,则π(k-N)-πfeTN必然接近于或等于0,且此时k〉N/2。令δ=π(k-N)-πfeTN,则|δ|必然满足|δ|〈π/2,如果能够估计出δ,则fe=(π(k-N)-δ)/(TNπ),即:
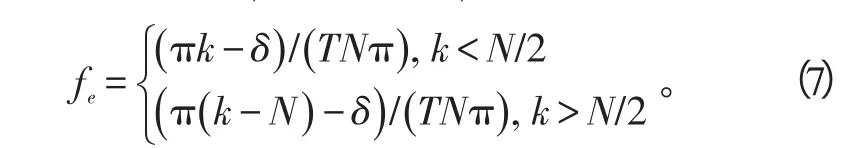
所以,算法关键在于估计δ。又因为:

做|Bk-1|与|Bk+1|的比值,于是得到

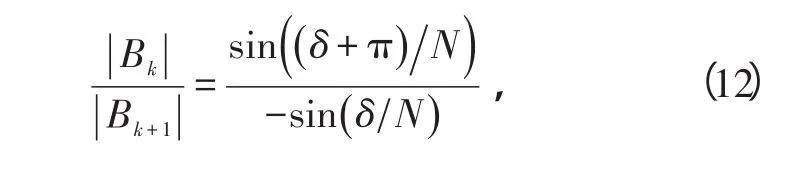
则得到
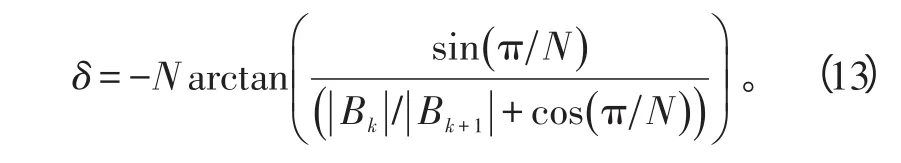
而当|Bk-1|>|Bk+1|时,

则得到
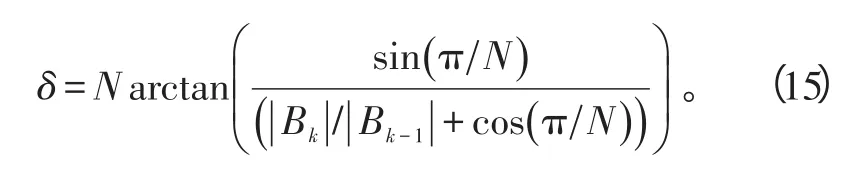
还可以通过|Bk+1|、|Bk|、|Bk-1|中最大与最小值求得δ,此为方案2;通过|Bk+1|、|Bk|、|Bk-1|中较小的2个求得δ,此为方案3。由于实际中都存在噪声,3种方案的性能有区别。仿真实验证明,方案1总体性能最好,如图1所示。图1是SNR为10 dB、归一化频偏范围0.04~0.08时3种方案的性能比较图。
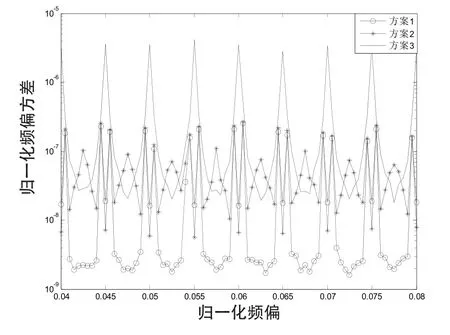
图1 3种方案性能比较图Fig.1 Performance comparasion chart for 3 schemes
实际中,由于噪声的影响使得|Bk-1|与|Bk+1|的大小发生变化,从而导致δ正负方向性错误,进而导致频偏估计误差变大。对接收信号bk进行频谱搬移,,对b′k做DFT变换,得到,其最大幅值,必然满足|B′k|≥|Bk|,所以若|B′k|〈|Bk|,就可以判定δ正负号已取反。
如果得到|B′k|〈|Bk|,改变δ正负号,采用方案1,当|Bk-1|<|Bk+1|时,δ>0,通过|Bk-1|与|Bk|得到δ为

当|Bk-1|<|Bk+1|时,δ<0,此时通过|Bk+1|与|Bk|得到δ为
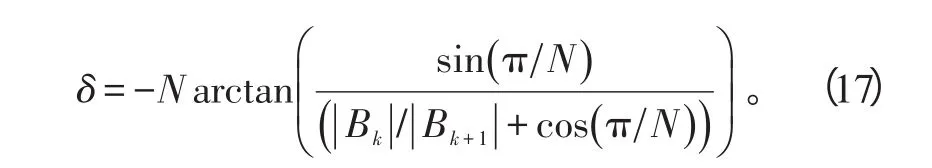
采用方案2,当|Bk-1|<|Bk+1|时,δ>0,通过|Bk+1|与|Bk|得到δ为

当|Bk-1|<|Bk+1|时,δ<0,此时通过|Bk-1|与|Bk|得到δ为
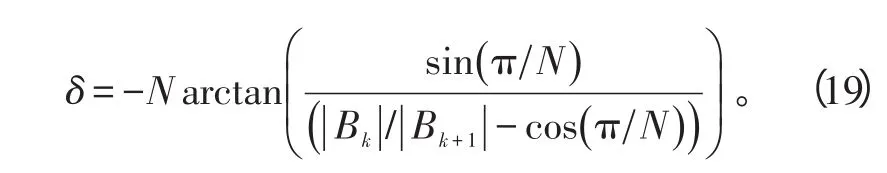
图2是SNR为-5 dB、归一化频偏范围0.04~0.08时2种方案的性能比较图。由图2可以看出,方案1的性能要比方案2的好,因而采用方案1。
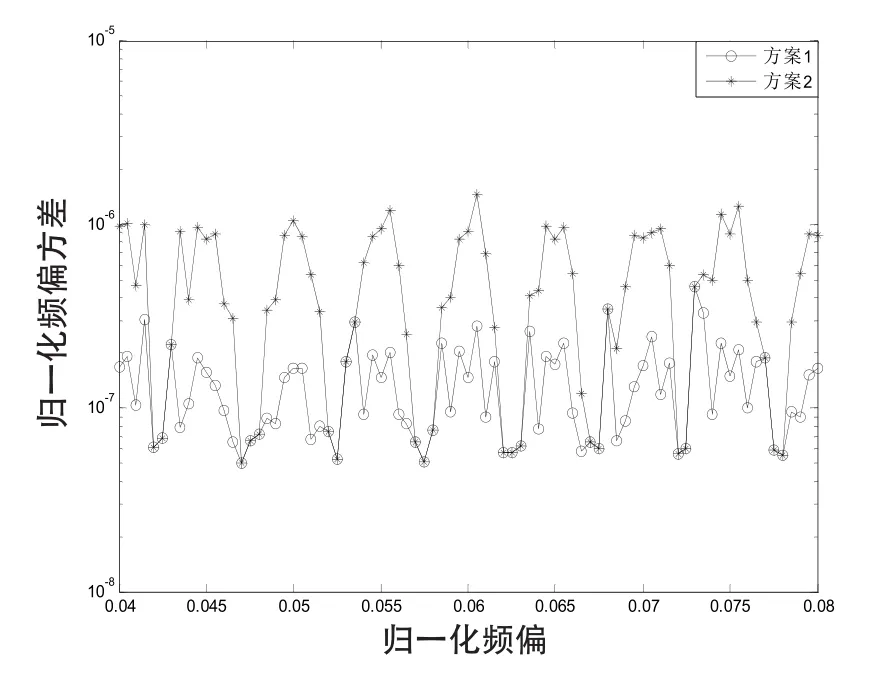
图2 2种方案性能比较图Fig.2 Performance comparasion chart for 2 schemes
估计出δ后,代入fe=(πk-δ)/(TNπ),即估计出载波频偏。综上本算法步骤:
1)对接收信号bk做FFT变换,并搜索得到得|Bk-1|、|Bk+1|、|Bk|(|Bk|是最大幅值);
2)比较|Bk-1|和|Bk+1|。如果|Bk-1|<|Bk+1|,则δ< 0,通过|Bk+1|与|Bk|,根据式(14)估计出δ值;如果|Bk-1|>|Bk+1|,则δ>0,通过|Bk-1|与|Bk|,根据式(15)估计出δ值;
3)对bk进行频谱搬移,得到b′k=bkexp(-2π(δ π) T),做FFT变换得到|B′n|,搜索得到最大幅值|B′k|。如果|Bk-1|<|Bk+1|,则δ>0,通过|Bk-1|与|Bk|,由式(17)估计出δ值;如果|B′k|<|Bk|,当如果|Bk-1|>|Bk+1|,则δ<0,通过|Bk+1|与|Bk|,根据式(17)估计出δ值。
4)通过式(7)估计出频偏。
3 建模仿真与分析
通过Matlab对本算法进行蒙托卡罗仿真,主要在估计范围和估计性能2方面进行分析,并与FFT算法、Rife算法进行比较。本文仿真实验采用8PSK调制方式,观测数据长度N为128,并且用归一化频偏估计误差来衡量算法的估计精度,并定义为

3.1 估计范围
由DFT的性质可以得到[6],载波频偏fe〈1/2T时,本算法时适用的;当采样速率fs=1/T时,本算法的估计范围为|fe|〈fs/2。图3是输入信噪比为-5、0、5、10 dB,归一化频偏feT在-0.5~0.5变化时,算法估计方差随频偏变化的曲线图。由图3可以看出在低信噪比和高信噪比下,本算法的估计范围都能达到fs/2,并且性能很好。这验证了理论上估计范围为|fe|〈fs/2。
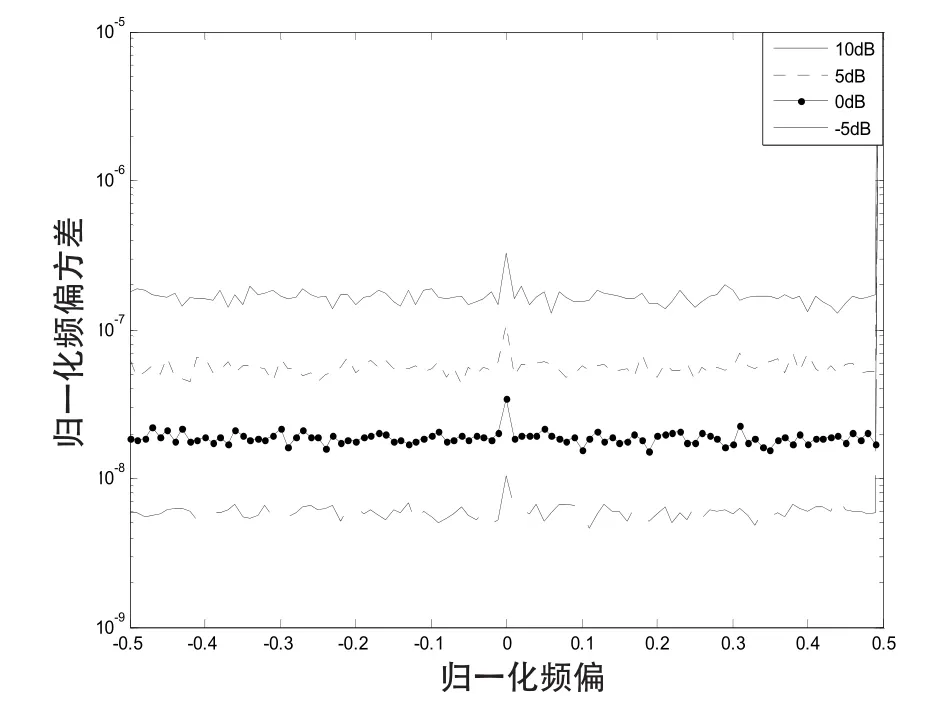
图3 不同信噪比下估计方差随频偏的变化曲线Fig.3 Variance chart for estimation mean square error versus frequency offset under different SNR
3.2 估计性能
图4是在不同信噪比下对于不同频偏值,归一化频偏误差方差与克拉美-罗界之间的比较。
克拉美-罗界的理论值是

式中,SNR是信噪比,满足SNR=A2/(2σ2。)
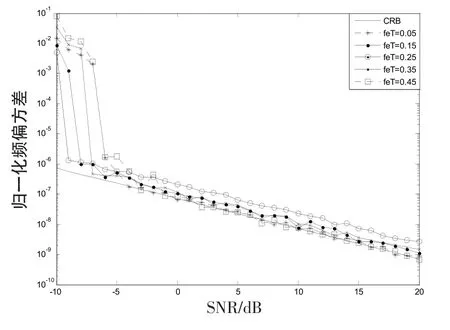
图4 不同频偏下频偏方差随信噪比的变化曲线Fig.4 Variance chart for frequency offset versus SNR under different frequency offset
由图4看出,在频偏估计范围内,在低于某个信噪比门限下,性能急剧恶化。这是由于当信噪比过低时,由于噪声的影响,不能正确判断出最大幅值的位置,致使估计出现较大偏差。当信噪比大于信噪比门限时,频偏方差接近于克拉美-罗界,性能很好。本算法的信噪比门限能达到-5 dB完全满足实际需要。
3.3 与经典算法性能比较
图5是在信噪比为-5 dB下,归一化频偏feT在0.04~0.08范围内新算法,FFT算法及RIFE算法估计方差随频偏变化曲线图。
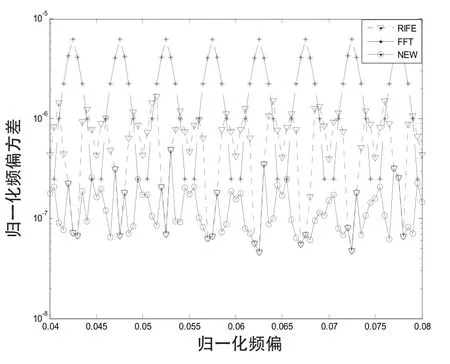
图5 估计方差随频偏变化曲线图Fig.5 Variance chart for estimation mean square error versus frequency offset
从图5中可以看出,新算法在性能上相对于FFT算法有了很大提高。这是因为FFT算法只是利用最大幅值点估计频偏,存在能量泄露和栅栏效应,估计性能很差,新算法不仅利用到最大幅值点估计频偏,还通过最大幅值点2侧的点来改善其性能,克服了FFT算法能量泄露和栅栏效应,使得估计性能有很大改善。
新算法与RIFE算法相比,在某些频偏范围内性能有了明显的改善。这是因为,对于RIFE算法,当信号的真实频率处于两相邻量化频率之间的中心区域时,Rife算法精度很高;但是在FFT量化频率附近时,由于噪声的影响,会导致次最大幅度的选取错误,致使RIFE算法比FFT算法估计误差要大得多。而新算法通过比较频谱搬移后的最大幅值|B′k|和搬移前的最大幅值|Bk|,来判断δ正负号是否取反,克服了RIFE算法FFT量化频率附近时误差较大的缺点。
4 结论
本文提出了一种在突发通信中利用离散傅里叶变换(DFT)内插技术的载波频偏估计算法。这种算法通过DFT变换可以很好地对频率偏移进行估计,而没有增加数据长度。当信噪比大于信噪比门限(-5 dB)时,载波频偏估计精度接近克拉美-罗界,而估计范围可以达到±0.5的符号速率。新算法相对于FFT算法和RIFE算法估计精度上有了很大改善,相比于其他几种传统算法,对于频偏的估计,在精度、范围可与M&M算法相比拟,而复杂度要低得多,并且新算法所使用的FFT技术已经很成熟,相关的硬件实现都比较容易。
[1] JOHN G PROAKIS.Digital communications[M].4th ed. Beijing:Publishing House of Electronics Industry,2006:333-372.
[2] 孙令明,张爱春,孙晓东.通讯信号波特率的盲估计[J].长春理工大学学报:自然科学版,2010,33(3):75-79. SUN LINGMING,ZHANGAICHUN,SUN XIAODONG. Blind estimation of baud-rate of communication signals [J].Journal of Changchun University of Science and Technology:Natural Science Edition,2010,33(3):75-79.(in Chinese)
[3] 封彬,赵艳丽,刘剑锋,等.卫星通信中基于Gardner算法的抗载波偏差法[J].电子技术应用,2014,40(4):103-105. FENG BIN,ZHAO YANLI,LIU JIANFENG,et al.Anticarrier deviation's method based on Gardner algorithm in satellite communication[J].Application of Electronic Technique,2014,40(4):103-105.(in Chinese)
[4] 孙锦华,王雪梅,吴小钧.短突发系统数据辅助载波同步的导频设计[J].电子与信息学报,2014,36(3):669-675. SUN JINHUA,WANG XUEMEI,WU XIAOJUN.Pilot esign of ata-aided arrier ynchronization for hort urst ransm ission[J].Journal of Electronics&Information Technology,2014,36(3):669-675.(in Chinese)
[5] RIFE D C,BOORSTYN R R.Single-tone parameter estimation from discrete-time observation[J].IEEE Transactions on Information Theory,1974,20(5):591-598.
[6] KAY S.A fast and accurate single frequency estimator[J]. IEEE Transactions on Acoustic Speech Signal Process,1989,37(12):1987-1990.
[7] LUISE M,REGGINNAINI R.Carrier frequency recovery in all digital modems for burst mode transm issions[J]. IEEE Transactions on Coieations,1995,COM-43(2):1169-1178.
[8] MENGALI U,MORELLI M.Data-aided frequency estimation for burst digital transm ission[J].IEEE Transactions on Communication,1997,45(1):23-25.
[9] RIFE D C,VINCENT G A.Use of the discrete fourier transform in the measurement of frequencies and levels of tones[J].Journal of Bell System Technology,1970,49:197-228.
[10] 刘渝.快速高精度正弦波频率估计综合算法[J].电子学报,1999,27(6):126-128. LIU YU.A fast and accurate single frequency estimator synthetic approach[J].Acta Electronica Sinica,1999,27(6):126-128.(in Chinese)
[11] 周喜庆,赵国庆,王伟.实时准确正弦波频率估计综合算法[J].西安电子科技大学学报,2004,31(5):657-660. ZHOU XIQING,ZHAO GUOQING,WANG WEI.A realtime and accurate sinusoidal frequency estimation synthetic approach[J].Journal of Xidian University,2004,31(5):657-660.(in Chinese)
[12] 王旭东,刘渝,邓振淼.基于修正Rife算法的正弦波频率估计及FPGA实现[J].系统工程与电子技术,2008,30(4):621-624. WANG XUDONG,LIU YU,DENG ZHENMIAO.Modified Rife algorithm for frequency estimation of sinusoid and implementation in FPGA[J].Systems Engineeringand Electronics,2008,30(4):621-624.(in Chinese)
[13] 张瑞华,欧阳缮,周德新.一种新的基于LMP准则的自适应正弦波频率估计算法[J].信号处理,2003,19(2):153-156. ZHANG RUIHUA,OUYANG SHAN,ZHOU DEXIN.A new adaptive sinusoid frequency estimation algorithm based on least mean p-power criterion[J].Signal Processing,2003,19(2):153-156.(in Chinese)
[14] 彭华,李静,葛临东.一种非判决辅助前向结构载波频差估计方法[J].电子学报,2001,29(7):984-986. PENG HUA,LI JING,GE LINDONG.Non-decision-aided feed forward carrier frequency offset estimator[J].Acta Electronica Sinica,2001,29(7):984-986.(in Chinese)
[15] WANG Y P E,OTTOSSON T.Initial frequency acquisition in W-CDMA[C]//IEEE Proceedings of 50th Vehicular Technology Conference.Sw itzerland:Ericsson Inc.,1999,2:1013-1017.
A High-Precision Carier Frequency Offset Estimation Algorithm Based on DFT
ZHU Qian-kun1,XU Yang2,LIU Dong-xin1,YU De-hai1
(1.Department of Training,NAAU,Yantai Shandong 264001,China; 2.The 91372ndUnit of PLA,Shanghai 200436,China)
According to the problem for the carrier frequency synchronization in wireless digital communications,a new carrier frequency offset estimation algorithm was proposed.Using the discrete fourier transform(DFT)interpolation technique, the carrier frequency offset was estimated in a wide frequency offset range,and the estimation accuracy was greatly improved,relative to the DFT.This algorithm does not increase the DFT data length for burst work.Finally,a Monte Carlo simulation experiment was done,and the simulation results showed that the new algorithm not only had a wide range of estimates,but also had high estimation accuracy.
carrier synchronization;frequency offset estimation;burst synchronization;the DFT algorithm
TN925
A
1673-1522(2014)04-0329-06
10.7682/j.issn.1673-1522.2014.04.007
2014-03-24;
2014-05-05
朱乾坤(1965-),男,副教授,硕士。

