基于MILP的多无人机对敌防空火力压制

颜骥，李相民，刘波，刘立佳

（1.海军航空工程学院a.研究生管理大队；b.兵器科学与技术系，山东烟台264001；2.光电控制技术重点实验室，河南洛阳471009）

基于MILP的多无人机对敌防空火力压制

颜骥1a，李相民1b，刘波2，刘立佳1a

（1.海军航空工程学院a.研究生管理大队；b.兵器科学与技术系，山东烟台264001；2.光电控制技术重点实验室，河南洛阳471009）

建立了基于混合整数线性规划（Mixed Integer Linear Program，MILP）的多无人机编队对敌防空火力压制协同任务分配模型，以0-1决策变量表征无人机—任务指派关系，引入连续时间决策变量来表示任务的执行时间，并通过对决策变量之间的线性等式和不等式的数学描述，建立无人机之间和无人机执行任务之间合理的协同约束关系。采用商用软件CPLEX对模型求解，仿真验证了模型的合理性。

对敌防空火力压制；任务分配；混合整数线性规划；多机协同

当代军事对抗越来越依赖于空中力量的使用，近几次局部战争表明，对敌防空火力压制（Ssuppression of Enemy Air Defenses，SEAD）是空中军事力量的关键，并发挥日益重要的作用[1]。SEAD是一种以破坏和（或）干扰的方式使敌地基防空（主要是面对空导弹防御系统和防空火炮系统）能力失效，或暂时失效的活动。许多军事平台，弹药和作战行动都可用于对敌防空火力压制活动，但主要是通过使用电子战飞机在信号层或信息层对敌地面防御系统压制或欺骗干扰，使用空对地攻击战斗机或SEAD飞机携带反辐射武器摧毁敌地面防御系统实体，以最大限度摧毁敌目标的同时提高我方空中力量生存概率[2]。现代导弹防御系统的移动性、隐蔽性、高命中精度及雷达预警系统与发射装置分离等特性，使利用常规远程巡航导弹和有人战斗机执行对敌防空火力压制任务变得低效能和高风险。无人机因轻便、智能、无需人类飞行员驾驶等特性，越来越多地用于执行危险复杂的军事任务[2]。文献[3]通过改进的Voronoi图为无人战斗机规划安全路径，以提高其生存概率。文献[4]采用混合整数线性规划方法来求解具有时序约束的多无人机多任务分配问题，但其需要枚举所有航路点间的最短路径及所有可行路径的组合以满足时间约束。文献[5]采用编码方式为双染色体的矩阵遗传算法对该问题求解，但编码方式复杂且在表现任务时间约束上不直观。文献[6]采用混合重分配策略和混合细菌觅食算法来解决动态环境下的多UCAV协同任务分配问题。文献[7]设计了基于相邻局部通信的分布式拍卖算法，实现了多无人机协同任务分配问题的优化求解，考虑了任务时序性要求，但缺乏对无人机之间时间约束的考虑。文献[8]采用合同网实现任务执行过程中的任务分配，但各无人机间的通信复杂，并缺乏对算法实时性的分析。文献[9-11]虽考虑了无人机、任务的时序约束和时间约束，但研究对象是处于不同位置的任务，与对敌防空火力压制中每个目标需依次执行识别、打击和毁伤评估的作战任务存在较大区别。

1 问题描述

无人机编队对敌防空火力压制决策过程[1]如图1所示。一般由4架无人机组成1个作战编队，按预定模式在目标区域上空巡逻搜索，当发现敌潜在目标时，将各目标的识别、攻击和毁伤效果评估任务协同地分配给各架无人机，若为有效目标，则攻击之，并执行后续的评估任务；若目标不符合攻击准则，则放弃对该目标的攻击，并重新规划编队的作战任务；评估作战周期的效果，以确定是继续还是结束作战。

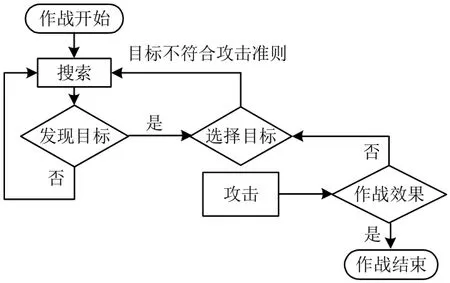
图1 对敌防空火力压制决策流程图Fig.1 Decision making flow chart of SEAD

为便于说明问题，作如下假设：①编队由具备自治能力的无人战斗机组成，具备发射兵器，侦察和识别潜在敌方目标，规避威胁的能力。②除非被敌方击落，编队成员数目不变，无人机攻击目标将导致所携带弹药的消耗，弹药耗尽后只能执行识别和评估任务。③将目标识别和攻击任务归为一个任务，每个目标必须依次执行ⓐ识别与攻击；ⓑ毁伤评估2项任务。通过合理的无人机—任务分派，使无人机任务执行代价、时间最小[3，8]或收益最大[7]，或者对上述多个目标的同时优化[9-10]，最终为每架无人机分配一条任务执行路线[6]是解决该问题的一般思路。

设经前期侦察发现地理上分散的n个目标，红方无人机数量为w，用n+w+1个节点来表示无人机执行任务的状态转换图，节点1,2,…,n位于发现目标的位置，节点n+1,n+2,…,n+w位于无人机的初始位置，入节点n+w+1为虚拟节点。若无人机没有分配任务，则进入入节点执行对区域内未知目标的搜索任务，不再参与当前的任务分配。

图2表示3架无人机与2个静止目标交战时的状态转换图。与文献[4]不同，本文状态转换图在目标结点上添加自环边以表示无人机攻击目标后折返再执行对该目标的毁伤评估任务。

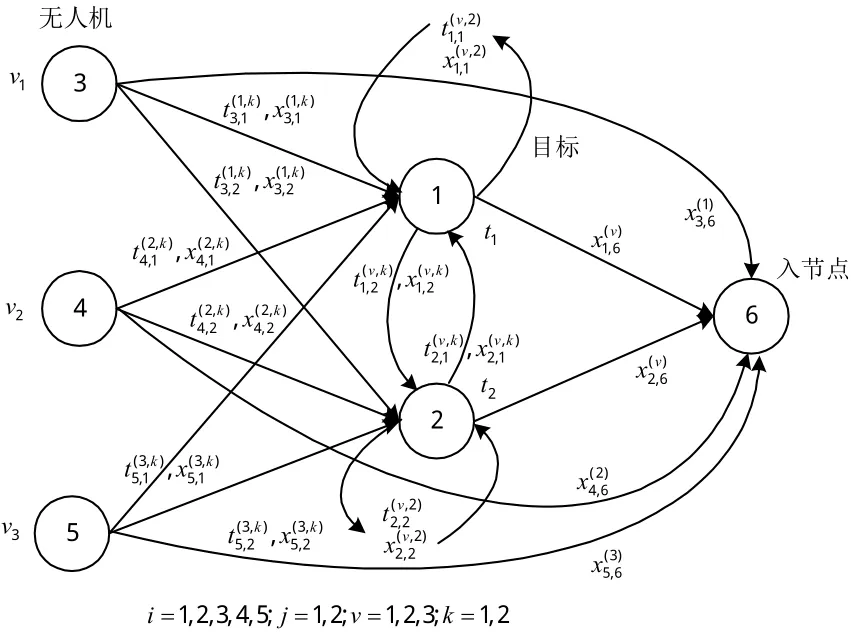
图2 2个目标3架无人机时的状态转换图Fig.2 State transition diagram for 2 targets 3 vehicles

2 MILP模型

MILP模型用状态转换图节点间的分段距离表示无人机的航路，以最小化交战时间为目标。

2.1 决策变量

2.1.1 0-1决策变量

如图1所示，若无人机v被指派从节点i飞向节点j执行任务k，则0-1决策变量，否则为0。其中，i=1,2,…,n+w，j=1,2,…,n，i≠j，v=1,2,…,w，k=1,2；若无人机被指派从节点i飞向入节点n+w+1，则决策变量，否则为0。其表明，该无人机被指派执行战场搜索任务而不参与当前目标任务的分配，其中，v=1,2,…,w，i=1,2,…,n+w。

2.1.2 连续时间决策变量

引入如下2类连续时间决策变量：①在目标j上执行任务k的时间为，k=1,2，j=1,2,…,n；②无人机v离开初始位置j=n+v的时间为tv，v=1,2,…,w。

2.2 目标函数

本文目标函数为最小化交战时间：

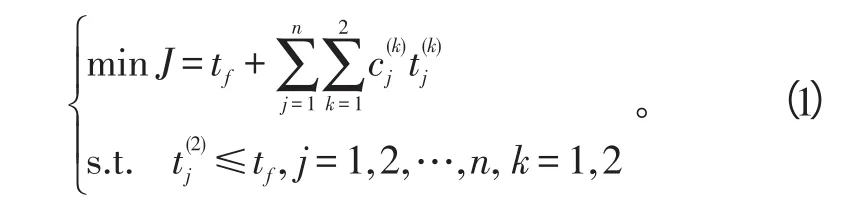
至此，求解本文多无人机多任务分配问题的决策变量如表1所示。0-1决策变量为2n2w+(2n+1)w个，连续决策变量为w+2n+1个。

2.3 非时间约束

为获得期望的无人机协同任务分配关系，应包括以下非时间约束。

1）每个目标的每项任务只能被执行1次：

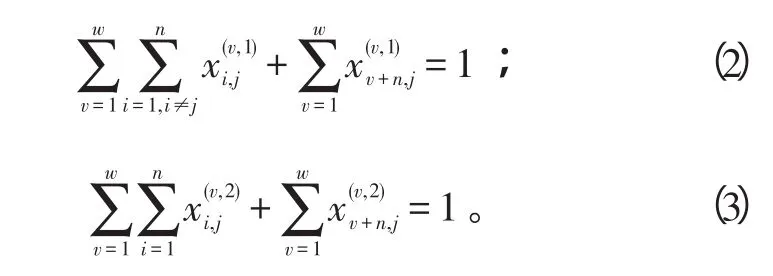
2）每个目标上要执行2项任务，1架无人机最多访问1个目标2次（依次执行任务1和2），

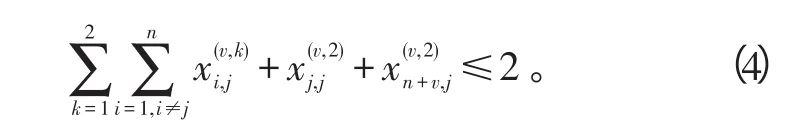
并且，每架无人机只能进入入节点1次，

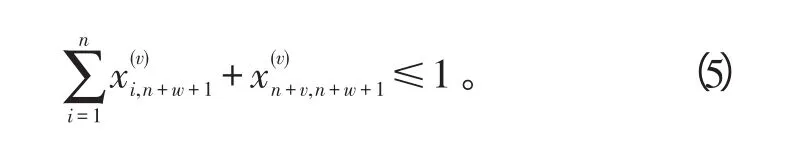
表1 决策变量Tab.1 Decision variables

3）一架无人机被指派执行攻击任务的次数不大于其携带的弹药数Mv，设Mv=3，

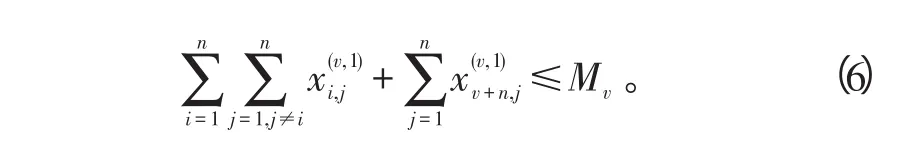
4）无人机不可能离开其未曾访问过的节点，

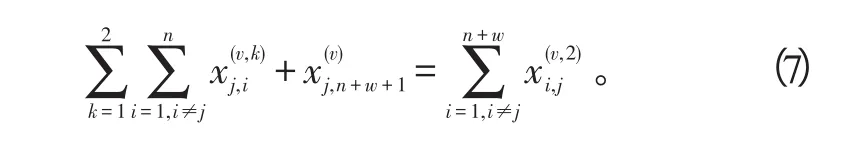
从状态转换图上可理解为，无人机v从其他节点进入节点j执行任务2的边数与该无人机由节点j飞向其他节点执行任意任务的边数之和相等，该约束不包括折返的自环边。

5）包括被指派去入节点执行区域搜索任务，所有无人机都离开源节点，

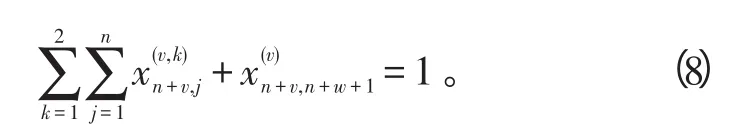
6）无人机只有进入某节点后才有可能选择自环边执行后续的评估任务，

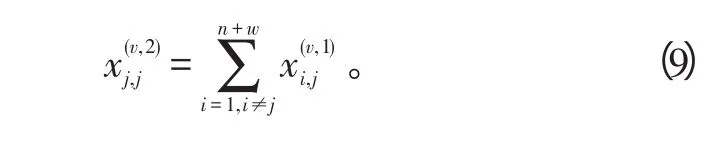
以上6个约束中，v=1,2,…,w，k=1,2。

2.4 时间约束

若无人机离开目标节点执行任务1，则线性化的时间约束可表示为：

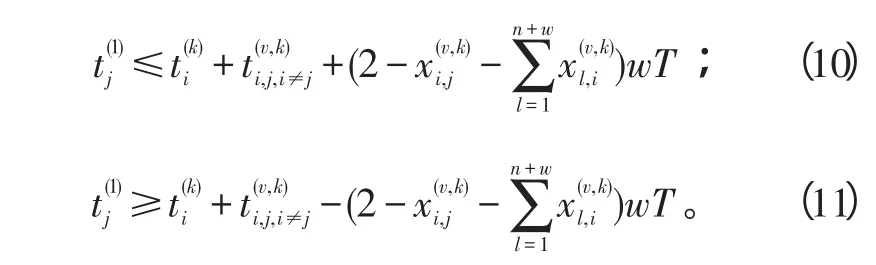
若无人机离开目标节点后折返执行任务2，则：

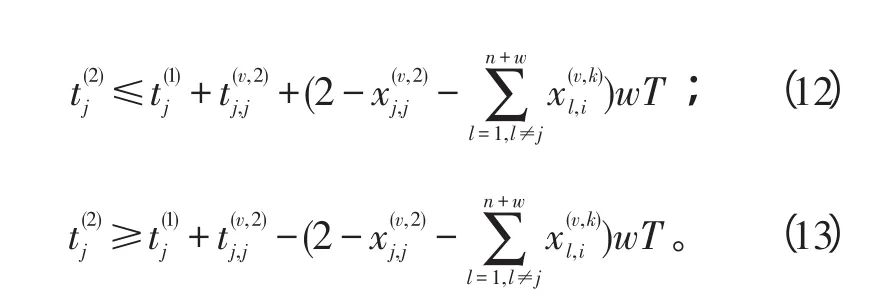
若无人机离开目标节点去其他目标节点执行任务2，则：

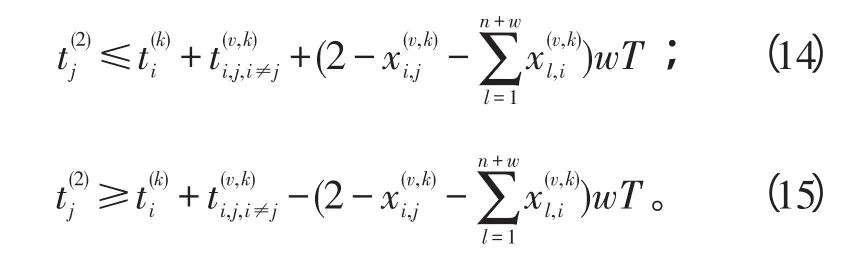
式（14）～（15）中：i=1,2,…,n；j=1,2,…,n，i≠j；v=1,2,…,w；k=1,2。

以上约束影响由其他目标节点飞来执行任务的无人机所需时间。

时间约束还包括：

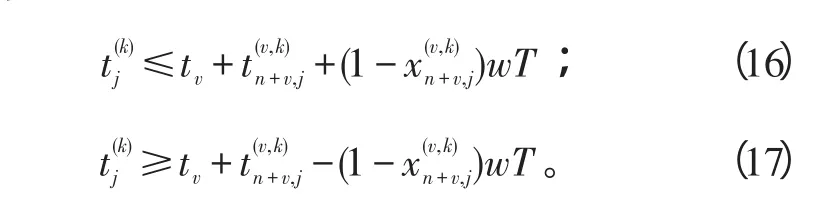
式（16）～（17）中，j=1,2,…,n；k=1,2；v=1,2,…,w。

此类约束影响每架无人机从源节点出发执行的首个任务。

考虑任务1与2之间的时间延迟，引入约束：

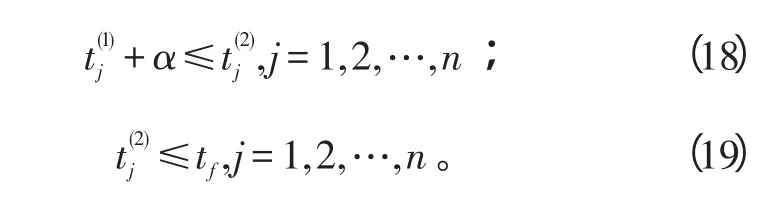
其中，α为任务1的最小处理时间。

由分析可知，非时间约束数为3nw+3w+2n，时间约束为6nw+8n(n-1)w+2n。

3 算例分析

设下述例子初始条件用无人机及目标节点间的相对飞行时间表示，且无人机由节点i飞向节点j执行任务k的时间与无人机及任务无关，则常量可用ti,j表示，所有无人机的最大飞行时间均为100。用矩阵T表示相对飞行时间[4]，列表示开始节点i，行表示终节点j，对角线元素表示无人机在执行完任务1后折返执行任务2的最小时间。

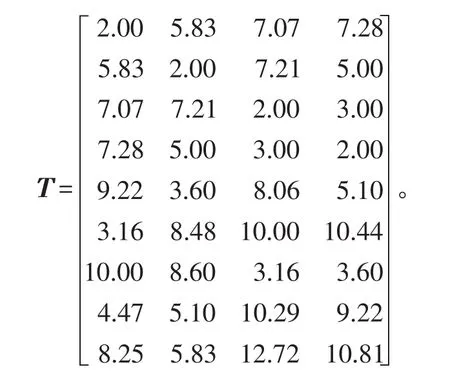
3.1 2架无人机1个目标

该场景下，n=1，w=2，0-1决策变量数为10，连续时间决策变量数为4，为最小化交战时间，引入附加连续决策变量tf，共计15个决策变量。

0-1决策变量为：

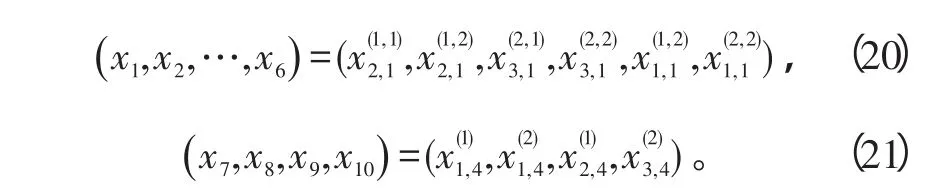
连续决策变量

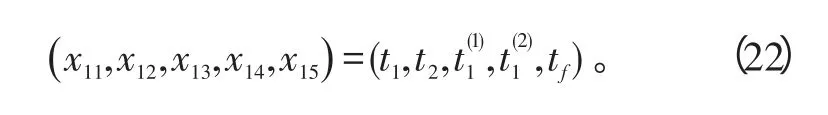
目标函数

由约束1得：x1+x3=1，x2+x4+x5+x6=1；

由约束2得：x7+x9≤1，x8+x10≤1，x5+x2≤2，x6+x4≤2；

由约束3得：x1≤3，x3≤3；

由约束4得：x9=x2，x10=x4；

由约束5得：x1+x2+x7=1，x3+x4+x8=1；

由约束6得：x5=x1，x6=x3；

此处只有1个目标节点，因而等式（10）、（11）和（14）、（15）没有意义。

由等式（12）、（13）和（16）、（17）得到的时间约束为：

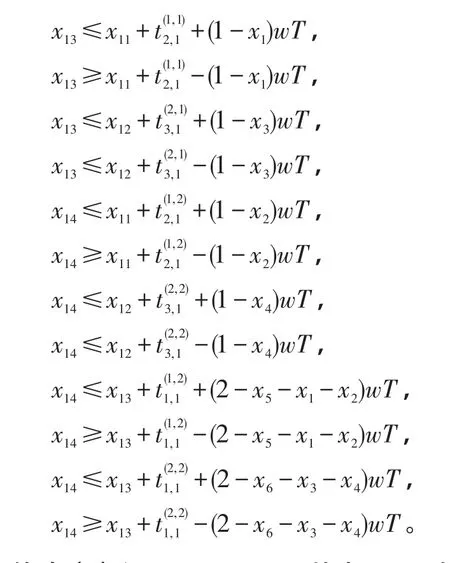
由等式（18）得：x13≤x14-α，其中α〉0为一小的正常量，本文设α=0.1，表示目标前导任务的处理时间。

最后，由等式（19）得：x14≤x15。

用软件CPLEX求解上述混合整数规划问题得：xi=1,i=1,4,6，xi=0,i=2,3,5,7,8，xi=0,i=9,10，x11=5.83，x12=7.07，x13=7.07。这表示，无人机1，2立即离开源节点，无人机1在t=5.83时刻执行对目标的识别和攻击任务，无人机2在t=7.07时刻执行对目标的毁伤评估任务。若无人机执行任务1耗时α=2.0，则有x10=0.76，x12=7.83，此时无人机2要等待0.76才从源节点出发来完成对目标任务2的处理。

3.2 多目标多无人机场景

该算例为用如图3所示的节点图表示的4个目标5架无人机的最优任务分配结果。

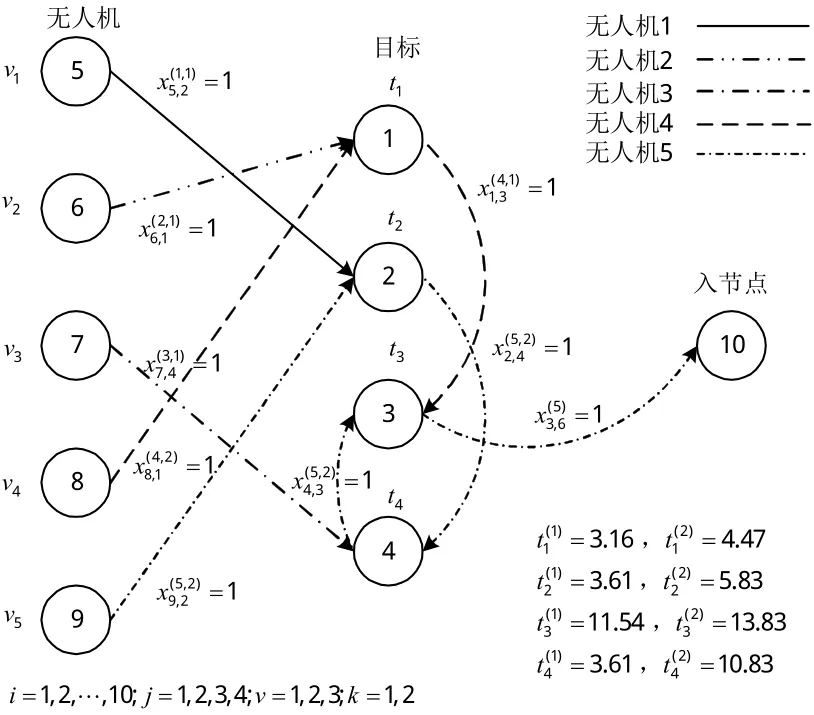
图3 4个目标5架无人机时的最优任务分配Fig.3 Optimal assignment for 4 targets 5 vehicles

表2为不同问题规模时，利用CPLEX求解模型的运行时间。

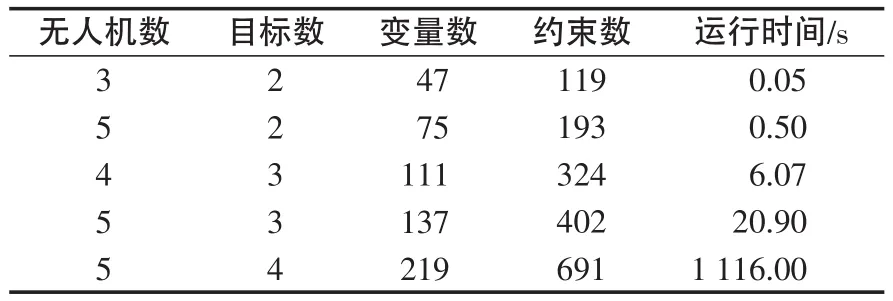
表2 问题规模与求解时间Tab.2 Scale of the problem and solution time

由表2可知，当由4架无人机组成的编队在处理不超过3个目标时，运用该模型可得到实时的最优分配结果，而对更大规模的问题可按分层分级的方法来分解求解。

4 结论

建立了耦合时序约束和时间约束的多无人机多任务分配问题的混合整数线性规划模型，引入连续时间决策变量，以描述任务执行时间和无人机离开源位置时间以满足时间约束。该模型还可提供多种目标函数表达式，以满足不同的任务完成评价指标。仿真实验表明，对符合实战的问题规模，利用商用软件可得到实时的可行优化解。

[1] CANDIR A A.Discrete event simulation of a suppression of enemy air defenses（SEAD）mission[D].Ohio：Air Force Institute of Technology，2008.

[2] SURANZYNSKI.Miniaturized unmanned aerial systems（UAS）in SEAD m issions during electromagnetic conflicts[R].London：International Quality and Productivity Center，2006：912-913.

[3] 张雷，孙振江，王道波，等.一种用于SEAD任务的改进型Voronoi图[J].国防科技大学学报，2010，32（3）：121-125. ZHANG LEI，SUN ZHENGJIANG，WANG DAOBO，et al.An improved voronoi diagram for suppression of enemy air defense[J].Journal of National University of Defense Technology，2010，32（3）：121-125.（in Chinese）

[4] SCHUMACHER C，CHANDLER，P R.Optimization of air vehicle operations using m ixed-integer linear programm ing，0704-0188[R].W right Patterson：Air Force Research Laboratory，2006.

[5] SHIMA T，RASMUSSEN S J.Multiple task assignments for cooperating uninhabited aerial vehicles using genetic algorithms[J].Computers&Operations Research，2006，33：3252-3269.

[6] 杨尚君，王社伟，陶军，等.动态环境下的多UCAV协同任务分配研究[J].电光与控制，2012，19（7）：32-36. YANG SHANGJUN，WANG SHEWEI，TAO JUN，et al. Multi-UCAV cooperative task allocation in dynam ic environment[J].Electronics Optics＆Control，2012，19（7）：32-36.（in Chinese）

[7] 邸斌，周锐，丁全心.多无人机分布式协同异构任务分配[J].控制与决策，2013，28（2）：274-278. DI BIN，ZHOU RUI，DING QUANXIN.Distributed coordinated heterogeneous task allocation for unmanned aerial vehicles[J].Control and Decision，2013，28（2）：274-278.（in Chinese）

[8] 龙涛，沈林成，朱华勇，等.面向协同任务的多UCAV分布式任务分配与协调技术[J].自动化学报，2007，33（7）：731-737. LONG TAO，SHEN LINCHENG，ZHU HUAYONG，et al.Distributed task allocation&coordination technique of multiple UCAV for cooperative tasks[J].Acta Automatica Sinica，2007，33（7）：731-737.（in Chinese）

[9] 宋磊，黄长强，吴文超，等.多UCAV协同目标攻击决策[J].系统工程与电子技术，2011，33（7）：1548-1552. SONG LEI，HUANG CHANGQIANG，WU WENCHAO，et al.Target attack decision-making for cooperating multi-UCAV[J].Systems Engineering and Electronic，2011，33（7）：1548-1552.（in Chinese）

[10] 程聪，吴庆宪，刘敏，等.UCAV协同攻击多目标的任务分配技术研究[J].吉林大学学报：信息科学版，2012，30（6）：609-615. CHENG CONG，WU QINGXIAN，LIU MIN，et al.Research on task allocation for ucavs cooperatively attacking multiple targets[J].Journal of Jilin University：Information Science Edition，2012，30（6）：609-615.（in Chinese）

[11] 张健，彭志红，李波.考虑时间代价及硬时间窗的UCAVs多任务分配[C]//中国控制学会第31届学术会议.华盛顿：IEEE计算机学会，2012：2448-2452. ZHANG JIAN，PENG ZHIHONG，LI BO.Multi-task allocation of UCAVs considering time cost and hard time w indow constraints[C]//Proceedings of the 31st Chinese Control Conference.Washing，D.C.：IEEE Computer Society，2012：2448-2452.（in Chinese）

Multi UAV Suppression of on Enemy Air Defense Based on MILP

YAN Ji1a,LI Xiang-min1b,LIU Bo2,LIU Li-jia1a
（1.Naval Aeronautical and Astronautical University a.Graduate Students'Brigade; b.Department of Ordnance Science and Technology,Yantai Shandong 264001,China; 2.Science and Technology on Electro-Optic Control Laboratory,Luoyang Henan 471009,China）

A problem of assigning cooperating uninhabited aerial vehicles to perform multiple tasks on multiple targets in a suppression of enemy air defense(SEAD)mission was proposed as a mixed integer linear program(MILP).Additions to the binary task assignment decision variable,a serial of continuous decision variables were introduced to represent the task precedence.The equality and inequality non-timing and timing constraints of decision variables take into account the unique requirements of UAVs and tasks were constructed.The problem was solved by CPLEX,and simulations demonstrated the viability of the model.

suppression of enemy air defenses;task allocation;mixed integer linear program(MILP);cooperating multi air vehicle

V279

A

1673-1522（2014）04-0369-05

10.7682/j.issn.1673-1522.2014.04.015

2014-03-03；

2014-04-28

航空科学基金资助项目（20135184008）

颜骥（1984-），男，博士生。