基于动态时差和粒子群算法的导弹技术保障人力资源优化配置方法
基于动态时差和粒子群算法的导弹技术保障人力资源优化配置方法
针对导弹技术保障中人力资源使用大起大落现象,将粒子群算法运用到网络计划的资源均衡优化中。研究了资源均衡优化问题的评价模型,引入了基于动态时差的优化方法,提出了基于粒子群算法的资源均衡优化方法,选取了一个算例进行了实例验算,验证了该方法在导弹技术保障人力资源优化配置中的可行性和有效性。
导弹技术保障;人力资源;优化配置;粒子群算法
项目管理是现代管理学中的一项重要内容。它是通过项目经理和项目组织的努力,运用系统的理论和方法对项目及其资源进行计划、组织、协调和控制,旨在建立特定目标的管理方法体系[1-2]。项目管理的工具主要是网络计划技术及优化方法。网络计划图绘制出来之后,通常需要再进行工期优化和资源优化。本文将项目管理的思想引入导弹技术保障人力资源优化配置中,针对资源优化展开重点研究。网络计划技术中工期固定资源均衡优化的传统方法可分为最优化方法和直接推理方法。求解组合优化问题,若不能利用问题固有的知识来缩小搜索空间则会产生搜索的组合爆炸。因此,研究能在搜索过程中自动获取和积累有关搜索空间的知识,并自适应地控制搜索过程,从而得到最优解或准最优解的通用搜索算法一直是令人瞩目的课题。本文尝试将粒子群优化算法应用于导弹技术保障人力资源优化配置。
1 导弹技术保障人力资源优化配置模型
1.1 导弹技术保障网络计划图的绘制
网络计划技术的基础是网络分析法,它以时间为基础,把工程计划和工程控制过程作为一个整体表述出来,使人们可以直观地了解到各分系统的内在联系,增强了工作的条理性,其工具就是网络计划图。网络计划图是通过节点N和箭线A的集合表示的,即G(N,A)。它将工作、事件和线路有机地构成一个整体,有效地反映了整个任务的全貌。编制网络计划一般包括资料汇编、任务分解、工作明细表编制、网络图绘制4个步骤。Project、PERT等软件都提供双代号网络图绘制功能。这类软件界面简洁,操作方便,并可以自动计算时差和寻找关键线路,是理想的网络图绘制工具[3-4]。绘制出网络计划图后,可以清晰地表达项目中各项任务之间的进度和它们之间的相互关系,并在此基础上进行网络计划的分析和优化。
1.2 导弹技术保障人力资源优化配置问题的提出
理想的导弹技术保障资源安排是保持每个时段保障资源需求量不变。但由于操作过程的不均衡性,单位时间内对保障资源的需求量常会出现高峰和低谷的现象。导弹技术保障项目工序较多,如项目计划安排不合理,就会出现人力资源使用量的大起大落现象。在资源使用高峰期,会出现某些时段的最大人力资源需求量超过该时段人力资源的限量,导致工作无法正常进行,同时也增加了保障系统的负荷,影响保障质量;在资源使用低谷期,就会出现人力资源未得到充分利用等问题,从而影响技术保障的协调管理。
因此,在任务工期规定下,合理地调整网络计划中的某些工作使得资源均衡使用,从而减少人力资源在使用过程中需求量的起伏,降低调度管理难度以及提高资源的利用率,这就是“工期固定资源均衡”优化问题,简称为资源均衡优化问题。
1.3 导弹技术保障人力资源优化配置模型的建立
评判资源均衡程度的指标一般有3种。
1)不均匀系数:

式中,Qmax、Qm分别表示单位时间内资源需要量的最大值和平均值[5]。可见,不均匀系数K越小,资源需要量的均衡性就越好。
2)极差:

式中,Qi表示第i个时间段的资源需要量。可见,极差ΔQ越小,资源需要量的均衡性越好。
3)均方差:
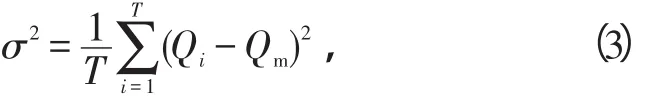
式中,T为网络计划的工期。可见,均方差σ2越小,资源需要量的均衡性越好。
本文采用均方差σ2的指标来评判资源需要量的均衡性,即用单位时间资源消耗量距水平线y=Qm的离散程度来衡量一个调度方案的优劣。最理想的情况就是资源动态曲线趋近于矩形分布,即以Qm为高,规定工期T为长度的矩形。资源均衡优化的模型:

式(4)~(8)中:T为任务总工期,为固定值;R(t)为第t个时间单位所有工作的资源消耗量之和;Rm为当前网络计划资源强度分布的平均值;Ri,j(t)为工作(i,j)在时刻t的资源强度;tES(i,j)为工作(i,j)的最早开工时间;tLS(i,j)为工作(i,j)的最迟开工时间;tA(i,j)为工作(i,j)的实际开工时间;d(i,j)为工作(i,j)的持续时间;F(i,j)为工作(i,j)所有紧前工作的集合。
资源均衡问题的实质,就是利用总时差和自由时差来重新安排各项工作的开工时间,错开资源利用的高峰期和低谷期,使资源需要量的均方差最小化[6]。因此,该模型的实质是寻求任务中所有工作实际开工时间的最优组合,从而使目标函数达到最小。
2 模型的优化求解
2.1 优化过程分析
从人力资源均衡的数学模型中可以看到,活动受到逻辑关系约束和时间关系约束,活动的实际开始时间不仅被限定在最早开始时间和最晚开始时间范围内,而且还受到该活动所有紧前活动状态的影响,使得可用总时差受到一定的限制[7]。
本文综合考虑了工程网络计划资源均衡优化问题中高度隐匿约束的特点,提出了基于动态时差的资源均衡优化方法:把这种逻辑约束关系直接加入到活动的时差范围确定当中,认为活动在受逻辑关系约束和时间关系约束时,活动的总时差并不是固定在某个范围内的,而是随着工程进行过程中紧前活动的实际开始时间的确定,动态地发生变化。基于这个思想,在运用粒子群算法求解时,对粒子群初始化阶段和进化后处理过程,将算法做出相应的改进,使得计算过程中避免了非可行解的产生。具体改进方法如下:
1)当没有紧前活动时,tA(i,j)∈[] tES(i,j),tLS(i,j);
这样,后续活动的实际开始时间必须在紧前活动的实际开始时间确定以后才能够确定,每个活动可利用的总时差范围总是在变动的。既保证活动同时满足逻辑关系约束条件和时间关系约束条件,又避免了产生非可行解,保证了结果的合理性。
根据资源均衡优化原理,可以把目标问题的可行解空间假想为粒子的N维搜索空间,N代表该问题中的活动数目。目标问题的所有可行解如同散布在空间中的离散点,粒子在某时刻所处的位置Xi=(xi1,xi2,…,xiN)对应问题的一个可行解,其中xij(i=1,2,…,M,j=1,2,…,N)的值表示粒子i所对应的方案中第j个活动的实际开始时间,也就是说粒子和方案相对应,而粒子的每一维的坐标和方案中每个活动的实际开始时间所对应:M表示初始粒子群中的粒子数;[xj,min,xj,max]表示粒子在第j维空间上的活动范围,其中xj,min表示活动j的最早开始时间,xj,max表示活动j的最晚开始时间。粒子通过不断地进化,不断地改变位置,逐渐到达处于最佳适应度值的位置,即活动的最佳安排方案[8-9]。
考虑到活动总时差是动态的,因而在进行粒子群初始化时,就不能按原来算法那样在[xj,min,xj,max]上随机产生了,必须做出调整。要判断每个粒子的某一维对应的活动是否有紧前活动,找出该活动的所有紧前活动中,实际完成时间最大的粒子的空间坐标[10-11]。
由于粒子种群位置是不固定的,每个粒子的空间坐标也在不停地变化,这种变化使得粒子可能在可行空间内,也有可能跳出可行空间,变成非可行解。因此,在每次进化后,还要对基本粒子群算法做出改进,使得粒子在每次移动后,能始终在可行解空间内。即判断每个粒子的某一维对应的活动是否有紧前活动,找出该活动所有紧前活动中,实际完成时间最大值。
通过对粒子群初始化过程和粒子群进化后处理,保证了每个粒子的位置总是在可行解空间中,产生的解也总是满足目标问题的,避免了非可行解的产生。
2.2 资源优化配置的粒子群算法设计
1)粒子个体的结构与编码。资源配置问题是在时序约束下利用自由时差调整各项工作的开工时间,从而得到多种不同的调度方案,并在众多方案中寻找资源均方差最小者的过程。调整工作的自由时差就是延迟工作的开工时间,因而粒子个体可这样设计:一个粒子对应一组工作序列,粒子的值代表该工作序列内部各个工作的开工时间。
2)开工时间范围计算。模型约束条件(7)表明,时差的存在使工作的开工时间可以在一定范围内浮动。由于在求解模型的过程中,网络计划在不断进行调整,工作的开工时间范围也在不断变化,所以要确定某项工作的开工时间,就必须求出该工作的开工时间范围。
图1为在工作的开工时间确定后,计算其紧前工作的开工时间范围的流程图。
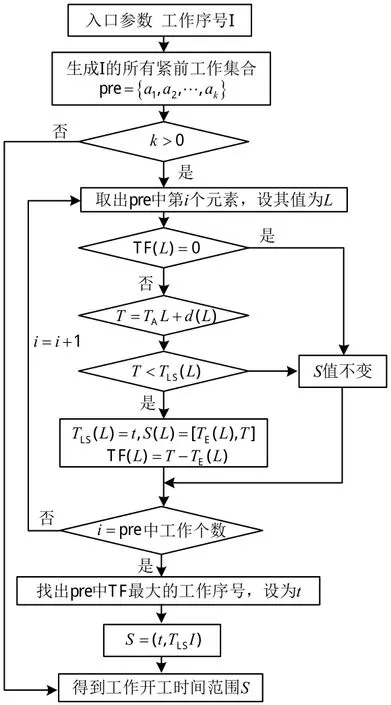
图1 开工时间范围流程图Fig.1 Flow chart of start time span
3)初始种群生成。一个工作开工时间的确定会影响其他工作开工时间范围,所以在生成不同粒子群组成初始种群时,若按照粒子群本身对应的工作顺序依次为各工作在其对应时间范围确定开工时间,将导致优先级固定,从而使顺序靠后的工作得到相同总时差的概率大为减少,使种群缺乏多样性[12]。本文在生成每个粒子群前,先随机生成一个非关键工作排序,再依次从对应时间范围随机确定其开工时间,每得到一个工作的开工时间后,再重新确定其他工作的开工时间范围。这样,每个工作的优先级理论上相同,保证种群具有广泛的多样性。其流程见图2。这样,一个粒子群就对应模型(4)的一个可行解,一定数量粒子群组成的初始种群就对应模型解空间的一个子集。
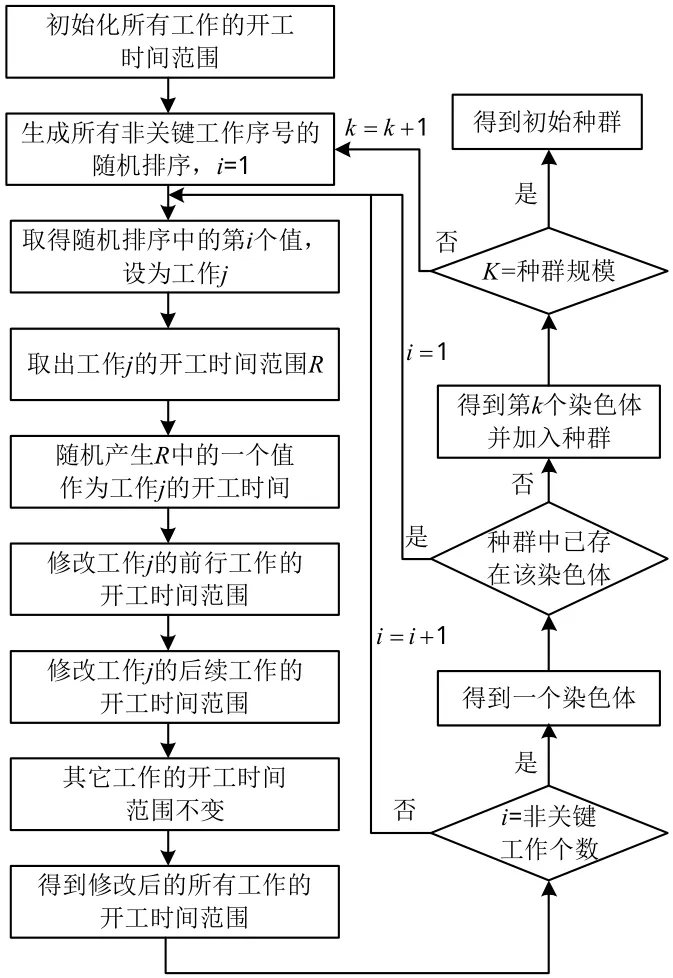
图2 初始种群生成流程图Fig.2 Flow chart of creating the initial population
4)评价函数。评价函数的规则使资源使用量均方差越小的个体适应度值越大,随着粒子群的进化,算法最终找到方差最小的资源计划。由于模型(4)是寻求目标函数的最小化,要将原始目标函数转换为适应度值函数,以确保适合的个体具有大的适应度值。这可由下述转换过程实现:

式(9)中:x表示当代种群的某个粒子;f(x)表示粒子x的适应度;表示当代目标函数即资源使用量均方差的最大值与最小值;σ2(x)表示粒子x对应的资源使用量的均方差。
5)收敛条件。收敛性是粒子群算法的一个重要问题,它可以说明这种算法找到的可行解是否是最优的或者当前找到的解是否满足精度要求。Fans van den Bergh给出了一种粒子群优化算法的收敛定义[13]。
定义1:设粒子群中某粒子在t时刻位置为x(t),P为整个搜索空间内的某任意位置,则粒子收敛:

该定义表明粒子群算法的收敛是指群中的某个粒子最终停留在搜索空间的某一个固定位置。在分析了粒子的运行轨迹后,Fans van den Bergh还指出,对于粒子群中的所有粒子来说,他们都将最终收敛到全局最优粒子所在的位置。
通过Fans van den Bergh的定义可知,粒子群的历史最佳适应度值gBest是迭代信息t的一个函数,随t的变化,gBest(t)不断地变化,且当t→∞时,gBest(t)趋向于一个固定的值,即

通常,算法的寻优过程就是不断保留历史最佳适应度值的过程,理论上已证明了算法可全局收敛,但现行的计算能力和条件下需要花费相当长的时间,这也是目前各种智能仿生类算法急需解决的问题之一。实际运用中,通常采取另外一种策略,即保存当前最优个体值。这样,在规定的进化代数下,都能够以概率1找到全局最优解,这也是目前众多智能仿生算法所采用的近似收敛策略。具体做法是在程序运行前,设置一个最大进化代数G,使得程序运行G代后自动终止,把当前找到的最优解作为全局最优解。
6)算法流程。PSO的流程如图3所示[14],其中pBest为个体极值。
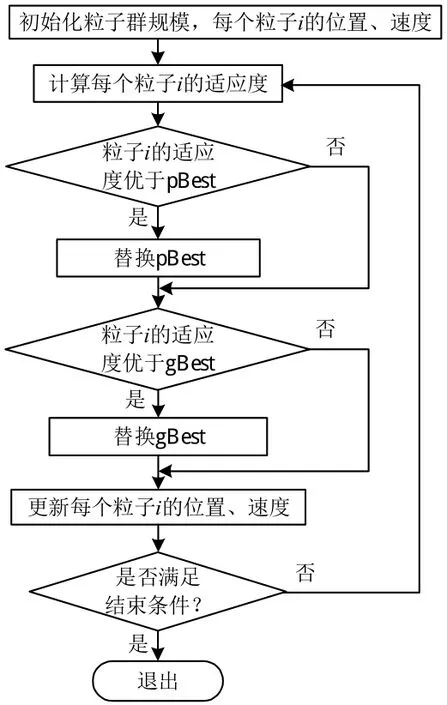
图3 算法流程图Fig.3 Flow chart of PSO
3 案例分析
假设一项导弹技术保障任务由9项工作组成,工序参数见表1。任务的网络计划图及资源分布直方图如图4所示,总工期为14 d,关键线路为:A-D-G-I。由图可见,人力资源分布非常不均。最高值达20人/d,而最低值仅为5人/d,均方差为24.41,起伏非常大。因此,有必要对该任务进行资源配置优化。
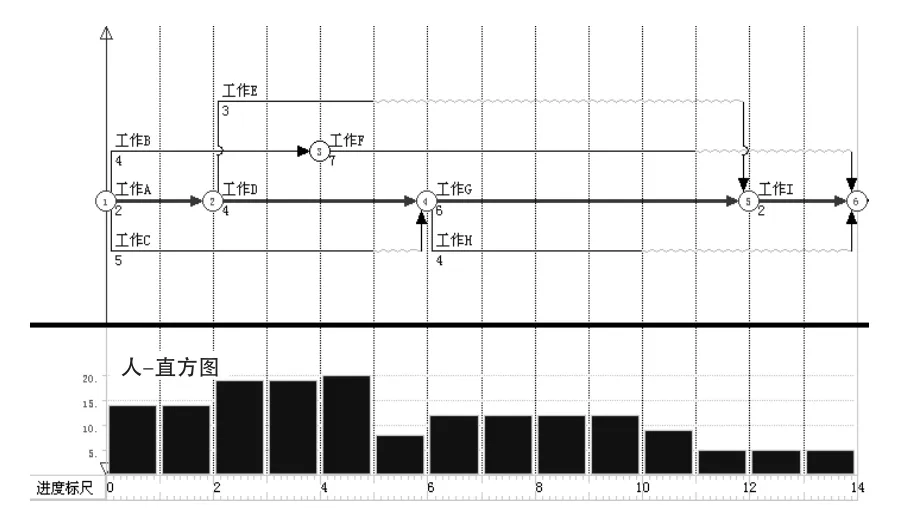
图4 优化前网络图和资源直方图Fig.4 Network graph and bin graph of resource before optimization
依照开工时间流程图的设计,对该任务中各个工作的开工时间进行计算,得到如表1所示的工序参数表。其中,最早/迟开工时间在1~14之间,因为总工期为14 d。

表1 工序参数表Tab.1 Parameters of activities
使用Project 2003对算例进行资源均衡优化,得到的优化方案资源直方图如图5所示,优化后的均方差为10.70。

图5 Project优化方案资源直方图Fig.5 Bin graph of resource of scheme optim ized by Project
采用本文提出的粒子群算法对算例进行优化,粒子群算法的参数设置为:粒子群初始种群取20个,粒子个体长度依据任务需求取9,其中每一个代表A~I工作的开工时间;粒子中各项工作的最早和最迟开工时间如表1所示;加速常数c1、c2分别取1.2和0.8;惯性权重系数ω取0.9;进化代数为100代。
优化后的网络图和资源直方图如图6所示,开工时间表如表2所示,粒子群算法的每代最小资源使用量均方差变化如图7所示,可见随着进化代数的增加,群体的最小均方差在不断减小,最后趋于平稳,优化后的均方差为2.84,3种方案的相关指标对比如表3所示。

图6 粒子群算法优化后网络图和资源直方图Fig.6 Network graph and bin graph of resource of scheme optim ized by PSO
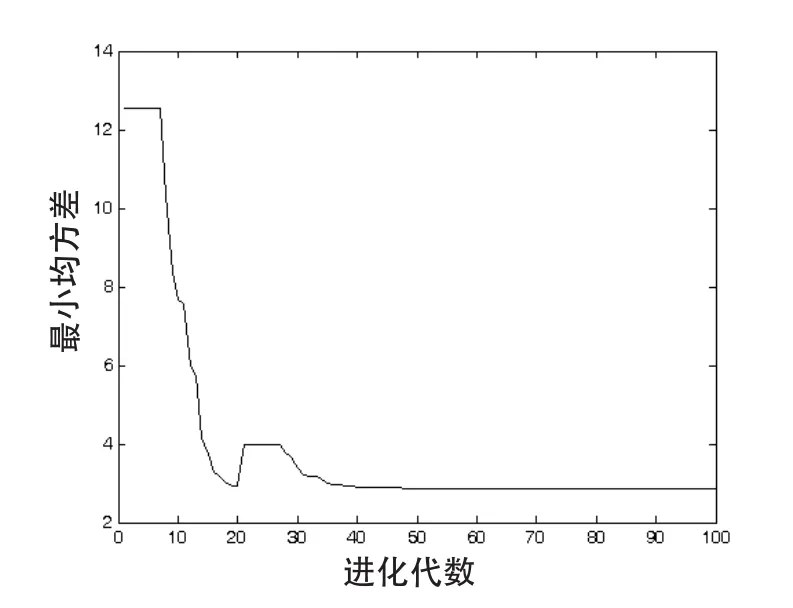
图7 每代最小资源量均方差Fig.7 Minimum mean covariance of resource amount of each generation

表2 PSO优化后工作开工时间表Tab.2 Start time of each activity after optimization by PSO
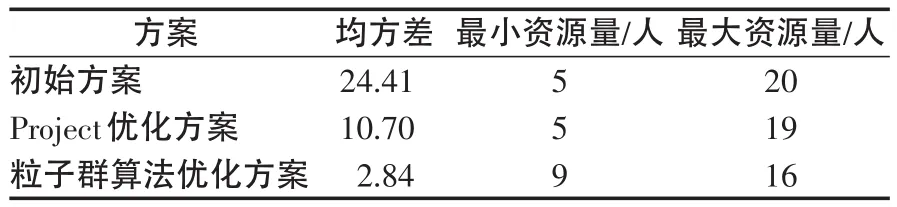
表3 3种方案结果对比Tab.3 Results contrast of 3 schemes
可见,在Project优化方案中,资源需要量均方差为10.70,比初始方案减少了56.2%。本文粒子群算法优化方案中,资源需要量均方差为2.84,比初始方案减少了88.4%,比Project优化方案减少了73.4%,同时资源使用量的范围也大大缩小,避免了资源使用的大起大落现象。显然,本文的方法具有更好的优化效果。
4 结束语
为了提高导弹保障资源利用效率,本文研究了导弹技术保障人力资源优化配置方法。分析了目前关于资源均衡优化问题的评价模型,引入了基于动态时差的优化方法,提出了基于粒子群算法的资源均衡优化方法;并对某型导弹技术准备流程的人力资源进行优化,取得了较满意的结果,从而验证了基于动态时差思想和粒子群算法的导弹保障资源优化配置方法的可行性和有效性。
[1] 胡长明,刘凯,董翔,等.多项目管理组织结构及其评价[J].广西大学学报:自然科学版,2014,39(1):206-213. HU CHANGMING,LIU KAI,DONG XIANG,et al. Structure and evaluation of multi-project management[J]. Journal of Guangxi University:Natural Science Edition,2014,39(1):206-213.(in Chinese)
[2] 唐孜聪.浅析成功的项目管理的影响因素[J].江苏科技信息,2014(5):44-45. TANG ZICONG.Structure and evaluation of multi-project management[J].Jiangsu Science&Technology Information,2014(5):44-45.(in Chinese)
[3] 江景波,葛震明,何治.网络技术原理及应用[M].上海:同济大学出版社,1997:23-36. JIANG JINGBO,GE ZHENMING,HE ZHI.Network technology theory and application[M].Shanghai:Tongji University Press,1997:23-36.(in Chinese)
[4] JOHN B K.A comparison between the VERT program and other methods of project duration estimation[J].Management Science,1987,15(2):129-134.
[5] 刘建,李松涛.时标网络资源均衡优化方法研究[J].西华大学学报:自然科学版,2011,30(4):8-10. LIU JIAN,LI SONGTAO.Research of resources leveling optimization based on time-scaled network diagram[J]. Journal of Xihua University:Natural Science,2011,30(4):8-10.(in Chinese)
[6] 公茂果,焦李成,杨咚咚.进化多目标优化算法研究[J].软件学报,2009,20(2):271-289. GONG MAOGUO,JIAO LICHENG,YANG DONGDONG.Research on evolutionary multi-objective optim ization algorithms[J].Journal of Software,2009,20(2):271-289.(in Chinese)
[7] EBERHART RC,SHI YAN.Tracking an optim izing dynamic systems with particle swarm[C]//IEEE Congress on Evolutionary Computation.2001:94-100.
[8] HU XIANG,EBERHART.Multi-objective optim ization using dynamic neighborhood particle swarm optim ization [C]//IEEE Proceedings of the 2002 Congress on Evolutionary Computation.2002:185-190.
[9] MOSTAGHIMS,TEICH J.Strategies for finding good local guides in multi-objective particle swarm optim ization[C]//IEEE Swarm Intelligence Symposium.2003:26-33.
[10] COELLO M,PULIDO C,LECHUNGA G.Handling multiple objectives with particle swarm optim ization[C]// IEEE Transactions on Evolutionary Computation.2004:256-279.
[11] CLERE MAND KENNEDY J.THE.Particle swarm:explosion,stability and convergence in a multi-dimensional complex space[C]//IEEE Transactions on Evolution Computation.2002:68-73.
[12] 潘全科,王凌,高亮.离散微粒群优化算法的研究进展[J].控制与决策,2009,24(10):1441-1449. PAN QUANKE,WANG LING,GAO LIANG.The research development of discrete particle swarm optimization algorithm[J].Control and Decision,2009,24(10):1441-1449.(in Chinese)
[13] 杨虎,许峰.基于聚集密度的粒子群多目标优化算法[J].计算机工程与应用,2013,49(17):190-194. YANG HU,XU FENG.Multi-objective particle swarm optimization algorithm based on crowding-density[J]. Computer Engineering and Applications,2013,49(17):190-194.(in Chinese)
[14] TRELEA I C.The particle swarm optimization algorithm:convergence analysis and parameter selction[J].Information Processing Letters,2003,85(6):317-325.
刘纪文1,张磊2a,赵建忠2b
(1.海军装备部,北京100036;2.海军航空工程学院a.科研部;b.兵器科学与技术系,山东烟台264001)
Optimal Configuration Method of Missile Technical Support Human Resources Based on Dynamic Time-Delay and PSO
LIU Ji-wen1,ZHANG Lei2a,ZHAO Jian-zhong2b
(1.Naval Equipment Department,Beijing 100036,China;2.Naval Aeronautical and Astronautical University a.Department of Scientific Research; b.Department of Ordnance Science and Technology,Yantai Shandong 264001,China)
Aiming at the disequilibrium phenomenon of manpower resource in missile technical support,in this paper,the particle swarm optimization(PSO)was brought to resource leveling optimization of network plan.The current evaluation model of resource leveling optimization was analyzed,the optimization method based on dynamic time-delay was introduced,and the resource leveling optimization method based on PSO was brought forward.Through the analysis to the calculation result,the feasibility and validity of the method was validated in optimal configuration of missile technical support manpower resource.
missile technical support;human resources;optimal configuration;particle swarm optimization(PSO)
TP391.9
A
1673-1522(2014)04-0385-06
10.7682/j.issn.1673-1522.2014.04.018
2014-03-28;
2014-05-14
刘纪文(1967-),女,高工,硕士。

