一类Cohen-Grossberg型神经网络概周期解的全局指数稳定
张强,盖明久,张宁,崔世维
(海军航空工程学院a.基础部;b.训练部;c.研究生管理大队,山东烟台264001)
一类Cohen-Grossberg型神经网络概周期解的全局指数稳定
张强a,盖明久a,张宁b,崔世维c
(海军航空工程学院a.基础部;b.训练部;c.研究生管理大队,山东烟台264001)
研究了一类Cohen-Grossberg型神经网络概周期解的存在唯一性及全局指数稳定性,得到了判断概周期解存在唯一及全局指数稳定的充分条件,推广了一些已有的结论。
Cohen-Grossberg型神经网络;概周期解;稳定性
与周期现象相比,概周期现象是一种更普遍的现象。事实上,从物理实现方面看,神经网络是由超大规模集成电路实现的,它拥有大量的神经元,且每个神经元都有自己的信号衰减系数、与其他神经元的连接权系数以及外部输入,因而很难做到它们都具有相同的周期。同时,由于神经网络电路的外部输入是由市电供应的,而电力系统本身就存在概周期现象,这样就使得神经网络的信号衰减系数、连接权系数以及外部输入可能具有概周期振荡行为。因此,研究神经网络的性质时就有必要研究这种概周期振荡现象。
关于Hopfield神经网络、细胞神经网络、BAM神经网络概周期解的存在性及稳定性,许多学者进行了深入的研究[1-9]。同时,由于Cohen-Grossberg神经网络在模式识别、图像处理等方面的成功运用,关于这类网络的概周期解的研究引起了国内外学者的广泛关注,并取得了一些很好的研究成果[10-12]。在文献[13]中,Chen研究了Cohen-Grossberg神经网络

概周期解的存在性及全局指数稳定性。本文将系统中的常时滞推广为变时滞,并同时考虑分布时滞存在的情况下,研究如下一类Cohen-Grossberg神经网络概周期解的存在性及全局指数稳定性:
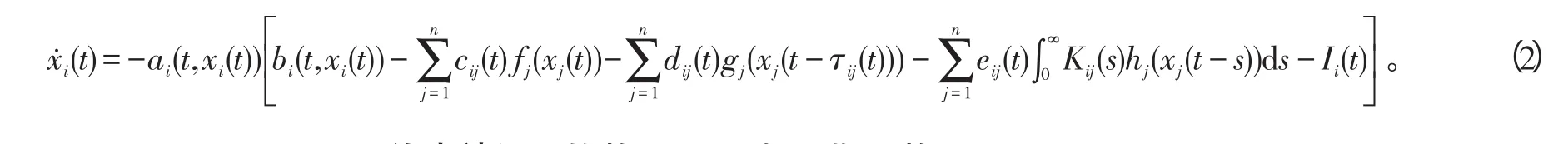
式(2)中:i=1,2,…,n,n≥2是网络中神经元的数量;xi(t)表示第i个神经元在t时刻的状态;fj(·)、gj(·)、hj(·)是激励函数;0〈τij(t)〈τij对应于轴突信号传输时滞;cij(t)、dij(t)、eij(t)是t时刻的连接权重;Kij(t)是时滞核;Ii(t)表示在t时刻的外部输入。
系统的初始条件为

1 预备工作
定义1:概周期函数。设x(t):ℝ→ℝ,若∀ε〉0,∃l=l(ε)〉0,使在任意长为l的区间内都存在δ,使|x(t+δ)-x(t)|〈ε对任意t∈ℝ都成立,则称x(t)是一个概周期函数。
下面总是假设i,j=1,2,…,n。关于系统,作如下假设:
(H1)存在正常数、,使得0〈ai(t,x)≤,
(H2)存在常数使

(H3)函数fj(·)、gj(·)、hj(·)有界并且满足Lipschitz条件,即存在常数,使得∀x,y∈ℝ,有

2 主要结果
定理1:假设(H1)~(H5)成立,并且有

则系统(2)存在唯一概周期解,并且是全局指数稳定的。
证明:对任意的φ∈X,考虑如下辅助线性系统:
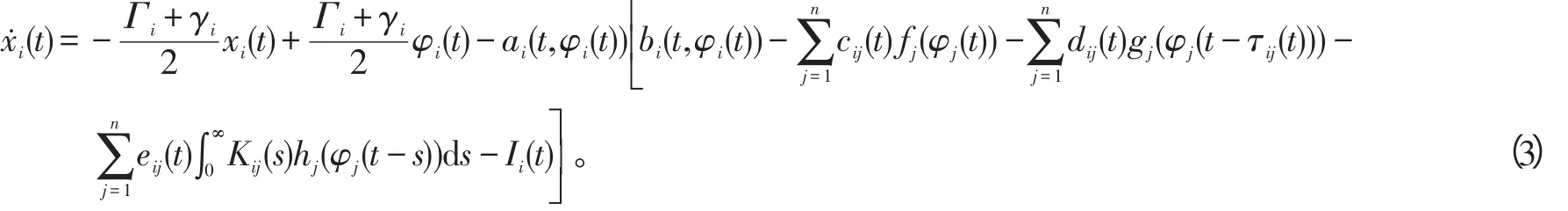
由常数变易法,可得方程的解为:

定义映射

∀φ∈X。令:

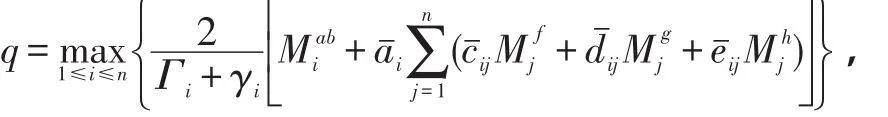
令:

则X*是X的一个闭凸子集。
注意到
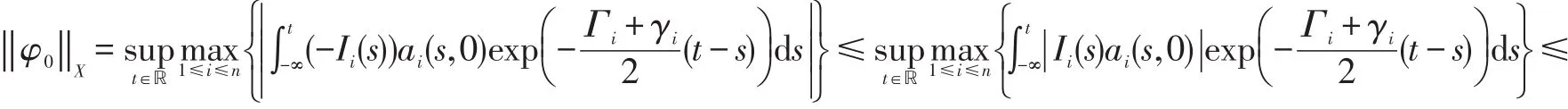
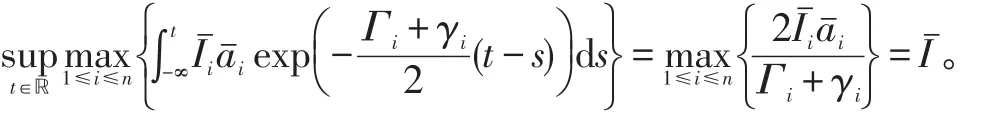
因此,对任意的φ∈X*,有
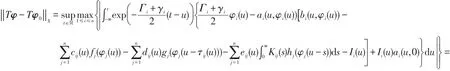

当φi(u)〉0时,由假设(H2)可得

此时有
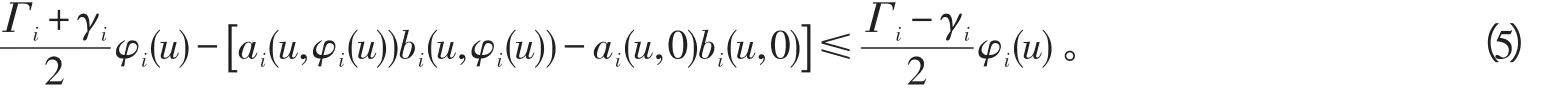
当φi(u)〈0时,由类似的推导可得
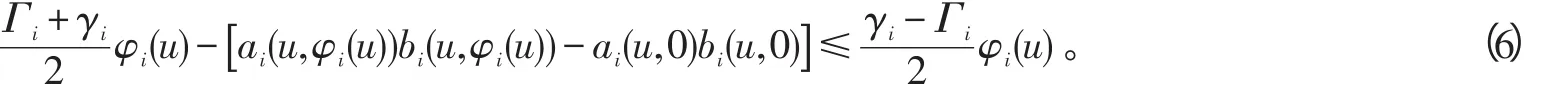
综合式(5)、(6),可以得到

将式(7)代入式(4),有

因此,Tφ∈X*,故T是X*到X*的自映射。接下来证明T是X*到X*的压缩映射。
事实上,对任意φ,ψ∈X*,采用与上面类似的推导过程,可得
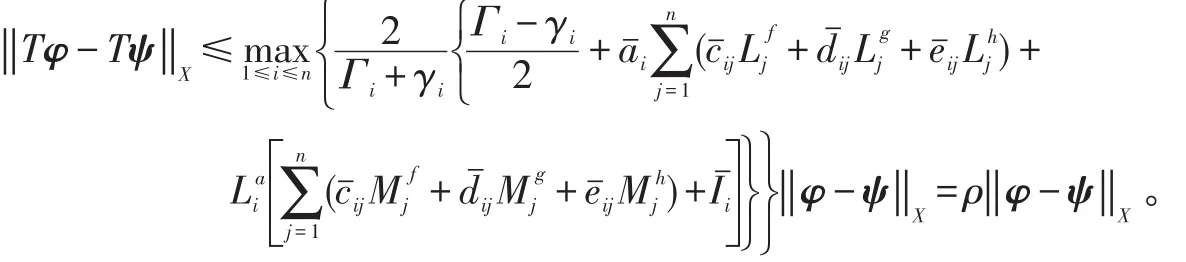
因为ρ〈1,所以T是X*到X*的压缩映射。
由Banach压缩映射不动点定理知,T在X*上有唯一的不动点φ¯,使得Tφ¯=φ¯。由系统的形式可知,系统在X*上存在唯一概周期解x*=φ¯。
接下来证明x*的全局指数稳定性。
令
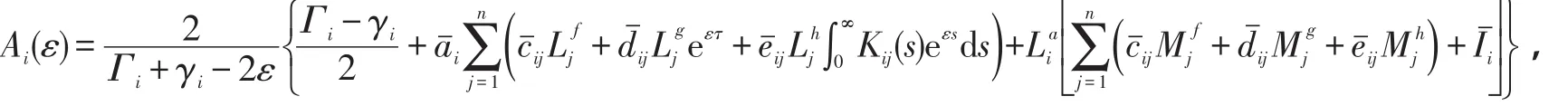
则0〈Ai(0)≤ρ〈1。由Ai(ε)的连续性可知,存在λi〉0,使得0〈Ai(λi)〈1。取λ=1m≤ii≤nn{λi},则有
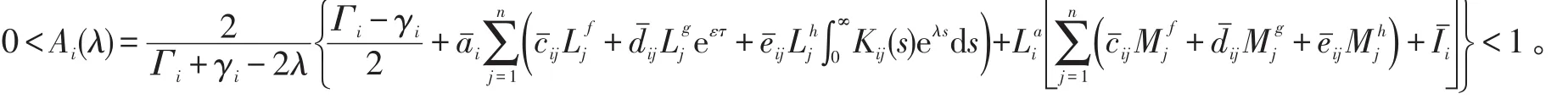
设x(t)是系统(2)的任意一个解,x*(t)是其概周期解,其初始条件分别为
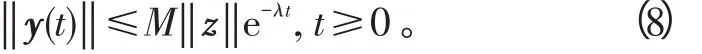
首先证明对任意的α〉1,有下式成立:

当t=0时,式(9)显然成立。
假设当t〉0时式(9)不成立,那么存在t1〉0和i∈{1,2,…,n},使得|,且
注意到,
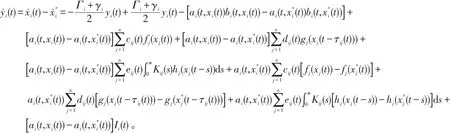
对上述系统利用常数变易法,并由假设(H1)~(H5)和式(7),有
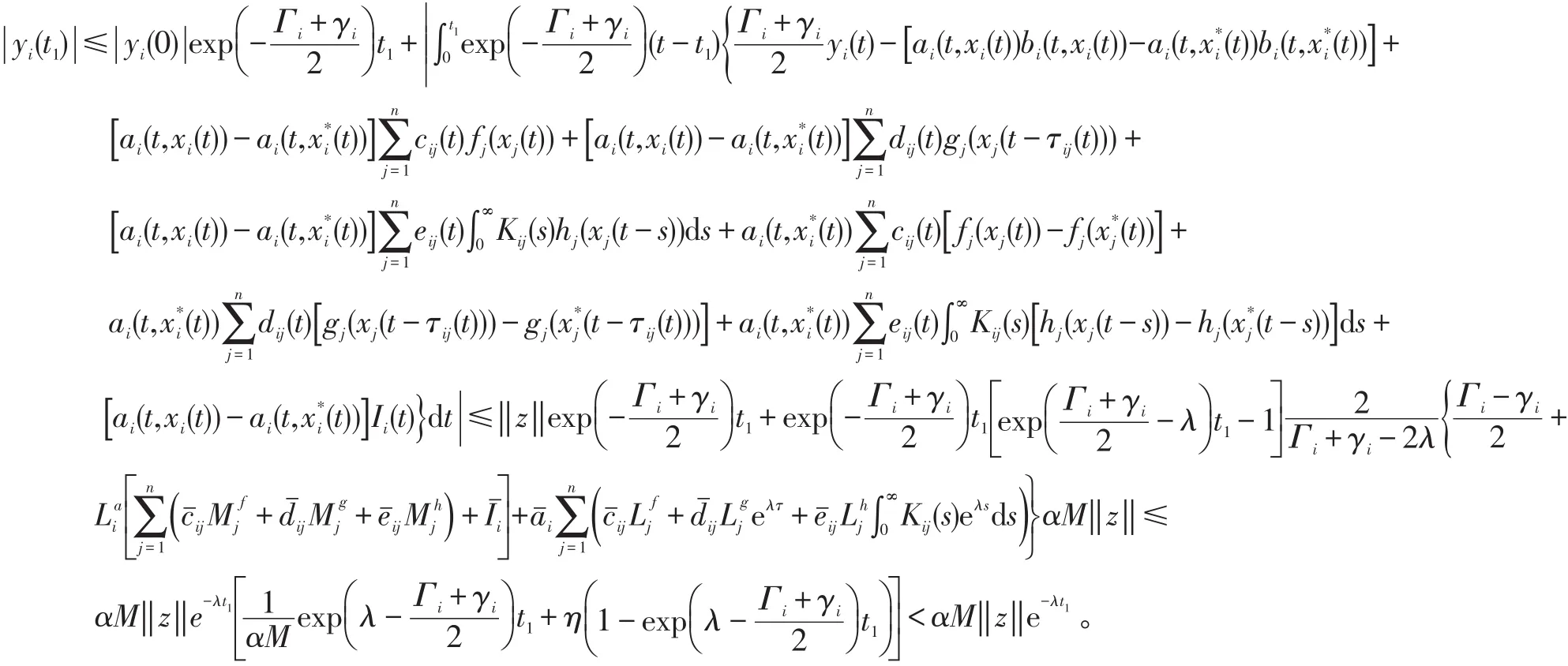
这与假设矛盾,故式(9)成立。令α→1,则有式(8)成立,从而系统的概周期解是全局指数稳定的。
注:若eij(t)≡0,τij(t)=τj,gj=fj,则系统就是文献[13]中所研究的系统,此时文献[13]中的定理1就是本文定理的一个推论。
另外,在文献[13]中,为保证其概周期解的全局指数稳定性,在其定理2中需要加入条件:
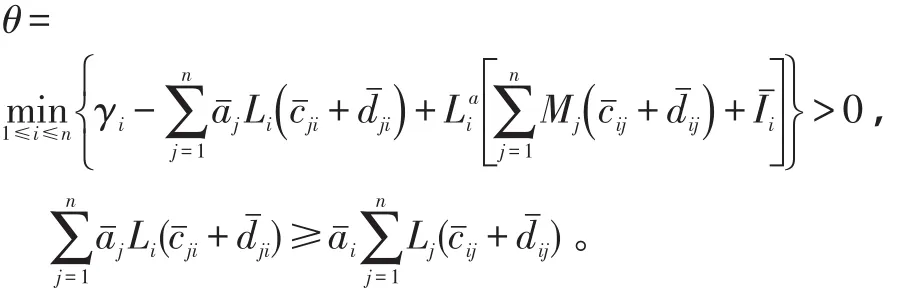
[1] LIU BINGWEN,HUANG LIHONG.Existence and exponential stabilityof almost periodic solutions for Hopfield neural networks with delays[J].Neurocomputing,2005,68:196-207.
[2]LIU BINGWEN.A lmost periodic solutions for Hopfield neural networks with continuously distributed delays[J]. Mathematics and Computers in Simulation,2007,73:327-335.
[3] LIU BINGWEN,HUANG LIHONG.Existence and exponential stability of almost periodic solutions for cellular neural networks with m ixed delays[J].Chaos,Solitons and Fractals,2007,32:95-103.
[4] BAI CHUANZHI.Global stability of almost periodic solutions of Hopfield neural networks with neutral timevarying delays[J].Applied Mathematics and Computation,2008,203:72-79.
[5] XIANG HONGJUN,CAO JINDE.Almost periodic solutions of recurrent neural networks with continuously distributed delays[J].Nonlinear Analysis,2009,71:6097-6108.
[6] XIA YONGHUI,CAO JINDE,LIN MUREN.New results on the existence and uniqueness of almost periodic solution for BAMneural networks with continuously distributed delays[J].Chaos,Solitons and Fractals,2007,31:928-936.
[7] ZHANG HUIYING,XIA YONGHUI.Existence and exponential stability of almost periodic solution for Hopfield-type neural networks with impulse[J].Chaos,Solitons and Fractals,2008,37:1076-1082.
[8] XIAO BING,MENG HUA.Existence and exponential stability of positive almost periodic solutions for high-order Hopfield neural networks[J].Applied Mathematical Modelling,2009,33:532-542.
[9] CHEN ANPING,CAO JINDE.Existence and attractivity of almost periodic solutions for cellular neural networks with distributed delays and variable coefficients[J].Applied Mathematics and Computation,2003,134:125-140.
[10] XIANG HONGJUN,CAO JINDE.A lmost periodic solution of Cohen-Grossberg neural networks with bounded and unbounded delays[J].Nonlinear Analysis:Real World Applications,2009,10:2407-2419.
[11] ZHAO HONGYONG,CHEN LING,MAO ZISEN.Existence and stability of almost periodic solution for Cohen-Grossberg neural networks with variable coefficients[J]. Nonlinear Analysis:Real World Applications,2008,9:663-673.
[12] LI YONGKUN,FAN XUANLONG.Existence and globally exponential stability of almost periodic solution for Cohen-Grossberg BAMneural networks with variable coefficients[J].Applied Mathematical Modelling,2009,33:2114-2120.
[13] CHEN ZHANG,ZHAO DONGHUA,RUAN JIONG.Almost periodic attracor fof Cohen-Grossberg neural networks with delay[J].Physics Letters A,2009,373:434-440.
Almost Periodic Solutions Global Exponential Stability of Cohen-Grossberg Neural Networks
ZHANG Qianga,GAI Ming-jiua,ZHANG Ningb,CUI Shi-weic
(Naval Aeronautical and Astronautical University a.Department of Basic Sciences; b.Department of Training;c.Graduate students'Brigade,Yantai Shandong 264001,China)
In this paper,the existence,uniqueness and global exponential stability of the almost periodic solution for a class of Cohen-Grossberg neural networks were studied,and the sufficient conditions for it's global exponential stability of the unique almost periodic solution was given.The results improvet some present conclusions.
Cohen-Grossberg neural networks;almost periodic solution;stability
TP183;O175
A
1673-1522(2014)04-0374-05
10.7682/j.issn.1673-1522.2014.04.016
2014-03-05;
2014-04-22
张强(1980-),男,讲师,硕士。

