面向异常检测的时间序列树突状细胞算法

田玉玲

(太原理工大学 计算机科学与技术学院，山西 太原 030024)

树突状细胞算法(Dendritic Cell Algorithm，DCA)是针对免疫学中的树突状细胞抽象出的一个与之相对应的数据结构，使用一组异构agent来支持一个二元选择，能够将抗原序列和一系列信号进行组合，实现异常检测．它的根本原理是对抗原数据流和抽象信号形式的多维时间序列进行相关检测，以获得与给定的上下文环境相关度最大的输出结果[1]．树突状细胞算法对未知入侵具有快速、准确的识别能力，适用于对分布式系统进行实时异常检测．树突状细胞算法已经应用于故障诊断、图像分类[2]和异常检测[3]等多种领域中．例如，Amaral[4]提出基于树突状细胞算法的故障检测系统，用于线性非时变电路中的故障检测；Hart等[5]建立了用于自组织无线传感器网络的树突状细胞模型；文献[6]在树突状细胞算法的数据预处理阶段，采用主成分分析(PCA)方法进行降维，自动提取重要特征向量分类到各种指定的信号类型中；文献[7]提出用粗糙集理论中核与约简的概念对树突状细胞算法进行信号特征提取及分类．以上算法的缺点是信号的提取不能根据数据流的变化及时更新，因此不适合用于实时检测系统．

在实际应用中，树突状细胞算法包含较多相互作用的参数，其中各种输入“信号”和“抗原”的概念太抽象和随意，缺乏一个量化的定义．并且随机抽取若干细胞对当前抗原进行采样，随着输入抗原的增加而成熟分化，这种设计策略对抗原的评价计算具有滞后性，导致抗原环境发生转变时误检率较高、检测率降低．

针对异常检测问题，笔者提出了基于时间序列的树突状细胞算法．抗原的定义是全部检测信息构成的矩阵序列，基于多维数据流相关性分析，采用滑动时间窗的变化点检测方法对数据进行检测;利用子空间追踪算法实现抗原数据的采样过程，并通过在算法中加入动态迁移阈值的概念改进算法的识别效率．算法强调对检测数据流的关键变化点的检测分析以及对输入信号的降维处理，使算法能够利用最小的计算空间获得更高的稳定性和检测率．

1 基于时间序列的树突状细胞算法

基于免疫学的树突状细胞算法能够将抗原序列以及一系列信号进行融合，实现异常检测．笔者提出的改进树突状细胞算法，采用变化点检测子空间追踪方法自动对抗原及原始信号进行规格化处理，避免了由任意映射或专家领域知识给定的外部信号干预．算法旨在忽略某些正常数据，而强调某些关键变化点的检测，不仅能根据输入数据流的变化及时更新信号子空间，而且能大规模减少检测数据量，提高了系统的实用性和准确性，为异常检测系统提供了一种新的理论框架．

图1 基于时间序列的树突状细胞算法框架

首先需要对检测数据进行预处理，遴选出能够反映异常状态的关键点数据进行数据流检测分析，并提取特征子集分配到算法的各类输入信号，包括危险信号(DS)、安全信号(SS)和抗原的病原体相关分子模式(Pathogen Associated Molecular Pattern，PAMP)．将所有检测点采集的数据构成矩阵序列作为抗原，并将其标记为变化点的时间序列；截取变化点前后的一个时间段的实时数据，将其定义为当前检测抗原．树突状细胞算法融合处理后的抗原以及各类信号，通过权值计算得到输出信号，根据评估得到抗原所处环境的危险程度，进而采取相应的措施．按照这个过程，显然抗原和输入信号的预处理阶段起着至关重要的作用，它直接影响到算法的检测结果．面向异常检测的时间序列树突状细胞算法的总体框架如图1所示．

基于时间序列的树突状细胞算法主要步骤概括如下:

(1) 基向量压缩．将n个输入数据流采用子空间追踪算法压缩为r个隐含变量的约简表示，其中r≤n．数据子空间中排在最前面的r个基向量的压缩显示了最大变化值．

(2) 更新．在每个新数据点到达的时候更新这种表示，采用了迭代协方差矩阵来增量更新最前r个基向量和隐含变量．这个过程使用一种近似和迭代的方法，算法可以适时更新数据模式．

(3) 信号分类．分别选择包含正常、异常类型相关度高的数据集进行训练，采用变化点子空间追踪方法提取出每一类输入信号的特征子空间向量．

(4) 抗原变化点检测．定义Δ时间内滑动窗口，统计时间序列数据流特征的变化情况，并在下一时间间隔内对上一时间窗口序列值进行修正，从而达到实时检测的目的．

(5) 树突状细胞算法的权值求和．当检测到数据流的相对变化时，标记时间序列的变化点，并将标记变化点的时间序列定义为当前抗原，将当前抗原和输入信号进行权值求和运算，判定异常．

1.1 子空间追踪的信号压缩方法

树突状细胞算法中的“采样”过程，即对当前抗原摄取危险信号、抗原的病原体相关分子模式和安全信号的过程．笔者利用子空间追踪算法实现抗原的“采样”过程，对输入信号进行预处理．使用特征子空间方法，必须在信号数据变化时，能够追踪时变数据和协方差矩阵的特征值和特征向量．算法通过监测所有的n个数据流之间的协方差矩阵Φ的估计值来实现关键变化点的检测[8]．使用降维来构造数据的约简表示，然后当新的数据点到达时，将迭代地更新该子空间，并随着时间的推移逐渐遗忘旧的数据样本．因此，它检测到的变化是所有数据流的相对变化，而不是每个单独数据流的历史变化．

定义一个独立随机序列{Xn}，表示在T时间内出现的检测数据流，对X1，X2，…，Xi，…，Xn进行检测，其中i为未知变化点，1≤i≤n．设k=n-i，表示时间窗为n的具有p个属性的多维数据流．子空间追踪算法大部分都是基于正交迭代的原则，将正交迭代应用于协方差矩阵中．子空间追踪的主要目标是递归r个主要特征值以及时间递归更新协方差矩阵相关的特征向量，如下所示:

Φ(t)=αΦ(t-1)+X(t)XT(t) ,

(1)

其中，t时刻数据流之间的协方差矩阵为Φ，X(t)是在t时刻n个数据流的输入数据向量；α是一个正的指数遗忘因子，0<α<1．然后，在每个时间步长利用一个正交迭代，即

其中，A(t)是一个p×r的辅助矩阵，Q(t)是包含r个估计主特征向量的n×r矩阵，S(t)是以降序排列的估计特征向量的r×r上三角矩阵．

为了获得一个适度的子空间传播模型来完成递归，引入下面的状态空间形式:

Q(t)=Q(t-1)Θ(t)+Δ(t) ,

(3)

其中，Δ(t)是一个满足

QT(t-1)Δ(t)=0

(4)

的修正矩阵；Θ(t)是子空间转置矩阵，将其表示为

Θ(t)=QT(t-1)Q(t) ．

(5)

给定主特征的基向量，数据向量X(t)可以被压缩到一个低维表示，即

h(t)=QT(t-1)X(t) ,

(6)

其中，h(t)向量描述了r个隐含变量．

将式(1)和式(3)代入式(2a)中，并经过约简可得辅助矩阵A(t)，即

A(t)=αA(t-1)Θ(t-1)+X(t)hT(t) ．

(7)

由式(2b)可知辅助矩阵A(t)也是一个正交分解问题，则可用以下公式更新正交分解:

Q(t)S(t)=αQ(t-1)S(t-1)Θ(t-1)+X(t)hT(t) ．

(8)

根据以上描述，在每个时间步长迭代地更新Q，S矩阵，用这些结果来计算压缩投影或隐含变量h(t)；然后，使用这些主特征向量将原始数据约简，从而得到原始数据的低秩近似值．

1.2 变化点检测的抗原定义

异常总是与输入数据的变化相关联，变化点是候选的异常事件，但是一些变化点也对应着输入数据中正常的周期性变化．采用时间序列变化点检测，对一个随机过程{Xn}，以顺序的方式获得时间序列，检测时间序列是否在统计分布规律上发生变化．当异常发生时，网络数据的多个特征通常会同时发生变化，通过标记特征变化情况，能够有效地放大异常数据流与正常数据流之间的差异，提高检测精度．

为了检测网络异常，采用滑动窗口无参数CUSUM检测算法在线检测并行的多维数据流[9]．CUSUM方法能够快速地反映出数据流特征的变化情况，无须建立数学模型，并在下一时间间隔内对序列值进行修正，得到更准确的检测序列值．算法只累积一定窗口时间内的输入数据流和在此期间出现的异常变化点个数，当它们超过一定的阈值时，则表明有异常发生．

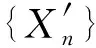
设在一定时间窗T内，共包含有m个Δt，则滑动窗口内Xn的累积值yn表示为

(9)

用以下递归定义提高计算效率:

(10)

其中，y0=0，yn表示在窗口时间T内出现的变化点个数，x+定义为

(11)

设报警阈值为λ，则判断异常的函数为

(12)

当yn超过阈值λ时，检测到变化，在这个时间步长中标记变化，并且所有累积变量复位．

1.3 输入输出信号关联关系

一旦预处理信号类型的特征被确定，下一步进行树突状细胞算法的输入输出关联、上下文评价和树突状细胞分类等过程．对输入信号进行预处理是为了获得以下输出信号:

(1) 协同刺激分子值(csm): 用于判定细胞是否进行状态转换;

(2) 半成熟细胞因子(semi): 用于判定细胞的“安全程度”;

(3) 成熟细胞因子(mat): 用于判定细胞的“危险程度”．

根据输入信号计算输出信号，采用标准树突状细胞算法的加权求和方法进行输入输出信号相关性处理，利用以下带权计算公式:

(13)

其中，O[k]表示输出信号(O[0]～O[2]依次表示csm、semi、mat)，Si表示输入信号(S0～S2依次表示抗原的病原体相关分子模式、DS、SS)，Wij表示从Si到Oj的相应信号权值．权值可以根据具体的应用环境进行调整．

1.4 上下文评估

树突状细胞是根据协同刺激分子值O[0]的大小进行状态转换，并进一步对抗原进行危险度判定的．O[0]值的计算需要一个累加的过程．对于排在细胞集尾部的数据，有可能因O[0]值未达到迁移阈值而导致细胞无法成熟，因此需多次迭代运行．然而树突状细胞算法的多次迭代并不能有效地提高检测精度，只是为了完成对边界数据的评价处理．

笔者对树突状细胞算法的评估方法进行改进，在算法中加入动态迁移阈值的概念，通过控制未成熟树突状细胞(iDC)的迁移阈值，加速或者减缓未成熟树突状细胞的分化成熟，有效改进算法的检测效率．加入数据变化点之后的 (n-i) 个抗原数据为Xi+1，Xi+2，…，Xn．设当前抗原的评估系数为β，Ai为抗原特征向量，计算每个后续抗原与当前变化点抗原的亲和力D为

设动态迁移阈值为mt，树突状细胞的迁移状态由评估系数β进行调节．若评估系数β很小，则后续抗原延续了当前变化点抗原的变化状态，上调mt以减缓未成熟树突状细胞的成熟，继续采样后续抗原．动态迁移阈值定义为

mt(t)=mt(t-1)+Δ(β) ,

(16)

其中，Δ(β)是β的相关增量．β越大，表示后续抗原与当前抗原的状态越相异，根据式(16)调整mt，加速未成熟树突状细胞成熟，防止其截取到后续抗原，从而有效地降低了数据误分类的可能．设输出信号O[0]的值为Zcsm，若Zcsm>mt(t)，则当前未成熟树突状细胞成熟并迁移出细胞库．

下一步，计算成熟环境抗原值V，并对当前抗原进行评价:

V=O[2]/(O[1]+O[2]) ．

(17)

2 实验及仿真

实验数据采用KDD CUP 1999入侵检测标准数据集[10]．其中异常数据分为39种入侵类型，训练集中包含22种入侵类型，另外的17种预先未知的入侵类型包含在测试集中．网络连接记录包含41个属性，其中包括34个连续形式的属性和7个离散形式的属性．实验采用了该数据集的一个10%的子集(kddcup.data10percentcorrected)，选取 2 396 条测试数据，选择12 种入侵模式，使用41个属性．实验环境采用Matlab 2011a、windows 7、Visual C++6.0 作为仿真测试工具平台．

2.1 信号预处理测试

首先对变化点特征提取的子空间算法进行验证．设定数据流数目n=20，指数遗忘因子α=0.996，每个时间步长t=3 000，分别用主成分分析算法、基于压缩的投影近似子空间跟踪算法(PASTd)和笔者提出的变化点子空间追踪(CPD)算法对测试数据流进行降维处理，分析了3种算法的降维效果，并进行了对比，图2的(a)～(d)分别显示了原始数据集分布和各种算法降维结果的数据分布．

图2 不同算法降维结果的数据分布图

2.2 检测测试

表1 改进树突状细胞算法的检测实验结果

用8组测试数据对标准树突状细胞算法、PCA-DCA算法(主成分分析-树突细胞算法)和笔者提出的CPD-DCA算法进行检测，对3种算法使用相同的测试数据进行检测．在经历环境状态变化时，抗原数目不断增加的平均检测率对比关系如图3所示．3种算法分别在进化过程中所占存储空间比例的对比如图4所示．

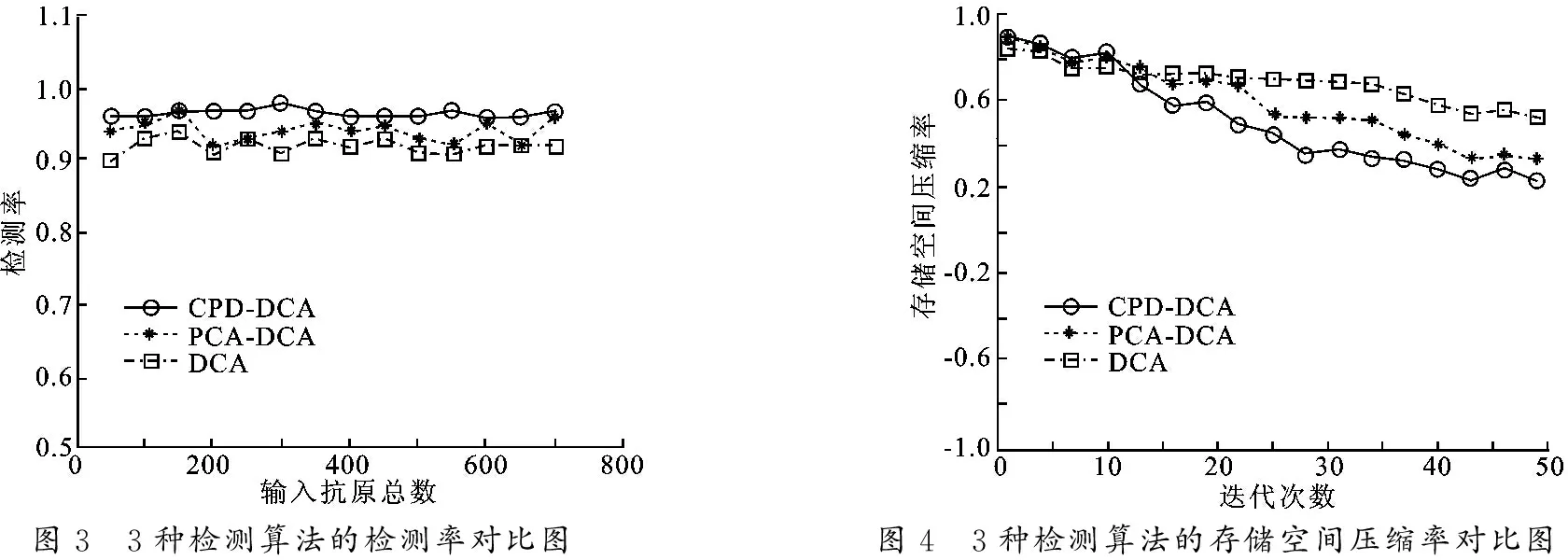
图3 3种检测算法的检测率对比图图4 3种检测算法的存储空间压缩率对比图

从图3可以看出，树突状细胞算法和PCA-DCA算法的检测率有明显的波动，对比而言，CPD-DCA算法整体检测率高于其他两种算法，且稳定性较好，CPD-DCA算法可以维持在一个较高的识别率状态．由于在算法运行过程中，输入信号的维数迭代降低(见图4)，内存消耗随维数的降低而减少， 主要受维度的影响，CPD-DCA算法的存储空间利用率明显高于其他两种算法．

3 总 结

在树突状细胞算法中，由于缺乏一个对信号和抗原的可量化定义，导致在实际应用中对树突状细胞算法的各种主观输入的指定和人为参数设置．笔者提出了基于变化点子空间追踪的信号特征降维算法，根据异常训练数据自动提取相关度最高的特征构成树突状细胞算法的输入信号；采用了滑动时间窗CUSUM检测方法，对抗原的检测只强调数据流关键变化点的检测以及在上下文评估中加入迁移阈值的动态性，在很大程度上降低了计算空间，同时保证了更加准确和稳定的检测效率，具有较好的实际操作性．实验证明，算法不仅具有准确性高、检测率高、消耗计算资源少的特点，而且能够区分正常数据变化与异常，并可以在入侵出现的早期检测出异常的存在．

[1] Greensmith J. The Dendritic Cell Algorithm [D]. Nottingham: University of Nottingham, 2007.

[2] 王凌霞, 焦李成, 颜学颖, 等. 利用免疫克隆进行小波域遥感图像变化检测[J]. 西安电子科技大学学报, 2013, 40(4): 108-113.

Wang Lingxia, Jiao Licheng, Yan Xueying, et al. Change Detection in Multi-temporal Remote Sensing Images Based on the Wavelet-domain Immune Clonal Optimazition[J]. Journal of Xidian University, 2013, 40(4): 108-113.

[3] Gu F. Theoretical and Empirical Extensions of the Dendritic Cell Algorithm [D]. Nottingham: University of Nottingham, 2011.

[4] Amaral J L M. Fault Detection in Analog Circuits Using a Fuzzy Dendritic Cell Algorithm[C]//Proceedings of the 10th International Conference on Artificial Immune Systems: 6825. Heidelberg: Springer, 2011: 294-307.

[5] Hart E, Davoudani D. An Engineering-informed Modelling Approach to AIS[C]//Proceedings of the 10th International Conference on Artificial Immune Systems: 6825. Heidelberg: Springer, 2011: 240-253.

[6] Gu F, Greensmith J, Oates R, et al. PCA 4 DCA: the Application of Principal Component Analysis to the Dendritic Cell Algorithm[C]//Proceedings of the 9th Annual Workshop on Computational Intelligence. Nottingham: University of Nottingham, 2009: 352-358.

[7] Chelly Z, Elouedi Z. RC-DCA: a New Feature Selection and Signal Categorization Technique for the Dendritic Cell Algorithm Based on Rough Set Theory[C]//Proceedings of the 11th International Conference on Artificial Immune Systems: 7597. Heidelberg: Springer, 2012: 152-165.

[8] Strobach P. The Fast Recursive Row-Householder Subspace Tracking Algorithm [J]. Signal Processing, 2009, 89(12): 2514-2528.

[9] Bassevilleand M, Nikiforov I V. Detection of Abrupt Changes: Theory and Application[M]. New Jersey: Prentice Hall, 1993.

[10] Stolfo S J, Fan W, Lee W, et al.KddCup 1999 Data[DB/OL]. [2013-01-30]. http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html.