一种采用并行免疫优化的频谱分配算法
吴慧欣, 王 秉, 柴争义
(1. 华北水利水电大学 信息工程学院,河南 郑州 450011; 2. 河南交通职业技术学院 航运海事系,河南 郑州 450005; 3. 天津工业大学 计算机科学与软件学院,天津 300387; 4. 东南大学 移动通信国家重点实验室,江苏 南京 210096)
无线频谱是不可再生的稀缺资源.随着无线通信业务的迅速发展,无线频谱资源愈发紧缺.已有的研究表明,固定频谱管理体制造成了频谱资源的巨大浪费[1].在认知无线网络中,认知用户(次用户)通过对授权用户(主用户)授权频谱的“二次利用”,有效地提高了频谱使用效率,被认为是目前解决频谱资源供需矛盾的最有效途径之一[2-3].
频谱分配是提高频谱利用率的关键问题之一.频谱分配的主要目的是在认知用户、网络QOS等需求下,有效分配可用频谱资源,达到最优状态.针对不同的应用场景,现有的频谱分配方法主要包括博弈论、拍卖理论以及图着色理论等[4].笔者主要研究基于合作的分布式完全受限频谱分配算法,是基于图着色理论实现的.在基于图论的已有研究中,颜色敏感图着色(Color Sensitive Graph Coloring,CSGC)算法[5]是最具代表性的成果之一,详细地给出了基于图论的频谱分配模型,并对效益和公平性进行了较详尽的分析.基于图论的频谱分配是一个优化问题,其最优着色算法是一个NP难问题[6],智能优化是求解此类问题的有效途径.为了降低算法的复杂度,文献[6]将遗传算法引入频谱分配,实现了较好的分配结果并降低了求解复杂度.此后,免疫算法[7]、粒子群算法[8]、蚁群算法[9]等智能算法相继用来提高求解效果.
然而,已有的算法更多地关注网络的总体收益,对如何减少算法运行时间的研究并不多.实际上,由于可用频谱信息的动态变化,实时性要求是认知无线网络频谱分配区别于其他无线通信频谱分配的最重要特点之一,因此,频谱分配时间应该尽可能短.基于此,笔者提出一种基于并行免疫的频谱分配算法,减少算法的计算时间.
1 认知无线网络的频谱分配模型
认知无线网络频谱分配模型可用以下矩阵表示[4-9]: 可用频谱矩阵L、效益矩阵B、干扰矩阵C和分配矩阵A.
假设有N个认知用户,可用频谱数为M,频谱间相互正交.对各个矩阵说明如下:
(1) 可用频谱矩阵L.可用频谱矩阵L={ln,m|ln,m∈{0,1}}N×M.当ln,m=1 时,表示认知用户n(1≤n≤N) 可以使用频谱m(1≤m≤M) ;当ln,m=0 时,表示认知用户n不能使用频谱m.
(2) 效益矩阵B.在同一个可用频谱上,不同的认知用户获得的效益用效益矩阵B={bn,m}N×M表示,即用户n(1≤n≤N) 使用频谱m(1≤m≤M) 后得到的收益.很显然,当ln,m=0 时,必有bn,m=0,即只有可用频谱才有效益矩阵.
(3) 干扰矩阵C.不同的认知用户使用同一可用频谱可能产生干扰,用干扰矩阵C表示,C= {cn,k,m|cn,k,m∈{0,1}}N×N×M.当cn,k,m=1 时,表示认知用户n和k(1≤n,k≤N) 同时使用频谱m(1≤m≤M) 会产生干扰;反之,当cn,k,m=0 时,干扰矩阵C由可用频谱矩阵L决定.当n=k时,cn,n,m= 1-ln,m,并且满足cn,k,m≤ln,mlk,m,即只有频谱m同时对认知用户n和k可用时,才可能产生干扰.
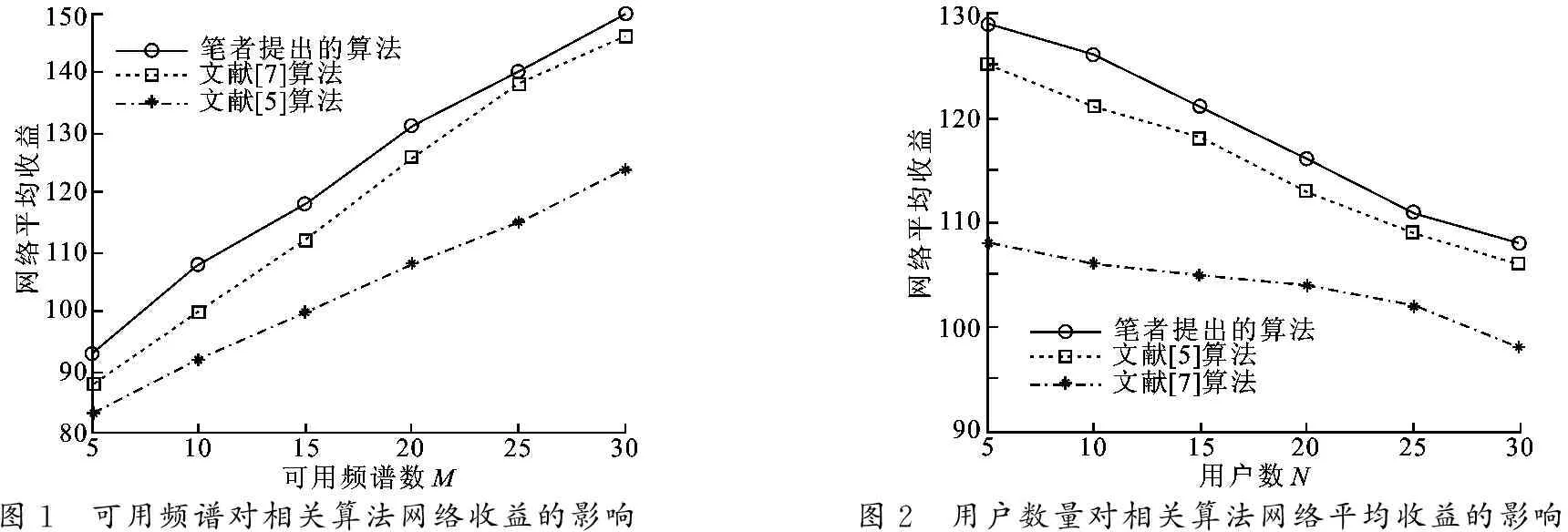
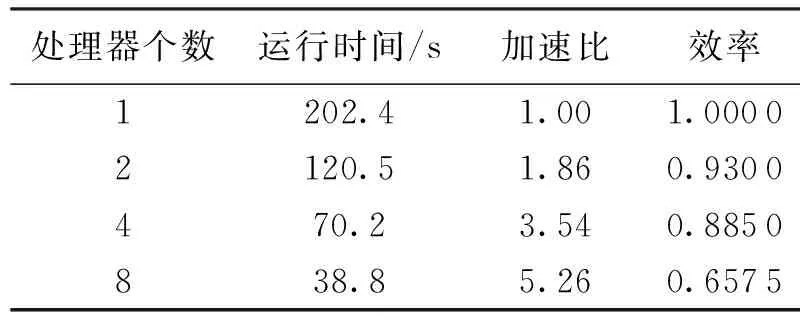
(4) 无干扰分配矩阵A.将可用、无干扰的频谱分配给认知用户,得到无干扰分配矩阵A= {an,m|an,m∈{0,1}}N×M.当an,m=1 时,表示将频谱m分配给认知用户n;反之,an,m=0.分配矩阵必须满足C定义的如下约束条件:an,m×ak,m=0, 如果cn,k,m=1,∀n,k 从上面的描述可知,满足条件的分配矩阵A不止一个,用∧NM表示所有A的集合.给定某一无干扰频谱分配矩阵A,次用户n获得的总收益用效益向量R表示为 频谱分配的目标是最大化网络效益U(R),则可表示为如下所示的优化问题: 其中,arg(·)表示求解网络效益最大时所对应的频谱分配矩阵A.因此,A*即为所求的最优无干扰频谱分配矩阵. U(R)有不同的表示形式[4-9],考虑到流量和公平性需求,这里U(R)定义为平均最大化网络收益总和: 在智能优化中,为了加快算法的收敛速度,同时又不希望牺牲种群的多样性,算法的并行实现是一个有效途径.人工免疫优化的并行化模型主要借鉴进化算法实现,有主从式并行模型、粗粒度并行模型及细粒度并行模型[10-12].笔者采用简单易实现的主从式并行模型.主从式是一种单种群进化模型,分为主进程和从进程,主进程执行进化操作算子,从进程分别计算每个抗体的亲和度值,主进程和从进程交替工作. 在人工免疫优化中,抗体映射为问题的候选解,免疫优化算法通过初始化、亲和度评价、克隆扩增、克隆变异、克隆选择等过程对抗体进行优化,最终得到所需的解[13-14].对免疫优化算法而言,传统的串行算法在克隆个体后,循环计算每个个体的亲和度.在并行计算中,可以把循环进行分解,也就是把要计算适应度的个体通过消息发送到集群中的多个节点中,然后并行计算亲和度,最后各个节点把计算好的亲和度传送回来. 并行算法流程简单描述如下: (1) 主节点获得处理器(CPU)个数X和种群规模Y. (2) 计算每个节点要计算的个体数目Z.每个处理器要计算的个体(向下取整),剩余的个体发送给编号较大的处理器.因此,每个处理器接收到的个体数目最多只相差一个. (3) 主节点发送个体编码到从节点,各个从节点并行计算亲和度并发送回主节点,主节点接收从节点返回的亲和度值. 从上面的描述可知,频谱分配问题具体描述为: 在可用频谱矩阵L、效益矩阵B、干扰矩阵C已知的情况,如何找到最优的频谱分配矩阵A,使得网络效益U(R)最大. 针对频谱分配问题,笔者设计的免疫优化算法关键技术说明如下: (2) 抗体编码表示到分配矩阵A的映射.分别记录矩阵L中值为1的元素对应的n与m,并将其按照先n递增、后m递增的方式保存在L1中,即L1= {(n,m)|ln,m=1}.显然,L1中元素个数为l.将种群中每个抗体的每一位j(1≤j≤l) 映射为矩阵A的元素an,m,其中(n,m)的值为L1中相应的第j个元素j(1≤j≤l). (3) 亲和度函数的表示.由于频谱分配的目标是实现最大化网络效益U(R),故直接将U(R)作为亲和度函数. 算法的基本步骤如下(其中,P表示抗体种群,p表示一个抗体). 步骤1 初始化.设进化代数g为零,种群规模为s,按照前面所述的编码方式,随机初始化种群P(g)= {p1(g),p2(g),…,ps(g)}. 步骤2 抗体表示到频谱分配方案的映射.通过抗体映射方式,将每一个抗体映射为相应的分配矩阵A,即为一种可能的频谱分配方案. 步骤3 干扰约束的处理.随机产生的抗体所对应的分配矩阵A不一定满足干扰矩阵C,所以,必须进行修正.具体实现如下: 对任意m,如果cn,k,m=1,则查看矩阵A中第m列的第n行和第k行元素值是否同时为1.若是,则随机将其中一位置零,另一位保持不变.此时得到的分配矩阵A则为经过约束处理的可行解;同时,对相应的抗体表示进行映射,更新P(g). 步骤4 按照上面所示的并行化过程对P(g)进行亲合度函数评价.对P(g)中的s个抗体进行亲和度计算,结果按从大到小降序排序,亲和度最大的抗体所对应的分配矩阵A即为所求的最优频谱分配方案. 步骤5 终止条件判断.如果达到设置的最大进化次数gmax,则算法终止,将抗体种群中亲和度最高的抗体映射为A的形式,即得到了最佳的频谱分配;否则,转步骤6. 在并行计算实验室HPC集群机上进行了仿真.集群有1个管理节点,1个I/O节点, 32个常规计算节点,操作系统为RedHat Enterprise Linux AS,使用C+MPI进行编程实现.MPI是消息传递模型的国际标准[10].在实验过程中,L、B、C矩阵的生成采用文献[5]附录1提供的伪代码产生,并且保证其满足相应的约束.免疫算法中参数的取值如下: 最大进化代数gmax=200,种群规模s=20,变异概率pm=0.1,克隆规模控制参数nc=5,使用的处理器个数为1~8个. 为了验证本算法的性能,与目前求解频谱分配问题经典的CSGC算法[5]及本课题前期的免疫克隆选择算法进行了比较[7].这两个算法是串行算法,在I/O节点上运行.实验结果使用网络收益总和来衡量.为了公平起见,在算法比较试验中,使用代码产生相同的L、B、C,使用同样的参数设置,并将算法运行50次,取平均结果.表1是50次实验所得到的平均收益,其中分别选M=N=5 和M=N=20 (M表示可用频谱,N表示认知用户).从表1中可以看出,笔者提出的算法在网络收益上高于对比算法.同时,也可以看出,随着迭代次数的增加(CSCG是确定性算法,不随迭代次数变化),笔者提出的算法收敛速度快于串行免疫算法的收敛速度,说明了笔者提出的算法有较快的求解速度. 表1 网络收益比较 为了进一步对比算法的性能,实验验证了在认知用户N固定的情况下,随着可用频谱M的增加,相关算法的性能变化.这里取N=10,结果如图1所示. 图1 可用频谱对相关算法网络收益的影响图2 用户数量对相关算法网络平均收益的影响 从图1可以看出,随着可用频谱数M的增加,网络收益一直在递增.笔者提出的算法在收益增加方面优于另外两种算法,进一步表明了笔者提出的算法的有效性.同时,实验也验证了在可用频谱M已知的情况下,认知用户数变化对网络收益的影响,结果如图2所示.实验结果表明:随着认知用户数的增加,系统收益降低,但笔者提出的算法得到的收益高于另外两种算法,证明了笔者提出的算法的优越性. 衡量并行算法相对收益的指标一般使用加速比和效率分析[10-12].加速比sp=ts/tp,其中ts是求解一个问题的串行算法的运行时间,tp是求解同一个问题的并行算法的运行时间.可见,加速比是算法的并行性对运行时间改进的程度.效率Ep=sp/p,其中p为处理器的个数,效率反映了并行系统中处理器的有效利用情况.这里使用笔者提出的算法和串行免疫克隆算法[7]进行比较. 表2 算法并行效果 表2所示是在不同处理器个数下频谱分配算法运行时间、加速比、效率的情况. 频谱分配是认知无线网络中的关键问题之一,而实时性是其显著特点之一.笔者提出了一种基于并行免疫优化的频谱分配算法,缩短了算法分配时间,对认知频谱分配的实时性有促进意义.下一步将继续研究并行免疫优化算法的并行模型、子种群规模和计算能力之间的关系.此外,负载均衡和程序优化等也还需要进一步的研究. [1] Akyildlz I F, Lee W Y, Vuran M C, et al. Next Generation/dynamic Spectrum Access/cognitive Radio Wireless Networks: a Survey [J]. Computer Networks, 2006, 50(13): 2127-2159. [2] 魏急波, 王杉, 赵海涛. 认知无线网络: 关键技术与研究现状[J]. 通信学报, 2011, 32(11): 147-158. Wei Jibo, Wang Shan, Zhao Haitao. Cognitive Wireless Networks: Key Techniques and Sate of the Art[J]. Journal on Communications, 2011, 32(11): 147-158. [3] Wang Beibei, Liu K J R. Advances in Cognitive Radio Networks: a Survey[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(1): 5-23. [4] 王钦辉, 叶保留, 田宇, 等. 认知无线电网络中频谱分配算法[J]. 电子学报, 2012, 40(1): 147-154. Wang Qinhui, Ye Baoliu, Tian Yu, et al. Survey on Spectrum Allocation Algorithms for Cognitive Radio Networks[J]. Acta Electronica Sinica, 2012, 40(1): 147-154. [5] Peng Chunyi , Zheng Haitao, Zhao Benyi. Utilization and Fairness in Spectrum Assignment for Opportunistic Spectrum Access[J]. Mobile Networks and Applications, 2006, 11(4): 555-576. [6] Zhao Zhijin, Peng Zhen, Zheng Shilian. Cognitive Radio Spectrum Allocation Using Evolutionary Algorithms[J]. IEEE Transactions on Wireless Communications, 2009, 8(9): 4421-4425. [7] 柴争义, 刘芳. 基于免疫克隆选择优化的认知无线网络频谱分配[J]. 通信学报, 2010, 31(11): 91-100. Chai Zhengyi, Liu Fang. Spectrum Allocation of Cognitive Wireless Network Based on Immune Clone Selection Optimization[J]. Journal on Communications, 2010, 31(11): 91-100. [8] Tang Meiqin, Long Chengnian, Guan Xinping, et al. Nonconvex Dynamic Spectrum Allocation for Cognitive Radio Networks Via Particle Swarm Optimization and Simulated Annealing[J]. Computer Networks, 2012, 56(11): 2690-2699. [9] 杨淼, 安建平. 认知无线网络中一种基于蚁群优化的频谱分配算法[J]. 电子与信息学报, 2011, 33(10): 2306-2311 Yang Miao, An Jianping. An Ant Colony Optimization Algorithm for Spectrum Assignment in Cognitive Radio Networks[J]. Journal of Electronics & Information Technology, 2011, 33(10): 2306-2311. [10] 朱虎明, 焦李成. 并行免疫克隆特征选择算法[J]. 西安电子科技大学学报, 2008, 35(5): 853-857. Zhu Huming, Jiao Licheng. Parallel Immune Clonal Selection for Feature Selection[J]. Journal of Xidian University, 2008, 35(5): 853-857. [11] Jacobsen D A. Senocak I. Multi-level Parallelism for Incompressible Flow Computations on GPU Clusters[J]. Parallel Computing, 2013, 39(1): 1-20. [12] 戚玉涛, 焦李成, 刘芳. 基于并行人工免疫算法的大规模TSP问题求解[J]. 电子学报, 2008, 36(8): 1552-1558. Qi Yutao, Jiao Licheng, Liu Fang. Parallel Artificial Immune Algorithm for Large-Scale TSP[J]. Acta Electronica Sinica, 2008, 36(8):1552-1558. [13] 尚荣华, 焦李成, 胡朝旭, 等. 修正免疫克隆约束多目标优化算法[J]. 软件学报, 2012, 23(7): 1773-1786. Shang Ronghua, Jiao Licheng, Hu Chaoxu, et al. Modified Immune Clonal Constrained Multi-Objective Optimization Algorithm[J]. Journal of Software, 2012, 23(7): 1773-1786. [14] 王凌霞, 焦李成, 颜学颖, 等. 利用免疫克隆进行小波域遥感图像变化检测[J]. 西安电子科技大学学报, 2013, 40(4): 108-113. Wang Lingxia, Jiao Licheng, Yan Xueying, et al. Change Detection in Multi-temporal Remote Sensing Images Based on the Wavelet-domain Immune Clonal Optimazition[J]. Journal of Xidian University, 2013, 40(4): 108-113. [15] Gong Maoguo, Chen Xiaowei, Ma Lijia, et al. Identification of Multi-resolution Network Structures with Multi-objective Immune Algorithm[J]. Applied Soft Computing, 2013, 13(4): 1705-1717. [16] Gong Maoguo, Zhang Lingjun, Ma Jingjing, et al. Community Detection in Dynamic Social Networks Based on Multiobjective Immune Algorithm[J]. Journal of Computer Science and Technology, 2012, 27(3): 455-467.2 并行免疫优化算法的主要思想
3 基于并行免疫优化的频谱分配实现技术
3.1 关键技术
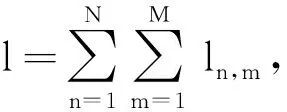
3.2 算法实现步骤
4 仿真实验与结果分析
4.1 算法仿真环境和参数设置
4.2 实验结果及分析

4.3 并行算法的性能分析

5 总结与展望

