融合卡方累积分布函数和PDE的曲波阈值去噪法

崔 华， 严玍伻

(长安大学 信息工程学院，陕西 西安 710064)

曲波阈值去噪框架[1-2]中不同的阈值函数产生不同的去噪效果．文献[3]中所述的软阈值和硬阈值函数得到了广泛应用，但它们都存在不同程度的缺陷．曲波硬阈值函数在阈值点处的不连续造成去噪图像有明显的振铃、伪吉布斯效应等视觉失真．曲波软阈值函数处理前后的曲波系数之间存在恒定偏差，导致图像的边缘模糊，造成去噪图像视觉质量降低．所以，构造高效的阈值函数是改善曲波阈值去噪法去噪性能的关键[4-6]．另外，曲波阈值去噪法只能保证绝对值小于阈值的噪声被去掉[1,4]，而且阈值选择没有统一标准，还会出现环绕效应，导致图像视觉质量差[5-6]．针对曲波阈值去噪法本身固有的这些性能缺陷，笔者将基于信息融合思想利用偏微分方程(Partial Differential Equation, PDE)[7-8]来改善曲波阈值方法的去噪效果[9]．

1 基于卡方累积分布函数的曲波阈值函数

含噪图像可以表示为

y=x+δu,

(1)

其中，x和y分别表示原图像和含噪图像；u～N(0，1)，为标准高斯白噪声；δ是噪声方差．高斯白噪声的一个重要特点是对其进行曲波分解[2]后，其曲波子带系数也呈现正态分布特性，所以可以考虑采用与正态分布相关的数学函数来构造曲波阈值函数．这里利用卡方分布的累积分布函数[10]构建新的曲波阈值函数，其表达式为

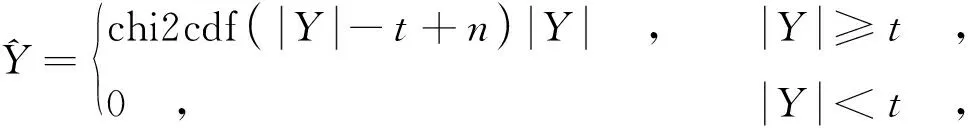
(2)

(3)

图1 基于卡方累积分布函数的曲波阈值函数

2 融合PDE扩散的新曲波阈值去噪法

对于曲波阈值去噪法本身固有的环绕效应和难以兼顾去噪效果与保留细节的弊端，新曲波阈值去噪法同样需要克服．文中利用信息融合方法来解决．PDE扩散[7-9]与曲波阈值去噪法分别以不同的去噪机制对含噪图像进行去噪处理，二者的去噪结果是对真实图像、噪声和图像细节的不同表达．文献[8]所述的非线性结构张量扩散PDE中包含着新阈值函数丢失的有用信息，将它们融合到新曲波阈值去噪图像中，势必能改善其去噪性能[9]．具体融合方案如下所述．

对同一含噪图像，由新曲波阈值去噪法和文献[8]所述的非线性结构张量扩散PDE得到的去噪图像可以看成是干净图像与噪声的叠加，即

其中，x表示干净图像；y1和y2分别表示新曲波阈值和PDE去噪法得到的去噪图像；ε1和ε2表示去噪图像中包含的噪声，噪声ε1包括新曲波阈值去噪法引起的图像振铃、伪吉布斯效应等视觉失真的干扰以及该方法丢失的细节和未处理干净的残余噪声．噪声ε2由偏微分方程去噪法造成的图像边缘模糊、边缘位置移动等现象的干扰、丢失的细节以及未处理干净的残余噪声组成．由于ε2与ε1产生的机制不同，对干净图像x的影响也不同，ε2中包含一些对削减噪声ε1有用的信息，如果将ε2叠加到ε1上，就能进一步改善y1的信噪比．其次，ε2与ε1在x上的分布也不同，如果将ε2叠加到ε1上，就可以降低图像y1形变的集中程度，改善y1的视觉效果．另外，ε2与ε1中所包含的图像细节不同，如果将ε2叠加到ε1上，就可以改善y1的视觉质量．为此，将偏微分方程去噪图像叠加融合到曲波阈值去噪图像中，可表示为

y3=λy1+(1-λ)y2,

(6)

其中，y3为最终的去噪图像；λ为融合权值，起到平衡偏微分方程和曲波阈值对图像的滤波结果的作用，以达到视觉效果和噪声消除的完美折中，最终收到总体上较满意的去噪效果．

图2 Lena图像

3 仿真实验及分析

图3 基于不同方法得到的去噪图像

噪声方差硬阈值法/dB结构张量PDE法/dB新曲波阈值法/dB文中方法/dB1033.7833.0834.0034.862031.1228.5031.3031.92 3029.4525.2929.5729.61

表2 对Barbara加噪图像的去噪图像PSNR

比较图3(a)与图2(b)可以看出，硬阈值法去噪效果比较明显，图像包含的噪点较少，无明显的色偏现象，图像还原较为真实，但图像有明显的振铃、伪吉布斯效应等视觉失真．比较图3(b)与图3(a)和图2(b)可以看出，软阈值处理后的图像变得模糊不清，并且图像有明显的色偏现象，与原图像有较大差距，并且振铃、伪吉布斯效应等视觉失真依然存在，图像视觉质量较硬阈值法有较大程度的降低．比较图3(d)与图3(a)和图3(b)可以看到，用新阈值函数处理得到的图像与软硬阈值法相比，去噪图像中无肉眼可见的明显噪点，去噪效果较好，而且具有更加丰富的边缘等细节，图像中帽子边缘及帽子上的羽毛纹理都比较清晰，视觉效果最佳．但是，可以察觉到图3(d)与图3(a)和图3(b)同样存在着不同程度丢失帽子边缘及羽毛等重要细节信息的现象，以及3幅图像都出现了许多交错的划痕，即环绕效应．从图3(e)可以看出，噪声残留较图3(c)大幅减少，而图3(c)中图像细节得到较好的保护，但整幅图像存在明显的噪声斑点．图3(e)较图3(d)更加清晰，帽子边缘更加完整清晰，羽毛纹理保护得更好，环绕效应和伪吉布斯效应等视觉失真得到有效抑制，总体视觉效果较好．

由表 1 可以看出 ， 与结构张量 PDE 法去噪图像信噪比相比较 ， 文中提出的新曲波阈值法及其与结构张

量PDE的融合去噪方法产生的去噪图像信噪比有较大幅度提高；与硬阈值法得到的去噪图像信噪比相比，文中提出的新曲波阈值法及其与结构张量PDE的融合去噪方法产生的去噪图像信噪比均有所提高，但提高幅度不大，而前面仿真结果表明，二者均获得了比硬阈值好得多的视觉效果．所以，综合主客观评价指标，可以认为文中方法优于硬阈值去噪法等其他方法．表2再次表明，即使对噪声强度更大、纹理等细节更加丰富的Barbara加噪图像进行去噪，文中方法比其他方法得到的去噪图像信噪比都有较大幅度的提高，去噪效果仍然保持最好．

4 结 束 语

通过对软硬阈值函数在去噪方面优劣的研究，构造了基于卡方累积分布函数的曲波阈值函数，新阈值函数克服了硬阈值不连续和软阈值存在恒定重构误差的缺陷．理论分析和仿真实验一致表明，新阈值函数可以产生更好的去噪效果和视觉质量．进一步地，针对曲波阈值函数固有的环绕效应和难以兼顾去噪与细节保持的弊端，文中采用信息融合的思想，将偏微分方程去噪图像中的有用信息融合到新阈值函数去噪图像中．理论分析和仿真实验一致表明，较软硬阈值去噪法，文中方法可以有效地提高去噪图像的信噪比和视觉效果，较好地保持了图像细节，大幅度降低了环绕效应，具有最优的峰值信噪比和较好的图像适应能力以及优势明显的视觉效果．

[1] Candes E J, Donoho D L. Curvelets: a Surprisingly Effective Nonadaptive Representation for Objects with Edges[M]. Nashville: Vanderbilt University Press, 2000: 105-120.

[2] Candes E J, Demanet L, Donoho D L, et al. Fast Discrete Curvelet Transforms[J]. Multiscal Modeling and Simulation, 2006, 5(3): 861-899.

[3] StarckJ L, Candès E J, Donoho D L.The Curvelet Transform for Image Denoising[J]. IEEE Transactions on Image Processing, 2002, 11(6): 670-684.

[4] Ma J, Plonka G. A Review of Curvelets and Recent Applications[J]. IEEE Signal Processing Magazine, 2010, 27(2): 118-133.

[5] Daubechies I, Defrise M, De Mol C. An Iterative Thresholding Algorithm for Linear Inverse Problems[J]. Communications on Pure & Applied Mathematics, 2004, 57(11): 1413-1457.

[6] Ma Jianwei. Improved Iterative Curvelet Thresholding for Compressed Sensing and Measurement[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(1): 126-136.

[7] Perona P, Malik J. Scale-space and Edge Detection Using Anisotropic Diffusion[J]. IEEE Pattern Analysis and Machine Intelligence, 1990, 12: 629-639.

[8] Brox T, Weickert J, Burgeth B, et al. Nonlinear Structure Tensors[J]. Image and Vision Computing, 2006, 24(1): 41-55.

[9] Ma Jianwei, Gerlind P. Combined Curvelet Shrinkage and Nonlinear Anisotropic Diffusion[J]. IEEE Transactions on Image Processing, 2007, 16(9): 2198-2206.

[10] Weisstein E W. Chi-Squared Distribution[EB/OL]. [2013-08-04]. http://mathworld.wolfram.com/Chi-SquaredDistribution.html.